10MW风力机叶片设计及其在随机风载荷下的响应分析*

倪晨锋，李德源，汪显能，池志强

（广东工业大学机电工程学院，广州 510006）

10MW风力机叶片设计及其在随机风载荷下的响应分析*

倪晨锋，李德源†，汪显能，池志强

（广东工业大学机电工程学院，广州 510006）

对大型风力机柔性叶片的设计方法及其在随机风载荷作用下的动态响应与载荷特性进行了研究。根据风力机叶片空气动力学和结构设计理论，将柔性叶片离散为多个刚体，形成一个多体系统。根据多体动力学的建模方法和叶片气动模型，考虑两者的相互作用，建立了柔性叶片的非线性耦合动力学方程并开发了相应的仿真程序。算例分析了叶片在随机风载荷作用下的气弹载荷与随机振动响应，并对稳定风速和紊流风速下的响应结果作了对比分析。

风力机叶片；超级单元；叶素动量理论；时域响应

0　 引 言

目前10 MW的巨型风电机组已成为风力机领域竞相研发的对象［1］。由于叶片一端与轮毂相连，为类似悬臂梁的细长结构，随着单机功率的增加，叶片愈加细长，柔性和变形越来越大，变形和气动载荷的耦合以及所引起的风电机组气动弹性问题将更加突出。

柔性叶片动力响应分析的困难在于，一方面叶片较大的弹性变形和机械振动会反作用于叶片的空气动力载荷，引起气弹耦合；另一方面风载荷是一个随机变量。响应分析涉及到气动载荷模型和结构动力模型。在气动模型方面，叶素动量理论（blade element momentum， BEM）计算效率较高且结果比较符合实际，在风力机设计领域得到了广泛应用［2］；而对于风力机叶片这类具有较大弹性变形和大范围空间运动构件的动力学建模，应用传统有限元数值进行叶片的气弹耦合计算还有一定困难。ZHAO［3］及 HOLIERHOEK［4］等引入“超级单元”（super-element）将风力机叶片离散为若干个通过运动副、弹簧和阻尼器联接的刚体，通过多体动力学理论可以用较少的自由度建立系统的非线性动力学方程。文献［5］运用多体系统动力学的建模方法，建立了某5 MW风力机整机的刚-柔多体气弹耦合方程，对整机的振动模态和气弹耦合响应进行了数值模拟。

本文针对文献［1］提出的10 MW概念型风力机叶片，应用“超级单元”模型，将叶片离散为6个超级单元，基于多体系统动力学理论，结合叶素动量理论，通过在翼型的入流角和攻角中引入叶片的变形与振动来修正，建立叶片气弹耦合方程，应用Matlab编制动力学方程程序化的建模程序和数值求解程序，得出在稳定风速和紊流风速下的气弹耦合响应。为叶片结构和气动性能的进一步优化设计提供有效的分析手段。

1　 叶片的气动外形设计和结构设计

文献［1］风电机组是一台三叶片、上风向的水平轴风电机组，采用变速变桨控制。额定风速取11.4 m/s，材料为玻璃钢。

1.1叶片的气动外形设计

风载荷作用在风轮叶片上，推动风轮转动，将机械能转化为电能。而叶片所受气动载荷的大小主要决定于叶片的外形，所以叶片气动设计主要是外形的设计。内容主要包括翼型的选择，以及弦长、扭角分布的确定。

设计叶片外形时，气动性能的分析通常采用叶素动量理论，同时考虑多种影响因素，如叶尖和轮毂损失修正、攻角的修正，并考虑气流沿叶片轴向的流动，对轴向诱导因子的修正，建立风电机组气动设计数学模型，综合考虑机组的功率系数，设计完成的叶片弦长和扭角分布。

由于叶片截面翼型直接决定了气动载荷的大小，因此翼型的选择至关重要。考虑到叶根部分与轮毂连接的结构要求，以及叶片气动载荷主要集中在中部到叶尖部分，所以，选择了具有一定尾缘厚度的 FFA-W 系列翼型，分别是 FFA-W3-241、FFA-W3-301、 FFA-W3-360、 FFA-W3-480 和FFA-W3-600，最大相对厚度分别为24.1%、30.1%、36%、48%和60%，靠近叶尖部分选择了最大相对厚度为24.1%。最终得到叶片全长为86.366 m，叶片截面弦长、扭角和厚度随r（r表示叶片的截面到叶根距离）的分布情况分别如图1、图2和图3所示［1］。

图1　弦长随r分布情况Fig. 1 The distribution of the chord along with r

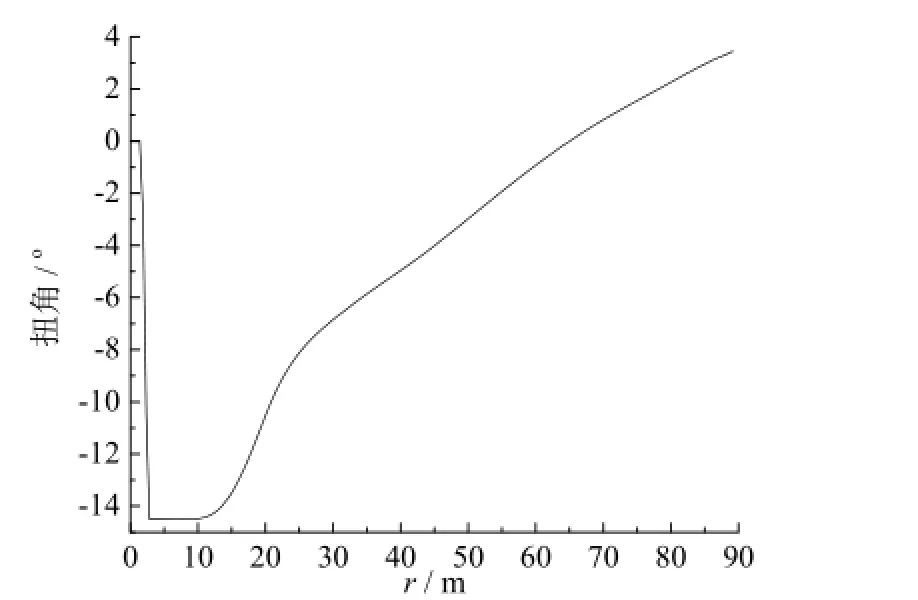
图2　扭角随r分布情况Fig. 2 The distribution of the twist along with r

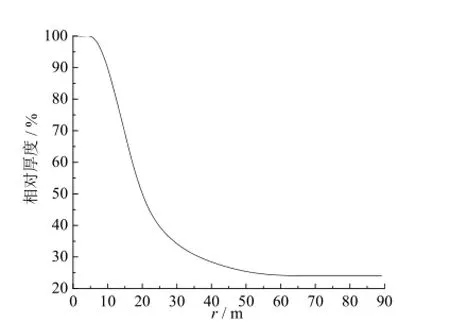
图3　厚度随r分布情况Fig. 3 The distribution of the thickness along with r

1.2复合材料叶片的内部结构设计

复合材料叶片的结构从作用上可以分为蒙皮和主梁两个部分。蒙皮形成叶片外形，同时承受部分气动与机械载荷（如重力等）。主梁是主要的承载构件，通常由梁帽和腹板组成，梁帽承担气动和机械载荷引起的弯曲载荷，腹板置于梁帽空腔内，支撑梁帽，以提高刚度，防止结构屈曲，梁帽一般采用单向布制作，而腹板采用夹层结构制作。叶片的大部分重量集中在主梁上。

文献［1］的叶片铺层中，梁的结构采用了矩形梁形式，复合材料采用了玻璃钢材料。叶片总质量为41 716 kg，结构阻尼比为3%。叶片质量和截面刚度随r的分布情况分别如图4、图5所示。

图4　刚体质量随r分布情况Fig. 4 The mass of the rigid body along with r

图5　刚体截面刚度随r分布情况Fig. 5 The sectional stiffness of the rigid body along with r

2　 柔性叶片多体动力学模型的建立

将柔性叶片离散为若干具有一定质量与形状的体，刚体之间用万向节、转动副和约束力元连接，形成一个多体系统。

2.1叶片的多体模型

将叶片离散为6个超级单元来建立柔性叶片的拓扑模型。每个超级单元包含4个刚体，前后两个超级单元相连的两个刚体刚性连接（即将前一个超级单元的最后一个刚体与后一个超级单元的第一个刚体相连接），合并为一个刚体，形成19个刚体，总共31个自由度的多体系统［5］。

2.2模型中刚体的质量分布与弹簧刚度系数的确定

根据叶片质量分布图（图4），结合超级单元模型中刚体长度，可以提取划分的各刚体质量，如表1所示。弹簧的刚度系数可以通过把叶片简化成悬臂梁模型来确定，如果一个超级单元的长度为L，则刚体B1和B4长为kL，k（k ＜ 1）为长度系数，刚体B2和B3长为（1 - 2kL）/2。根据弹性梁的弯曲及扭转理论，计算出弹簧的刚度系数［3］，计算表达式如下：

式中：E为弹性模量，G为剪切模量，I为截面惯性矩，1xC 为扭转弹簧刚度系数，其余为弯曲弹簧刚度系数。由于长度系数k会对固有频率的近似解产生影响，根据RAUH［6］的结论：长度系数为1/5 ≤ k ≤ 1/4时，则可用较少的超级单元来逼近固有频率精确解，本文取k为0.217 6。根据式（1）～ 式（5）和叶片的截面数据（表 1）得到叶片上各刚体之间的弹簧刚度系数如表2。

表1　叶片截面属性Table 1 Data of the blade section

表2　叶片弹簧刚度系数 / （N·m/rad）Table 2 Spring stiffness coefficients of the blade / （N·m/rad）

根据以上参数，在动力学分析软件adams中建立叶片多体模型，在 adams/vibration振动分析模块中进行模态计算，得到前六阶振型及其对应的固有频率，其结果与DTU实验室［1］提供的结果基本吻合，验证了超级单元方法建模的正确性。

叶片在极端载荷作用下的强度分析工作已经在文献［1］中完成，验证了该叶片静强度和刚度。

2.3带约束的叶片多体动力学方程及其数值求解

由上所述，离散的叶片多体系统由多个刚体通过运动副连接，取各运动副的相对运动为广义坐标θ（t），则由此多刚体系统的树结构形式可得系统的广义坐标矩阵为：

根据多体系统动力学普遍方程，可以导出叶片系统的非线性动力学微分方程组：θ为加速度列阵，推导过程与表达形式可参阅文献［13］。叶片在额定转速下转动，确定的转速相当于运动约束，表达为一代数方程，引入拉格朗日乘子λ，结合方程（7），构成系统封闭的微分-代数方程组。采用违约稳定法处理，采用数值积分可以求出广义加速度

3　 叶片气动载荷分析

作用在叶片上的空气动力载荷分析，一般根据叶素动量理论，但是，由于叶片的变形和振动（挥舞、摆振和扭转振动）反过来会影响气动载荷，考虑流固耦合，本文对传统的气动理论分析迭代过程进行了修正。

叶素动量理论

传统的叶素动量理论通过引入轴向和切向诱导因子，综合考虑了气流的三维流动效应，比较准确地表达了作用在叶片上的气动载荷，在风力机领域应用广泛。计算流固耦合，本文通过在翼型的入流角和攻角中引入叶片的变形与振动来修正模型，使模型更加完善。

叶素理论没有考虑气流的展向流动，将构成叶片展向的多个叶素看成相互独立的二维翼型。风轮绕转动中心旋转一周受到的推力T及转矩Q为：

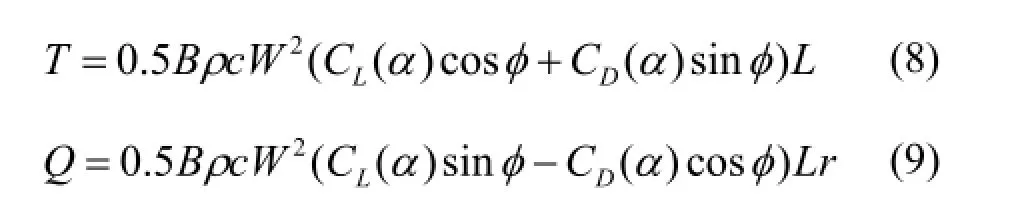
其中：B为叶片数；c是翼型弦长；ρ为空气密度；W是微段dr的转速rω（ω为叶片转动角速度）与来流风速∞U 的合速度；LC 、DC 分别是升力、阻力，随攻角α的变化而变；L为刚体沿叶片径向的长度；r为翼型截面距离轮毂中心的距离；φ为入流角。

而动量理论通过引入轴向诱导因子a和切向诱导因子a′来模拟气流的展向流动，同时考虑叶尖与轮毂涡处复杂的流动，推力和转矩分别表达为：

其中，F为综合考虑叶尖损失和轮毂损失的修正因子。各气动参数对叶素产生气动载荷的作用机理如下图所示。由前面叶素理论的公式可知，确定入流角即可得到叶素上的气动力。

考虑气弹耦合，叶片变形和振动对气动载荷的影响体现在对入流角φ及攻角α的影响上，修正的计算公式为：

其中，θ为各刚体的扭转角；opeV-为翼型垂直于旋转平面（挥舞）速度；ipeV-为翼型平行于旋转平面（摆振）速度。由上述式（8）～式（13），参考DTU实验室［1］提供的二维翼型升阻数据，通过迭代即可算出各气动参数。

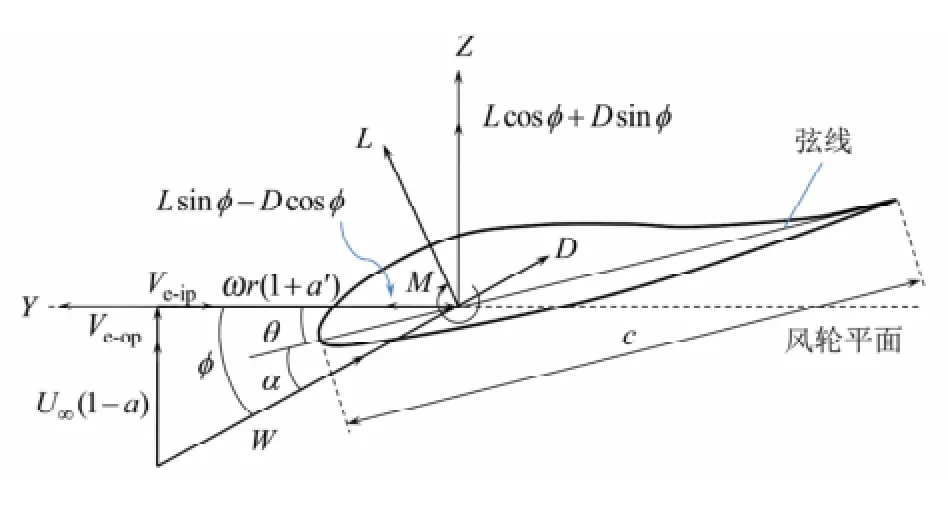
图6　刚体质心截面上的气动参数及气动中心连体基Fig. 6 Aerodynamic variables of center-mass section and body-fixed coordinate system of aerodynamic center of rigid body

4　 叶片的随机风载荷响应分析

气弹耦合仿真首先在求解动力学微分方程的过程中，调入气动模块算出该时刻的气动载荷，将其反馈到动力学模块中，分析得出下一时刻刚体的运动参数并再代入气动模块中，从而可计算出下一时间步的气动载荷，如此循环下去，最后达到设定的仿真时间后结束。气弹耦合分析流程图参考文献［7］。

分析中，叶片以恒定的转速绕轮毂中心转动，这样建立约束方程限制叶片转速：

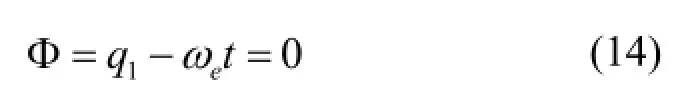
其中，广义坐标q1为叶根刚体相对于风轮转动中心线的转动；ωe为额定转速，9.6 r/min［1］。取α=β=10，仿真时间为50 s，积分精度为0.000 1，输出积分步长0.001 s。

以仿真分析了设计的10 MW叶片在稳定风速和紊流风速下（这里风速为11.4 m/s）叶片扭转变形和振动对气动载荷的影响。对比了两种风速下，叶尖的位移和叶根的位移以及各刚体的攻角变化对气动载荷的影响。

图7是在稳定风速和紊流风速下叶片第1个刚体（叶根位置）位移随时间的变化曲线。图8是在稳定和紊流风速下第19个刚体（叶尖位置）力矩随时间的变化情况。从叶尖位移变化图可以看出，在叶片进入稳定运行后，稳定风速下叶尖挥舞位移按照一定的周期变化，位移范围在6.3 ～ 7.3 m；而紊流风速下叶尖挥舞位移变化没有规律波动较大，变化范围4.9 ～ 8.1 m。这两种风速下叶尖的最大位移都没有超过叶片与塔架的距离18.26 m［1］（防止叶片在运行过程中与塔架相撞）。

图7　第1个刚体挥舞与摆振力矩Fig. 7 The flapwise and edgewise bending moment of the first rigid body

图8 第19个刚体挥舞与摆振方向位移Fig. 8 The flapwise and edgewise displacement of the 19th rigid body

图9是在稳定和紊流风速下某一截面攻角随时间的变化情况。可以看到，在叶片运行稳定后，稳定风速条件下攻角的波动比紊流风速下攻角的波动要小，对气动力的影响也会更小。

图9　某一截面攻角随时间的变化情况Fig. 9 The curves of time versus varying angle of attack of a cross-section

从叶根力矩图（图 7）同样可以看到，在稳定风速下的叶根力矩的波动比紊流风速下的叶根力矩要小，具体的对比结果如下表 3。由于在两种不同的风速下，叶片的扭转速度和扭转变形不同，导致攻角有很大的差异，使得气动载荷也不相同，当然最终得到的叶根力矩也会有很大的差别。因此，对于大型风力机，需要考虑叶片的振动和扭转对气动载荷的耦合。

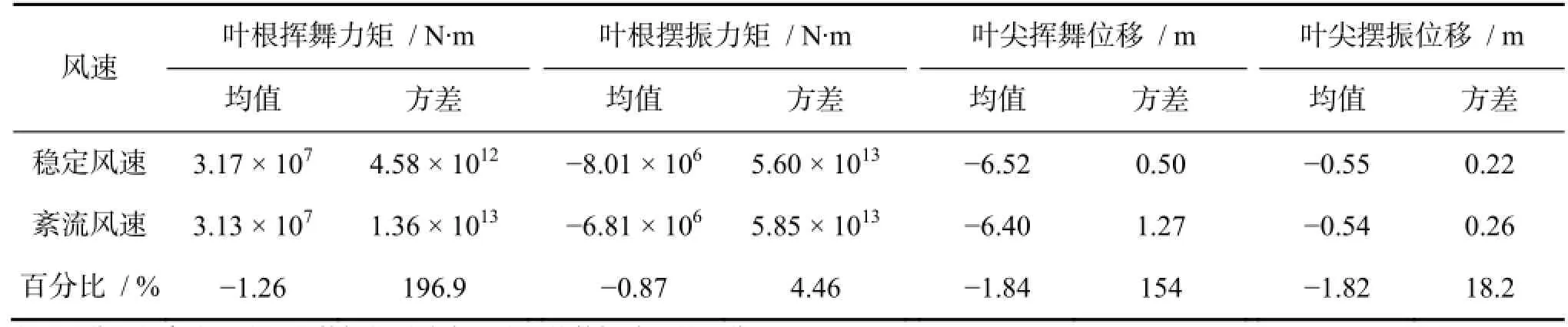
表3　两种风速下的数据对比Table 3 The contrast of the data in the two kinds of wind

5　 结 论

（1）在综合考虑风力机的气动性能与结构强度基础上，设计了10 MW风力机叶片的气动外形和内部结构。建立了柔性叶片的多刚体动力学模型，结合多体动力学建模方法和风力机气动分析模型，构建了柔性叶片非线性流固耦合方程，并开发了相应的数值分析软件，能够分析在随机风速作用下，实现在叶片实时变形位置分析叶片的气动载荷，并获得叶片的动力学响应情况。

（2）分析两种风况条件下叶片的振动响应和气动载荷，并进行了对比分析，结果表明所设计的叶片满足设计要求。采用所提出的叶片气弹耦合分析方法，能够较为有效地展现叶片的振动与气动载荷之间的耦合关系。

［1］ BAK C， ZAHLE F， BITSCHE R， et al. Description of the DTU 10MW reference wind turbine［R］. DTU Wind Energy Report-I-0092， 2013.

［2］ HANSEN M O L， SØRENSEN J N， VOUTSINAS S， et al. State of the art in wind turbine aerodynamics and aeroelasticity［J］. Progress in aerospace sciences， 2006，42（4）: 285-330. DOI: 10.1016/j.paerosci.2006.10.002.

［3］ ZHAO X Y， MAIßER P， WU J Y. A new multibody modelling methodology for wind turbine structures using a cardanic joint beam element［J］. Renewable energy，2007， 32（3）: 532-546. DOI: 10.1016/j.renene.2006.04.010.

［4］ HOLIERHOEK J G. Aeroelasticity of large wind turbines［D］. Delft: Delft University of Technology， 2008.

［5］ 李德源， 莫文威， 严修红， 等. 基于多体模型的水平轴风力机气弹耦合分析［J］. 机械工程学报， 2014， 50（12）: 140-150. DOI: 10.3901/JME.2014.12.140.

［6］ RAUH J， SCHIEHLEN W. Various approaches for the modeling of flexible robot arms［C］. Proceedings of the Euromech-Colloquium 219 on Refined Dynamical Theories of Beams， Plates and Shells and Their Applications. Berlin Heidelberg: Springer， 1987: 420-429. DOI: 10.1007/978-3-642-83040-2_36.

［7］ 李德源， 莫文威， 夏鸿建， 等. 水平轴风力机柔性叶片气弹耦合分析［J］. 太阳能学报， 2015， 36（3）: 734-742.

［8］ HANSEN M O L. Aerodynamics of wind turbines［M］. 2nd ed. Denmark: Routledge， 2007.

［9］ HOLIERHOEK J G. Rigid body modeling of wind turbines for aeroelastic stability investigations［C］//45th AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada: American Institute of Aeronautics and Astronautics Inc， 2007: 2485-2497. DOI: 10.2514/6.2007-210.

［10］ LI L， LI Y H， LIU Q K， et al. Flapwise non-linear dynamics of wind turbine blades with both external and internal resonances［J］. International journal of non-linear mechanics， 2014， 61: 1-14. DOI: 10.1016/j.ijnonlinmec. 2014.01.006.

［11］ COX K， ECHTERMEYER A. Structural design and analysis of a 10MW wind turbine blade［J］. Energy procedia， 2012， 24: 194-201. DOI: 10.1016/j.egypro. 2012.06.101.

［12］ 齐朝晖. 多体系统动力学［M］. 北京: 科学出版社，2008.

［13］ 洪嘉振. 计算多体系统动力学［M］. 北京: 高等教育出版社， 1999.

Design of the10 MW Wind Turbine Blade and Its Response Analysis under Random Wind Loads

NI Chen-feng， LI De-yuan， WANG Xian-neng， CHI Zhi-qiang
（School of Electromechanical Engineering， Guangdong University of Technology， Guangzhou 510006， China）

This paper presented a design method of the flexible blade and its dynamic response under random wind. The flexible blade was discretized into multiple rigid bodies， and the multi-body system was established according to the theory of aerodynamics and the structural design of the blade. The nonlinear aeroelastic coupling equations of a constrained flexible blade are derived by the dynamics of multi-body system theory and the blade aerodynamics model， and the simulation program was developed. The examples analyzed time-domain responses of the blade under stable and turbulent wind speed， and the results were compared under these two kinds of wind speed.

wind turbine blade； super-element； blade element momentum； time-domain response

李德源（1965-），男，教授，硕士生导师，主要从事大型风力机气动与结构分析、风力机系统测试和计算机软件的开发与应用等方面的科研工作。

TK83

A

10.3969/j.issn.2095-560X.2016.03.007

2095-560X（2016）03-0206-07

2016-03-03

2016-04-17

国家自然科学基金项目（51276043）

倪晨锋（1991-），男，硕士研究生，主要从事风力机气弹耦合研究及风力机结构设计。