小学数学教学中数形结合思想的渗透策略
2016-08-12陈向锦长乐师范学校附属小学福建长乐350200
陈向锦(长乐师范学校附属小学,福建 长乐 350200)
小学数学教学中数形结合思想的渗透策略
陈向锦
(长乐师范学校附属小学,福建 长乐350200)
“数形结合”是一种重要的数学思想方法。本文从认识概念、理解算理、探寻关系、揭示规律等方面阐述在课堂教学中如何渗透数形结合思想,以期落实课程标准提出的多维数学教育目标的要求,提升学生的思维品质,形成良好的数学素养。
数形结合;认识概念;理解算理;数量关系;揭示规律
数形结合就是通过数和形之间的对应关系和相互转化来解决问题的思想方法。它作为一种重要的数学思想,既有鲜明的数学学科特点,又是一种数学方法,更是后续学习函数、解析几何等知识的思维基石。小学生思维特点是从形象思维逐步向抽象思维过渡,小学阶段数形结合重点研究的是“以形助数”。在日常课堂教学中,教师如何以形的直观为依托,帮助学生丰富表象,渗透数形结合思想呢?下面结合具体实践谈谈笔者的做法。
一、借助感性图示,形象诠释概念
数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式,往往是很精炼的、高度抽象的。这与正处在小学阶段的学生知识经验不足,形象性为主的思维特征形成鲜明的对比。如果能提供丰富的感性材料,借助直观手段将数学概念中最本质的属性,通过恰当的形式表现出来,将数与形有机整合,让学生在头脑中对概念有直观的印象,就可为建构数学概念奠定基础。

教师先出示图一,引导学生比较胡萝卜和白萝卜的根数,发现两者数量间的相差关系和倍数关系。再向问题:怎样才能让人一眼看出白萝卜是胡萝卜的几倍?引发学生思考。在动手操作后,明白把2根看作一份,白萝卜有3个2根,所以白萝卜的根数是胡萝卜的3倍。学生通过动手摆放、画圈,加以有条理的复述,清晰地理解“白萝卜的根数是胡萝卜的3倍”的具体含义。继而,提问学生:如果白萝卜的根数是胡萝卜的4倍、5倍……你会摆出白萝卜的数量吗?学生通过具体、直观的操作,明白“几个2就是2的几倍”,进而抽象出“几个几就是几的几倍”。学生初步建立起“1份”为标准的意识,知道当比较量出现变化时,就会引起两种量之间的倍数关系。而当“1份”的量出现变化时,比的标准改变了,两种量之间的倍数关系也就变了。学生通过整体对比,充分感受“比”的标准的重要性,有效建构“倍”的概念。
这样,从演示图形到让学生动手摆圈,学生看到了“个数”和“份数”,最后引出“倍数”,概念的呈现有了丰富的图形承载,学生既能体会到前后知识的衔接,又能触及到概念的本质。
二、借助图像表征,直观理解算理
算理就是计算方法的道理,是计算方法的源头与依托。但算理又是抽象的,而数形结合借助图形直观性的特征,成为理解算理的一种有效策略。
如在教学《两位数乘两位数》时,由于学生仍处于直观形象思维阶段,在两位数乘两位数竖式建模及计算方法的梳理描述时较为困难,而借助几何直观帮助学生理解抽象的算理、总结算法就显得至关重要。学生在已有两位数乘一位数的基础上,自主尝试用口算解决问题。

生1:12×14=168生2:14×12=168
12×10=12014×10=140
12×4=482×14=28
120+48=168140+28=168
2.1 家系Ⅰ 检出致病基因为MYO7A基因的c.397dupC和c.4937C>A两个位点复合杂合突变;患者(Ⅱ1、Ⅱ2)视力、视野检查表现为视野周边环形缺损,视野,视力下降;眼底检查:视盘蜡黄色改变且有萎缩,视网膜血管狭窄成青灰色线样,视网膜色素沉着赤道部,诊断为Usher综合征Ⅰ型。MYO7A基因c.397dupC位点突变为国内首报新突变位点,结果、家系图及测序突变。见表1、表2、图1、图2。
教师出示点子图,让学生在图中依次圈出各算式所表示的部分,说说这样算的道理,引导学生在对比基础上得出先分后合的相同点(都是拆分成几个几和几十个几),在此基础上引导学生用竖式计算,由数到图再到数的过程中,结合几个重点问题捋清算理.

最后引导学生给四个乘法算式(2×4=8,1×2=2,1× 4=4,1×1=1)在点子图中找相应的位置,帮助学生掌握积的定位,明白数位对齐的道理。此环节中,点子图给两位数乘两位数的算理呈现提供了具体载体,让算理看得见,摸得着,真正实现以理驭法,理法并重。
小学教学中还可以利用长方形模型来教学分数乘以分数的算理,用线段图来帮助学生理解分数除法算理,利用面积模型来解释乘法分配律、完全平方式等。
三、借助几何直观,清楚凸显关系
解决问题离不开对问题进行有效分析,引导学生从多角度、多侧面分析问题,借助实物图、示意图、线段图等直观图形能更好地帮助学生理清数量间的关系,有效降低学生解决问题的难度。
如五年级下册教材在学生学习了异分母分数加减法后安排了《解决问题》一课:一杯牛奶,乐乐喝了半杯后,觉得有些凉,就兑满了热水,又喝了半杯,就出去玩了。他一共喝了多少杯纯牛奶?多少杯水?由于学生未学习分数乘法的意义,这里的第二次喝半杯,喝的是几杯纯牛奶,就是理解与解决问题的关键,也是难点。教学中,先让学生分析理解题意,在演示喝牛奶的场景后,让学生说:同样都是,喝的牛奶一样吗?你能借助图形表示出来吗?同桌合作、交流后,学生呈现自己的思路。
学生共同表述第二次杯与整杯纯牛奶之间的关系。这里,借助数形结合有效地展现问题本质,有利于帮助学生直观理解数学,通过观察,推理,发现数量之间的关系,有利于学生体验数学创造的历程,调动学生主动参与教学过程并积极思考,培养学生的能力。以上课例采用有效生活情境来进行教学设计,着重利用直观几何图形来解决实际问题,使量与率之间的对应关系一目了然,学生能轻松解决问题。
四、借助图表交互,巧妙揭示规律
数学广角知识重在渗透数学思想,巧妙借助图表、图例等将思维过程呈现出来,以凸显内在规律,在建构知识的同时还可帮助学生积累数学活动经验,发展思维。
如五年级下册《找次品》,在学生分组操作、交流中得出结论:9瓶口香糖中有一瓶是次品,保证能找到次品,用天平秤(3,3,3)时,需要的次数最少,只要秤两次即可找到次品,后教师引导学生“回头看”,借助图表梳理思路:
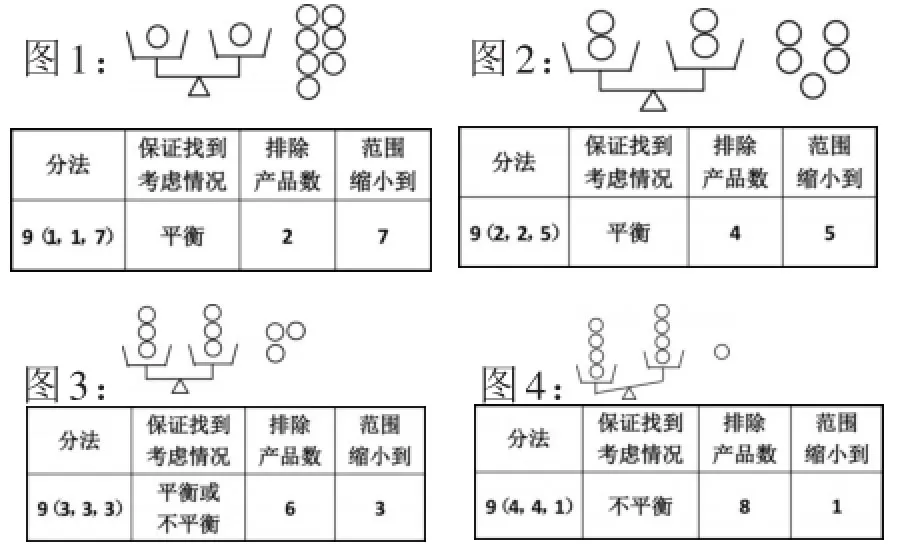
此时学生的思维在直观图表的刺激下,诱发了精彩发言——三个数之间越接近,也就是排除的数量越多,缩小到的范围也就越小。一下子拨开云雾见天日,找次品三等分的奥秘就呼之欲出了。
正是有了学生之前充分的操作、体验、交流、思维碰撞,学生积累了丰富的感知经验。但如果仅仅停留在操作层面,学生仍然无法触摸到思维的本质。“回头看”这一环节,借助图表引导学生反思,在具体的图表这一“形”的“烘托”中,学生自主发现利用天平找次品要“三等分”,并且理解为什么要“等分”,真正达到“知其然,且知其所以然”。思维外显,是一件非常困难的事,但数形结合却以其独特魅力达到这一目的。
[1]教育部.义务教育数学课程标准(2011版)[S].北京:北京师范大学出版社,2012.
[2]钟建林,林武.小学数学专题式教学导引[M].福州:福建人民出版社,2012.
[3]王永春.小学数学与数学思想方法[M].上海:华东师范大学出版社,2014.
(责任编辑:陈志华)
本文系教育部福建师范大学基础教育课程研究中心2014年度开放性课题(项目编号:KCX2014012)研究成果。
