引导多维质疑 培养提问能力

黄平平（长汀县实验小学，福建 长汀　366300）



引导多维质疑 培养提问能力

黄平平
（长汀县实验小学，福建 长汀366300）

提出问题的能力、是学生在数学学习中要培养的一种重要素养。在课堂教学中教师要千方百计引导学生，让学生学会在理解的疑难处和认知的矛盾点上提出数学问题；学会从看似没有疑问的知识中发现问题、提出问题；学会从不同的角度发现问题、提出问题；学会运用比较法从知识的相同之处或不同之处发现问题、提出问题。不断积累丰富的提问经验，做到想问、敢问、会问、善问，最终实现提问能力上质的飞跃。

发现问题；提出问题；能力

在数学课堂教学中教师要努力通过各种方法和途径，引导学生多维发现问题，主动提出问题。为学生的后继探究问题和解决问题夯实基础。从而实现让学生顺利从发现问题→提出问题→探究问题→解决问题过渡，最终为培养学生“问题解决”的能力做充分准备。

一、遇疑就问，学会疑难处提出问题

学起于思，思起于疑。学生的学习过程，常会遇到难以理解或与自身原有的认知结构相冲突的疑难。在教学中应不失时机地引导学生在理解的疑难点或在认知的矛盾点上生发问题并提出来，养成遇疑就问的良好习惯。

1.在理解的疑难处提问

理解的疑难处因学生个体的认知水平而异。可能是知识本身的疑难点，也可能是学生知识基础差而形成的非知识本身的疑难点。这些疑难点都是提出问题的触发点，应引导学生遇理解的疑难处就提出相应问题。例如：学习推理填数时（见图1），可引导学生自己把遇到的疑难点提出来。如：那么多空格应该先填哪一格呢？字母A有什么作用呢？在学生主动提出问题并进行思考、讨论后，处于充分疑惑渴求解决情境之中时再出示小精灵的提示。学生不难发现A与B不同点在于A所在空格的行与列出现了三个不同的数，只要先找出A是多少（用排除法找出A是4），随后用同样方法不难找出B是1。思路大开的学生很快找出第一列和第二行所缺的数分别是2和3。到了这一步，新的疑难点又出现了（见图2）。有些空格所在的行和列只出现了两个不同的数，在学生愁眉不展时可激励学生说出自己遇到的问题。如：怎么选择先填哪个空格？空格所在的行和列只出现了两个不同的数，能确定空格应填几吗？如何确定呢？……通过新旧问题的对比学生就能举一反三，更能触类旁通解决类似的其他问题。只要在数学课堂上持之以恒地这样引导，学生就能养成遇疑就问的习惯。从而逐渐善于在疑难处从数学角度不断提出有效的问题，不断探究、解决数学问题。同时也不断提高“生发问题”和“问题解决”的意识。

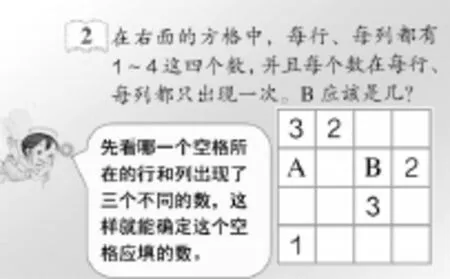
图1

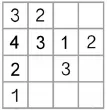
图2

2.在认知的矛盾点提问

“认知矛盾”是学生学习新知的有效动力。学生的新知学习和建构都是新旧认知不断反复矛盾到统一的过程。当学生所学的新知识与原有的认知结构不相符合时，两者必定会产生矛盾冲突，矛盾冲突自然产生问题。故而教学中应择机有效引导学生抓住自己认知的矛盾冲突点提出数学问题。例如，学习分数加减法计算方法时，学生受原有的认知结构中“相同数位上的数分别相加减”的整数、小数加减法的计算方法的影响，往往认为要把分数的分子、分母分别相加减——他们把分子与分子、分母与分母分别当成相同数位的数，而想把其计算方法纳入原有认知结构中，此时，两者产生矛盾冲突，应及时抓住这个矛盾冲突点引导学生提出问题。例如：同分母分数加减法为什么分子可以相加减而分母不能相加减？如果把分母相加减结果会怎样？为什么异分母分数加减法分子、分母都不能直接相加减呢？……这样，学生就学会在认知的矛盾点上提出问题，同时又让学生在矛盾中统一新旧认知的共同点是必须“相同单位”的数才能相加减，也统一认识掌握了同分母分数相加减是分母不变，分子相加减；异分母分数相加减必须先化成大小不变的同分母分数，再按同分母分数加减法则进行计算。这样长期坚持能教会学生善于在认知矛盾点提出数学问题，并进一步去探究、解决问题。

二、无中生有，学会无疑处提出问题

宋代教育家朱熹说：“读书无疑者，须教有疑，有疑者却要无疑，到这里方是长进”。［1］因此，教学中应引导学生学会从看似没有疑问的知识中不断发现新的问题、不断提出新问题。从而增强学生思维的积极主动性、全面性和完整性。例如：教学长方体的认识后，学生认为对长方体的特征都已掌握，似乎没有什么问题。教师仍应引导学生提出新的问题并验证新问题，如：有六个面的物体一定是长方体吗？（不一定）长方体有没有相对的面面积不相等的？（没有）长方体的十二条棱有没有可能都相等？（没有，只有特殊的长方体即正方体才12条棱都相等）长方体的六个面有可能都相等吗？（没有，只有特殊的长方体即正方体6个面都相等）长方体的相邻的3个面或3条棱有可能相等吗？（不可能。否则变正方体了）……这一系列新问题的提出和验证，让学生积累从无疑处不断发现新问题、提出新问题、解决新问题的经验。同时使学生的数学思维能力和学习能力得到全面的发展。

三、变换角度，学会多侧面提出问题

教师在教学中应激励学生从知识的不同角度发现问题、提出问题，培养逆向、发散等思维能力。

1.侧向提问

从知识的某一个侧面入手提出问题。例如，学习了三角形面积计算后，可引导学生提出：用三角形侧边（或斜边）长乘该边上的高再除以2，能不能求出三角形的面积？用三角形不同边的长乘对应的高除以2计算出的结果是否相等？然后引导学生对自己提出的问题加以验证，自行比较分析，得出结论。这样不但使学生深刻理解了三角形面积（同样用公式S=ah÷2）计算方法的多样化，而且使学生经历了从另一侧面（另一角度）提出问题的活动过程，有效积累了相关活动经验。

2.逆向提问

从知识规律相反的方向提出问题。例如，学习了用“看大数、拆小数、凑满十”的方法来计算20以内的进位加法后，可引导学生逆向思考提出问题：可不可以用“看小数、拆大数”的方法来凑十呢？（可以。例如6+ 9=？可先想把9拆成4和5，6和4凑成10，再想10+5= 15）。让学生有效积累逆向提问的活动经验。充分有效激活学生正反“互通”的数学思维方式。让学生的“生发问题”和“问题解决”能力得以全方位的拓展。

四、运用比较，学会异同处提出问题

乌申斯基说：“比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切的”。［2］比较是学生建构知识过程中必备的环节。因此，教学中引导学生运用比较法从知识的相同之处或不同之处发现问题、提出问题，不仅能深化认知、还能有效发展其发现问题、提出问题和解决问题的能力。

1.同中求异提问

有些知识本质相同，但表面看来似乎不同。教学中，可根据其同质异象的特点，引导学生用比较法同中求异发现问题、提出问题。例如：学习了小数加减法后，可让学生将其计算方法与整数加减法计算方法进行比较，从中提出问题：计算整数加减法和小数加减法都要把相同数位上的数对齐，为什么整数加减法把末位对齐，而小数加减法却要把小数点对齐？小数加减法把末位对齐为什么不可以？［3］这些问题的提出，不仅有助于学生深入理解算理，还能丰富学生从相同事物中发现不同问题的体验。

2.异中求同提问

有些知识本身各不相同，但却隐含着某种联系或共同之处。教学中，可引导学生对不同的知识，产生有没有共同之处的疑问，逐步掌握异中问同的提问方法。例如，长方体、正方体、圆柱体各自常用的体积计算公式因形体特征不同而各不相同，可引导学生观察比较其形体特征和计算公式，产生这些形体的体积能不能用一个相同的计算公式的疑问，从而提出：它们的体积可不可以都用底面积乘高的方法来计算？进而又有学生提出：只要上下底面一样的形体它们的体积是否都可以用底面积乘高来计算？它们的侧面积是否都等于底面周长乘高？（通过验证是可以的）……这些问题的提出，有些虽已超出教学目标要求，却是学生自主发现问题、提出问题、解决问题的体现，对学生积累异中问同的提问经验大有好处。同时，也有助于学生思维的持续性、思维的延伸性、思维的创造性的培养。

［1］陈晓浒.向朱子读书法学读书［M］.南京：凤凰出版社，2014.

［2］张汉文.运用比较 发展思维［J］.天津教育，1993（3）.

［3］李育飞.新课程理念下的课堂教学该注重什么［J］.新一代（下半月），2014（5）.

（责任编辑：陈志华）