在教学中让学生经历知识形成的过程
——“同底数幂的乘法”教学设计
2016-08-12高晓微内蒙古呼和浩特市实验中学杨鲜枝内蒙古呼和浩特市教学研究室
高晓微 田 斌(内蒙古呼和浩特市实验中学)杨鲜枝(内蒙古呼和浩特市教学研究室)
在教学中让学生经历知识形成的过程
——“同底数幂的乘法”教学设计
高晓微田斌(内蒙古呼和浩特市实验中学)
杨鲜枝(内蒙古呼和浩特市教学研究室)
摘要:同底数幂的乘法法则探索过程遵循由特殊到一般的规律.通过教师提供素材,让学生自主探索,发现规律,生成法则,抽象概括出表达式am·an= am+n,法则的形成过程就是学生经历数学活动的过程,积累数学学习经验的过程.
关键词:自主学习;同底数幂;生成法则;特殊到一般;抽象概括
教学内容分析
“同底数幂的乘法”是人教版《义务教育教科书·数学》八年级上册第十四章第一节的内容.同底数幂的乘法是在学生学习了有理数的运算和整式的加减之后,为了学习整式的乘除法而学习的关于幂的一个基本性质.在整式的乘除法中,单项式的乘除是关键,因为其他乘除都要转化为单项式的乘除.而单项式的乘除进行的是幂的运算与有理数的运算,因此幂的运算是学好整式乘除的基石.而同底数幂的乘法又是另外两个性质(幂的乘方和积的乘方)的基础.所以同底数幂的乘法是整式乘法的逻辑起点,是该章的起始课,承载着单元知识、学习方法以及学习路径的引领作用.这节课的学习,重、难点在于学生理解法则的由来,自主归纳、概括法则.只有这样学生才能从本质上体会法则,掌握法则,学会由特殊到一般的归纳过程和方法.
教学重点:同底数幂乘法法则的形成及正确运用.
教学难点:同底数幂乘法法则的形成.
学生学情分析
学生已掌握有理数的运算,并已初步具有用字母表示数的思想,但用字母来归纳同底数幂的乘法法则,使其具有一般性,对学生的抽象思维能力和逻辑推理能力要求较高.因此,教师设计了从特殊到一般的方法,引导学生观察、归纳、发现,并概括出同底数幂的乘法法则.
教学目标设置
(1)让学生经历法则的形成过程,能正确使用同底数幂乘法法则进行计算.
(2)引导学生观察、发现、归纳、概括同底数幂乘法的法则,发展学生的推理能力.
(3)了解生活与数学的相关信息,通过同底数幂乘法法则的探索和应用,学生初步体会由“特殊—一般—特殊”的认知规律,从中获得成功的体验,感受学习数学的乐趣.
教学策略分析
学好同底数幂的乘法的基础是正确理解底数、指数、幂的概念和乘方的意义.教学中要注意联系过去不甚巩固的知识,将新、旧知识有机地融合在一起.从具体的情境中抽象出数量关系,发现同底数幂相乘的运算,使学生体会学习同底数幂的乘法的意义.通过设置环环相扣的“问题串”,引导学生自主学习、合作探究,抽象概括出同底数幂的乘法法则.
教学时要特别注重以下几点:
(1)重视法则的形成过程.
(2)重视用字母表示数的思想.
(3)在探索法则时,遵循由特殊到一般的规律.
教学方法有自主学习、合作探究、引导启发、变式练习.
教学支持条件
借助多媒体课件,呈现形象、直观的实例背景,激发学习兴趣,启迪学生思维.借助实物投影,在法则的探索与运用中让学生充分展示他们的思维过程,亲历知识的发生、发展和形成过程.
教学流程设计
1.创设游戏,复习巩固
师:我们做一个小游戏,比一比看谁算得快!
2×2,2×2×2,2×2×2×2,2×2×2×2×2,…
生:4,8,16,32,64,…
师生互动:
(1)算式2×2×2×2×2×2×2×2×2,还可以将它写成什么形式?
(2)103表示什么?
(3)像29和103我们称之为什么?
(4)说出an中的a,n,an分别叫做什么,它们各表示什么?
【设计意图】设计比一比看谁算得快的小游戏,产生形如2×2×2×2×…多个相同的因数的乘积,复习乘方的意义,巩固幂的概念,为学生认识同底数幂的乘法做下铺垫.本章学习的是整式的乘法,本着数式通性的原则,先复习数的运算,再探究式的运算.
2.创设情境,引出课题
师:像上面那样在数字2的基础上依次乘2这样的计算,你一秒钟能计算多少次?
生1:1次.
生2:2次.
……
师:老师有一个好朋友,它每秒可进行1千万亿(即1015)次运算,你们知道它是谁吗?
生:是计算机吗?
师:是的,相信它也是大家的好朋友.下面我们来看下面这个问题.
问题:一种电子计算机每秒可进行1千万亿(即1015) 次运算,它工作103秒可进行多少次运算?
生3:1015×103.
师:1015×103等于多少?
学生独立计算(教师提示:根据乘方的意义).学生回答,教师板书:
1015×103根据
=乘法的结合律
=1018……(3)根据乘方的意义将乘法转化为幂
【设计意图】创设问题情境,体会信息技术带来的“大数据”时代.由这个问题列出式子1015×103,学生感受到学习同底数幂的乘法的意义.教师在学生回答的过程中引导学生准确说出每一步的解题依据,理解每一步的算理、算法.通过有步骤、有依据的计算为探索同底数幂乘法的运算法则做好知识和方法的铺垫.
3.合作学习,探索法则
(1)提出任务,自主探索.
例如:24×23=(2×2×2×2)×(2×2×2)=2×2× 2×2×2×2×2=_______.
师:我们完成下面的填空(m,n都是正整数):
第一组:
①65·66=_____=______=______.
②a4·a5=_____=______=______.
③m4·m4=______=_____=______.
④5m·5n=_____=______=______.
第二组:
①(-3)5·(-3)6=______=_____=______.
③a300·a200=______=_____=______.
④9.8m·9.8n=_____=_____=______.
学生完成后,用投影展示,引导学生讲出每一步变形的理由,展示他们的思维形成过程.
【设计意图】学生思维的具体性与直观性决定了在数学学习中要给他们提供充分的感性经验,使他们经历数学知识形成的过程,从而更好地形成抽象的数学概念,获得新的数学知识.两组计算每一道题都经历“幂×幂转换为乘法运算再转换到幂的形式表示”的过程,而且底数由整数逐渐变换为分数、负数、字母.指数由较小正整数逐渐变大再变换为字母,学生在经历了由简到繁的运算活动,思维也经历了一个由浅入深、由具体到抽象的活动过程.
(2)细心观察,揭示课题.
师:前面要求计算的这些算式有什么共同特点?生:是两个底数相同的幂相乘.
师:像这样两个底数相同的幂相乘,叫做同底数幂的乘法(板书课题).
【设计意图】学生自己发现这些算式的特点,识别同底数幂的乘法,产生课题.
(3)合作交流,概括法则.
师生互动:①小组讨论上面的算式有什么规律?
②你能用一个式子来表示这个规律吗?
③你能解释为什么am·an=am+n吗?
学生讲解,教师板书如下.

【设计意图】通过学生观察、发现、归纳、概括出同底数幂的乘法法则,抽象概括出表达式am·an=am+n(m,n为正整数),学生在自然生成法则的过程中,体会字母表示数的意义,也体现了数学的模型思想.学生不仅学会了法则,更学会了探究这一类问题的由特殊到一般的方法.
4.运用法则,巩固新知
师:下面我们运用同底数幂乘法法则计算.
计算:1015×103.
变式:1015×103×102.
生4:运用前面的结果1015×103×102=1018×102=1020.
生5:1015×103×102=1015+3+2=1020.;
④x3·x+x2·x2.
(2)辨析填空:①b5·b5=__________;
②b5+b5=_________.
(3)填空:①x2·()=x8;②xm·()=x3m;
③x8=()·();④3×27×9=3·().
(4)卫星绕地球运动的速度是7.9×103m/s,求卫星绕地球运行2×102s走过的路程.
(5)计算:①a2·a(-a)4;②(a-b)·(a-b)3;
③(a-b)·(b-a)4.
【设计意图】通过第(1)小题进一步熟练法则.第(2)小题中相似的算式产生思想冲突,让学生经过“比较”解决冲突,识别同类项与同底数幂相乘.第(3)小题逆向使用法则,培养学生综合分析问题的能力.第(4)小题用所学知识解决简单的实际问题.第(5)小题属于拓展延伸,即底数互为相反数的幂的乘法.
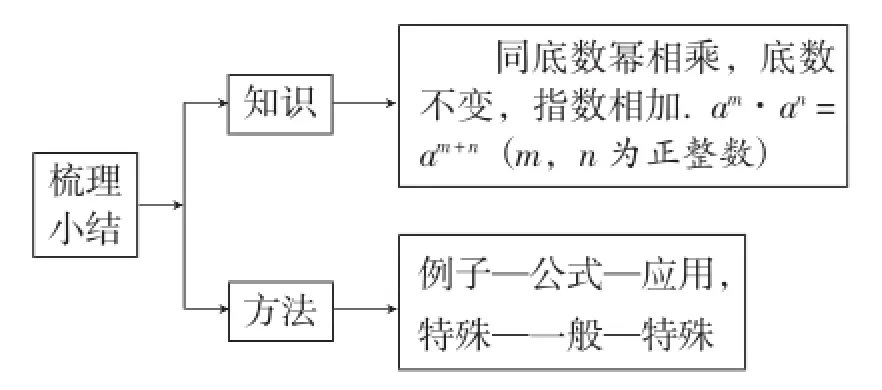
6.梳理小结,知识深化
【设计意图】 对法则进行推广,即am·an·ap=am+n+p(其中m,n,p都是正整数).
例运用法则计算下列各式.
(1)a·a5;
(2)2a·2b;
(3)xn·x3n+1;
(4)(-2)×(-2)4×(-2)3.
思考题:34×43和 a3+a3能不能用同底数幂乘法法则计算?
【设计意图】辨析法则使用的条件,体会将同底数幂乘法运算转化为指数的加法运算的思想.
5.目标检测,拓展延伸
(1)计算.
①a2·a6;
②y2n·yn+1;
③
变式计算:27·210可一般化为a7·a10.
若底数为a-b,则可变式为(a-b)7·(a-b)10;
若底数为ab,则可变式为(ab)7·(ab)10;
若底数为a3,则可变式为(a3)7·(a3)10.
【设计意图】引导学生从知识和方法两个角度做总结,渗透“特殊—一般—特殊”的思想方法和转化的思想.通过将底数进行变形,变成积的形式,幂的形式得到:(ab)17,(a3)17(不要求进一步化简),为后面的学习埋下伏笔,将本节知识延伸,使其置于数学整体知识体系当中.
作业:教材第96页练习,第105页第10题.
参考文献:
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]人民教育出版社课程教材研究所中学数学课程教材研发中心.义务教育教科书·数学(八年级上册)[M].北京:人民教育出版社,2013.
[3]人民教育出版社课程教材研究所中学数学课程教材研发中心.《义务教育教科书·数学》教师教学用书(八年级上册)[M].北京:人民教育出版社,2013.
[4]赵维坤.在数学实验中发展学生的推理能力[J].中国数学教育(初中版),2015(11):27-31.
[5]周莹,唐剑岚.将探究融入教学活动中[J].初中数学课例点评,2008(9):45-50.
收稿日期:2015—12—26
作者简介:高晓微(1983—),女,中学二级教师,主要从事初中数学教学研究.
