基于单循环功能度量法的结构可靠寿命优化设计

刘　勤，孙志礼，涂宏茂，姬广振

(1.东北大学 机械工程与自动化学院，沈阳　110819； 2.中国兵器科学研究院，北京　100089)



基于单循环功能度量法的结构可靠寿命优化设计

刘勤1,2，孙志礼1，涂宏茂1,2，姬广振2

(1.东北大学 机械工程与自动化学院，沈阳110819； 2.中国兵器科学研究院，北京100089)

摘要：针对常规的寿命优化设计，未考虑疲劳、磨损影响系数等因素的分散性，引入单循环方法，提出了一种以可靠寿命为目标、约束的结构优化设计方法；将可靠寿命迭代求解与优化计算迭代同步进行，显著提高计算效率；通过对某型车辆传动箱的结构可靠寿命优化设计结果表明该方法具有较好的效果和计算效率。

关键词：优化设计；可靠寿命；单循环；功能度量法

本文引用格式：刘勤，孙志礼，涂宏茂，等.基于单循环功能度量法的结构可靠寿命优化设计[J].兵器装备工程学报，2016(6):6-9.

Citationformat:LIUQin,SUNZhi-li,TUHong-mao,etal.StructuralReliableLifeOptimizationDesignBasedonSingle-LoopPerformanceMeasureApproach[J].JournalofOrdnanceEquipmentEngineering,2016(6):6-9.

结构载荷、材料性能及疲劳、磨损影响因素等的不确定性会导致机械结构寿命具有较大的变异性。可靠寿命考虑了影响因素的随机性，定义为结构给定的可靠度所对应的寿命单位数[1]。常规的结构优化方法由于难以系统考虑不确定性因素的影响，优化结果往往并不可靠[2-4]。以可靠寿命为目标的优化设计，在满足性能、结构布局、费用等条件下，力求使机械结构寿命最长、耐久度最高，从而有效提升产品的平均故障间隔时间等系统可靠性指标。

由于可靠寿命优化模型的目标、约束考虑了影响因素的随机性，其可靠寿命、可靠度计算为一个复杂的迭代计算过程，因此可靠寿命优化属于概率优化问题。在优化迭代计算过程中，需要采用转换的策略，按照一定的方式将可靠寿命目标、可靠度约束转换为确定性目标、约束，从而将概率优化转换为常规确定优化，再利用常规的优化算法实现求解。对于概率优化求解，主要有三类方法：双循环方法，单循环方法和解耦方法[5-8]。双循环方法采用两个嵌套的优化循环：设计优化循环(外层)和可靠度分析循环(内层)。单循环方法[9]是在双循环的基础上改进的，内层循环由单次可靠度计算近似代替，实现可靠性分析和优化计算的同步收敛，优化效率提升显著。

1　结构可靠寿命优化模型

工程中常以可靠寿命作为耐久性指标，如汽车底盘首次大修期B10≥10 000km，即要求90%的底盘寿命达到10 000km，才满足指标要求[10]。

若寿命函数表示为N(x，d)，式中d为设计变量向量，x为随机变量向量；给定可靠度R时，可靠寿命NR满足

(1)

式中，P{·}为概率函数。由此，可靠寿命函数表示为NR(x，d)。对于结构疲劳寿命的预计，工程常用的以下几类方法：应力寿命法、应变寿命法、断裂力学法、损伤力学法。应用上述方法，得到寿命函数N(x，d)，然后根据上述概率函数转换为可靠寿命函数。

根据可靠寿命为约束还是目标，结构可靠寿命优化模型一般可以分为2种：可靠寿命约束下结构费用、结构质量等极小化或性能最优化(简称可靠寿命为约束的优化模型)；在性能、费用、质量、强度、刚度、等约束下可靠寿命极大化或(简称可靠寿命为目标的优化模型)。这两种类型优化实质上是一致的，是同一个问题的两种不同表达方式。

1) 可靠寿命为目标的优化模型

在一些新的结构设计时，往往事先规定了费用、性能等的界限，可靠寿命要求越大越好。这类问题即为，在结构费用、结构质量等特性约束下可靠寿命极大化，其模型如下

(2)

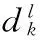
2) 可靠寿命为约束的优化模型

根据用户需求提出的耐久性指标，对结构进行设计，以可靠寿命为约束，性能、费用、质量等特性极小化，适合于此类设计，其模型如下：

(3)

式中，f(d)为目标函数，例如结构费用、质量、体积等的函数；Ng为耐久性指标，其他同前。

2　基于单循环功能度量法的结构可靠寿命优化求解

1) 结构可靠寿命优化求解流程

通过近似功能度量分析，每次进行确定性优化前将所有可靠寿命约束近似转换为线性约束。针对结构可靠寿命优化模型，利用单循环方法，如图3所示。

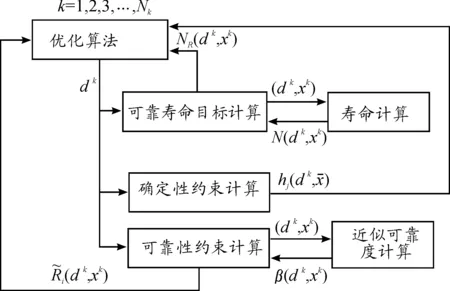
图1　基于单循环功能度量法的结构可靠寿命优化求解流程

在序列二次规划法(SQP)[11]等优化算法的每一次优化迭代步，增加在设计点dk处计算可靠寿命目标或约束、可靠性约束值，并将其转换成近似函数，实现优化求解与可靠寿命、可靠度求解的同步收敛，从而得到最优解和最优值(2)可靠寿命目标/约束的转换。

在优化迭代过程，利用功能度量法[12-13]，构造并求解近似规划问题前，将可靠寿命目标/约束在当前设计点处进行泰勒展开，转换成线性约束：

(4)

上式采用功能度量法的迭代公式进行一次近似可靠寿命分析，k表示优化迭代次数。若给定可靠度为R=φ(β)，β为可靠度指数，其中近似可能失效点根据以下2式计算

式中，▽uNu(dk-1,uk-1)是寿命函数关于随机向量u的梯度向量。

当设计变量是随机变量的统计参数时，设计变量梯度向量的对应元素由下式计算：

(7)

式中，▽uNu(dk-1,uk-1)可通过功能度量法的迭代公式求解，▽yu为标准正态变量对原设计变量概率分布参数的偏导数。

当设计变量是确定性参量时，设计变量梯度向量的对应元素由下式计算：

(8)

式中，hi为差分步长，ei为除第i个分量为1，其余分量为零的单位向量。

2) 可靠度约束的转换

利用可靠性优化方法对可靠性约束的转换，如对于第i个可靠度约束，令P{gi(d,x)≥0} =Φ(βi)，βi为可靠度系数；在优化迭代过程，该约束在当前设计迭代点转化为线性约束函数，即：

(9)

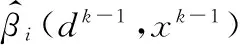
(10)

式中，Gi(dk-1，uk-1)是功能函数gi(dk-1，xk-1)由随机向量x转换至独立标准正态空间向量u后的函数；k表示优化迭代步序号；▽uGi(dk-1，uk-1)是Gi(dk-1，uk-1)对u的梯度向量。下一步迭代的uk由式(11)计算。

(11)

3) 优化求解

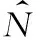
可靠寿命为目标的优化模型转换为：

(12)

可靠寿命为约束的优化模型转换为：

(13)

转换为常规的优化模型后，利用序列二次规划(SQP)等优化算法即可求解。

3　应用实例

某车辆传动系统的耐久性指标B10为10 000 km，对该箱体进行结构优化，问题可以描述为：在满足耐久性指标的情况下，通过优化箱体结构，减轻箱体质量，其一般模型表示为：

式中，Weight( )表示箱体的质量函数，LifeR=0.9()表示箱体可靠寿命函数。

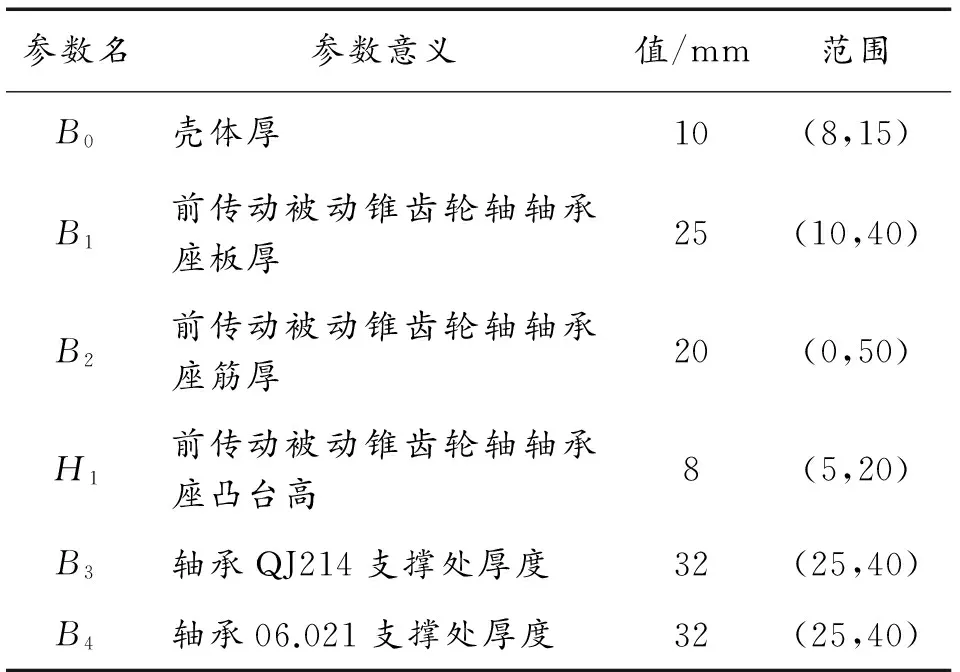
表1　箱体结构设计参数

经过有限元计算，获得箱体最大应力为132.3 MPa，在输入轴区域，如图2所示。为确定满足耐久性指标要求时允许的箱体初始裂纹尺寸最大值a0，故选取a0作为箱体设计参数，按保守设计，裂纹位置位于最大应力附近。

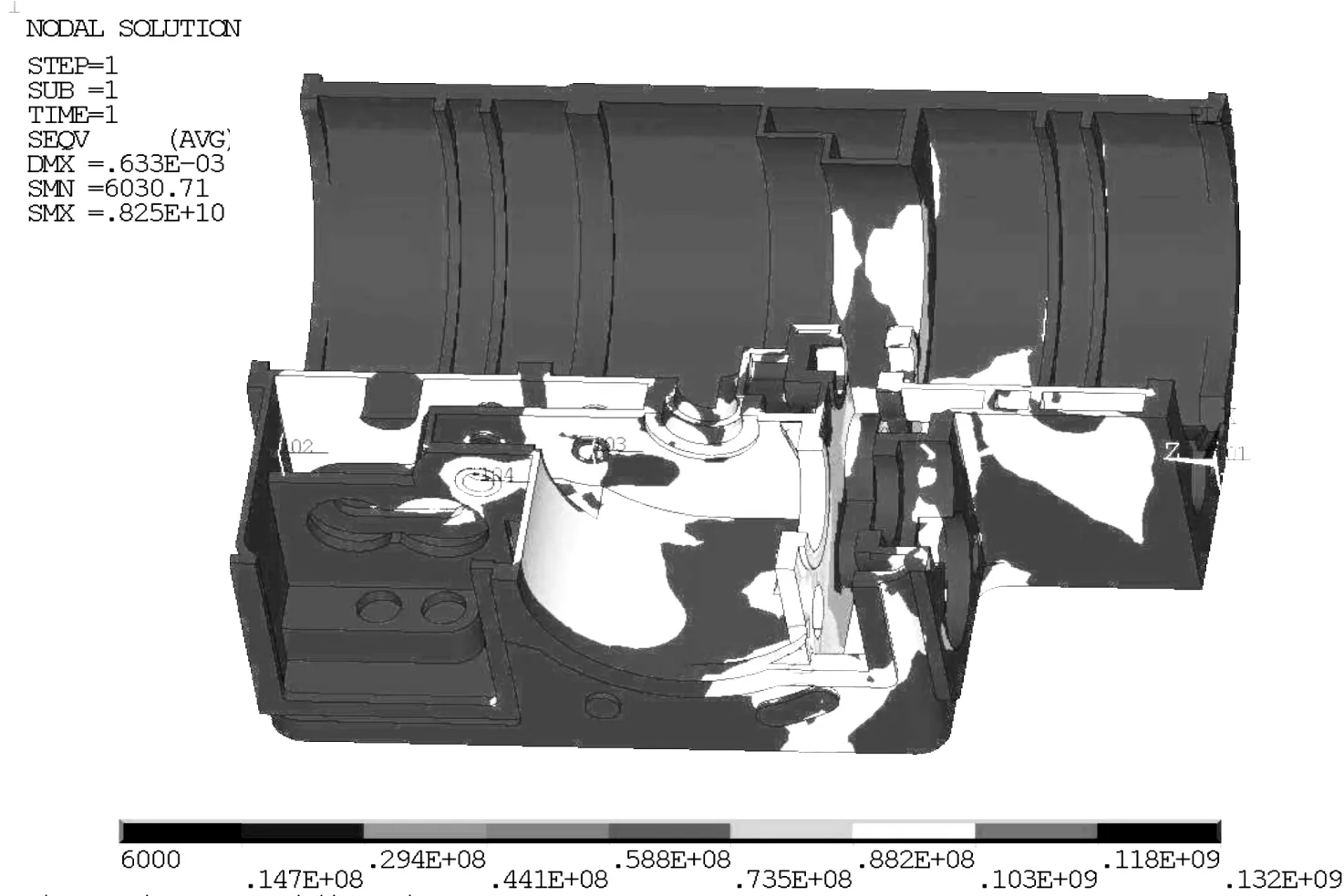
图2　箱体局部应力分布

利用Promrel软件，通过拉丁超立方设计生成100组试验样本，将箱体有限元分析参数化，编制APDL，并利用Paris公式计算裂纹扩展寿命。改变样本参数值，分别进行100次裂纹扩展寿命计算，拟合了箱体寿命的二次响应面模型，如下：

Life=262.4+1.3×10-2×B0-1.32×B1-

0.83×B2-0.73×H1-0.25×B3-0.15×B4-

1.3×10-5×E-2.2×10-4×B1×B2-

2.5×10-5×B1×B3+2.7×10-4×B0×H1-

8.3×10-4×B0×B3+0.011×B3×B4+

其中，E为材料弹性模量。箱体质量W的响应面函数为：

W=4.73×B0+0.115×B1+0.013×B2+

0.039×H1+0.175×B3+0.026×B4+219.4

为验证本文的方法，分别利用单循环功能度量法、双循环功能度量法进行了可靠寿命为目标、约束的优化求解，其结果列入表2。

表2　箱体结构耐久性优化结果对比

从表2中可以看出，可靠寿命为目标的结构优化获得了更长寿命的方案，可靠寿命为约束的结构优化获得满足耐久性约束下质量最轻的方案；对于可靠寿命优化，单循环功能度量法与双循环功能度量法优化结果相近，但单循环功能度量法的计算效率较双循环高14%；以常规寿命为约束的结构优化方案，虽然质量更轻，但经过验算后，发现该点的可靠寿命为8 600 km,不满足要求。

4　结论

本文将单循环功能度量法引入结构寿命优化设计，提出了一种以可靠寿命为目标、约束的结构优化设计方法；可靠寿命为目标的结构优化可获得更长寿命的方案，可靠寿命为约束的结构优化可获得满足耐久性约束下质量最轻的方案。该方法将可靠寿命的迭代求解，与优化计算的迭代同步进行，提高计算效率，这对于复杂结构优化设计具有重要的工程意义。

通过对某型车辆传动箱的结构可靠寿命优化设计，并与双循环功能度量法、常规寿命优化设计等计算结果相比较，表明基于单循环功能度量法的结构可靠寿命优化设计方法具有较好的效果和计算效率。相对于双循环功能度量法优化方法，单循环功能度量法的结果相近，但计算效率较双循环高14%；以常规寿命为约束的结构优化方案，虽然质量更轻，但经过验算后，发现该点的可靠寿命不满足要求。

参考文献：

[1]张银龙，申兆祥，卞士川，等．装备可靠性、耐久性与寿命之间的关系[J]．四川兵工学报，2013(8)：76-79.

[2]RACKWITZ R.Reliability analysis-a review and some perspectives[J].Structural Safety，2001，23(4):365-395.

[3]GUAN X F，HE J J，RASSELKORDE El M.Probabilistic Fatigue Life Prediction and Structural Reliability Evaluation of Turbine Rotors Integrating an Automated Ultrasonic Inspection System[J].J.Nondestruct Eval，2014，33:51-61.

[4]谢里阳，任俊刚，吴宁祥,等.复杂结构部件概率疲劳寿命预测方法与模型[J].航空学报，2015，36(8):2688-2695.

[5]RAMUP，QUX，YOUNB，etal.Inversereliabilitymeasuresandreliability-baseddesignoptimization[J].IntJReliabilityandSafety，2006，1(1/2):187-205.

[6]LIG，MENGZ，HUH.Anadaptivehybridapproachforreliability-baseddesignoptimization[J].StructMultidiscOptim(2015) 51:1051-1065.

[7]YOUNESA，ALAAC.Benchmarkstudyofnumericalmethodsforreliability-baseddesignoptimization[J].StructuralandMultidisciplinaryOptimization，2010，41(2):277-294.

[8]YIP，CHENGGD，JiangL.Asequentialapproximateprogrammingstrategyforperformance-measure-basedprobabilisticstructuraldesignoptimization[J].StructuralSafety，2008,30(2):91-109.

[9]LIMJ，LEEB.Asemi-single-loopmethodusingapproximationofmostprobablepointforreliability-baseddesignoptimization[J].StructMultidiscOptim，2015(11):1-13.

[10]刘勤，钱云鹏，姬广振，等．随机载荷作用下扭力轴耐久性优化设计[J]．兵工学报，2015(5)：933-937.

[11]袁亚湘，孙文瑜．最优化理论与方法[M]．北京：科学出版社，2005.

[12]RAHMANS，WEID.Designsensitivityandreliability-basedstructuraloptimizationbyunivariatedecomposition[J].StructMultidiscOptim，2008,35(3):245-261.

[13]LIL，LIUJH,LIUSH.AnefficientstrategyformultidisciplinaryreliabilitydesignandoptimizationbasedonCSSOandPMAinSORAframework[J].StructMultidiscOptim，2014(49):239-252.

[14]赵克刚，李健，姚伟浩．车辆传动系统固有特性的识别[J]．重庆理工大学学报(自然科学)，2014(4)：5-9．

(责任编辑周江川)

doi:【装备理论与装备技术】10.11809/scbgxb2016.06.002

收稿日期：2016-01-17；修回日期：2016-02-20

基金项目：总装备部预先研究项目(51319010402)；国防技术基础项目(Z092012B001)

作者简介：刘勤(1981—)，博士，副研究员，主要从事机械可靠性设计分析研究。

中图分类号：TH122

文献标识码：A

文章编号：2096-2304(2016)06-0006-05

StructuralReliableLifeOptimizationDesignBasedonSingle-LoopPerformanceMeasureApproach

LIUQin1,2,SUNZhi-li1,TUHong-mao1,2,JIGuang-zhen2

(1.SchoolofMechanicalEngineeringandAutomation,NortheasternUniversity,Shenyang110819,China; 2.OrdnanceScienceandResearchAcademyofChina,Beijing100089,China)

Abstract:The traditional structure life optimization doesn’t consider randomness of factors for fatigue, wear, etc. A structure optimization approach, which set reliabe life as object and took constraint structure optimization as the design method, was proposed by using single-loop method. The new sequential approximate programming realizes concurrent convergence of both design optimization and reliabe life calculation, and the present algorithm is more efficient. Finally, the optimization design of transmission case in vehicle was employed. The result demonstrates the good effectiveness of the presented method.

Key words:optimization design; reliable life; single-loop; performance measure approach