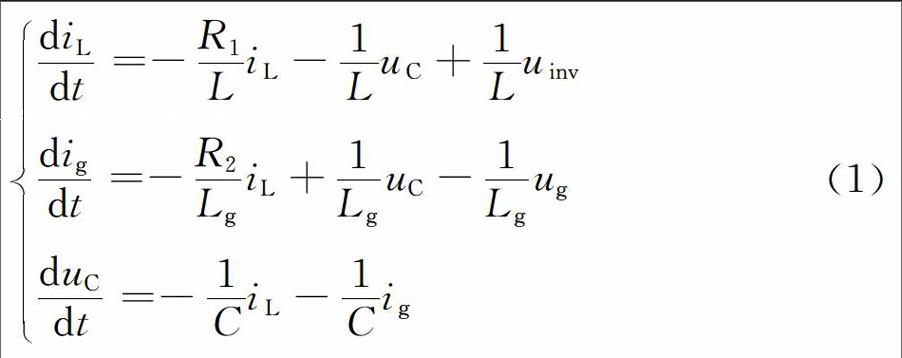LCL并网逆变器二自由度PID单电流有源阻尼方法
2016-08-12陈燕东王自力周乐明杨苓
陈燕东 王自力 周乐明 杨苓
摘要:提出了一种LCL并网逆变器二自由度比例积分微分(two degrees-of_fteedomPID control,2DOF-PID)单电流反馈有源阻尼控制策略,其由比例积分(PI)环节和不完全微分环节两部分构成。比例积分环节控制并网电流高质量接入电网;不完全微分环节增强LCL逆变器的阻尼系数,有效抑制系统与电网形成的谐振尖峰,提高系统可靠性与稳定性,并改善系统的动态响应速度。该方法不用增加电压和电流传感器,系统成本低。建立了2DOF-PID控制系统的传递函数,分析了系统的稳定裕度与动态特性,选取了合适的控制参数,构建了系统仿真模型和实验平台。仿真与实验结果表明:2DOF-PID控制的LCL并网逆变器的满载并网电流畸变率仅为2.2%,远低于国家标准(GB/T30427-2013)的要求;当系统从半载跳变到满载时,系统超调量低于9%,响应速度比其他方法更快。
关键词:并网逆变器;LCL滤波器;二自由度PID控制;谐振;有源阻尼
中图分类号:TM464 文献标识码:A
当前及未来几十年,人类面临化石能源逐渐枯竭及环境恶化的重大挑战,开发太阳能、风能、生物质能等新能源并实现并网发电是解决当前全球能源危机的必然趋势和选择。近年来以并网逆变器为接口的光伏并网发电系统取得了飞速发展,光伏屋顶、风光互补等分布式发电受到日益关注,并网逆变器是光伏发电系统的核心,为了减少无功损耗以及电流谐波的危害,要求逆变器输出功率因数高、输出电流谐波含量低。由于逆变器采用高频脉宽调制方式,会产生高次谐波危及系统安全与稳定运行,需要进行抑制或滤除。LCL滤波器因其高频谐波抑制能力强、总电感量及体积小,受到国内外广泛关注。同时,LCL滤波器中的网侧电感与变压器或电网阻抗相串联,还可有效降低电网阻抗变化对系统控制的影响。但由于LCL滤波器是一个低阻尼三阶系统,易产生谐振造成系统不稳定,因此对系统提出了必要的阻尼控制功能。
现有LCL并网逆变器的谐振抑制包括无源阻尼和有源阻尼两种方式。无源阻尼法通过在LCL滤波电容支路中串联或并联阻尼电阻,从而增加系统阻尼,抑制LCL滤波器的谐振尖峰,其易于实现。但无源阻尼串并联电阻上存在有功损耗,同时还将会削弱LCL滤波器对高频谐波的抑制效果。因此,无源阻尼方法通常被有源阻尼方法所取代。有源阻尼通过增加额外的反馈控制,如分裂电容法、零极点配置补偿法,以及电容电流补偿法等获得与无源阻尼同样的谐振抑制效果,实现方式灵活方便,且不会增加额外功耗。文献提出采样滤波器电容电流并进行反馈控制,其能够增加系统阻尼程度,实现简单灵活,但由于滤波器高频电容电流幅值较小,增加了采样精确处理控制变量数据的难度。文献提出采用滤波器网侧电感电压微分量反馈实现谐振尖峰的抑制,文献提出通过反馈滤波器的电容电压微分量实现增加系统阻尼,然而微分环节在实际工程中引入了噪音干扰信号,增加了设计难度。上述方法除了对并网电流闭环控制所需的并网电流传感器之外,均还需额外的电压/电流传感器,这不仅增加了系统硬件成本,还降低了系统可靠性。文献提出一种采用并网电流两次微分的反馈方法,实现谐振阻尼控制,无需增加额外传感器,但并网电流导函数将会带人噪声放大,造成系统振荡。
对此,本文提出了一种LCL并网逆变器的2DOF-PID单电流有源阻尼方法,该方法包括比例积分环节和不完全微分环节两部分,其中,比例积分环节实现并网电流高电能质量接人电网;不完全微分环节不仅增大了LCL滤波器的阻尼系数,有效抑制逆变器输出电流的谐振尖峰,而且还大幅提高了并网逆变器的动态响应速度、降低了系统超调量。在此基础上,文中合理设计了2DOF-PID控制器参数,并通过仿真与实验验证了该方法的有效性。
1 LCL光伏并网逆变器数学模型
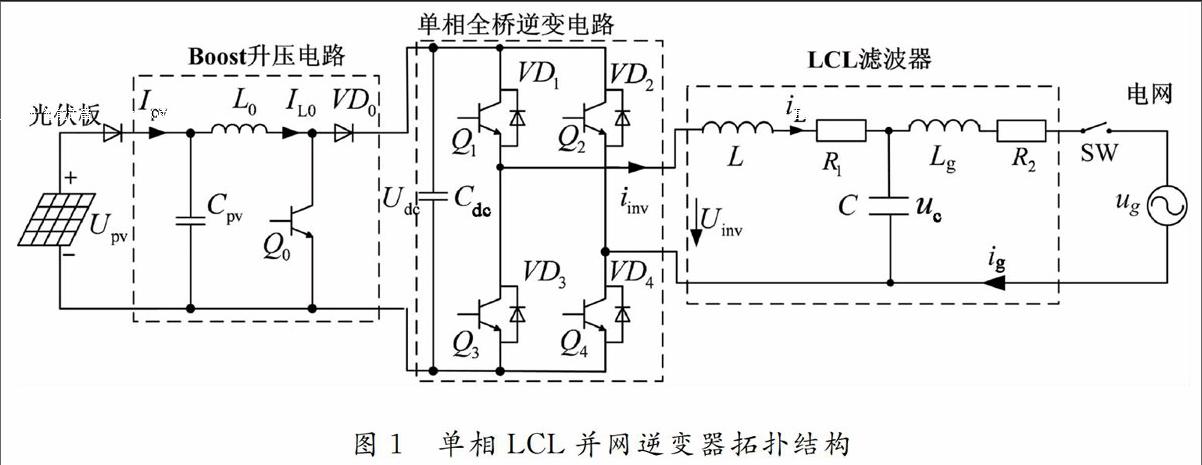
图1为单相LCL光伏并网逆变器电路结构图。主要包括光伏阵列、Boost升压电路、全桥逆变电路、LCL滤波器。其中,Boost升压电路将光伏阵列侧能量传送到全桥逆变器的输入直流侧,同时,完成最大功率跟踪控制功能,逆变器经LCL滤波器进行滤波后,将直流侧能量以高功率因数、低谐波含量的交流电馈送至电网。图1中,upv和ipv分别为光伏阵列的输出电压和输出电流;ug和ig分别为电网电压和并网电流;iinv,iL分别为逆变器输出电压和电流;uc为滤波电容电压;电感L,电容C以及电感Lg构成LCL滤波器;R1,R2分别为电感L,Lg的寄生电阻,SW为并网开关。
根据基尔霍夫KVL,KCL定律,选取逆变器侧电感电流iL,并网输出电流ig及滤波电容电压uC为变量,可得LCL逆变器的状态空间方程为:
由式(1)可以得到LCL型逆变器系统的模型框图,如图2所示。若将电网电压ug作为扰动信号,可推导出逆变器输出电压uinv到并网电流ig的传递函数为:
2 传统单电流反馈有源阻尼方法
有源阻尼方法能够很好抑制LCL滤波器的谐振尖峰,目前大量的研究主要集中在电容电流/电压的反馈控制上,其增加了系统阻尼,提高了谐振尖峰抑制能力,但需要增加额外的传感器,增大了系统的设计难度。文献采用逆变器并网电流的两次微分反馈方法能够克服上述问题,如图3所示。逆变器指令信号um到并网电流ig的传递函数:其中,Kinv为调制波到逆变器输出电压的传递函数,Ksd为两次微分的反馈系数。
式(3)的标准形式为:
由此可知,通过调节反馈系数Ksd,可以得到相应的阻尼系数,并网电流的两次微分(s2)环节能够实现LCL型并网逆变器谐振尖峰的抑制,且无需额外的传感器,提高了系统可靠性,但并网电流导函数将带来噪声放大,造成系统振荡,并影响系统稳定,且反馈参数也不易选取。针对上述不足,本文在并网电流两次微分策略的基础上,进一步提出单电流反馈中可等效成系统阻尼部分的方法,实现增加系统阻尼,减少引入放大的噪音信号。
3 二自由度PID并网控制策略
二自由度PID控制方式是在传统一自由度PID控制中设法整定两套可以独立整定的PID参数,从而使受控系统的目标跟踪特性和干扰抑制特性能同时达到最佳状态的控制方式。
基于上述特性,本文采用二自由度PID控制策略,该方案由比例积分PI控制器及不完全微分的微分先行算法构成,如图4所示。
其中,微分先行表示为只对并网电流ig进行微分,而不对并网指令信号ig*进行微分,不完全微分表示为微分环节加入一阶惯性环节,可有效抑制高频干扰,改善系统动态性能。
二自由度PID控制器中PI控制器(控制参数分别为Kp和Ki)作为前向通路控制器,D为反馈环节的微分部分。其中D等于并网电流通过低通滤波器后的微分,可表示为:
其中,Kd为微分环节的反馈系数,td为低通滤波器的时间常数。
仅考虑微分环节D,则在谐振频率ωres处,LCL型逆变器的调制信号um(jωres)到并网电流ig(jωres)的传递函数可表示为:
当Gd0(jωres)D(jωres)实部呈负时,为负反馈控制,系统能够稳定运行,当|D(jωres)|不断增大,传递函数Gd(s)的增益在ωres逐渐变小,谐振抑制效果将会越来越好,因此只要合适设计微分环节D能够实现谐振尖峰的抑制。
引人二自由度PID控制策略,忽略滤波器的寄生电阻,逆变器调制信号um到并网电流ig的传递函数Gd(s)为:
根据式(9)可知微分环节D引入了一个额外的极点与零点,但合理设计微分环节参数可使额外的极点位于s域的左半平面,不影响系统稳定性,图5给出了开环传递函数Gd(s)的波特图。其中ξ1为2DOF-PID策略下系统的目标阻尼系数,ωn为引入反馈后的谐振频率,K为引入的极点到虚轴的距离与共轭复数极点到虚轴距离的比例系数。
根据同次幂的系数相同有:
据式(9)及图5可知,阻尼系数a增加了系统阻尼,实现了LCL型逆变器的谐振尖峰的抑制。且根据式(10)可得,调节参数Kd,td可获得所需的阻尼程度。
根据式(8)可得到LCL型逆变器的开环传递函数Gs-open及闭环传递函数Gs-close为:
根据式(11)给出了闭环传递函Gs-close的单位阶跃,如图6所示。由于不完全微分环节D可改善系统的动态性能,不同Kd与td的取值,2DOF-PID控制器对系统的调节时间不同。
综上所述,在LCL型逆变器并网控制系统中,2DOF-PID控制器中的目标滤波器能够增加系统阻尼,抑制并网逆变器系统的谐振尖峰;而且不完全微分环节可改善逆变器的动态响应速度,提高系统动态性能。工程上仅需对并网电流进行采样,无需额外的传感器,降低了硬件成本,提高了系统可靠性和静动态性能。
4 2DOF-PID控制器设计
2DOF-PID控制器存在4个控制参数:Kp,Ki,Kd,td。为了合理设计参数值,本文设计方案为:微分环节Kd,td考虑系统的响应速度及阻尼系数;PI控制器仅需保证系统的幅值裕度GM和相位裕度PM。基于上述设计方案,给出系统各控制参数。
由式(8)可得,增益为Kd和td的广义开环传递函数分别如式(12)和式(13)所示:
图7给出了增益为Kd的广义开环根轨迹,取td=3.56×10-5rad/s;图8给出了增益为ωg的广义开环根轨迹,取Kd=15。系统存在3个极点,其中λ1,λ2是一对共轭极点,λ3是实数极点,图中箭头对应相应参数增大的方向。
据图7可得Gd1(s)的大部分极点位于左半面,系统处于稳定状态。随着Kd的取值增大,共轭极点逐渐远离虚轴,系统响应速度减慢,系统阻尼系数逐渐增大,对谐振尖峰的抑制效果变强;当Kd取值过大时,实数极点进入右半面,系统将会处于不稳定。
如图8所示,随着td的减少,实数极点逐渐远离虚轴,共轭极点靠近虚轴成为主导极点,系统动态响应速度由开始的减慢到逐渐加快,则td取较大值时,系统将具有较短的调节时间。
根据图7和图8的根轨迹可知,增大Kd或td可增加系统阻尼,提高对LCL滤波器谐振尖峰的抑制;减少Kd或增大td可提高系统动态响应速度。
根据劳斯稳定判据,当系统处于稳定状态时,Kd和td的关系应满足:
0
根据图7和图8以及式(14),考虑LCL并联逆变器系统的谐振抑制效果及动态响应速度,本文合理选取Kd=19,td=4×10-5。
根据确定的微分环节控制参数取值,进而选择PI控制环的参数,考虑系统控制延时及采样延时,依据文献可得到控制参数为:
其中,fc为传递函数Gs-open的穿越频率。选取Kp=0.45,Ki=100其中幅值裕度GM为4.8dB,相位裕度PM为48.9°,稳定裕度满足工程应用的需要。
5 仿真与实验平台搭建与验证
本文利用Matlab/Simulink软件搭建了LCL并网逆变器系统的仿真模型,控制参数如表1所示。系统开关频率fc为12.8kHz。
加入微量扰动信号19800rad/s,验证系统的谐振抑制效果以及稳定性能。引入2DOF-PID控制,与无谐振阻尼控制相比,并网电流ig波形趋于光滑,谐振尖峰得到明显抑制,如图9所示。
搭建了一台2kW单相并网逆变器样机,如图10所示,功率器件选用三菱公司的IPM模块PM505LA060,DSP采用TMS320F2812,样机参数如表1所示。
图11为2DOF-PID控制策略下的并网电流波形和谐波分析。测得并网功率因数PF=0.998,并网基波有效值8.18A并网畸变率仅为2.2%,远低于国家标准5%,实现了光伏能量的高电能质量接人电网。
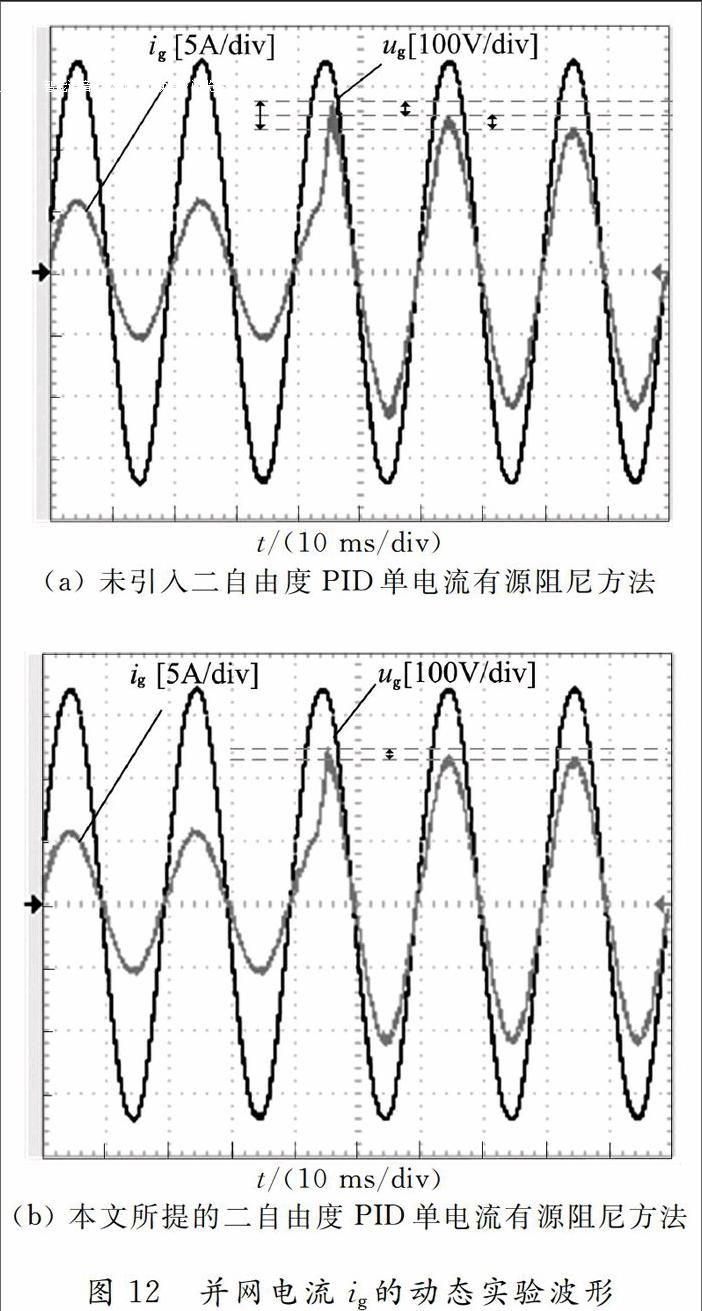
图12为并网电流给定值由半载跳变到满载的实验波形。与未采用2DOF-PID控制相比,提出的2DOF-PID单电流有源阻尼方法使得系统在暂态过程的超调量从26%下降到9%。本方法使得逆变器并网电流波形在突变后的下一个工频周期便能稳定运行,且响应速度快、超调量少,具备很好的稳态与动态性能。
6 结论
现有LCL并网逆变器有源阻尼控制方法需增加多个电压和电流传感器,且易振荡,致使系统稳定性变差。本文提出了一种2DOF-PID控制的LCL并网逆变器单电流有源阻尼方法。该方法包括比例积分环节和不完全微分环节两个部分。不完全微分环节的引入增强了LCL并网逆变器的阻尼系数,有效抑制了系统谐振,并改善了暂态过程的响应速度与超调,且该方法不需要增加电压和电流传感器。系统仿真实验与样机运行结果验证了所提方法的正确与有效性。该方法可推广到光伏屋顶分布式发电、微电网逆变器中,为解决新能源高电能质量接人电网提供了新途径。