基于环形磁场励磁的两面磁力抛光试验研究

阮日新　罗虎　王永强　陈逢军　胡天　尹韶辉

摘要：磁力抛光多数以单面抛光为主，较少有双面同时有效抛光方式。本文提出了基于环形磁场励磁的磁力抛光新工艺，该方法可以同时有效抛光两个表面。通过设计能励磁环形磁场的电磁铁，并进行三维有限元仿真分析，搭建了环形磁场双面抛光装置。利用该平台进行不锈钢两面抛光工艺试验研究，探讨了电流强度、磁极与工件间间隙、主轴转速和抛光时间工艺等参数对表面粗糙度R_a的影响。得出表面粗糙度R_a随着抛光时间、工作间隙、工件转速的增大而减小。设计正交实验方案得出合理的两面磁力抛光工艺参数，并最终取得了具有良好表面粗糙度R_a的两面工件样品。试验证明，该方法可以同时对工件的两个表面进行抛光，两个表面的表面粗糙度R_a由最初0.2μm下降到R_a（S）=0.094μm和R_a（N）=0.068μm。

关键词：磁力研磨；环形磁场；两面抛光；磁场仿真

中图分类号：TH161 文献标识码：A

磁力抛光加工具有比较好的柔性、自适应性、自锐性、可控性，无须进行工具磨损补偿与修形。磁力抛光克服了传统精密研磨抛光方法在加工非规则形状的容器内壁、弯管内表面、微细管内面，去除内孔毛刺、交叉孔毛刺，抛光模具复杂曲面等方面的不足。磁力抛光对于解决复杂型面光整加工有特定的优势，近年来引起了广泛重视。

国内外已研究出多种磁力研磨抛光工艺。前苏联于20世纪70年代，研制出了8MN系列平面磁力研磨机床，开发了平面磁力抛光工艺。日本学者Shinmura将磁力抛光工艺拓展至加工外圆、内圆、曲面、球面等难加工工件，并对相应的磁力加工原理、不同参数下光整加工特性和影响因素进行了研究。尹韶辉等借助振动与磁力抛光复合方法对复杂凹凸类零件进行抛光，认为磨料颗粒大小影响工件内部表面质量素。Jeong-DuKim等为实现自动控制磁力抛光，研制了基于计算机控制的旋转磁场磁力研磨加工系统。胡德金等设计了新型回转磁场装置，能同时产生往复磁场和回转磁场，并对多种材料管状工件内表面进行了磁力抛光试验。许雪峰等提出了一种磁性复合磨粒化学机械抛光新工艺。

另一方面，磁力抛光较低的加工效率是制约其走向工业应用的重要原因。为提高磁力抛光技术的效率，国内外学者做了一些研究。如Shinmura在对磁力抛光原理和工艺进行深入的理论分析后，研究了加工间隙、磁场强度、磁性磨粒的成分和粒度、磨料与工件的相对移动速度等因素对加工效率和质量的影响。尹韶辉等在利用振动辅助对镁合金进行磁力抛光试验时，加工工件的表面质量和去除量得到提高。李亿勋等人借助二维振动对304不锈钢进行磁力研磨实验，实验结果表明，二维振动磁力研磨不仅能提高工件的表面质量，而且能提高去除效率。

目前磁力抛光主要以单面抛光为主，对同时双面抛光研究较少。双面抛光能明显缩短抛光时间，有利于生产效率的提高。本文提出一种基于环形磁场辅助的磁力抛光新工艺，可以同时对相应零件进行双面抛光，通过采用田口法设计正交试验方案，对电流强度、工作间隙、主轴转速和加工时间等参数进行工艺实验研究。

1 双面磁力抛光原理及装置

环形磁场两面磁力抛光原理如图1所示，主要包括电磁铁、夹具、工件轴。环形间隙中填满抛光粉。工件装夹在一个特定尺寸圆盘形夹具上，该夹具与立式铣床的主轴相连，夹具和工件可以随着立式铣床的主轴旋转，并且旋转速度可以调节。工件与电磁铁铁芯间的距离为工作间隙δ_w。磁力抛光加工时，电磁铁接通直流电源后，铁粉颗粒在环形磁场中组成一条条沿径向分布的磁链，从而形成强粘度的磁力刷。当工件在环形间隙中作切割磁链运动时，使原来一条沿径向分布的磁链断裂成两条，从而形成了两个微小刷头；这两条暂时断裂的磁链在磁场的作用下有相互愈合的趋势，会挤压均匀分布于这些磁力刷头之中的磨粒，使磨粒与工件的两个表面相互作用实现材料的去除，以达到同时光整加工工件两个表面的目的。

励磁系统是磁力抛光实验装置的关键，其主要包含具有环形间隙结构的电磁铁，电磁铁主要由直流电源、线圈、铁芯、导磁板等组成。当提供一个直流电流给线圈后，线圈环绕的铁芯会被磁化，形成一个圆柱形磁铁。当铁芯与纯铁材料制成的导磁板相连时，电磁铁会经由导磁板间形成一个闭合回路。如果将上导磁板开一个圆孔，使圆孔与圆柱铁芯同心且保留一定的间隙，当该间隙很小时，不会影响磁路的形成，这样在上导磁板与铁芯间会形成一个径向的环形磁场。改变通往线圈电流的大小可以得到不同磁场强度的环形磁场，电流可调节的范围是0.25A至6A。

磁力抛光试验装置由立式铣床和自行研制的励磁装置组成，如图2所示。

2 磁场有限元分析

2.1 Maxwell有限元仿真模型及结果

使用Maxwell软件建立励磁电磁铁三维有限元分析模型如图3所示。该模型中铁芯和导磁板的材料都选工业纯铁。线圈匝数为300，厚度为90mm，线圈的轴向长度为100mm；工业纯铁的相对磁导率根据纯铁的含铁量分为6000到240000不等，本文选用默认值10000；空气的相对磁导率为1。采用软件默认方式自动生成网格，激励源为电流，大小为3A。对于3D静磁场分析，以空气环境包围整个区域的求解域，与所需要的磁场边界条件满足无限远边界条件。

经过仿真计算，得到电磁铁的磁场强度分布如图4所示，环形间隙的磁感应强度介于1.25T至1.43T。图4（a）显示电磁铁在其环形间隙处形成的磁场强度均在1T以上，且沿径向方向分布均匀。磁场分布越均匀，磁力抛光时形成的剪切力变化越小，对工件原有的表面形状精度影响就越小。能使工件在保持原有形状精度的条件下，快速提高其表面粗糙度R_a，获得高精度、高质量的表面。图4（b）是磁场在环形间隙中沿纵向方向的磁感应强度分布，磁感应强度可以明显分为三个梯度，环形间隙上部纵向均匀性较好，环形间隙底部均匀性稍差。双面磁力抛光时，工件主要位于环形磁场的上部磁场中加工，有利于提高抛光表面各点的材料去除率和表面质量的均匀性。

2.2 Maxwell有限元仿真数学基础

麦克斯韦方程组是适用于所有宏观电磁现象的数学模型，是电磁场理论的基础，也是工程电磁场数学分析的出发点。麦克斯韦方程组微分形式：式中：H为磁场强度，A/m；，为电流密度，A/m²；D为电通量密度，C/w²；E为电场强度，V/m；B为磁感应强度，T；p为电荷密度，C/m³。

联立方程（1c）和（1d）即可得电磁场静磁场分析的方程组：

以上方程组是电磁场有限元方法分析的理论基础。有限元法以变分原理为基础，把要求解的微分方程型数学模型应用于有限元计算中，通常先将方程化为二阶方程，再将二阶方程进行有限元数值求解。三维静磁场的二阶齐次方程组为：式中ε为介质的介电常数，F/m；δ为介质的电导率，s/m；μ为介质的磁导率，H/m；Φ为标量电势。对于各项同性介质，ε，δ和μ是标量；对于各项异性介质，ε，δ和μ是张量。

2.3 磁感应强度测量

为验证仿真数据的可靠性，测量在离电磁铁上端面向下5mm处，由N极向S极沿径向方向测量环形间隙中的磁感应强度的分布情况，如图5所示。可以看出沿径向方向磁感应强度先减小后增大，且关于间隙中心对称，但靠近N极的磁场强度略大于S极。磁场在空气中衰减很快，距离导磁板和铁芯越远，磁感应强度越弱，故环形间隙中心磁感应强度最小。圆柱电磁铁形成的磁感应线从圆柱铁芯出发，经导磁板和环形间隙，最后回到铁芯形成一个闭合回路，在这个过程中空气的相对磁导率远远小于铁芯和导磁板，故产生的磁场在环形间隙中衰减最快，使N极附近磁场强度略大于S极，形成一个类似“V”型的磁场。

磁感应强度介于1.08T～1.26T，与仿真计算值1.25T～1.43T误差为11.8%～13.6%。由于实际所用的材料属性，机械加工过程中的开孔、螺纹等，与有限元模型有偏差；数学模型也不可能完全如实反映实际模型的数学关系，故该误差是可以接受的。

3 抛光试验条件

3.1 试验材料

选择不导磁材料SUS202不锈钢薄片（25×60×3）为试验材料。实验工件预先用传统方法进行抛光，使其表面粗糙度R_a值约为0.2μm。

3.2 试验方案

为研究抛光时间对工件表面粗糙度R_a的影响，选取一不锈钢薄片进行磁力抛光试验。试验前，测量其表面粗糙度R_a，随后每加工30min后，测量其表面粗糙度R_a，直至加工时间到180min。整个过程保持试验条件I=2A，δ_w=3mm，n=100r/min与装夹条件不变。

选取工作间隙δ_w，转速n，加工时间t作为试验参数，实验方案按照田口法设定，按照3个变量和3个水平变化，如表1所示。选用正交表L₉（3³）进行正交实验。试验中，将工件靠近电磁铁是南极S面的表面粗糙度记为R_a（S），靠近电磁铁北极N面的记为R_a（N）。

4 试验结果与分析

4.1 抛光时间对表面粗糙度R_a的影响试验

试验前用砂纸对选取的不锈钢薄片进行抛光，以保证其两面表面粗糙度值相近，约0.3μm。试验结果如图6所示。

由图知，表面粗糙度R_a随着抛光时间的延长，先急剧减小，后减小缓慢，最后趋向于饱和。抛光初期，工件原始表面质量差，工件表面绝大部分尖锐凸起部分与磨粒相互作用被去除，表面粗糙度R_a值下降较快；随着抛光的进行，工件表面越来越光滑，磨粒与工件的相互作用越来越弱，表面粗糙度R_a值下降放缓；随后，受到磨粒本身粒度的限制，抛光时间增长，表面粗糙度R_a值达到饱和状态。

60min前，R_a（S）值下降得比R_a（N）快；60min以后，R_a（S）值下降得比R_a（N）慢，并且先达到饱和状态，且最终R_a（S）饱和值比R_a（N）饱和值大。这是因为当δ_w为3mm时，近S极面磁感应强度比近N面要大，从而磁力抛光时磨粒受到磁链的压力越大，使得磨粒与工件表面相互作用的剪切力越大，使前期去除工件表面材料更多，故抛光初期近S极表面粗糙度值下降得快，抛光后期R_a（S）值先达到饱和值。表面粗糙度值与磨粒切入深度有关，切入深度越大，表面粗糙度值越大。磨粒的切人深度与磨粒所受到的压力有关，压力越大，磨粒切入工件表面越深，而双面磁力抛光中，压力受环形磁场中磁感应强度的控制，磁感应强度越强，形成的磁链对磨粒的压力就越大，故R_a（S）饱和值比R_a（N）饱和值大。

4.2 不锈钢磁力抛光优化试验

采用正交法进行试验，分析工艺参数δ_w，n，t对抛光后不锈钢表面粗糙度R_a的影响，并得出三因素三水平下最优工艺参数组合。选用L₉（3³）作为试验分析的正交表，试验结果如表2所示。

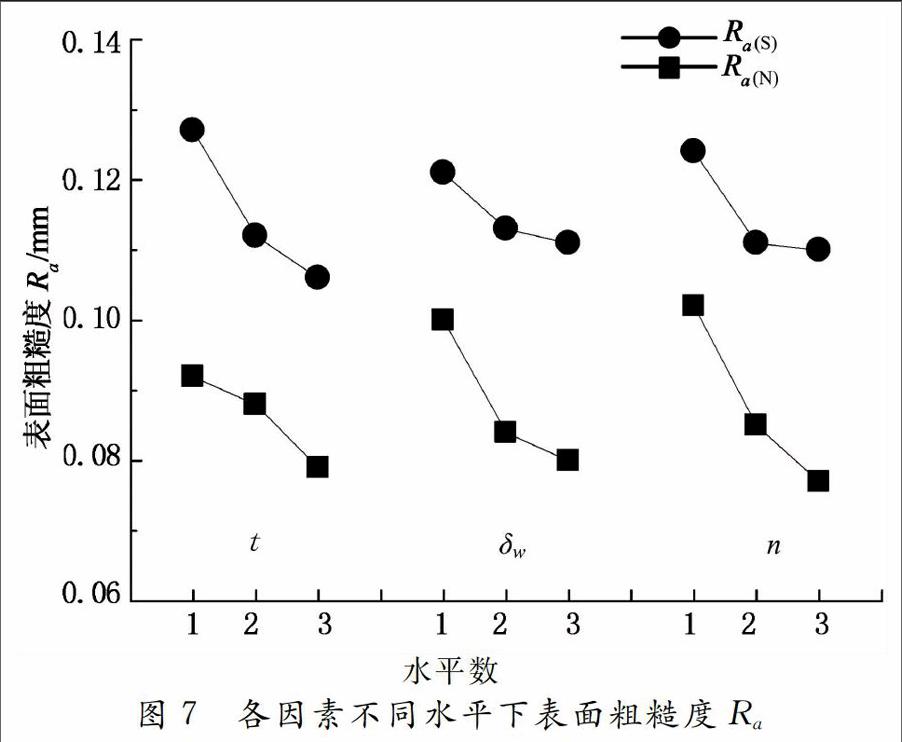
由表2知，三个因素每个水平均出现三次，为减少试验过程中误差对试验结果的影响，取三次的平均值进行分析，结果如图2所示。

由图7知，R_a（S）普遍比R_a（N）大，这是因为近S极加工工件表面的磁感应强度大于近N极的缘故，磁感应强度越大，磁性颗粒挤压抛光颗粒作用于工件表面的压力越大，故磨粒切入越深，磨粒刮擦、划刻工件表面留下的痕迹越深，因而表面粗糙度值越大。

表面粗糙度R_a随着抛光时间、工作间隙、工件转速的增大而减小。抛光时间越长，磁力抛光作用越充分，故表面粗糙度R_a小；工作间隙越大，环形间隙中的磁感应强度越小，形成的磁链对磨粒的压力越小，磨粒切入工件表面的深度越浅，因而磁力抛光后残留的痕迹越浅，故表面粗糙度R_a小；工件转速越高，单位时间内与工件表面相互作用的磨粒数量越多，提高了抛光效率，磁力抛光更充分。

工作间隙δ_w，抛光时间￡和转速n对R_a（S）和R_a（N）的影响趋势相同，故δ_w=3.5mm，t=60min，n=120r·min^-1时为最优。

电流强度I对R_a（S）和R_a（N）的影响不同，为获得其最优参数，需要综合极差分析。

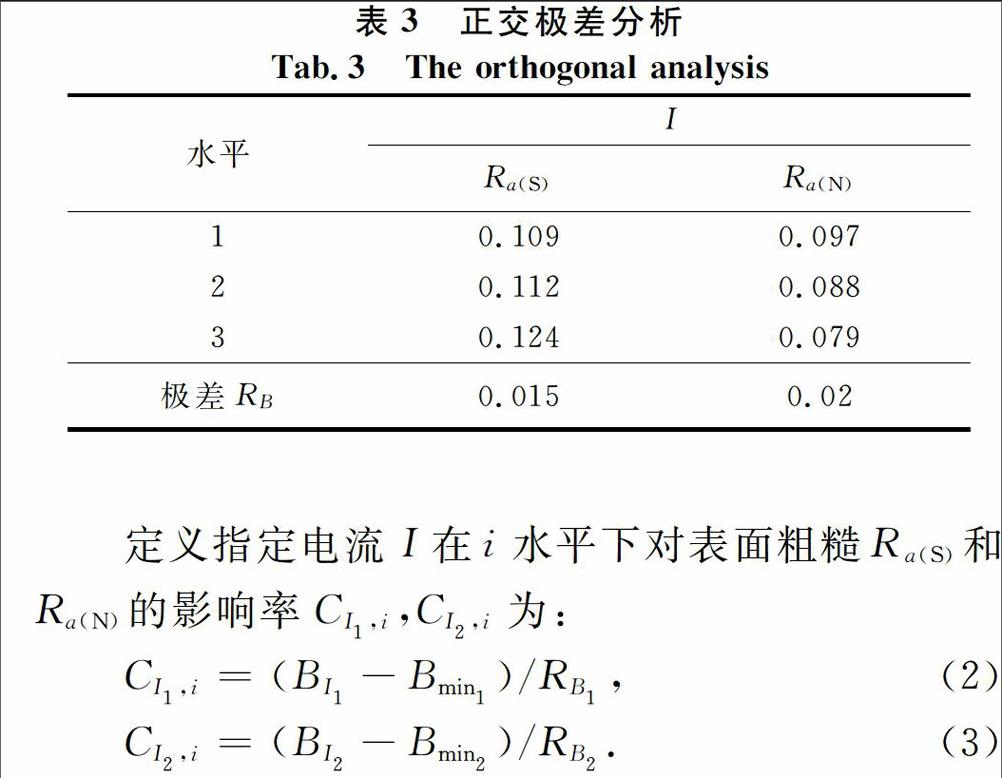
定义指定电流I在i水平下对表面粗糙R_a（S）和R_a（N）的影响率C_I1，i，C_I2，i为：

其中B_I为指定电流在i水平下的表面粗糙度R_a，B_min和R_B分别为该电流和时间三个水平下的最小表面粗糙度R_a和表面粗糙度R_a极差。C_I，i越小，表示指定电流在i水平下对表面粗糙度R_a的影响程度越小，可获得的表面粗糙度R_a越小。根据式（2），式（3）和表3计算电流在各水平下对表面粗糙度R_a的影响率，如表4所示。

定义指定电流在i水平下对表面粗糙度R_a（S）和R_a（N）的综合影响率C_I，i为：

C_I，i越小，表示该电流强度水平下对表面粗糙度R_a（S）和R_a（N）的综合影响率影响越小，此时，可获得较小的R_a（S）和R_a（N）。根据式（4）对表4求和，计算电流，各水平下对表面粗糙度R_a（S）和R_a（N）的综合影响率，如表5所示。

取综合影响率最小值确定电流I为I₂。因此尺寸的理想组合为I₂t₃δ₁n₃，即：I=2.5A，t=60mim，δ_w=3.5mm，n=120r·min^-1。

4.3 试验验证

为验证优化后工艺参数的可靠性，保持其它条件不变，在最优参数即：I=2.5A，t=60mim，δ_w=3.5mm，n=120r·min^-1条件下进行试验。获得了最好的试验结果：R_a（S）=0.094μm和R_a（N）=0.068μm，小于磁力抛光工艺试验表面粗糙度R_a。不锈钢薄片两面抛光后与原不锈钢薄片实物对比图如图8所示。

抛光时间40min后，在VHX-1000超景深三维数码显微镜2500倍下测量的结果如图9所示。抛光前，经过粗加工的不锈钢表面质量非常差，表面损伤严重，加工后残留痕迹多。抛光40min后，绝大部分表面损伤已经被去除，仅留下少量较深的痕迹。由于近S面磁感应强度比近N面要大，故R_a（S）=0.094μm大于R_a（N）=0.068gm。

5 结论

1）提出了一种基于环形磁场的磁力抛光方法，可以同时对工件的两个表面进行抛光，以不锈钢薄片作为试验材料进行试验，两个表面的表面粗糙度R_a得到大幅降低。

2）设计正交试验方案，进行工艺试验，得到环形磁场下磁力抛光最优工艺参数并进行试验验证，最终得到R_a（S）=0.094μm和R_a（N）=0.068μm的试验结果。