CVT锥轮推力平衡模型及影响因素研究

张飞铁　王建德　周云山　张明华

摘要：为提高无级变速器速比控制的精度与稳定性，研究了主从锥轮推力的关系及其影响因素。采用理论分析与试验验证相结合的方法，建立了主从锥轮推力比的数学模型，通过台架试验验证了模型的正确性，并且，通过台架试验研究了速比、转矩比、输入转矩与主动轮转速平衡推力比的影响。结果表明，平衡推力比与主从锥轮工作包角的比值成比例关系；推力比与速比呈单调递减的关系；同一速比下，输入转矩越大，推力比越大；推力比随转矩比的增大而线性增大，针对同一转矩比，最大转矩值越大，推力比就越小；主动轮转速对推力比的影响可以忽略。本文研究了推力比的平衡机理，为速比的精确控制提供了理论与试验依据。

关键词：无级变速器；锥轮推力；模型开发；因素分析

中图分类号：U463.212 文献标识码：A

随着国内自主开发的自动变速器的发展，无级变速器（CVT，continuouslyvariabletransmission）正成为国内的研究热点。无级变速器中的核心部件——变速机构影响着变速的平顺以及稳态速比控制的精度，变速的平顺性会影响整车的驾驶感觉，而速比的精度会影响整车的油耗。在油耗试验中，稳态工况速比的控制精度对油耗的影响明显。为了消除速比误差，目前常用的方法是运用速比反馈控制。但是，当实际速比误差过大时，反馈控制难以修正误差，这会导致整车油耗增大，严重时还会引起速比波动，这一现象在批量生产中较易显现出来。经过前期的初步研究，发现基于无级变速器的推力平衡，对速比实行前馈控制或基于模型的控制，能有效地消除速比误差与速比波动。因此，为提高速比控制精度与稳定性，有必要研究金属带式无级变速器变速机构的推力平衡模型及其影响因素。

由于变速机构的重要性，多个研究单位从不同方面对变速机构进行了研究。Kim从理论与试验的角度分析了金属片的受力特征，并使用速比转矩轴向推力的关系分析了金属带与锥轮的滑移特性。Tohru Ide使用超声波技术测量了无负载时不同夹紧力工况下的锥轮与金属带之间的作用力。Takeshi为说明CVT的传动机理建立了数学模型，并分析了作用在金属带上的稳态作用力与瞬态作用力。Akehurst从金属带效率损失的角度建立了数学模型，分析了金属带的受力情况，认为转矩损失是由于带与金属片以及带与锥轮的相对运动引起的。Hiroki从理论角度分析了CVT的传动机理并做了试验验证。Hirajo为橡胶带开发了仿真模型并计算了轴向推力。薛殿伦使用遗传算法对金属带受力进行了优化。但上述论文均没有对与速比控制相关的推力平衡进行研究。

本文分析金属带的受力情况，建立锥盘推力理论平衡模型，并通过试验分析了速比、转矩、转矩比以及主动锥轮转速对锥盘推力平衡的影响。

1 推力平衡模型

本文研究的CVT是国内某公司针对A级车自主开发的一款无级自动变速器，它由以下几部分组成：液力变矩器、DNR离合器、主动锥盘、金属带、从动锥盘、主减速齿轮、差速器、液压系统、控制系统。变速器的变速原理是液压系统提供的压力改变主从锥盘的工作半径，从而改变速比。下面建立该变速器的锥盘推力模型。

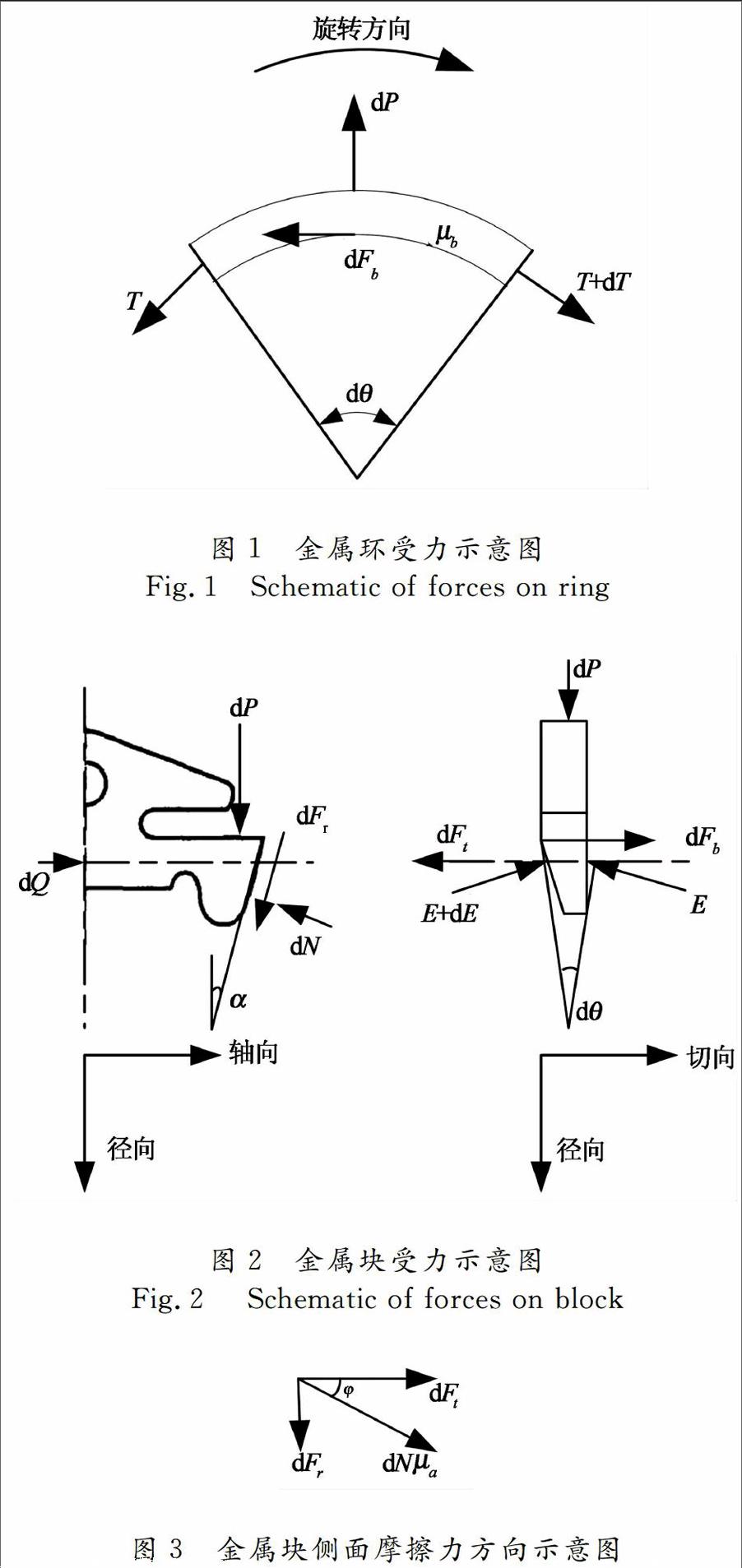
图1～3中各符号意义如下：

P-金属环与金属片径向相互挤压力；

T-金属环的张力；

Q-轴向推力；

N-金属片侧面正压力；

E-金属片之间的挤压力；

F_r-锥轮对金属片的摩擦力（平行锥面向下）；

F_b-金属环对金属片的切向摩擦力；

F_t-锥轮对金属片的切向摩擦力；

μ_a-锥盘与金属片之间的摩擦系数；

μ_b-金属环与金属片之间的摩擦系数；

α-金属片工作面与轴线的夹角，等于11°；

φ-N_μa与F_t的夹角；

θ-主动锥轮或从动锥盘工作包角。

金属块受力如图2与图3所示，图中是从动轮侧金属片。式（17）～（19）中，θ_P与θ_S分别是主动锥轮与从动锥轮的包角，D，d分别是主动锥轮与从动锥轮的工作直径，C是两锥轮的中心距，i是速比。结合金属带的长度，通过几何计算得到主从动轮工作半径D/2，d/2与速比i的关系f_D（i）与f_d（i），其计算公式见式（20）与式（21），两者示意图见图5。

结合式（22）与式（23），主从锥轮的推力比关系式（16）可以描述为速比i的函数，如式（24）。

2 试验测试

2.1 试验系统与方法

为了研究变速器的锥轮平衡推力，采用自主开发的CVT变速器。为了获得与实际应用吻合的数据，试验变速箱不做任何改动。试验变速箱由如下几大部件组成：油泵、液力变矩器、离合器总成、主从锥轮锥盘、金属带、主减速器、液压阀块。另外，从动缸处有一复位弹簧。变速器的相关参数如表1所示。变速器试验台如图6所示，驱动部分是一台75kW的交流变频电机，负载电机与驱动电机相同，2个转速扭矩传感器，液压系统由比例溢流阀控制系统的压力，即从动缸的压力，另一个比例减压阀控制主动缸的压力，实现速比的控制。试验时，液力变矩器处于锁止状态，离合器一直处于接合状态。

2.2 试验方案

2.2.1 无转矩传递时主动锥轮与从动锥轮的推力比试验

在无输入转矩的工况下，控制主动电机的转速稳定在2000r/min，从动缸的压力稳定在2MPa，控制主动缸的压力，完成2.43～0.44全范围速比稳定试验。完成此从动缸压力下全范围速比稳定试验后，调整从动缸压力分别稳定在3MPa与4MPa，进行同样的试验。

2.2.2 转矩对主从推力比的影响试验

主动电机的转速稳定在2000r/min，输入转矩恒定在60N·m，针对不同速比，调整从动缸的压力，使转矩比恒定在0.5，测量不同速比下的主从推力比。转矩比是指输入转矩与某推力下能承受的最大转矩之比。调整输入转矩恒定在80N·m与100N·m，进行同样的试验。

2.2.3 转矩比对主从推力的影响试验

控制主动电机的转速稳定在2000r/min，调整从动缸的压力使之能传递140N·m的最大转矩，调整主动缸的压力使速比稳定在2。0，输入转矩100N·m，80N·m，60N·m，40N·m，20N·m与0N·m，测量各个转矩下的推力比，同样条件下完成速比分别为1.0与0.5的试验。按上述方法，分别完成最大传递转矩为120N·m，100N·m与80N·m的试验。

2.2.4 主动轮转速对主从推力影响试验

控制主动电机的转速稳定在1000r/min，调整输入转矩为60N·m，转矩比为0.5，控制主动缸的压力，完成速比为2.43～0.44的试验。按同样的方法，完成主动电机转速分别为2000r/min与3000r/min的试验。

2.3 数据计算

变速器的推力计算由式（5）与式（6）可知：

Q=N（cosα+μsinΦsinα）。 （25）

由于α的值等于11°，式（25）后半部分的值远小于前半部分的值，因此把式（25）简化成式（26）。

Q≈N。 （26）

因此，主动锥盘与从动锥盘的推力可描述如下：

Q_P≈P_P×A_P+F_rt（Np）， （27）

Q_S≈P_S×A_S+F_rt（N_S）+F_spr。 （28）式中：Q_P是主动锥盘的推力；P_P是主动缸的压力，A_P是主动缸的面积；F_rt（N_P）是主动缸旋转产生的液压推力；Q_S是从动锥盘的推力；P_S是从动缸的压力；A_S是从动缸的面积；F_rt（N_S）是从动缸旋转产生的液压推力；F_spr是从动缸的弹簧推力。

根据F.M.White的计算，旋转产生的推力与缸的内外半径、油液质量以及转速有关。结合本项目的数据，主从动缸的旋转液压推力计算结果如图7所示。

从动锥盘复位弹簧推力的试验曲线如图8所示。根据上述的计算方法，再结合主动缸与从动缸的压力，可以计算两者的推力Q_P与Q_S。

3 试验结果与分析

3.1 无转矩传递时主从动锥轮推力比试验结果以

及转矩对主从推力比的影响试验结果

如图9，图10与图11所示。图中的理论推力比是假设在全速比范围内主从动锥轮摩擦系数相等的条件下获得的，试验结果与理论公式的计算结果趋势相同。图9是无转矩传递时，不同从动轮压力下得到的主从锥轮推力的试验数据。图10中，在速比0.5～1.0这一区间，试验值大于理论值，而在速比的后段区间，试验值小于理论值，理论公式与试验结果证明了推力比与速比是呈有规律的单调递减的关系，转矩对主从推力比影响的试验结果也证明了这点。图11显示，转矩对推力比的影响比较明显，同一速比下，输入转矩越大，推力比越小。以速比等于1.0时为例，当输入转矩为60N·m时，推力比等于1.51，当输入转矩为100N·m时，推力比等于1.39，两者相差8.6%。Kunio也证实了此现象。这一现象产生的原因可以解释为，因为传递的转矩变化，传动的摩擦系数发生了改变。

3.2 转矩比对主从推力的影响试验结果

在速比等于0.5与1.0的工况下，如图12和图13所示，推力比随着转矩比的增大而呈线性增大，在速比等于2.0的工况下，如图14所示，转矩比小于0.52的区间，推力比随着转矩比的增大而呈线性增大，但在转矩比大于0.52的区间，推力比呈现出稳定的趋势。在三种不同速比的工况下，同一转矩比工况下，最大转矩值越大，推力比越小，但两者相差不大。以速比等于1.0的工况为例，最大转矩是80N·m，推力比等于1.37，最大转矩是140N·m时，推力比等于1.28，两者相差7%。转矩比导致推力比变化的原因，可以解释为传动的摩擦系数发生了变化。如图15所示，在转矩比0.77的工况下，根据式（24），改变主从锥盘的摩擦系数，仿真结果与实测结果完全一致。

3.3 主动轮转速对主从推力比的影响试验结果

如图16所示，在转矩比等于0.77，三个不同转速的工况下，其推力比相差很小，在速比等于1的工况下，1000r/min的推力比等于1.318，3000r/min的推力比等于1.345，两者相差2%。可以认为，主动轮转速对推力比的影响可以忽略。

4 结论

1）建立了无转矩工况下主从推力比的数学模型，针对有转矩输入的工况，根据理论分析与试验数据，为满足工程应用的需要，把推力比定义为摩擦系数与速比的函数Q_P/Q_S=f（μ_a，μ_b，i）。

2）速比对推力比的影响较大，推力比与速比呈有规律的单调递减的关系。

3）根据转矩对推力比试验结果分析可知，转矩对推力比有一定的影响，同一速比下，输入转矩越大，推力比越大，推力比相差约8.6%。推力比随转矩变化的原因是传动时摩擦系数发生了变化。

4）转矩比对推力比影响明显，在速比等于0.5与1.0的工况下，推力比随着转矩比的增大而呈线性增大，在速比等于2.0的工况下，转矩比小于0.52的区间，推力比随着转矩比的增大而呈线性增大，但在转矩比大于0.52的区间，推力比呈现出稳定的趋势。同一转矩比工况下，最大转矩值越大，推力比越小，两者相差约7%。推力比随转矩比变化的原因同样是传动时摩擦系数发生了变化。

5）主动轮转速对推力比的影响可以忽略。