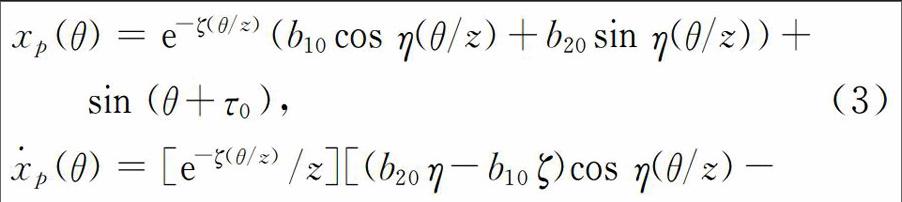振动落砂机系统的拟周期碰撞设计

2016-08-12伍新文桂林何莉萍徐慧东魏克湘

湖南大学学报·自然科学版 2016年4期

伍新　文桂林　何莉萍　徐慧东　魏克湘

摘要：首先建立了落砂机系统周期运动的Poincaré映射，考虑到在设计过程中经典的Neimark_Sacker分岔临界准则需要直接计算特征值带来的局限性，利用不直接依赖于特征值计算的显式临界准则，获得了系统发生Neimark-Sacker分岔的两参数区域图，所获得的参数区域图有助于主动设计系统的拟周期碰撞运动。然后应用中心流形正则形方法进一步分析了拟周期碰撞运动的稳定性。最后数值仿真表明在选定的系统参数处能产生稳定的拟周期碰撞运动。

关键词：落砂机；冲击振动；Neimark-Sacker分岔；拟周期碰撞运动；稳定性

中图分类号：0322；TB123 文献标识码：A

碰撞振动在实际工程领域中普遍存在，由于碰撞和冲击过程中固有的不连续性造成的强非线性，使得系统的动力学响应十分复杂多变，产生丰富的非线性现象，如分岔和混沌现象等。

振动落砂机是一种利用碰撞振动原理对砂箱进行落砂的机械设备。这种周期碰撞的机械设备工作频率单一，导致生产效率低、能耗高。而拟周期碰撞是典型的非线性振动，与简单的周期碰撞相比，拟周期碰撞具有多频性，以及振动加振荡之复式激振品质，可提高系统的功能和效率，同时又没有混沌运动的不可预测性和初始条件敏感性，该特性在实际工程领域具有应用潜力，能有效解决上述存在的一些缺陷。

近来，国内外一些学者对振动落砂机系统非线性特性开展了理论和数值模拟分析。罗冠炜等通过理论分析和数值仿真揭示了振动落砂机周期运动经概周期分岔和倍周期分岔通向混沌的演化过程。丁旺才等使用中心流形范式方法研究了振动落砂机系统在强共振下的两参数开折的局部动力学行为并通过数值仿真进一步揭示了系统共振点附近的Hopf分岔不变环面和次谐分岔4-4周期运动。

随着分岔理论和非线性动力学设计方法的发展，人们开始关注如何主动利用分岔特性来提高系统的功能与效率，通过主动选择系统的参数来设计出具有所期望特性的分岔解。然而上述文献中对振动落砂机系统的非线性现象的研究大部分是基于特征值的特性来描述的传统的分岔准则。对于一个四维多参数的落砂机碰撞振动系统，如果按照传统的Hopf分岔临界准则，逐点试算特征值是否满足分岔的存在条件，这对于通过设计来主动实现分岔解具有一定的局限性。针对传统分岔准则的不足，文桂林等提出了新的离散系统Hopf分岔准则，建立的Hopf分岔准则是由一些系统参数构成的代数等式和不等式组成的显式分岔临界准则，并不依赖于特征值的计算，这更适合分岔参数机理分析和设计。

本文以振动落砂机系统为研究对象，针对传统的映射Hopf分岔临界准则在主动设计方面存在的局限性，基于Neimark-Sacker分岔（二次Hopf分岔）理论，使用不直接依赖于特征值计算的显式临界准则来设计系统的参数，使其产生拟周期碰撞运动。然后，应用中心流形一正则形方法来分析拟周期碰撞运动的稳定性。最后，通过选取适当的系统参数，数值实现了系统稳定的拟周期碰撞运动。

1 力学模型及其运动方程

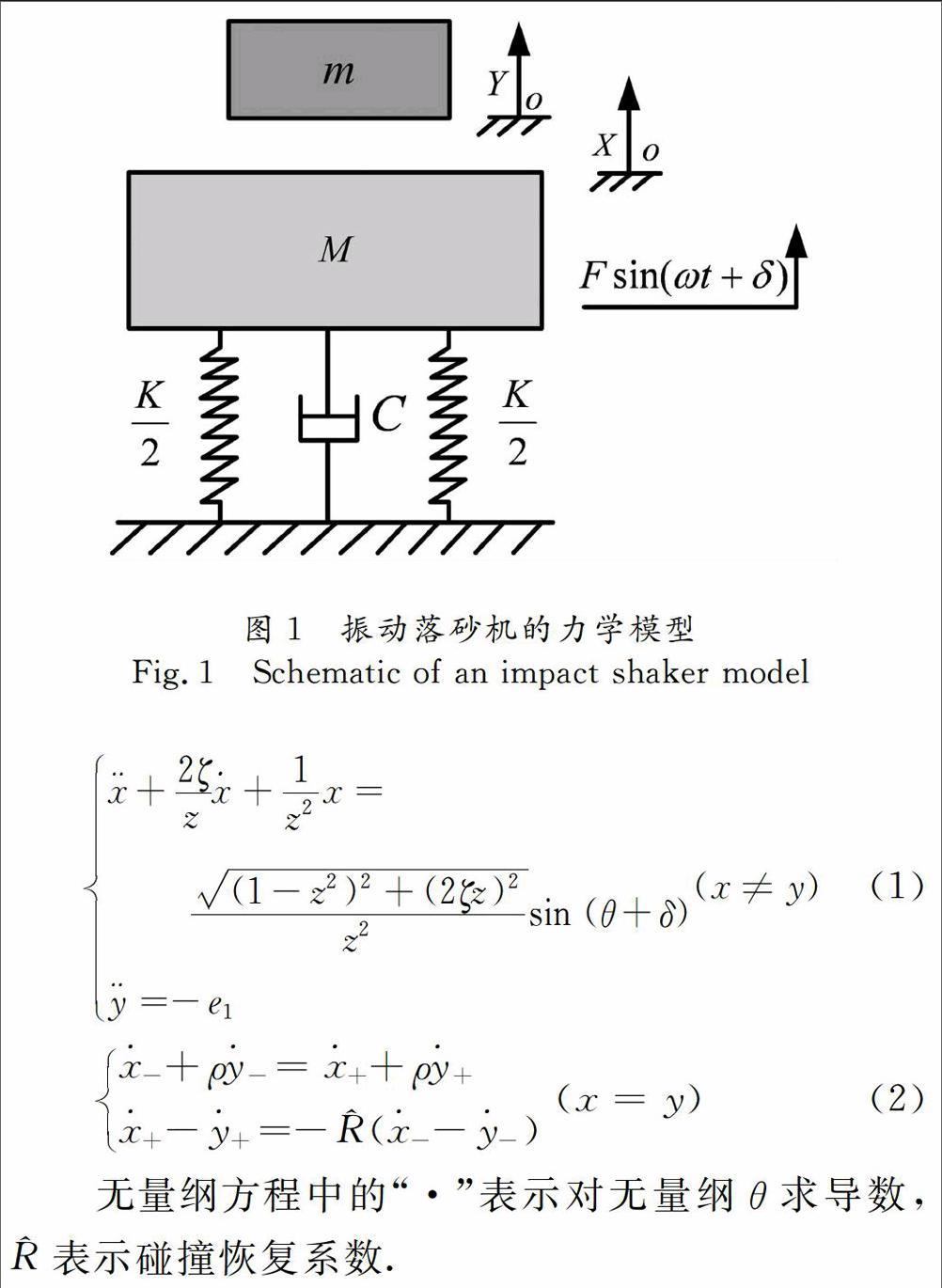
对于振动落砂机系统的设计，仅考虑垂直方向振动，将振动落砂机系统简化为图1所示的两自由度的质量弹簧阻尼器系统。其中，质量块M，m分别表示质量为M的振动基座和质量为m的砂箱（包括型砂和铸件），振动基座和基础之间用刚度为K的线性弹簧和阻尼系数为C的阻尼器连接，振动基座受到简谐力Fsin（ωt+δ）的作用。图中X，Y分别表示基座和砂箱的位移。砂箱和基座不发生碰撞时，砂箱只受重力作用，当基座和砂箱位移相同即X=y，并且相对速度不为零时，它们会发生垂直方向的正碰。为了方便计算，振动落砂机系统采用文献中的无量纲运动微分方程来描述：

无量纲方程中的“·”表示对无量纲θ求导数，R表示碰撞恢复系数。

2 振动落砂机系统周期运动的Poincaré映射

由无量纲方程（1）和（2）可知，在系统未发生碰撞时，基座和砂箱会遵循方程（1）做连续运动。当发生碰撞时，基座和砂箱的速度会遵循冲击方程（2）发生突变，得到下一次做连续运动的初始值，因此系统会进行碰撞、连续运动、再碰撞的循环运动。为了使系统产生Neimark-Sacker分岔，求得一个周期冲击运动。其无碰撞部分的解析表达式如下：

3 振动落砂机系统的拟周期碰撞运动

3.1 振动落砂机系统Neimark-Sacker分岔的显式临界条件

为了设计出振动落砂机系统拟周期碰撞运动，主要任务就是确定适当的系统参数，使系统（11）发生Neimark-Sacker分岔。如果采用传统的分岔临界准则，需要在参数空间内通过逐点取值来计算和验证系统的特征值是否满足Neimark-Sacker分岔的临界准则，这种数值搜寻的方法具有一定的盲目性和不确定性，非常耗时。另外，虽然可以采用极点配置方法找到满足特征值分布条件的系统参数点，但该方法也是先确定特征值后再确定参数，确定的参数对于系统仍存在机理不明确问题。特别是对于横截条件，由于需要求特征值对分岔参数的导数，极点配置方法无法解决。因此为了克服传统分岔临界准则的局限性，本文采用不直接依赖于特征值计算的映射Neimark-Sacker分岔的显式临界条件来获得系统参数。

设映射（11）的一个不动点为X^*=（x^*，x^*，y^*，τ^*）^T，在不动点处映射（11）的线性化矩阵的特征多项式为：

这里选取μ=（ρ，β），a_i=a_i（ρ，β）是与分岔参数ρ和β有关的实数，i=1，…，4。针对建立的振动落砂机系统周期运动的Poincaré映射（11），有如下的引理。其中条件（Ⅰ）保证有一对复共轭特征值位于单位圆上；条件（Ⅱ）保证其它的特征值位于单位圆内；条件（Ⅲ）保证映射不动点是合理存在的；条件（Ⅳ）保证在参数扰动下，位于单位圆上的特征值穿越单位圆的速度不为零；条件（Ⅴ）保证Neimark-Sacker分岔是非共振的。

3.2 振动落砂机系统Neimark-Sacker分岔的存在性

选取落砂机系统的参数ζ=0.2，R=0.85，z=2.8，以ρ和β为分岔参数（即μ=（ρ，β））。在（ρ，β）张成的一个二维的参数空间内，根据引理1中的显式条件，利用Maple软件得到如图2所示的两参数分岔图。

图2中白色区域Ⅰ和Ⅱ内的点都满足引理1的条件（Ⅱ）-（Ⅲ）中的不等式，但在灰色区域Ⅲ和Ⅳ中至少有一个条件（Ⅱ）和（Ⅲ）中的不等式不成立。由曲线EA，AB，BC，CD和DE围成的白色区域工除了满足条件（Ⅱ）-（Ⅲ）还满足△>0，因此白色区域工为系统周期运动的稳定参数区域。曲线DE是由临界条件（Ⅰ）中的△=0得到，曲线DE上由条件（Ⅴ）得到的点R₃和R₄分别为系统出现3阶和4阶强共振点。点划线l和m由横截条件（Ⅳ）不等式左边的表达式取等号得到的，这样两曲线l和m和曲线DE的交点T₁和T₂不满足Neimark-Sacker分岔的横截条件（Ⅳ）。由此在选取系统参数临界点时应该避开这些强共振点和非横截点。在由曲线DE，EF，FG和GD围成的白色区域Ⅱ内，在曲线DE的附近是出现系统拟周期碰撞运动的潜在区域。为了分析分岔解的稳定性，在分岔图的白色区域内的Neimark-Sacker分岔临界曲线DE上任取一点μ₀=（ρ₀，β₀）=（0.6，0.95441）作为临界分岔值。

3.3 振动落砂机系统拟周期碰撞运动的稳定性

振动落砂机系统出现的拟周期碰撞运动的稳定性，也即Neimark-Sacker分岔解（不变圈）的稳定性取决于映射（11）的非线性项。采用中心流形范式方法或者频域方法都可以分析Neimark-Sacker分岔的稳定性。本文使用投影法来分析分岔的稳定性。

取坐标变换（13）式中的X^*为映射（11）的不动点，μ₀为临界分岔参数值。

映射（11）经过坐标变换（13）变换成

则通过变量变换后的新映射（14）的不动点和分岔点都转化为了零点。这样映射（11）发生Neimark-Sacker分岔后产生的拟周期碰撞运动的稳定性可由引理2来确定。

引理2 如果在临界分岔值μ=μ₀处，映射（14）的雅克比矩阵在分岔点v=0处有一对复共轭特征值λ₁（v）和λ₂（v）满足|λ₁（0）|=|λ₂（0）|=1和横截条件λⁿ₁（0）≠1，N=3，4，并且d|λ₁（N）|/dv|_v=0≠0，而其它的特征值|λ_j（0）|<1，j=3，4，那么在v=0，当α（0）<0（或α（0）>0）时，从X^*（po）分岔出稳定的（不稳定的）Hopf不变圈。其中，α（0）参见下列表达式：

根据（15）和（16），在μ=μ₀计算得到

α（0）=-0.089<0。

因此，根据引理2可判断系统会产生一个稳定的Neimark-Sacker分岔解，即系统稳定的拟周期碰撞运动。

3.4 数值实验

为了验证上述理论分析和研究振动落砂机系统在分岔点附近的动力学行为，其它三个参数不变，临界参数100不变，变化分岔参数β，在落砂机的分岔临界点附近设置了6组参数扰动值，并做了相应的数值仿真，文中的数值仿真都采用4000次碰撞。在Poincaré映射分岔图的白色区域Ⅰ内的分岔临界曲线DE附近取一组分岔参数μ=μ₀+△μ=（ρ₀，β₀-0.02），其中△μ是临界参数扰动量，设置映射初始值X=X^*+△X，其中△X=（0，0，0，0.001）^T为不动点扰动量，在该参数点处系统处于稳定的周期运动，即Poincaré映射上一个不动点，如图3（a）所示。在Poincaré映射分岔图的白色区域Ⅱ内并且充分接近曲线DE的参数区域内取分岔参数μ=（ρ₀，β₀+00004），在该参数点处系统处于稳定的拟周期碰撞运动，即Poincaré映射上一个不变圈，如图3（b）所示。继续变化分岔参数值，当取分岔参数μ=（ρ₀，β₀+0.0456）时，拟周期运动失稳，产生锁相运动，如图3（c）所示。当取参数μ=（ρ₀，β₀+0.046）时系统退出锁相运动，又产生拟周期吸引不变圈，如图3（d）所示。当取控制参数μ=（ρ₀，β₀+001）时系统产生拟周期吸引不变圈，不变圈幅值更大，如图3（e）所示。当继续扰动参数值至μ=（ρ₀，β₀+0.22）时系统经锁相转迁为混沌运动，如图3（f）所示。通过以上仿真分析，振动落砂机系统展示出了丰富的动力学行为，在Hopf分岔临界点附近作参数扰动，当参数扰动量足够小的时候由Hopf分岔所产生的不变圈在形状上类似于一个椭圆。随着参数扰动量的增大，不变圈不断增大，其形状也变得越来越不规则。仿真显示只有当系统的扰动参数很大时才发生混沌，说明系统的拟周期碰撞运动具有强的鲁棒性和较大的稳定域。因此，在设计系统参数时，在白色区域Ⅱ邻域内靠近分岔临界曲线DE处取系统参数可以产生稳定的拟周期碰撞运动。