直流逆变分布式电源降阶模型及小扰动稳定分析

李培强　胡泽　李欣然　周丽英　曾小军　邱时严

摘要：分布式电源类型及控制方式多样，致使含多种分布式电源的小扰动机电暂态分析的电网模型复杂，分析难度加大。针对应用较广的光伏和燃料电池两种分布式电源，在对其全阶状态空间模型的特征分析和电池动特性时间尺度分析的基础上，提出了前馈解耦控制下考虑电池U-I外特性和逆变控制系统动特性的光伏发电系统降阶模型和忽略逆变系统快动态特性的燃料电池降阶模型，并应用于4机2区域系统并网小扰动分析。研究结果表明：直流DG并网主要通过改变系统潮流及平衡点影响系统阻尼特性；直流DG出力增加时，与采用降低出力增加旋转备用运行方式的常规机组强相关的模式阻尼特性会呈现增大的趋势。

关键词：固体氧化物燃料电池；光伏发电；降阶模型；特征模式；小扰动稳定

中图分类号：TM711 文献标识码：A

分布式电源（DistributedGeneration）作为一种新能源发电技术，近年来取得了快速的发展。它既可并网发电运行也可微网独立供电，因此在地区电网中得到了广泛的应用。其中包括逆变接口并网的直流分布式电源：光伏发电和燃料电池。逆变接口虽然使DG运行和控制更加灵活，但当系统受扰时，其系统惯量较小因而也更易引发振荡失稳。

对于光伏发电、燃料电池发电、风电等并网对系统稳定性影响分析，国内外学者进行了大量研究，并取得了丰富的成果。文献利用特征值分析的方法，从风机分类，模型简化，并网容量，接入地点，影响机理等各个方面细致地研究了风电并网小扰动稳定问题，得到了一系列有益的结论。然而现有针对逆变接口DG的小扰动稳定分析中，并未考虑电池时间尺度与网络时间尺度匹配的问题，大都采取基于网络方程、负荷模型、并网接口模型、各控制方法的全系统高阶模型，其阶数较高因而很难用于大规模系统。文献对含同步发电机接口和逆变器接口模型的微网进行小信号建模，其阶数高达29阶，单个逆变器模型也有13阶。文献忽略了内环快动态，对逆变接口进行降阶处理，但其同样是微分方程描述的高阶系统。此外，以光伏发电为代表的大规模无转动惯量电源接入改变了系统潮流分布，减小了系统等效转动惯量，其对系统小扰动稳定性的影响值得研究。文献以光伏发电接入IEEE14节点为例，分析了规模化光伏并网对系统阻尼特性的影响，并认为光伏发电并网增强了系统阻尼。文献利用含SOFC的扩展P-H模型分析了燃料电池并网对系统机电振荡模式的影响，但却并未在大系统中验证。

针对上述问题，本文从系统的角度出发，分析光伏（PV）和固体燃料电池（SOFC）的电池特性，采用前馈解耦的控制方式，建立了考虑各重要环节的详细状态空问模型，通过分析系统特征模式及电池动态时间尺度，忽略SOFC并网系统快动态，实现了模型降阶，建立了直流DG降阶模型，并对其接人弱耦合两区域算例进行了仿真，以此分析了直流DG并网对系统阻尼特性的影响。

1 直流DG状态空间模型

1.1 电池模型

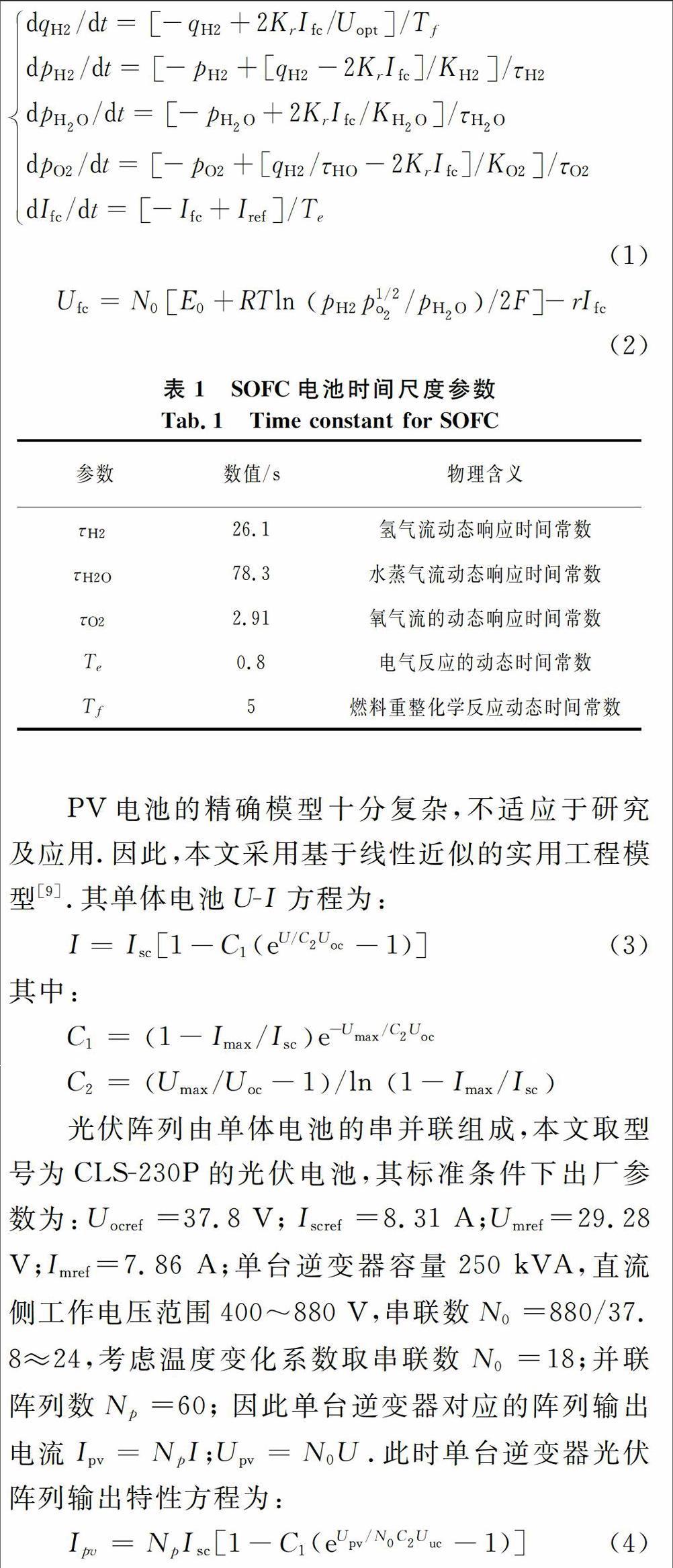
为实现基于系统线性化动态微分代数（DAE）方程组的小扰动分析，需将由电池阵列、DC/AC逆变电路、并网控制电路等模块构成的系统数学模型线性化。其中SOFC堆电池作为一个受控电压源，其动态微分方程及输出U-I方程如式（1）（2）所示，各时间尺度参数如表1所示，其他参数说明见文献。

PV电池的精确模型十分复杂，不适应于研究及应用。因此，本文采用基于线性近似的实用工程模型。其单体电池U-I方程为：

光伏阵列由单体电池的串并联组成，本文取型号为CLS-230P的光伏电池，其标准条件下出厂参数为：U_ocref=37.8V；I_scref=8.31A；U_mref=29.28V；I_mref=7.86A；单台逆变器容量250kVA，直流侧工作电压范围400～880V，串联数N₀=880/37。8≈24，考虑温度变化系数取串联数N₀=18；并联阵列数N_p=60；因此单台逆变器对应的阵列输出电流，I_pv=N_pI；U_pv=N₀U。此时单台逆变器光伏阵列输出特性方程为：

非标准条件下的参数开路电压U_oc，短路电流I_sc及最大功率点电流I_m，电压U_m可通过下式得到：式中：T_air为空气温度；k为温度系数，通常取0.03℃·m²/w；e为自然对数；a，b，c为补偿系数，其值分别为0.0025℃，0.5m²/W，0.00288℃。

1.2 直流侧电容动特性

假定忽略各开关管损耗，则直流DG输出功率等于逆变器输出功率与直流侧电容增加的功率之和。参考方向如图1所示，由此可得直流稳压电容的状态方程如下：

C_dcdU_dc/dt=I-3U_sddI_d/2Ud_dc （6）式中：C_dc为直流稳压电容；I为直流DG输出电流。

1.3 逆变器及控制系统模型

并网系统通常包括稳压电路、逆变电路以及控制回路，并网等效电气图如图1所示。采用d轴定向法，将d-q坐标系的d轴定向与并网节点，则有U_sq=0，并通过派克变换得到同步旋转dq坐标系下数学模型如下：式中：ω为交流系统基波角频率；U_sd，U_sq分别为交流侧并网节点电压矢量的d，q轴分量；I_d，I_q分别为交流侧系统电流矢量的d，g轴分量；S_d，S_q为三相逆变器开关函数的d，q轴分量，R为线路和开关管等值电阻，L为线路及变压器等值电感。

三相逆变器采用前馈解耦的控制策略，且为实现单位功率因数并网，一般控制无功电流为零，如图2所示。PV由于光照强度等的间歇性，一般工作于最大功率点模式，本文利用导纳增量法追踪最大功率点处电压U_m作为直流侧电压参考值U_dcref，电压差值通过PI调节得到电流内环的参考值，电流差值通过PI调节得到等效控制变量U_dr，U_qr，然后通过引入电压前馈补偿和电流状态反馈获得逆变器控制电压在dq坐标系的参考值U_d，U_q，即s_dU_dc，s_qU_dc。为建立适用于小扰动分析的状态空间模型，引人中间变量U_dcr，I_dr，I_qr，并通过拉普拉斯反变换得到控制方程如下：

对于SOFC，其功率输出直接由需求决定，因此一般采用PQ控制策略，相对于PV而言只需将直流电压外环替换为有功功率外环即可。通过上述分析，即可消除时变的开关函数的影响，将三相换流器动态方程转化为线性微分方程，使基于状态方程的特征分析成为可能。其中k_p，k_i，k_p^*，k_i^*分别为电流内环和功率外环的PI参数。

2 直流DG发电系统特征分析

2.1 直流DG接入强耦合无穷大系统算例

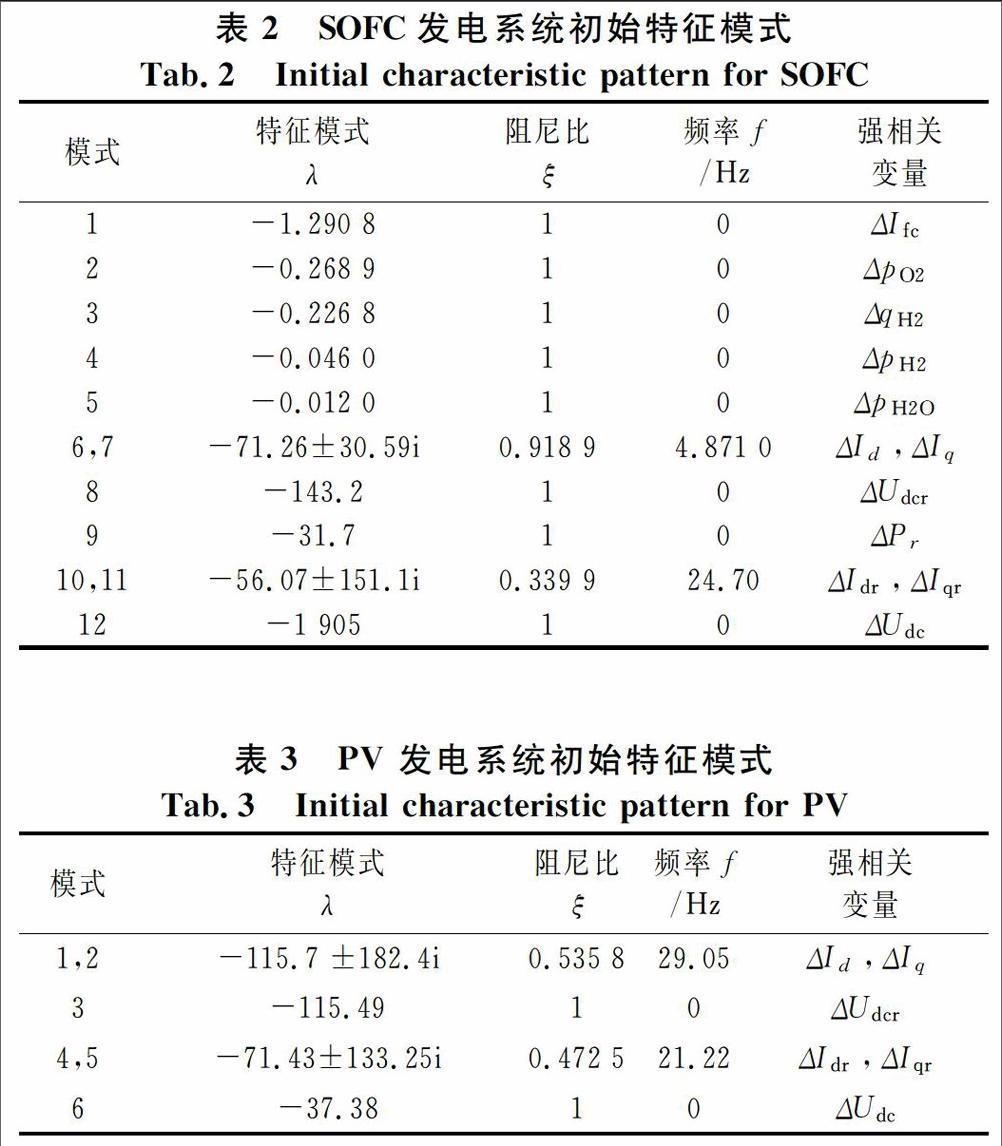
本文采用PV和SOFC发电系统接人强耦合系统作为算例，其电气接线图如图1所示，单台逆变器容量S_B=250kVA，归算到S_B下的参数为：L=0.0035pu，R=0.012pu，C_dc=0.0038pu。光伏系统初值S=750W/m²，T=25℃，k_p=0.5，k_i=80s^-1，k_i^*=0.9，k_i^*=50s^-1；SOFC工作温度1273K，k_p=0.5，k_i=30s^-1，k_p^*=1，k_i^*=100s^-1。接人强耦合系统，可用无穷大母线表示。由于系统中无同步机及动态负荷，可直接分析直流DG发电系统本身的特征模式。通过计算系统各衰减模式的参与因子，衰减振荡模式的频率及阻尼，可找出与各模式强相关的状态变量，并分析振荡模式的性质。如表2～3所示。

由表2可知：初始平衡点处SOFC系统共有12个特征模式，其中与SOFC堆动态特性强相关的均为衰减模式，且衰减速率较慢。这是由SOFC堆动态时间常数及系统惯量较大，动态特性缓慢所引起的。分析式（1）及模式1～5参与因子可知，SOFC堆动态特性方程是与平衡点无关的常系数线性微分方程，其特征模式仅与本身的变量相关。而与逆变器及控制变量强相关的模式，其衰减特性均较快，这是由并网逆变器及控制器的高频动态特性所决定。

由表3可知：初始平衡点处PV发电系统共有6个特征模式，均为衰减模式，且与逆变器及控制变量强相关，两对衰减振荡模式频率较大且阻尼特性良好，但与△U_dc强相关的模式差异很大，分析式（2）（4）（5）可知，这是由SOFC及PV电池堆的U-I特性方程不一致所引起。

2.2 参数特征值轨迹

以下以光伏发电系统为例，分析控制参数对系统稳定性影响。令T=k_p/k_i，T^*=k_p^*/k_i^*，控制系统参数变化时特征值轨迹如图3所示。

由图3（a）（b）可知：内外环比例系数增大，系统主特征模式朝负半平面的稳定区域移动，对应系统稳定性增强，稳定裕度提升；外环比例系数增大时，模式4，5不变。对比图3（c）（d）可知：内外环积分系数增大，模式1，2虚部增大，模式3，6相互靠近；外环积分系数增大时，模式4，5不变，而内环积分系数增大时，模式4，5由衰减模式转化为振荡模式。综上可知，模式4，5的性质主要受到内环参数的影响，适当的增大比例系数可增强系统稳定性，而积分系数过小时，部分模式实部接近正半平面，系统稳定性变差。因此，为维持系统受扰暂态性能需合理地选择控制系统参数。

2.3 小扰动非线性仿真

本文在matlab/simulink中建立了拓扑如图1所示的光伏与燃料电池发电系统仿真模型，并通过设置扰动观测电池与逆变控制系统小扰动下动态特性。

图4为在0.4s时光照强度由750W/m²阶跃上升至1000W/m²，在0.8s时阶跃下降至800W/m²时，逆变器出口电流I_d，I_q的仿真曲线，可以看出受扰暂态过程为衰减的振荡过程，光伏发电系统小扰动稳定，这与理论分析以及文献结果一致。

图5分别为3.5s时有功指令由1阶跃至1.1，5s时母线电压跌落10%，5.5s恢复时，SOFC内氢气、氧气和水的分压P_H2，P_O2，P_H2O和有功功率P的受扰响应曲线。可见，由于p_H2，p_O2，p_H2O的响应时间常数较大，其在暂态过程中衰减速度较慢，因此在受扰暂态过程中可以认为其基本不变，从而忽略其动特性，直接作为一个受控电压源处理。同时，由表1可知电池的输出电流I_fc的电气响应时间常数T_e为0.8s，远大于逆变控制系统的快动态特性，因此在受扰暂态中快动态特征模式不会被激发。

2.4 直流DG发电系统机电暂态降阶模型

由上节分析可知，在小扰动过程中，光伏电池无动态响应时间常数，系统的主特征模式主要受电池U-I外特性和逆变器及控制系统影响，因此其逆变控制系统快动态必须考虑，由此可推导得以DAE方程组描述的光伏发电系统降阶模型如式（4）（6）（7）（8）；SOFC电池动特性缓慢，时间尺度远大于逆变控制系统快动态，受扰暂态中快动态特征模式不会被激发，机电暂态仿真中逆变控制系统的快动态可忽略。同时，考虑到SOFC输出受扰暂态行为受到母线电压这一唯一的交流侧电气量的影响，将控制系统内外环简化为一个一阶动态环节，推导可得SOFC发电系统机电暂态降阶模型如下：式中：T_d，T_q分别为有功、无功一阶环节时间常数；P_ref，Q_ref分别为有功、无功指令值；U_sref，U_s分别为母线电压稳态值和运行值。

3 直流DG并网小扰动分析

3.1 仿真系统及其参数

以光伏发电系统为例，分析直流DG并网对系统机电模式的影响。与风电场类似，在机电暂态仿真中，考虑站级直流DG的各部分详细模型过于复杂且没有必要。针对本文的研究重点，假设电池组中各单体工作状态相同而忽略成组不一致性问题，将电池串并联等效为大型的电池阵列；忽略电站内部集电系统损耗，利用倍乘等值的方法，将并联发电单元等值为单一模型。系统接线图如图6所示，系统由两个对称的区域组成，每个区域各有两个容量为900MVA的同步发电机，负荷采用静态ZIP负荷。区域1与区域2负荷分别为967MW和1767MW，区域1通过弱联络线向区域2送电约400MW。系统基值S_B=100MVA，在实际运行中，DG更多的是接人新节点，而不是取代同步机运行，因此本文将DG通过升压变压器接入送端母线6，改变DG出力（以DG出力占系统总输出的百分比表示），并分别通过调整送端区域1和受端区域2机组出力来维持负荷平衡。

3.2 分析与讨论

表4反映了DG出力增加时减小送端机组G2出力维持负荷平衡情况下，系统的振荡模式。其中模式1，模式2，模式3分别与G2，G4，G3的功角△δ和转子角速度△ω强相关。由表可知：DG出力增加，送端机组减小出力，模式1的阻尼呈增大的趋势，模式2，3的阻尼呈减小的趋势。

表5反映了DG出力增加时减小受端机组G4出力维持负荷平衡时系统模式。此时，DG出力增加，模式1阻尼基本保持不变，模式2阻尼呈增大的趋势，而与平衡机强相关的模式3阻尼则先增大后减小。可知，DG出力增加时，系统通过调节同步机出力来维持负荷平衡，系统潮流改变，同步机的运行模式变化，由此引起系统阻尼特性的变化，此时并未出现与直流DG强相关的局部模式。系统的阻尼特性整体变化不大，但与出力减小的常规机组强相关的模式阻尼特性会呈现增大的趋势。

由上分析可得如下结论：

1）直流DG并不直接参与系统的机电振荡，而是通过改变系统潮流分布及系统平衡点，从而改变系统阻尼特性。

2）直流DG渗透率增加时，对系统的机电振荡模式影响不大，但与出力减小的常规机组强相关的模式阻尼特性会呈现增大的趋势，这是由于DG出力增加时，为维持系统负荷平衡，同步机出力减小，系统旋转备用增加，与其强相关的模式阻尼特性会升高，这也与传统分析中，同步机出力越小，越远离稳定极限，系统稳定性变强的结论一致。

3）由于逆变接口DG通过前馈解耦实现了与电网的柔性连接，机电暂态过程中仅有母线电压这一唯一的交流量影响DG暂态行为，并网过程中并未出现同步机组与直流DG之间的局部振荡模式。

4 结语

本文针对光伏和燃料电池，首先建立了考虑电池动特性及并网电路动态特性的详细状态空间模型，分析系统特征模式及电池时间常数发现，燃料电池动特性缓慢，致使机电暂态中逆变控制系统的快动态无法激发。光伏电池无动态响应时间常数，系统的主特征模式受电池U-I外特性和逆变控制系统影响，由此提出了考虑电池U-I特性和逆变控制系统动特性的光伏系统降阶模型和忽略逆变控制系统快动态的燃料电池降阶模型。最后将其应用于并网小扰动分析，仿真表明：直流DG并网主要通过改变系统潮流及平衡点影响系统阻尼特性；直流DG出力增加时，与采用降低出力增加旋转备用运行方式的常规机组强相关的模式阻尼特性会呈现增大的趋势。