我国股指期货市场价量关系
——基于分位数回归模型的实证研究
2016-08-11杨双会
杨双会
(福建江夏学院金融学院,福建福州,350108)
我国股指期货市场价量关系
——基于分位数回归模型的实证研究
杨双会
(福建江夏学院金融学院,福建福州,350108)
基于混合分布假说理论,采用分位数回归方法对沪深300股指期货价量关系进行分阶段深层次剖析。结果显示:股指期货市场收益率与成交量之间呈正相关关系,即存在“价量齐扬”和“量缩利减”的现象,且跌停板附近的价跌量涨效应弱于在涨停板附近的价量齐扬效应;第二阶段的收益率和成交量的分位数回归系数波动较大,意味着第二阶段的市场风险大于第一阶段;收益率与成交量总体上呈现动态正相关关系,但成交量在价格上涨和下跌时的变化不稳定,具有明显的不对称性。这反映出我国股指期货市场较强的投机性,因此有必要通过各种方法进一步提高期货市场的运行效率,充分发挥期货市场的功能。
股指期货;价量关系;分位数回归
金融资产的供需关系是通过交易实现的,价格是引导交易机制完成的指标之一,价格的变动反映市场对新信息的反应。在金融资产交易的动态过程中,投资者通过成交量来表达对价格的不同意见,成交量反映投资者对新信息认同差异的程度。同时,作为一段时间内资产交易数量的技术指标,成交量变化会受到市场上各种因素的影响,反映出很多潜在信息。我国沪深300指数期货于2010年4月16日在金融期货交易所上市,其标的物是沪深300指数,合约乘数为每点300元,合约月份分为当月、下月及随后两个季月。由于上市时间不长,我国沪深300指数期货与发达国家的股指期货相比还不够成熟、完善。学术界已有研究多是基于仿真数据,具有局限性。因此,本文基于我国股指期货推出后这5年以来的真实交易数据,研究价量之间的动态关系,以揭示我国股指期货市场的内部特征。
一、文献综述
国外很多学者采用不同的模型和方法对期货市场和证券市场价量之间的关系进行研究,观点主要分为三类。第一类是认为收益率与成交量之间存在正相关关系,即“价量齐扬”和“价跌量缩”。Clark对棉花期货的日收盘数据进行实证研究,发现价格变动的绝对值与价格波动性都与成交量存在着正相关关系。[1]135Epps等根据“混合分布假说”所提出的模型指出价格上涨时的成交量大于价格下跌时,价格变动与成交量成正相关。[2]Board等发现期货价格波动与成交量呈显著正相关关系,成交量是影响价格波动的主要原因。[3]Tauchen and Pitts以及Cormell的研究发现价格波动与成交量之间存在正相关关系。[4,5]第二类是认为收益率绝对值与成交量之间存在正相关关系,即“价量齐涨”和“价跌量涨”。Copeland提出“信息顺序到达模型”,指出价格变动的绝对值与成交量呈正相关。[6]第三类是认为价格波动与成交量之间不存在相关关系。McCarthy and Najand对外汇期货市场上价格波动与成交量之间的关系进行研究,[7]Kocagil and Shachmurove对16个期货品种量价关系进行研究,发现期货价格波动与成交量之间不存在相关关系,而是存在双向因果关系,即期货价格波动能引起成交量的变化,成交量的变化能引起期货价格的波动。[8]
我国部分学者对商品期货的价量关系进行的实证研究则大多是基于混合分布假说理论。陈星采用分位数回归分析上海期货市场及伦敦期货市场收益率和成交量之间的关系,实证结果发现两地期市的量价关系不同:伦敦期货市场的量价关系并不明显;上海期铜呈现“量价齐扬”以及“价跌量亦涨”的现象;上海期铝只呈现“量价齐扬”的现象,价跌时量价关系不明显;上海金属期货市场的收益率与成交量呈现非对称的“V”字型关系。进一步的分析表明,两市场量价关系的差异是由于投资者结构不同。[9]陈晓杰和黄志刚采用微观面板数据计量模型与宏观趋势波段两种方法分析台湾加权指数期货量价关系,发现其价、量之间以及价格波动与成交量之间都存在正向关系,符合主流MDH理论,并表明技术分析在一定程度上有效,大陆投资者在沪深300股指期货上可以参考、借鉴台湾地区的经验。[10]李丹和蔡义杰采用分位数回归方法对上海期货市场铜、铝和燃料油期货收益及波动与成交量的动态关系进行实证研究,结果显示:上海期货市场期货价格收益具有异方差的特点,并且存在量价齐扬和量价背离现象,收益波动和成交量之间随着波动增大呈现逐渐加强的正向关系,从而说明我国期货市场信息传播符合混合分布假说。[11]
综上所述,国内期货市场价量关系研究对象集中在商品期货,研究股指期货的很少,而且多数只考察变量之间的“平均”相关程度或者关系。为了避免研究对象与研究方法的局限性,本文采用分位数回归(Quantile Regression)方法对我国股指期货的价量关系进行研究。
二、混合分布假说量价关系理论及分位数回归研究方法
(一)混合分布假说量价关系理论
Clark在1973年最早提出的混合分布假设(The Mixture of Distributions Hypothesis,MDH)是研究价格波动以及反映市场信息流的理论基础。[1]140该理论认为每日价格的变动可看作是日内价格变动的总和,信息到达速率的递增函数是价格变动的条件,而成交量正是信息到达速率的增函数,价格波动与成交量是由潜在信息流共同决定的,信息流的冲击将同时产生价格和成交量的波动。信息流是一个混合变量,而且无法预测,因此成交量可以作为信息流的替代指标解释波动的持续性和聚集效应。价格变动的绝对值以及价格变动均值与成交量之间存在正相关关系。
传统的金融理论对收益的分布假设一般是正态分布,然而金融数据多呈现尖峰厚尾的特征,所以不能很好地拟合。混合分布假说假定信息流驱动交易量和价格的变化,交易量和收益率序列由一系列的分布构成,可以很好地拟合金融数据。
在混合分布假说的理论框架下,日收益率?以及日成交量?分别表示为:
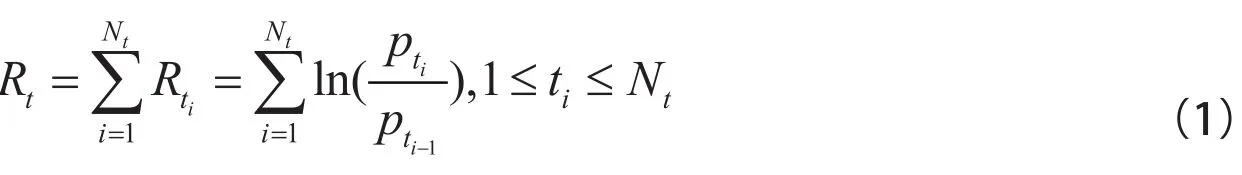

其中,随机变量?是潜在混合变量,表示每天流入市场的相关信息量,反映信息流入市场的速度。?和?分别表示在第天第次信息冲击后形成的均衡成交量和价格。
在一定条件下可以推导出日收益率在大样本下服从均值为0的正态分布:

成交量在大样本下符合泊松分布:

基于上述假设,成交量与收益率的条件方差存在正向关系:

(二)分位数回归研究方法
分位数回归(Quantile Regression,QR)由Koenker和Bassett于1978年提出,该方法可以根据不同的分位点充分利用数据含有的信息对模型进行回归。[12]分位数回归是继最小二乘回归后最受关注的一种方法,它可以使用不同分位函数估计整体模型,是一种更加全面的数据分析方法。相比普通最小二乘估计,分位数回归不但更能精确地描述解释变量?对于被解释变量?的变化范围以及条件分布形状的影响,而且能够捕捉分布的尾部特征。当解释变量对不同部分的被解释变量的分布产生不同的影响时,例如出现左偏或右偏的情况时,它能更加全面的刻画分布的特征,从而得到全面的分析,比OLS回归系数估计更稳健。
三、数据处理及基本统计量分析
沪深300股指期货从推出到现在经历了上升、下降、再上升、再下降的完整周期,本文选取的数据为股指期货推出后一直到当前的最新数据,并根据股指期货市场发展进展,将其分为两个阶段进行比较研究。相比前人的研究,样本容量更大,数据更完整,研究结论也更有说服力。
根据成交量与价格变化的对称性假说,成交量在价格上涨和下跌过程中的变化是一样的,即成交量与价格的变化程度绝对值有关,而与价格变化的方向无关。为了检验这一假说,根据股指期货上市以来价格上升下降变化的情况,分阶段进行研究。第一个阶段是2010年4月16日—2013年12月31日,这一阶段的特点是股指处于下降调整的过程。第二个阶段是2014年1月1日—2015年12 月23日,这一阶段的特征是股指处于急速上升下降过程,波幅较大。由于沪深300指数期货4个期货合约同时上市,分别为当月、下月、下季以及隔季,其中当月连续股指期货的交易量最大,因此采用当月连续股指期货的交易数据。道氏理论认为,收盘价反映了部分的市场行为,是最重要的价格,因此选用日收盘价作为股指期货价格,用?表示,每日成交量用?表示。剔除周末和法定节假日等非交易时间,第一阶段共898个样本数据,第二阶段共483个样本数据,数据来源于通达信。
为了消除时间序列数据可能存在的异方差性,股指期货价格与成交量均取对数,每日收盘价对数,前后两期相减表示收益率。成交量直接取对数。记为:


(一)描述统计
样本数据描述性统计结果见表1:
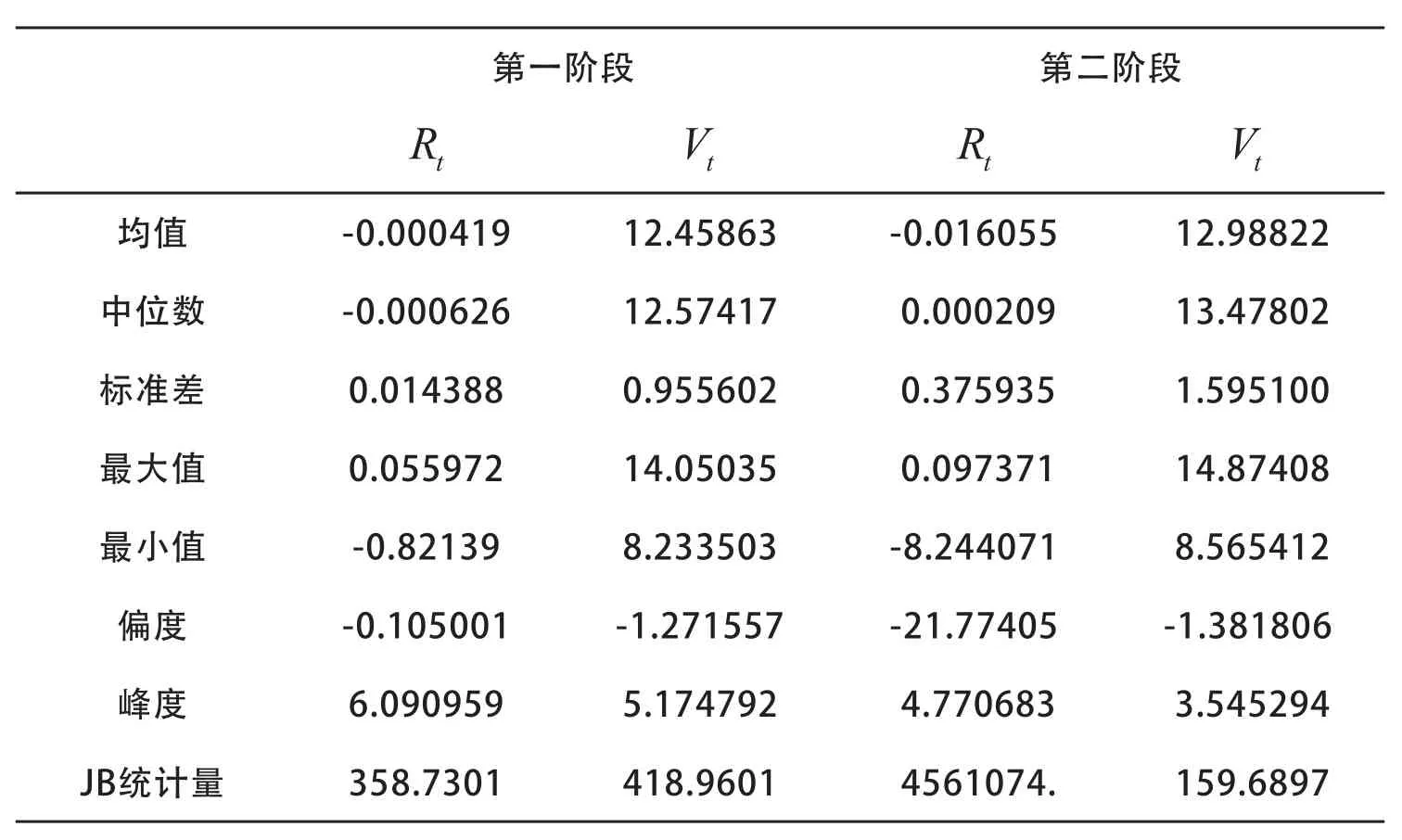
表1 股指期货样本数据序列的描述性统计
由表1可知,第一阶段和第二阶段的收益率与成交量的偏度均小于0,说明收益率与成交量的概率密度函数均呈现明显的左偏特征。两者的峰值均显著大于3,说明呈现明显的尖峰特征。Jarque-Bera统计量的值均很大,因此不能认为样本服从正态分布。
(二)单位根检验
协整分析方法能够揭示变量之间长期稳定的均衡关系,是一种常见的研究各变量之间关系的计量经济方法。在实际操作过程中,需要先对各时间序列进行平稳性检验,因为在协整分析之前,各时间序列或者差分序列需要满足平稳性这一条件。
单位根检验结果中,第一阶段和第二阶段的收益率序列以及其一阶差分都不存在单位根,是平稳序列,而第一阶段成交量序列也不存在单位根,为平稳序列,第二阶段的成交量至少存在一个单位根,不平稳,但其一阶差分序列不存在单位根,是平稳序列,所以第二阶段成交量属于一阶单整序列。
四、建模与估计
以收益率为被解释变量,成交量为解释变量,建立如下价量关系模型:


其中,因变量为收益率,自变量为成交量表示分位数,分位数。为了显示最大涨跌幅限制对股指期货市场的影响,也对尾部和分位数进行回归。不同分位数下的回归系数估计量常常不同,即解释变量对不同水平被解释变量的影响不同。估计结果见表2和表3:

表2 第一、第二阶段收益率与成交量最小二乘回归估计的结果
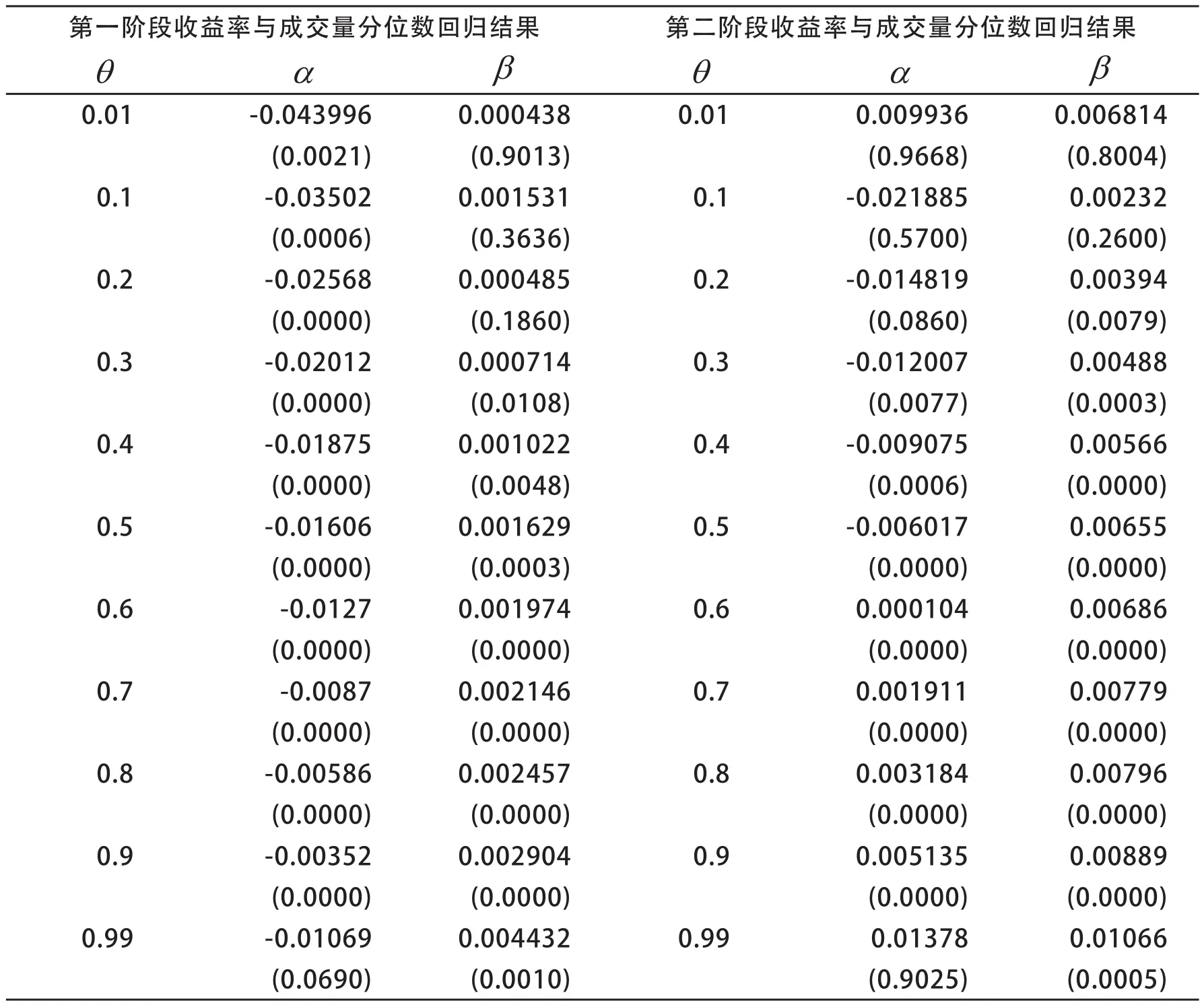
表3 第一、第二阶段收益率与成交量分位数回归估计结果
两个阶段的分位数回归系数见图1和图2:
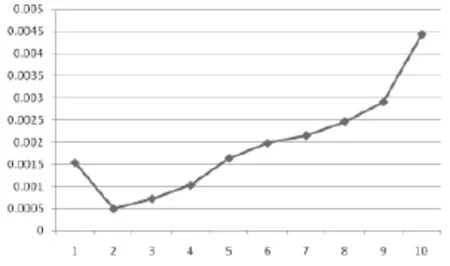
图1 第一阶段分位数回归系数图
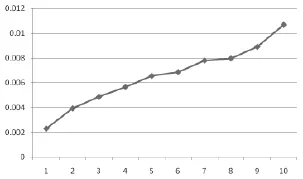
图2 第二阶段分位数回归系数图
(一)两阶段分位数回归与最小二乘回归的比较分析
从表3和图1可以看出,第一阶段股指期货分位数回归模型中成交量的回归系数均大于零。在0.1分位点,回归系数较大,其余随着分位数的逐渐增加,回归系数呈递增趋势。这说明随着收益率的逐渐增加,成交量所起到的解释作用逐渐增强,二者呈正相关关系。成交量回归系数的变化范围从0.000438到0.004432,变动幅度为0.003994。
从表2和表3股指期货第一阶段分位数回归与最小二乘回归估计的结果比较来看,分位数回归系数存在明显差异,各不相同,而普通最小二乘回归系数与中位数回归系数很接近。在低分位数,最小二乘回归系数高于分位数回归系数,高估了成交量的作用;在高分位数,最小二乘回归系数低于分位数回归系数,低估了成交量的作用。
从表3和图2可以看出,第二阶段股指期货分位数回归模型中,随着分位数的增加,成交量的回归系数均大于零,且逐渐增加。这说明随着收益率的逐渐增加,成交量所起到的解释作用逐渐增强,二者呈正相关关系。成交量回归系数变化范围从0.00232到0.01066,变动幅度为0.00834。
从表2和表3股指期货第二阶段分位数回归与最小二乘回归估计的结果比较来看,分位点不同,分位数回归系数不同,而普通最小二乘回归系数与中位数的回归系数很接近。在低分位数,最小二乘回归系数大于分位数回归系数,高估了成交量的作用;在高分位数,最小二乘回归系数小于分位数回归系数,低估了成交量的作用。
(二)第一阶段与第二阶段分位数回归结果比较分析
1.常数项在两个阶段不同。第一阶段即调整阶段常数项回归系数均小于零,而第二阶段上升阶段0.5分位数(包括0.5分位数)以左常数项回归系数小于零,0.5分位数以右常数项回归系数大于零。第一阶段常数项回归系数波幅为0.024332,第二阶段常数项回归系数波幅为0.035665。说明第一阶段股指期货收益率随成交量的变化相对较平稳,第二阶段二者变化幅度较大。
2.成交量回归系数在两阶段均为正数,且随着分位点的增加,回归系数逐渐增加。这说明总体上股指期货市场收益率与成交量呈正相关关系,即成交量随着股指期货收益率的增加而上涨,成交量的下跌又会引起股指期货收益率萎缩,二者呈现“价量齐扬”“量缩利减”的现象。两阶段成交量回归系数波幅不同,第一阶段波幅为0.003994,第二阶段波幅为0.00834。第一阶段回归系数整体变动曲线较平稳,第二阶段在低分位点和高分位点变动幅度较大,说明第二阶段股指期货收益率对于成交量的敏感大于第一阶段。这反映出我国股指期货市场符合广义混合分布假说理论,并具有较强的投机性。
3.两阶段在涨跌停板附近,0.01分位数成交量回归系数小于0.99分位数斜率估计值,说明在跌停板附近价跌量涨效应弱于在涨停板附近价量齐扬效应,即巨量涨停和无量跌停的现象更容易出现。
(三)分位数回归检验
1.斜率相等检验(Quantile Slope Equality Test)
分位数回归估计的一个重要的检验是斜率相等检验,即检验对于不同的分位点,估计得到的结构参数(在线性模型中即为斜率)是否相等,即检验第与第分位数回归斜率是否相等。原假设设定为:
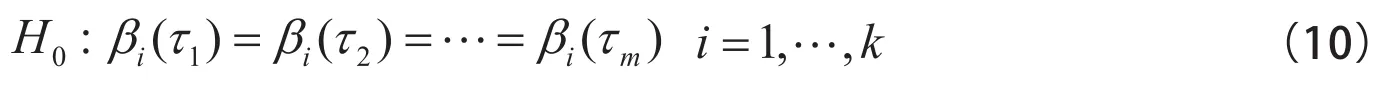
第一阶段斜率相等检验的wald统计量为12.18946,自由度为8,概率P值为0.0100。第二阶段斜率相等的wald统计量为8.920712,自由度为8,概率P值为0.0230。两阶段在95%置信水平下均拒绝原假设,说明0.10,0.20,…,0.90分位数回归的斜率不相等,股指期货收益率与成交量总体呈动态正相关关系,成交量在价格上涨和下跌时的变化是不稳定的,同时具有明显的不对称性。
2.对称检验(Symmetric Quantiles Test)
分位数回归的对称检验是检验对称的分位数回归估计出的系数的平均值是否与中位数回归的系数估计值相等。
检验结果显示,第一阶段wald统计量13.78483,自由度为8,概率p值0.0875,第二阶段wald统计量为14.9999,自由度为8,概率密度为0.0591,因此两阶段均不能拒绝原假设,即各分位点分位数回归系数估计值关于中位数对称。
五、结论及政策建议
(一)结论
本文尝试以分位数回归来分析我国股指期货市场价量关系,根据股指期货市场价格走势情况,将其分为下降调整阶段和快速上升下降两个阶段进行分析,研究结论如下:
1.对比分位数回归和最小二乘回归发现,分位数回归方法可以很好的克服最小二乘回归的描述总体平均信息以及易受极端值影响等不足,充分揭示条件分布函数在各个点的局部信息,清晰地发现低价量区(第一阶段)和高价量区(第二阶段)内股指期货成交量对收益率的影响,从而细化股指期货价格波动与成交量的关系。
2.从价量关系总体分析,两阶段具有共性:股指期货收益率的上升伴随着成交量的上涨,出现“价量齐扬”的现象;股指期货收益率下降伴随着成交量的下跌,出现“量缩利减”的现象;在涨跌停板附近,价跌量涨效应弱于在涨停板附近价量齐扬效应。这说明我国股指期货市场符合混合分布假说理论,即成交量和绝对价格变动由到达市场的信息流共同驱动。
3.在两阶段的对比分析中发现,第二阶段成交量回归系数波动幅度大于第一阶段,说明第二阶段收益率受成交量的影响大于第一阶段,第二阶段风险大于第一阶段。
4.在分位数回归斜率相等检验以及斜率对称检验中发现各分位点的分位数回归斜率不相等,且具有明显的不对称性,说明我国股指期货市场投机性较强。
(二)相关政策建议
1.规范信息披露机制。信息投资者借助信息先知性人为再造信息,导致非信息投资者对信息估计产生误差,出现投机和操纵市场的行为。为了股指期货市场的健康有序发展,改善信息披露不对称不均衡等问题,应加强我国信息披露系统的建立。有关部门在发布和披露信息时,应注意信息流对股指期货市场波动产生的影响。
2.完善我国股指期货市场法律法规。我国股指期货市场发展初期过度投机现象较为明显,投资者利用其高杠杆效应进行投机,因此严格的监管体系对股指期货市场的稳定具有重要的意义。目前,我国金融期货交易所已颁布《中国期货交易所交易规则》《中国金融期货交易所结算细则》《中国金融期货交易所会员管理办法》等法律法规,但是还不够完善,应针对股指期货市场监管、交易、结算以及风险控制制定具体法律法规,形成证监会依法监管和交易所自律管理的股指期货监管体系。
3.加强投资者市场的培育工作。股指期货专业性较强、风险程度较高,其投资理念与现货市场有本质的区别,而且在交易标的、风险特征和运行规律等方面与商品期货也有着很大的不同。这就需要相关组织积极进行期货投资知识的宣传和教育,增强投资者对股指期货投资的风险意识以及决策水平,促进其更科学理性地参与市场。
[1] Clark P.A Subordinated Stochastic Processmodels with Finite Variance for Speculative Prices [J].Econometrica.1973,(41).
[2] T.Epps,M.Epps.The Stochastic Dependence of Security Price Changes and Transaction Volume Implications for theMixture of Distribution Hypothesis [J].Econometrica.1976,(44):305-321.
[3] Board J.L.G,C.M.S.Sutcliffe.Information,Volatility,Volume and Maturity:an Investigation of Stock Index Futures [J]. Review of Futures Markets.1990,19 (3):533-549.
[4] Tauchen,G.E.,Pitts.M.The Price Variability-Volume Relationship on Speculative Markets[J]. Econometrica,1983,51:485-505.
[5] Comell B. The Relation Between Volume and Price Variability in Futures Markets[J].Joumal of Futures Markets,1981,1:303-316.
[6] Copeland T.A Model of Asset Trading Under the Assumption of Sequential Information Arrival [J].Journal of Finance. 1976,31:1149-1168.
[7] McCarthy,J. Najand,M.State Space Modeling of Price and Volume Dependence:Evidence from Currency Futures[J]. The JoumaI of Futures Markets,1993,13:335-344
[8] Kocagil,A.E.and Shachmurove,Y.Return-Volume Dynamics in Futures Markets[J].The Journal of Futures Markets,1998,18:399-426.
[9] 陈星.期货市场量价关系:基于分位数回归模型的实证分析[J].南方经济,2009,(7):50-60.
[10] 陈晓杰,黄志刚.台湾股指期货的价量动态关系-实证分析及对大陆的启示[J].台湾农业探索,2007(6):11-15.
[11] 李丹.蔡义杰.期货市场交易量与收益及波动关系的分位分析[J].经济问题, 2009(2):111-113.
[12] Koenke.R,Bassett.G.Regression Quantiles[J].Econometrica,1978,46:33-50.
(责任编辑 王 珑)
The Relationship of the Price Volatility of the China's Stock Index Futures' and Volume:Based on Quantile Regression Model
YANG Shuang-hui
(College of Finance,Fujian Jiangxia university,Fuzhou,350108,China)
Based on the theory of mixture distribution hypothesis,a quantile regression method is used to analyze the relationship between stock index futures price and trading volume in Shanghai and Shenzhen stock index 300.The results show that:On the whole,there is a positive correlation between stock index futures market yields and volume.Near the limit down price down volume up is weaker than near the limit up price and volume simultaneous rise.The regression coefficient of the second phase fluctuations is larger,which means that the second phase of the market risk is greater than the first stage.Stock index futures market returns and trading volume on the whole show a dynamic positive correlation.In the price rise and fall,volume is instability and asymmetry.This reflects our country stock index futures market speculation is strong.It needs to take measures to improve the operation efficiency and give full play to the function of the futures market.
stock index futures;volume;quantile regression
F832.51;F224
A
2095-2082(2016)02-0012-08
2015-10-16
杨双会(1981—),女,河北保定人,福建江夏学院讲师,福州大学经济与管理学院博士研究生。
