声场中椭球形气泡的体积振动研究

马　艳， 林书玉， 徐　洁， 唐一璠

(1 陕西师范大学 物理学与信息技术学院， 陕西 西安 710119;2 宁夏师范学院 物理与电子信息工程学院， 纳米结构及功能材料工程技术研究中心， 宁夏 固原 756000)



声场中椭球形气泡的体积振动研究

马艳1，2， 林书玉1*， 徐洁1， 唐一璠1

(1 陕西师范大学 物理学与信息技术学院， 陕西 西安 710119;2 宁夏师范学院 物理与电子信息工程学院， 纳米结构及功能材料工程技术研究中心， 宁夏 固原 756000)

利用Lagrange方程得到了3个半轴呈一定比例的椭球形气泡的体积振动方程，探讨了不同驱动声场、不同半轴比例下椭球形气泡的体积振动和共振频率，并与同样体积下的球形气泡进行对比。结果表明：同样声场驱动下，椭球形气泡的体积变化振幅小于球形气泡体积变化振幅，椭球形气泡越偏离球形，气泡体积改变量越小，反之亦然；椭球形气泡的共振频率取决于其3个半轴长度的比值和气泡均衡体积。

Lagrange方程； 椭球形气泡； 体积振动； 共振频率

PACS: 43.20.+g，43.35.+d，47.55.dd

超声空化是超声在含气泡液体传播过程中出现的特殊物理现象，单个球形气泡在周期性声场驱动下的动力学已经被广泛研究。1917年Rayleigh[1]忽略了液体的表面张力、气泡内的水蒸气、液体的粘滞性和可压缩性等对气泡振动的影响，第一次推导了单个球形气泡的径向运动，即Rayleigh方程，为空泡动力学奠定了基础。随后，单个气泡的声致发光现象(sonoluminescence，SL)又一次激发了人们对振荡声场中悬浮气泡动力学的兴趣[2-4]，光学测量实验表明：气泡在声场中形状并非全是球形，气泡的形状取决于气泡的均衡半径和驱动声压振幅[5]，小的气泡由于表面张力的作用，会趋于球形，较大的气泡会偏离球形。20世纪50年代起，人们对非球形气泡展开了研究[6-8]，通常的做法是在球形气泡的基础上基于微扰理论进行修正[9-10]，这样做的缺点是修正系数复杂，整个非球形气泡的动力学建立在球形气泡的基础之上。而Lagrange方程与气泡形状无关，理论上可以求得椭球形气泡的体积振动方程，本文试图从Lagrange方程出发，建立3个半轴符合一定比例的椭球形气泡的体积振动方程，并对椭球形气泡在声场中的振动进行研究，对声场中大气泡的振动理论作以修正。

1 椭球形气泡体积振动方程

球形气泡处在声场中，在声场的作用下做周期性的收缩扩张振动，如果气泡周围的液体不可压缩，气泡在振动中为绝热过程，且不考虑表面张力的作用，则球形气泡的体积振动方程[11]可表述为

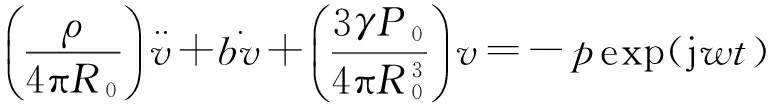
(1)

其中：ρ为液体密度，v为球形气泡体积改变量，点代表对时间求一阶导数，R0为球形气泡均衡半径，p为驱动声场声压幅值，w为驱动声场的角频率，γ为气泡内气体的等压热容量与等容热容量之比，b为耗散系数，(1)式经变形后就是R-P类型方程。

对于椭球形气泡，利用Lagrange方程也可以求得其振动方程，在只含有一个气泡的液体系统中，其系统的拉格朗日方程可表示为

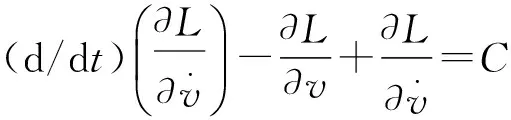
(2)

其中：L为Lagrange函数，C为驱动声场。为了求得椭球气泡系统的Lagrange函数，设椭球形气泡在x、y、z三个半轴上的长度分别为a、b、c，a为椭球气泡最短轴长度，且b=c=ka，k为常数。假设椭球形气泡为绝热振动且气泡内的气体为理想气体，忽略表面张力，根据理想气体绝热方程，可得系统的势能为

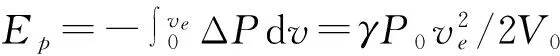
(3)

(3)式ve中为椭球形气泡的体积改变量，V0为椭球形气泡的均衡体积。由于气泡振动，引起液体动能的增量为

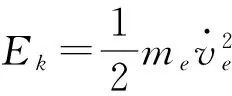
(4)

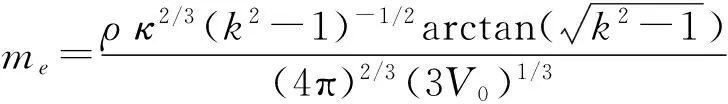
(5)

(5)式中V0为椭球形气泡的均衡体积。联立(3)、(4)和(5)式可得椭球形气泡系统的Lagrange函数为

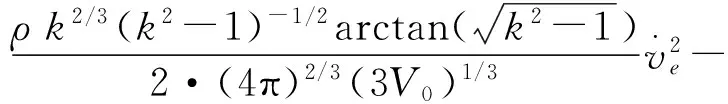
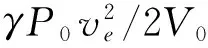
(6)

将(6)式代入(2)式，可得半轴长度呈比例的椭球形气泡的体积振动方程为

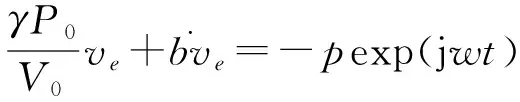
(7)

(7)式为椭球形气泡的体积振动方程，其振动状态与椭球形气泡的均衡体积和半轴长度比例系数有关。当椭球形气泡的形状无限趋于球形气泡时，上述椭球形气泡的体积振动方程就回归到球形气泡的体积振动方程(1)。

2 椭球形气泡的体积振动

小的气泡由于表面张力的作用，其形状趋于球形，故我们在研究中，模拟的气泡尺寸都在几十微米以上。图1是同样均衡体积下，不同半轴比例下的椭球形气泡和球形气泡二维对比图，对于这样尺寸的大气泡来说，在声场的作用下将会做小振幅运动，向液体介质辐射声波。在同样的声场驱动条件下，我们将对均衡体积相同的球形气泡和椭球形气泡的振动做一对比研究，得到液体中大尺寸且轻微偏离球形的气泡体积的振动规律。

图2是椭球形气泡3个半轴长度a、b、c在不同比例下体积改变量与同样均衡体积下球形气泡体积改变量的对比图，图中的模拟条件为：驱动声场压强振幅p=1.5×105Pa，ρ=1 000 kg/m3，δ=0.1，σ=0.072 5 N/m，γ=1.4，P0=1.05×105Pa，R0=50 μm。从图中可以看到：同样的均衡体积下，椭球形气泡的体积变化曲线明显不同于球形气泡的体积变化曲线，椭球形气泡的体积变化振幅小于球形气泡的体积变化振幅。具体原因为：球形气泡是一个完全对称的振动体，其等效振动质量大于相同均衡体积下的椭球体等效振动质量。除此而外，对于椭球体而言，其在声场中的振动不完全对称，与r和θ均有关系，其能量耗散要大于均衡体积下的球形气泡，其等效振动质量小于均衡体积下的球形气泡。综上所述，由于形状的不对称性，会使得气泡的等效振动质量减小，从而使得气泡在整个振动过程中体积改变量减小。

图1　相同均衡体积下不同的椭球形气泡和球形气泡的二维对比图

对比图2可以看出，虽然椭球形气泡的体积变化振幅小于均衡体积下球形气泡的体积变化振幅，但是半轴长度的比例仍然会影响椭球形气泡的体积振动。图2a中椭球形气泡三个半轴长度的比值为1∶1.2∶1.2，如图2a中实线所示，其体积改变量随时间变化的曲线与相同均衡体积下球形气泡体积改变量与时间的关系曲线(图2a中虚线)基本重合，上述模拟条件下椭球体体积振动曲线和同样体积下球形气泡一样出现了明显的周期性变化，开始做小幅周期振动。而当椭球形气泡半轴长度比值为1∶2∶2(图2b)，1∶3∶3(图2c)和1∶4∶4(图2d)时，可以看出，随着半轴比例常数的增大，椭球形气泡的体积变化曲线在振幅和相位上都与相同均衡体积下的球形气泡有一定差异。

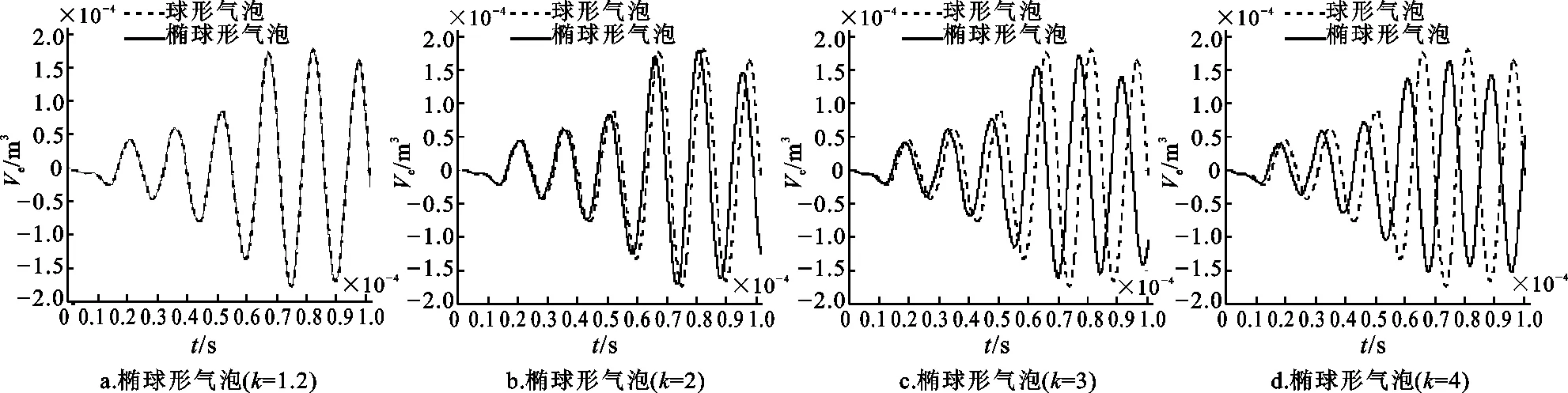
图2　相同均衡体积下不同椭球形气泡和球形气泡体积改变量对比图

以球形气泡和同样体积下的椭球形气泡第4次体积改变量为例，球形气泡第4次由体积最小扩张至体积最大时，其体积改变量为1.748×10-11m3，而同样均衡体积下k=1.2、k=2、k=3、k=4的椭球形气泡第4次由体积最小扩张至体积最大时，其体积改变量分别为1.734×10-11m3、1.688×10-11m3、 1.547×10-11m3和1.357×10-11m3。对比2a—d图可以看出：椭球形气泡的初始形状越偏离球形气泡，其做小振幅运动的体积改变量与同样体积下球形气泡的体积改变量差值越大，而椭球形气泡的初始形状越接近球形，其体积改变量与同样均衡体积相同球形气泡的差值越小，运动规律越接近球形气泡。

图3是声场驱动频率为20 kHz，三个半轴长度的比值为1∶4∶4，不同均衡体积的椭球形气泡的体积变化与时间关系图，图中虚线、圆点实线、实线所对应的椭球形气泡的均衡体积分别等价于50 μm、80 μm和100 μm球形气泡的均衡体积。对比可以看出：当声场驱动频率和椭球形气泡的初始形状一定时，椭球形气泡做小振幅振动的体积改变量取决于气泡的均衡体积，在一定条件下，气泡的均衡体积越大，其体积改变量越小，均衡体积越小，其体积改变量越大。

图4a和4b是a=20 μm，k=4的椭球形气泡，当改变驱动声场的声压振幅和驱动频率时，其体积随时间的变化关系。通过对比可以看出，一定初始体积的椭球形气泡，当固定声场驱动频率为20 kHz，改变其声场的驱动声压从1.5×105Pa到2.0×105Pa，再增大到2.5×105Pa，从数值模拟结果看来：当驱动声压大于1.5×105Pa时，再增大驱动声压振幅对椭球形气泡的体积改变量影响不大；当驱动声压振幅固定为1.5，改变声场驱动频率从20 kHz 增大到50 kHz，再增大到100 kHz，结果发现：驱动频率的改变对椭球形气泡的体积改变量影响较大，可通过选择不同的驱动频率来控制椭球形气泡的体积振动幅度。

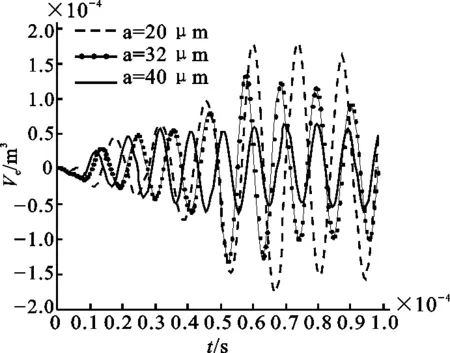
图3　不同初始体积下的椭球形气泡

3 椭球形气泡的共振频率

当球形气泡在声场驱动下做周期性扩张和收缩时，可以从球形气泡的体积振动方程(1)中解得球形气泡的共振频率为

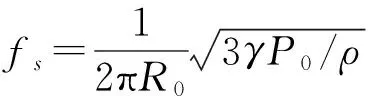
(8)

(8)式也是著名的Minnaert 共振频率方程，对于椭球形气泡可以使用同样的方法从椭球形气泡体积振动方程中求解其共振频率，从(7)式中可解得椭球形气泡的共振频率为

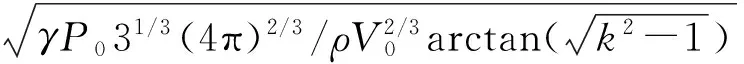
(9)

图5是均衡体积相同，不同半轴长度比例下椭球气泡共振频率和球形气泡共振频率的对比图。如果均衡体积相同，球形气泡的共振频率(图5中标记符号为×的曲线所示)小于椭球形气泡的共振频率，这是由于气泡在声场作用下做周期性扩张收缩运动时，气泡的形状对气泡的等效振动有一定的影响，同样条件下球形气泡的等效振动质量大，而椭球形气泡的等效振动质量小。如果忽略表面张力的作用，均衡体积相同的球形气泡和椭球形气泡系统的劲度系数是相同的，所以，同样条件下球形气泡的共振频率小于椭球形气泡的共振频率。

同样均衡体积下，椭球形气泡的共振频率也不相同，而是取决于椭球形气泡3个半轴长度的比例(如图5中不同形状的数据点)，3个半轴a∶b∶c=1∶4∶4的椭球形气泡的共振频率，如图中实线所示，在同样的均衡体积下，其共振频率最大。3个半轴a∶b∶c=1∶3∶3的椭球形气泡的共振频率，如图中标记符号为圆点曲线所示，在同样的均衡体积下，其共振频率次之。3个半轴a∶b∶c=1∶2∶2的椭球形气泡的共振频率最小，如图中标记符号为三角的曲线所示，最接近同样体积下的球形气泡的共振频率(如图5标记符号为×的曲线)。图中方块数据点是文献[12]的测量结果，对比发现本文模拟结果与测量结果符合较好，这证明了椭球形气泡体积振动方程和频率方程推导的正确性。

图5　椭球形(球形)气泡共振频率随

通过以上数值模拟可以看出：同样均衡体积的椭球形气泡，其共振频率取决于其3个半轴长度的比值和气泡均衡体积，一定均衡体积的椭球形气泡，其形状偏离球形越大，则共振频率越大，反之亦然。

4 结论

非球形气泡的形状稳定性研究一直是气泡空化动力学的热点问题，然而由于非球形气泡形状和计算的复杂性，只局限在对球形气泡运动方程的修正上，无法直接得到非球形气泡的运动方程。本文基于Lagrange方程，直接得到了3个半轴长度呈一定比例的椭球形气泡的体积振动方程，并研究了尺寸在几十微米级别的椭球形气泡的体积振动规律和共振频率，研究发现当液体中存在大量大尺寸的非球形气泡时，其声场效应不同于同样体积下的球形气泡的声场效应。由于计算的复杂性，本文只考虑了3个半轴呈一定比例的椭球形气泡的振动规律，3个半轴长度无规律的椭球形气泡的振动将是我们下一步研究的重点内容。

[1] RAYLEIGH L. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. Philosophical Magazine, 1917, 200(34): 94-98.

[2] GAITAN D F, CRUM L A, ROY R A. Sonoluminescence and bubble dynamics for a single, stable, cavitation bubble[J]. The Journal of Acoustical Society of America, 1992, 91(6): 3166-3183.

[3] 谢崇国，安宇. 声致发光气泡内水蒸气的影响[J]. 物理学报，2003, 52(1): 102-107.

[4] CRUM L A. Sonoluminescence, sonochemistry, and sonophysics[J]. The Journal of Acoustical Society of America, 1994, 95(1): 559-562.

[5] REDDY A J, SZERI A J. Shape stability of unsteadily translating bubbles[J]. Physics of Fluids, 2002, 14(7): 2216-2224.

[6] MOSS W C, LEVATIN J L. A new damping mechanism in strongly collapsing bubbles[J]. Proceedings of the Royal Society of London Series A, 2000, 456: 2983-2994.

[7] WANG W J, CHEN W Z. Bubble oscillations driven by aspherical ultrasound in liquid[J]. The Journal of Acoustical Society of America, 2003, 144(4): 1898-1903.

[8] BOGOYAVLENSKIY V A. Single-bubble sonoluminescence: shape stability analysis of collapse dynamics in a semianalytical approach[J]. Physical Review E, 2000, 42(6): 2158-2167.

[9] CHEN W Z. Single bubble sonoluminescence driven by non-simple-harmonic ultrasounds[J]. The Journal of Acoustical Society of America, 2002, 111(6): 2632-2637.

[10] PELEKASIS N A, TSAMOPOUSLOS J A. Equilibrium shapes and stability of charged and conducting drops[J]. Physics of Fluids A, 1990, 2(8): 1328-1344.

[11] DEVIN C. Survey of thermal, radiation, and viscous damping of pulsating air bubbles in water[J]. The Journal of Acoustical Society of America, 1959, 31(12): 1654-1667.

[12] STRASBERG M. The pulsation frequency of nonspherical gas bubbles in liquids[J]. The Journal of Acoustical Society of America, 1953, 25(3): 536-537.

〔责任编辑 李博〕

Volume pulsation of an ellipsoidal gas bubble in an acoustic field

MA Yan1,2, LIN Shuyu1*, XU Jie1, TANG Yifan1

(1 School of Physics and Information Technology, Shaanxi Normal University,Xi′an 710119, Shaanxi, China；2 School of Physics and Electronic Information Engineering, Engineering Research Center of Nanostructure and Functional Materials, Ningxia Normal University, Guyuan 756000, Ningxia, China)

The volume pulsation equation of three ellipsoidal gas bubbles are obtained based on Lagrange′s equation. The volume pulsation and resonance frequency of an ellipsoidal gas bubble are researched.The volume pulsation of an ellipsoidal gas bubble and a spherical gas bubble with the same equilibrium volume are compared. The results show that the volume change of an ellipsoidal gas bubble is smaller than the spherical gas bubble with the same equilibrium volume.Comparing with sphere, the change of volume in the ellipsoidal gas bubble is smaller. The shape of ellipsoidal gas bubble is close to sphere, and the change of volume is bigger. The resonance frequency of an ellipsoidal gas bubble depends on the equilibrium volume and the ratio of semiaxis of the ellipsoidal gas bubble. Keywords: Lagrange′s equation; ellipsoidal gas bubble; volume pulsation; resonance frequency

1672-4291(2016)04-0028-05

10.15983/j.cnki.jsnu.2016.04.242

2016-03-01

国家自然科学基金(11174192，11374200，11474192); 宁夏师范学院校级项目(NXSFZD1516)

林书玉，男，教授，博士生导师。E-mail: sylin@snnu.edu.cn

O426.1

A