一种改进的高效用频繁集挖掘算法
2016-08-09汪峰坤张婷婷
汪峰坤,张婷婷
安徽机电职业技术学院信息工程系,安徽芜湖,241000
一种改进的高效用频繁集挖掘算法
汪峰坤,张婷婷
安徽机电职业技术学院信息工程系,安徽芜湖,241000
摘要:运用(k-1)阶频繁集与1阶频繁集中较少项数的频繁集组合生成k阶频繁候选项、使用最大效用值系数、各阶频繁项集最大数目限制三种方法,对高效用频繁集数据挖掘经典算法Two-Phase进行了改进,研究了在低维数据集上不同数据量、高维数据集上不同数据量和不同维数数据集改进算法了运行时间。结果表明:改进方法的算法在高数据量和高维数据集中提高了算法运行效率,减少了运行时间。实验表明,在高维和百万数据级的数据集上,执行时间相对于Two-Phase算法至少节约了50%。
关键词:数据挖掘;关联规则;频繁项集;高效用项集
在经典的关联规则生成算法中,对事务数据库中所有的项集的重要性假定是同等的,仅仅是根据项集在事务集中出现的次数来判断项之间的关联情况。在实际的一些数据挖掘应用中,既要考虑项集出现的次数,又要考虑项集的重要性。例如,在职工体检中,不同的检测项的重要性是不一样的。
针对此类问题,B.Barber等提出了基于“效用”的挖掘概念[1]。项的“效用”值是用户设定的用于反应项的权重、收益、消费等内容的整数值。如果某项集的效用值不小于用户设定的阈值,则此项集被称为高效用频繁项集(HUI)。
基于效用的关联规则挖掘算法最基本的是枚举方法,其时空性能差,一般只用于验证其他算法的正确性。Ying Liu等提出了Two-Phase算法[2],此算法对效用值的计算公式进行了修改,使新定义的效用值满足“事务权重向下闭属性”性质。Erwin A等提出了CTU-Mine算法[3],通过一次扫描事务集,在内存中生成表示所有事务的树状结构,减少了事务集的读取次数。以上算法会生成非常多的频繁项目集和关联规则,算法的执行时间较长,也不利于决策者对求解的关联规则进行分析[4]。
本文针对Two-Phase算法进行改进,提出了用于生成精简频繁项集的近似算法CAMine算法。CAMine算法的改进主要体现在以下几方面:优化k阶频繁候选集的生成、使用最大效用值系数、使用各阶频繁项集限数等优化策略。经过实验仿真,本算法的运算效率大大提高。
1问题描述和相关定义
定义1设事务数据库DB={T1,T2,…,Tn},其中Ti(i∈[1,n])为DB中的一条事务。项目集合I={I1,I2,…,Im},其中Ii(i∈[1,m])为项集中的一个项目。|DB|为事务数据库中事务个数。|I|为项目集中项目个数。
定义2本地事务效用值(LocalTransactionUtilityValue),数值型数据,是客观数据,反映某事务中项出现的次数,记为o(ip,Tq),如表1中,o(E,T4)的值为15。

表1 事务数据库
定义3外部效用(ExternalUtility)是使用者主观赋予项的一个实数值,以反映此项的语义特征,记为s(ip),可用来表示项的重要性、成本、收益、价值等。例如,由表2可得E的外部效用:s(E)=10。

表2 外部效用表
定义4事务Tq中项ip的效用值表示某项在某条事务中给用户带来的效用值,记为:u(ip,Tq)。计算公式为:u(ip,Tq)=o(ip,Tq)*s(ip),例如:u(E,T4)=o(E,T4)*s(E)=15*10=150。



定义8高效用频繁候选集和高效用频繁项集:如果项集满足u′(Ik)≥MinUtilNum,则项集Ik是高效用频繁候选集。如果项集满足u(Ik)≥MinUtilNum,则项集Ik是高效用频繁集。
性质1高效用频繁项集的向下闭包性质:设Ik是k-项集,Ik-1为(k-1)项集,其中Ik-1⊂Ik。如果Ik是高效用频繁项集,则Ik-1也是高效用频繁项集。
本算法新增定义如下:
定义9各阶频繁项集最大数目MAXFI:整数值,指每一阶频繁项集的最大数目。
定义10项集X的最大效用值系数MUC:整数值,指任何项集X的最大效用值的限定系数,即u(X)=MAX(u(X),MUC×MinUtilNum)。
定义11最小效用阈值比例MinUtil:百分比值,表示最小效用阈值占数据集事务个数的比例,即MinUtilNum=MinUtil×|DB|。
2改进算法
2.1算法的基本数据结构
项目结点Ii包括项目名称、本地事务效用值o和项目效用值u。
项目集I={I1,I2,…,Im}的数据结构包括表示组成项目集I的所有项目的列表集合、项目效用值u、期望效用值up、本项集的支持数SupNum。
K-阶项集Ik的数据结构:用来表示所有的k-阶的频繁项和频繁候选项,主要的数据结构是双向链表,链表的每个结点是一个k阶的项目集I。
各阶频繁项集数组指针结构(Pointer):数组下标对应阶数,数组的元素是指针,指向各阶频繁项集。
2.2CAMine算法流程
当前主流的高效用频繁集计算算法有如下缺点[5-7]:(1)合适的MinUtilNum值确定困难。(2)由于高效用值u不满足反单调性,当前算法优化的主要策略是“定义更加宽松的效用期望效用值up”,利用up的向下闭包性质减少候选集数目。但是维数较多时,up值与相应的u值相差很大,生成高效用候选集时,容易造成组合爆炸情况的产生。(3)维数较多时,u值增加非常快,经常出现超过整数范围的错误。(4)在实际使用中,更期望在合理的时间内得到适量的高效用频繁集,用于决策支持。而当前的主流算法是生成所有的高效用频繁集,在数据量较大或维数较多时,算法运行时间过长。
本算法的改进方法主要有:(1)生成k阶频繁候选集时,比较(k-1)阶频繁候选集的长度与一阶频繁候选集长度,利用长度低的候选集与(k-1)阶频繁候选集组合生成阶频繁候选集。当候选集长度越长,阶数越多时,此优化方法效果越明显。(2)定义项集X的最大效用值系数MUC,当频繁集的效用值远大于最小效用阈值MinUtilNum时,为了防止计算溢出,将频繁集的效用值设为MUC×MinUtilNum。这样,既保证了计算不会溢出,又表示频繁集的效用。(3)本算法引入了各阶频繁项集最大数目MAXFI,通过对各阶频繁项集按效用值u降序排序,只保留前MAXFI项,避免了由于最小效用阈值MinUtilNum过小造成的各阶频繁项集组合爆炸问题。
CAMine算法流程如下:
(1)第一遍扫描事务数据库DB,统计每一项目结点的效用值u,生成一阶频繁候选集。

(3)第二遍扫描事务数据库DB,计算二阶高效用频繁候选集每一个候选项的效用值u、期望效用值up和支持数SupNum。
(4)扫描二阶频繁高效用候选集,去除期望效用值up小于最小效用阈值MinUtilNum的候选项。
(5)对于k阶(k>2)高效用频繁候选集,设(k-1)阶高效用频繁集长度为nk-1。如果nk-1>n1,则k阶高效用频繁候选集由(k-1)阶高效用频繁集与1阶高效用频繁候选集组合生成。否则,k阶高效用频繁候选集由(k-1)阶高效用频繁集与自身组合生成。
(6)扫描事务数据库DB,计算k阶高效用频繁候选集每一个候选项的效用值u、期望效用值up和支持数SupNum。
(7)k阶高效用频繁候选集按u值排序,扫描生成的k阶高效用频繁候选集,删除up小于MinUtilNum的候选项。如果u值大于MUC×MinUtilNum,则u值取MUC×MinUtilNum,并且只保留前MAXFI项。
如果k阶高效用频繁候选集不为空,则转向步骤(5),计算下一阶,否则转向步骤8。
(8)遍历所有阶中的候选项,删除u小于MinUtilNum的项,剩余的项就是高效用频繁集。
3CAMine算法实验与分析
3.1算法流程实验
事务数据库DB如上表1所示,外部效用表如上表2。CAMine算法的参数设置为:最小效用阈值MinUtilNum为30,各阶频繁项集最大数目MAXFI为100,项集X的最大效用值系数MUC为10。
一阶高效用频繁项为:[D,(u:48)],[E,(u:600)]。
二阶高效用频繁项为:[D,(u:48)][E,(u:600)]:[A,D,(u:47)],[A,E,(u:357)],[B,E,(u:229)],[C,D,(u:30)],[C,E,(u:102)],[D,E,(u:352)],[E,F,(u:82)]。
三阶高效用频繁项为:[A,D,E,(u:248)],[C,D,E,(u:110)],[A,E,F,(u:84)],[A,B,E,(u:78)],[B,D,E,(u:31)]。
四阶高效用频繁项为:[A,B,D,E),(u:32)]。
从挖掘的结果可以看出,外部效用值E和D在高效用频繁项集中出现的次数较多,符合外部效用值的含义。
3.2算法性能比较
本文主要比较算法CAMine和经典的Two_Phase算法的时间性能。测试数据集由修改后的IBM数据生成器生成。
(1)比较低维数据集、不同数据量的算法性能。数据生成器生成的数据集的维数是10,内部效用值为0~10,外部效用值为1~100,最小效用阈值比例MinUtil为30%。CAMine算法的MAXFI参数设置为500,MUC参数设置为100。数据量从1万条升到50万条。
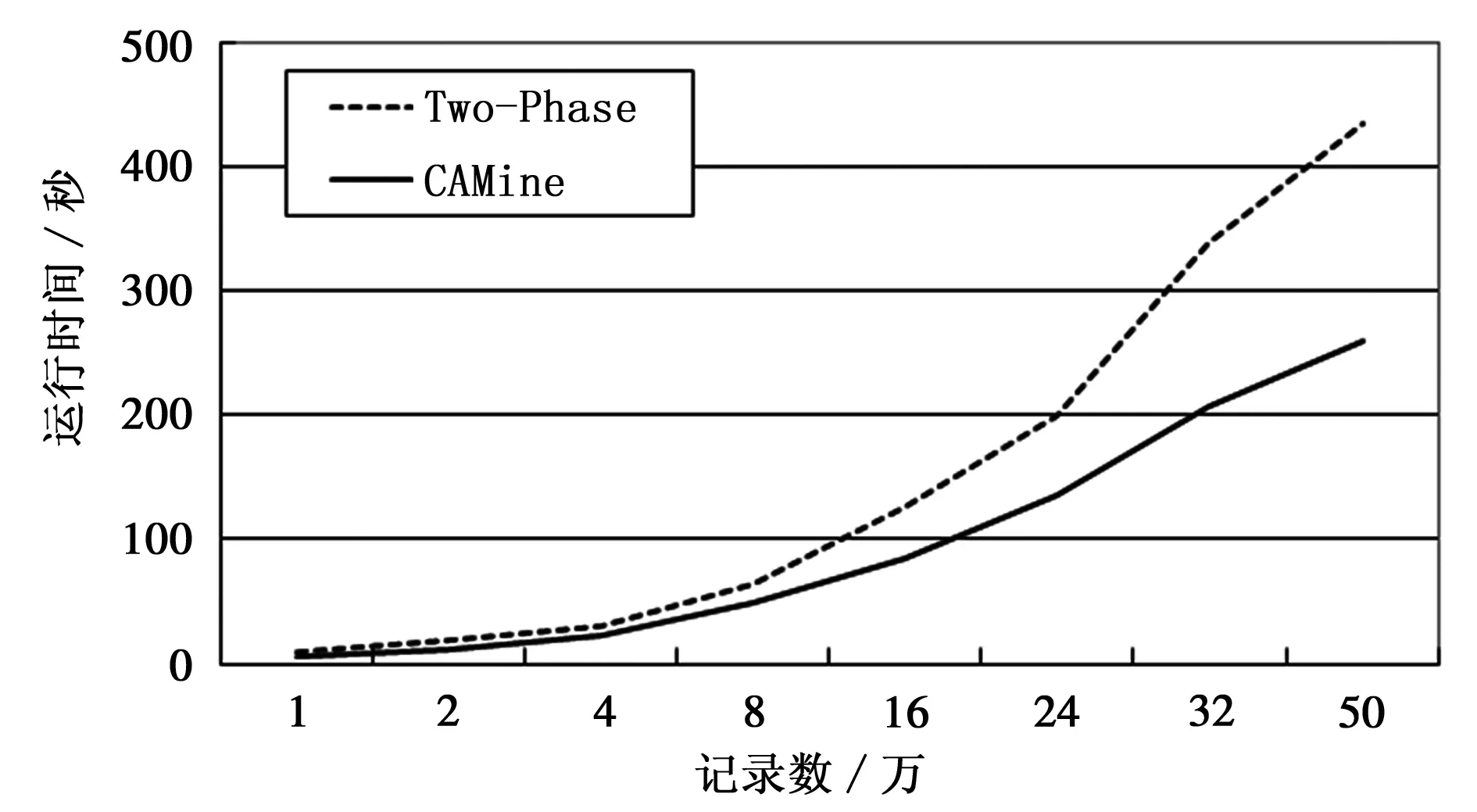
图1 低维数据运行时间和数据量关系
从图1可见,当数据维数较低时,两种算法运行速度都比较快。数据量较少时(少于16万),两种算法性能相差不多。在数据量较大时,CAMine算法要略优于Two-Phase算法,当数据量达到50万条时,改进算法所用时间减少40%。
(2)比较高维数据集、不同数据量的算法性能。数据生成器生成的数据集共有20维,内部效用值为0~10,外部效用值为1~100,最小效用阈值比例MinUtil为30%,数据量从1万条升到10万条。
从图2可见,对于高维数据集,CAMine算法明显优于Two-Phase算法,在数据量为50万条时,改进算法运行时间仅为Two-Phase算法的1/10。
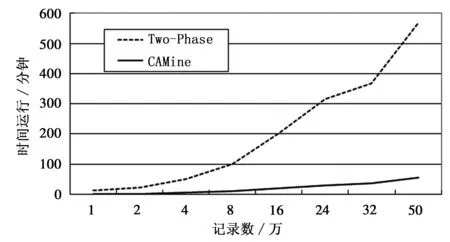
图2 高维数据运行时间和数据量关系
(3)分析给定数据量时,不同维数对算法的性能影响。数据生成器生成的数据集为5万条,内部效用值为0~10,外部效用值为1~100,最小效用阈值比例MinUtil为30%,维数从10维增加到30维。
从图3可见,Two-Phase算法对维数极其敏感,运行时间与维数接近指数关系。CAMine算法在维数较高时,算法运行时间仍然可以接受。
4结束语
Two-Phase算法求解出数据集中所有频繁集,本算法是一种近似算法,可求解出每一阶满足最小效用阈值的给定频繁项个数的

图3 不同维数据算法的性能比较
频繁集。因此,当最小效用阈值较小或维数较高时,Two-Phase算法运算时间过长,出现组合爆炸情况,而本算法可在较短的时间内完成。通过仿真,本算法性能相对于经典的Two-Phase算法有了一定的提升。
参考文献:
[1]Barber B,Hamilton H J.Extracting share frequent itemsets with infrequent subsets[J].Data Mining and Knowledge Discovery,2003,7(2):153-185
[2]Liu Y,Liao WK,Choudhary A.A Fast High Utility Itemsets Mining Algorithm[C]//New York USA:Proc of the 2005 Workshop on Utility-Based Data Mining,2005:90-99
[3]Erwin A,Gopalan R P,Achuthan N R.CTU-Mine:An Efficient High Utility Itemset Mining Algorithm Using the Pattern Growth Approach[C]//Washington DC USA:Proc.of the IEEE 7th International Conferences on Computer and Information Technology,2007:71-76
[4]祝孔涛,李兴建,王乐.高效用项集挖掘算法[J].计算机工程与设计,2013,34(12):4220-4225
[5]Agrawal R,Imielinski T,Swami A.Mining association rules between Sets of items in large databases[J].ACM SIGMOD Record,1993,22(2):207-216
[6]Agrawal R,Srikant R.Fast algorithms for mining association rules[C]//San Francisco CA USA:VLDB,94 Proceedings of the 20th International Conference on Very Large Data Bases,1994:487-499
[7]Lan G C,Hong T P,Tseng V S.Mining High Transaction-Weighted Utility Itemsets[C]//Washington DC USA:ICCEA '10 Proceedings of the 2010 Second International Conference on Computer Engineering and Applications,2010,1:314-318
[8]LAN Guo-cheng,Hong T P,Tseng V S.Efficiently mining high average-utility itemsets with an improved upper-bound strategy [J].International Journal of Information Technology & Decision Making,2012,11(5):1009-1030
(责任编辑:汪材印)
doi:10.3969/j.issn.1673-2006.2016.07.027
收稿日期:2016-02-25
基金项目:安徽省高校省级自然科学研究重点项目“基于移动客户端的教职工健康体检数据智能分析管理系统的研发”(KJ2014A038)。
作者简介:汪峰坤(1978-),安徽霍邱人,硕士,讲师,主要研究方向:数据挖掘。
中图分类号:TP301.6
文献标识码:A
文章编号:1673-2006(2016)07-0103-04
