层状土中单个管桩的竖向振动特性
2016-08-09刘林超闫启方
刘林超,闫启方,刘 滕
(信阳师范学院 土木工程学院, 河南 信阳 464000)
0 引言
在实际工程中,桩基通常要受到各种形式的外界动态激励的作用,近几十年来有关桩基振动的研究一直没有停止过,并取得了一些结果[1-5],需要指出的是,这些研究都是基于实心桩展开的.然而,随着桩基制作、设计和施工技术的发展,管桩作为一种新型桩近年来在高速铁路与公路基础、软土地基加固等众多工程领域得到了广泛应用.
管桩内土塞(桩芯土)受成桩效应的影响,将导致桩芯土的层状性质与桩周土层状性质产生较为明显的差异,这种差异使得管桩与实心桩在静、动力学特性方面必然存在差异,所以管桩振动特性的研究较实心桩复杂.基于均质土介质理论,郑长杰等[6-8]研究了黏弹性地基中现浇大直径管桩的纵向振动及扭转振动,并对饱和土地基中现浇大直径管桩水平振动进行了研究;丁选明等[9]求得了大直径管桩在瞬态集中荷载作用下振动响应时域解析解;刘林超等[10]运用多孔介质理论对饱和土中管桩的水平振动进行了研究;吴文兵等[11]基于附加质量法研究了考虑土塞效应时成层地基中管桩的纵向振动问题,然而在实际工程中,桩周土和桩芯土通常具有层状特性,将桩周土和桩芯土视为均匀介质与实际工程必然不符; 栾茂田等[12]在考虑土体分层特性的基础上,采用传递矩阵法研究了实心桩的竖向振动,黄茂松等[13]、吴志明等[14]、任青等[15]采用类似的方法对实心桩的竖向和水平振动问题进行了较为深入的研究.由于管桩的出现相对较晚,目前有关层状土中管桩振动特性的研究未见报道,本文将在考虑土体分层特性的基础上采用传递矩阵法对层状土中管桩的竖向振动进行研究.
2 桩周和桩芯土层竖向振动求解
图1所示管桩在竖向简谐荷载作用下稳态振动,假定桩周土和桩芯土对应层的分层厚度相同,将其桩芯土层和桩周土层从上到下分别编码为1、2、…、i、…、n,相应的土层厚度分别为L1、L2、…、Li、…、Ln,桩的总长度为L,桩底为基岩,假定桩底与基岩完全固定.设第i层桩周土和桩芯土的剪切模量分别为Gi1和Gi2,密度为ρi1和ρi2,由于忽略土层的径向位移和环向位移能满足工程设计的需要,为了简化起见,这里仅考虑竖向位移且不考虑其随深度的变化.

图1 管桩竖向振动计算简图

桩周土
(1)
桩芯土
(2)
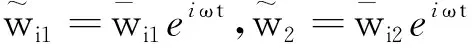
(3)
(4)
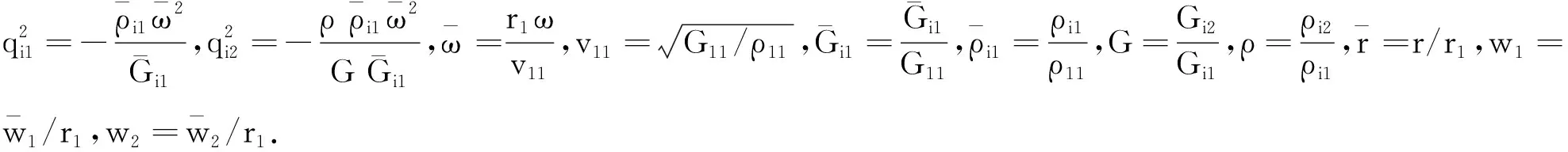
(5)

(6)
(7)
进而可以得到第i层桩周土和桩芯土的竖向剪切应力为
(8)
(9)
由式(8)和式(9)可以得到第i层桩周土和桩芯土对管桩的竖向作用力为
(10)
其中:kiz=Re(Zi),ciz=Im(Zi)分别为等效Winkler地基模型的刚度系数和阻尼系数.
3 层状土中管桩竖向振动求解
不考虑桩身的内阻尼,考虑桩周土和桩芯土对管桩的作用,可以建立无量纲化的管桩的稳态竖向振动方程为
(11)
式(11)中,li=Li/r1,

(12)
这里,Ci、Di可以根据桩端的边界条件确定.由初始参数法[17]可以建立第i段桩两端位移和轴力的关系
(13)
式(13)中,

(14)
采用传递矩阵法建立整根桩桩顶和桩底位移、轴力的关系为[12,18]
(15)
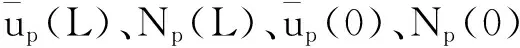
(16)
由于管桩桩底完全固结,所以桩底位移为零,由此可得
(17)
根据桩顶产生单位竖向位移,所需的竖向轴力即为管桩的竖向复刚度,由式(17)可得桩顶竖向复刚度为
(18)
4 数值算例与分析

管桩壁厚(即r2/r1)对管桩复刚度的影响见图2,可以看出,在一定范围内,r2/r1越小,即管桩管壁越厚,动态刚度因子和等效阻尼越大,由于此时接近实心桩,问题可以退化到实心桩的情形,所以管桩壁厚的影响比较小,仅在动态刚度因子和等效阻尼随无量纲频率的变化曲线的峰值处有影响;但当管桩管壁过薄时,其动态刚度因子急剧变大,且高频时动态刚度因子和等效阻尼随无量纲频率的变化曲线有较大的波动,这可能由于管壁过薄导致管桩稳定性变差的缘故.桩芯土和桩周土剪切模量对管桩复刚度的影响见图3,由于r2/r1较小时其对管桩复刚度影响不大,这里取r2/r1=0.8,可以看出桩芯土剪切模量越小,也就桩周土的剪切模量越大时,其动态刚度因子越大,这可能是因为桩周土剪切模量变大时桩周土对管桩的约束作用增大,而对等效阻尼的影响较为复杂,桩芯土剪切模量过大时等效阻尼可能为负值.图2和图3在频率较高时出现了奇点振荡,且管壁越薄振荡越明显,这可能是因为高频时管桩的稳定性较差的缘故.
当土层厚度相等时(图4),动态刚度因子和等效阻尼随频率变化曲线较为稳定,随着下层土的变厚,动态刚度因子和动态阻尼将会变大且较为复杂,这是因为计算时剪切模量随着深度的增加是逐渐增大的,相应土层厚度的增加必然会导致土层对管桩作用力的增大,可见在进行桩基设计时土层厚度和土层的剪切模量必须综合考虑.当各土层厚度相等时,各层剪切模量对管桩复刚度的影响主要在动态刚度因子和等效阻尼随频率变化曲线的峰值处(图5),在低频时中间土层剪切模量最小时动态刚度因子和等效阻尼最大,而在高频时土层剪切模量随深度逐渐减小的情况最大.桩土模量比(Ep/G11)对管桩复刚度的影响最大(图6),桩土模量比越大,管桩的动态刚度因子和等效阻尼越大,且峰值对应的频率也越大.

图2 管桩壁厚桩顶复刚度的影响
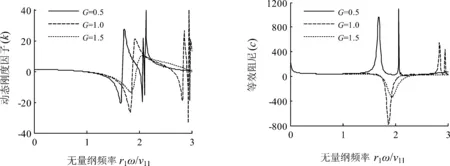
图3 桩芯土和桩周土剪切模量比对桩顶复刚度的影响

图4 土层厚度对桩顶复刚度的影响

图5 土层剪切模量对桩顶复刚度的影响

图6 桩土剪切模量比对桩顶复刚度的影响
5 结论
管桩振动特性的研究对于管桩的抗震设计和动力检测具有十分重要的工程应用价值,本文不但考虑了桩芯土对管桩振动的影响,同时又考虑了土体的分层特性,将管桩-土动力相互作用利用Winkler地基模型来模拟,求解了层状土中管桩的竖向振动.在考虑土体分层特性和桩芯土共同影响下,管桩的动态刚度因子和等效阻尼随频率变化曲线与实心桩存在一定差异;对于管桩不宜太薄,否则容易造成桩基稳定性不足;在进行管桩的设计时,既要考虑土层厚度和土层力学特性的差异,又要考虑桩周土和桩芯土力学特性的差异.由于考虑了桩芯土的影响,在桩芯土的计算中引入了第二类贝塞尔函数,可能会导致高频时数值计算结果稳定性较差.
