一个有效的无证书门限签密方案
2016-08-09崔金玲
崔金玲, 孙 华
(安阳师范学院 计算机与信息工程学院, 河南 安阳 455000)
0 引言
无证书密码的概念由AL-RIYAMI等[1]于2003提出,由于其不需使用证书,同时又克服了基于身份密码体制中的密钥托管问题,因而对无证书密码的研究引起了不少学者的兴趣,并取得了一系列的研究成果.
签密能够同时实现机密性和认证性这两个安全目标.无证书签密概念由BARBOSA等[2]于2008年提出,并且在随机预言模型下提出了一个无证书的签密方案.ARANHA等[3]提出一个仅需两个双线性对运算的无证书签密方案,然而其没有对方案的安全性进行证明.同年,WU等[4]也提出一个新的无证书签密方案,该方案在签密和解签密阶段需要4个双线性对运算,不幸的是,文献[5]指出该方案是不安全的.首个无证书多接收者签密方案由SELVI等[6]提出,然而该方案在第一类攻击者面前是不安全的.在标准模型方面,第一个无须借助随机预言机可证安全的无证书签密方案由LIU等[7]提出,然而WENG等[8]通过分析指出方案的语义安全性和不可伪造性这两个安全目标在第二类攻击者攻击下无法实现.文献[9]和文献[10]同样给出了两个标准模型下的无证书签密方案,然而它们同样是不安全的.
在面向群体的通信中,需要同时具有保密性和认证性的应用场合越来越多,而面向群体的签密体制可以较好地满足这种安全需求.门限签密不仅能够实现这一安全目标,并且能够有效防止单点失效.目前,已有的门限签密方案[11-13]大都是在身份密码体制下基于随机预言模型提出的.在该模型中,Hash函数被看成是完全随机的函数.然而在该模型下被证明是安全的方案并不代表是真正的安全,因此本文在标准模型下提出的无证书门限签密方案更有实际意义.
1 预备知识
1.1 双线性对
设G、GT是两个阶为素数p的循环群,g是群G的生成元,双线性对是具有如下性质的映射e:G×G→GT:
1. 双线性:对于任意的P,Q∈G和a,b∈Zp,都有e(aP,bQ)=e(P,Q)ab;
2. 非退化性:e(g,g)≠1;
3. 可计算性:对于任意的P,Q∈G,存在一个有效的算法计算e(P,Q).
1.2 困难问题
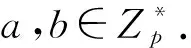
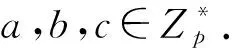
3.q-ABDHE问题:给定群G中一个含有(q+3)个元素组成的向量(g′,g′aq+2,g,ga,ga2,…,gaq)及Z∈GT,判定等式Z=e(gaq+1,g′)是否成立.
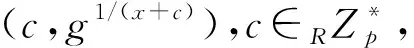
2 本文的无证书门限签密方案
方案描述:设{ID1,…,IDn}是用于产生门限签密的身份为US的n个成员集合,不妨设ID1,…,IDt是代表US对消息M进行签密的t个成员,IDR为签密接收者.给定阶为素数p的循环群G和GT,双线性映射e:G×G→GT,对于任意长度的消息M,哈希函数H:{0,1}*→{0,1}nm输出长度为nm的位串.
1)系统参数产生算法
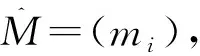
2)部分私钥产生算法
对于身份为ID∈Zp的用户,KGC任意选取rID∈Zp,计算d1=(h1g-rID)1/α-ID.如果ID=α,那么KGC将重新选择并计算;否则,令d2=rID,并将DID=(d1,d2)作为用户的部分私钥.
3)秘密值分享算法
①对于产生门限签密的各成员IDi,其首先随机选取秘密值xIDi∈Zp及系数在Zp、次数为t-1的多项式hi(x)=ci,0+ci,1x+…+ci,t-1xt-1,其中ci,0=xIDi.然后IDi向其他成员IDj(j≠i)广播参数Ei,d=gci,d(d=0,1,…,t-1),计算秘密分享xi,j=hi(j),并将它们发送给其他各成员.
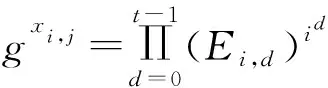
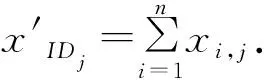
4)用户公钥产生算法
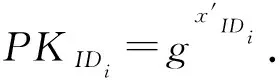
5)用户私钥产生算法
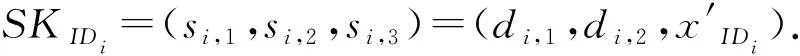
6)签密
给定用来产生门限签密的n个成员的集合US,身份为IDR的门限签密接收者,待签密消息M∈GT.各成员IDi首先产生其部分签密,然后将其发送给US中任一用以生成门限签密的集成者dealer,该过程执行如下:

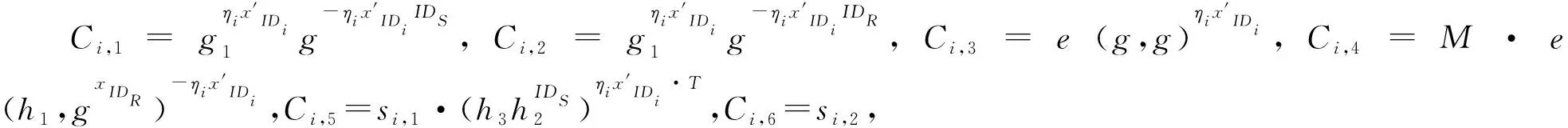
为拉格朗日系数.
③该dealer计算
则最终的无证书门限签密为C=(C1,C2,C3,C4,C5,C6,T).
7)解签密
设签密产生者的身份为IDS,签密接收者IDR的私钥为SKIDR,其在收到无证书门限签密C=(C1,C2,C3,C4,C5,C6,T)后,进行如下计算:
②如果上式成立,则C是一个有效的密文,那么签密接收者IDR能够利用其私钥SKIDR通过下式恢复出消息
3 安全性分析
3.1 方案正确性
方案的正确性很容易得到验证,限于篇幅原因这里省略.
3.2 不可区分性
定理1 如若q-ABDHE是困难问题,对于第一类攻击者AI,本方案满足适应性选择密文攻击下的不可区分性.
证明设敌手AI能够成功攻破本方案,则可以构造算法B,其可利用敌手AI解决q-ABDHE问题,而这与q-ABDHE是一个困难问题相矛盾.
输入算法B的q-ABDHE问题实例(g′,g′aq+2,g,ga,ga2,…,gaq,Z),其目标是判定等式
Z=e(g,g′)aq+1
是否满足.这里算法B模拟AI的挑战者C与其交互如下:

Phase1:敌手AI可发起如下7种形式的询问,同时算法B需使用4个初始为空的列表L1、L2、L3和L4.
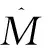
然后在列表L1中添加(M,T).
②部分私钥询问:当对身份IDi的部分私钥DIDi进行询问时,如果IDi=a,算法B可以利用a解决q-ABDHE问题;否则,令q-1阶多项式为fq-1(x)=fq(x)-f(IDi)/x-IDi,算法B计算d1=gfq-1(a),d2=fq(a),并把(IDi,DIDi)添加到列表L2中,这里DIDi=(d1,d2),最后将DIDi作为结果返回.

④用户私钥询问:当询问身份IDi的私钥SKIDi时,如果(IDi,SKIDi)存在于列表L4,则返回SKIDi;否则,算法B分别从列表L2、L3中查询(IDi,DIDi)和(IDi,PKIDi,xIDi,c),令SKIDi=(DIDi,xIDi),然后把(IDi,SKIDi)添加到列表L4中,最后将SKIDi作为结果返回.

⑥签密询问:当敌手AI对(M,IDS,IDR)发起签密询问时,若IDS=a,那么算法B可以利用a解决q-ABDHE问题;否则,算法B能够构造IDS的私钥,然后运行签密算法并返回相应的门限签密C=(C1,C2,C3,C4,C5,C6,T).
⑦解签密询问:当敌手AI对C发起解签密询问时,若IDR=a,那么算法B可以利用a解决q-ABDHE问题;否则,算法B从列表L4中查询接收者的私钥SKIDR,然后运行解签密算法恢复出消息m并把它发送给AI.
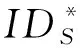
令s=(loggg′)fq+1(a),如果Z=e(gaq+1,g′),则有
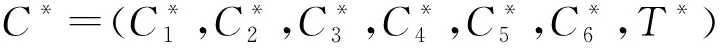
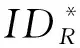
Guess:敌手AI输出b′作为b的猜测.如果b=b′,那么B输出Z=e(gaq+1,g′)作为q-ABDHE问题的解.证毕.
定理2 如若DBDH是困难问题,对于第二类攻击者AII,本方案满足适应性选择密文攻击下的不可区分性.
证明设敌手AII能够成功攻破本方案,则可以构造算法B,其可利用敌手AII解决DBDH问题,而这与DBDH是一个困难问题相矛盾.
输入算法B的DBDH问题实例(ga,gb,gc,h),其目标是判定等式h=e(g,g)abc是否成立.这里算法B模拟AII的挑战者C与其交互如下:

Phase1:敌手AII可如同定理1中那样进行询问,由于敌手AII知道主密钥,故无须进行部分私钥询问.此外,它不能够进行公钥替换询问.
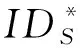
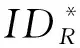
Phase2:敌手AII可如同定理1中那样进行询问.
Guess:敌手AI输出b′作为b的猜测.如果b=b′,那么B输出h=e(g,g)abc作为DBDH问题的解.证毕.
3.3 不可伪造性
定理3 如若q-SDH是困难问题,本方案在第一类攻击者AI攻击下满足存在不可伪造性.
证明如果敌手AI能够成功伪造一个有效的密文,则存在算法B,它可以利用AI解决q-SDH问题,而这与q-SDH是一个困难问题相矛盾.
输入算法B的q-SDH问题实例(g,ga,ga2,…,gaq),其目标是利用敌手AI计算(c,g1/a+c).这里算法B模拟AI的挑战者C与其交互如下:
Setup: 算法B如同定理1中那样构造系统参数,并将params发送给敌手AI,不同之处在于h2=g-u.
Attack:
①当敌手AI发起H1询问、用户公钥询问、用户私钥询问以及公钥替换询问时,算法B如同定理1中第一阶段那样进行响应.
②部分私钥询问:当对身份IDi的部分私钥DIDi进行询问时,如果IDi=a,算法B可利用a解决q-SDH问题;否则,算法B采取与定理1中相同的方式进行响应.
③签密询问:当对(M,IDS,IDR)发起签密询问时,若IDS=a,算法B可利用a解决q-SDH问题;否则,算法B采取与定理1中相同的方式进行响应.
④解签密询问:当敌手AI对C发起解签密询问时,若IDR=a,算法B可以利用a解决q-SDH问题;否则,算法B采取与定理1中相同的方式进行响应.

如果A-1=0,那么算法B将失败退出;否则,可以得到
则q-SDH问题的解为
证毕.
定理4 如若CDH是困难问题,本方案在第二类攻击者AII攻击下满足存在不可伪造性.
证明如果敌手AII能够成功伪造一个有效的密文,则存在算法B,它可以利用AII解决CDH问题,而这与CDH是一个困难问题相矛盾.
输入算法B的CDH问题实例(ga,gb),其目标是利用敌手AII计算gab.这里算法B模拟AII的挑战者C与其交互如下:
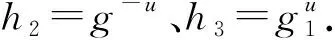
Attack:敌手AII可如同定理3中那样进行询问.由于敌手AII知道主密钥,故无须进行部分私钥询问.同时,它不能够进行公钥替换询问.

则有

4 性能分析
因双线性对运算的开销远大于群元素的其他计算开销,故这里只考虑双线性对的运算.假定门限签密方案中的门限值为t,成员总数为n.这里可通过对z0=e(g,g)和z1=e(g,h1)进行预计算来提高计算效率.
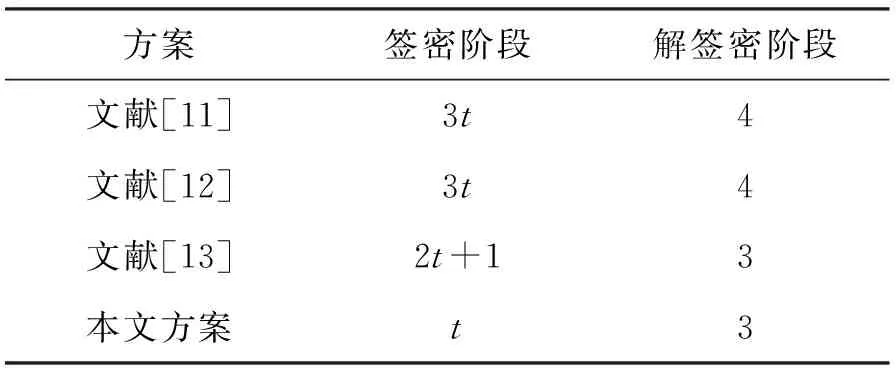
表1 门限签密方案的比较
通过表1对比可知,本文所提出的方案具有较低的计算开销.
5 结论
本文提出了一个安全且具有较高效率的无证书门限签密方案.如何设计具有特定应用背景的无证书密码方案,且具有较少的运算量和通信开销,是我们下一步将继续开展的工作.
