基于粒子群算法优化最小二乘支持向量机的网络安全态势评估

黄 东,李长彬

(钦州学院 数学与计算机科学学院, 广西 钦州 535000)

0 引言

网络技术已经成为人们生活中不可缺少的一部分,由于互联网的开放性，网络安全随之而来[1],被动防范策略无法满足人们对网络安全的要求，网络安全态势评估可对网络安全将来状态进行估计，成为网络管理领域研究中的重大课题[2].

传统网络安全态势评估模型采用专家系统构建，评估的准确性与专家知识库密切相关，导致评估结果不太科学、不可信[3-4].随后有学者基于统计学理论，提出了隐马尔可夫模型、模糊推理、贝叶斯网络的网络安全态势评估模型[5-8].但是在实际应用中，这些模型存在许多争论，网络安全态势评估结果的正确性饱受质疑[9].近些年，随着现代机器学习算法的不断发展，一些专家和学者将K近邻算法、神经网络、支持向量机等引入到网络安全态势评估中，如文献[10]提出了支持向量机的网络安全态势评估模型，利用支持向量机的非线性处理能力，描述网络安全态势变化的不确定和动态性[10].文献[11]提出K近邻算法和支持向量机相融合的网络安全态势评估模型，通过两者的优势互补，提高了网络安全态势评估正确率[11]，但是这些算法均存在一定的局限性，如神经网络易出现过拟合现象、支持向量机训练费时、K近邻算法分类结果不稳定等[12].最小二乘支持向量机(least square support vector machine， LSSVM)是一种新型的机器习算法，较好地解决了神经网络的过拟合缺陷以及支持向量机训练时间长等难题，在许多领域得到了成功应用[13].

为了获得更加理想的网络安全态势评估结果，本文提出一种粒子群优化(particle swarm optimization，PSO)算法和LSSVM的网络安全态势评估模型(PSO-LSSVM)，并通过具体仿真实验对模型性能进行测试.

1 最小二乘支持向量机及粒子群优化算法

1.1 最小二乘支持向量机

设训练样本为：T=(xi,yi),i=1,2,…,m;LSSVM通过f(·)拟合输入量和输出量之间的映射关系，即有：

f(x)=wΦ(x)+b,

(1)

式中，w称为权向量，b称为阈值[14].

基于经验风险最小化构造如下函数：

(2)

其中，L称为损失函数，其表达式为：

(3)

其中，ε是大于0的小数.

当学习样本有限时，根据结构风险最小化准则可选取非线性回归函数为：

(4)

根据“最大间隔”原理，LSSVM的非线性回归问题可以转化为求解以下函数规划问题：

(5)

其中，γ表示惩罚参数.

约束条件为：

(6)

其中：ξ，ξ*为两个松弛变量.

将上式转化为拉格朗日对偶问题求解，可解得：

(7)

其中：αi为拉格朗日乘子，K()称为核函数，并满足：

K(xi,xj)=(Φ(xi)·Φ(xj)).

(8)

本文选择高斯核函数作为LSSVM核函数，其定义如下：

(9)

在实际应用中，LSSVM性能与核函数及参数选择密切相关，γ越大，易出现过拟合现象；γ太小，易出现欠学习现象；σ过小、过大同样会出现过学习或欠学习现象.

1.2 粒子群优化算法

粒子群优化(PSO)算法是一种模拟鸟群捕食行为的群智能算法.在PSO算法的工作过程中，粒子通过跟踪局部极值(pbest)和全局极值(gbest)来调整自己飞行方向.

每一次迭代过程中，粒子的位置和速度更新方式[15]：

(10)

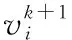
2 PSO-LSSVM的网络安全态势评估模型

2.1 参数对LSSVM的性能影响分析

选择一个两分类问题分析参数对LSSVM分类性能的影响，不同参数γ和σ值的分类正确率如图1和图2所示.从图1和图2可知，参数γ和σ对LSSVM的分类性能影响较大，二者之间互相关联，因此本文采用粒子群算法对γ和σ进行优化，获得更好的LSSVM的分类性能，从而提高网络安全态势评估的正确率.

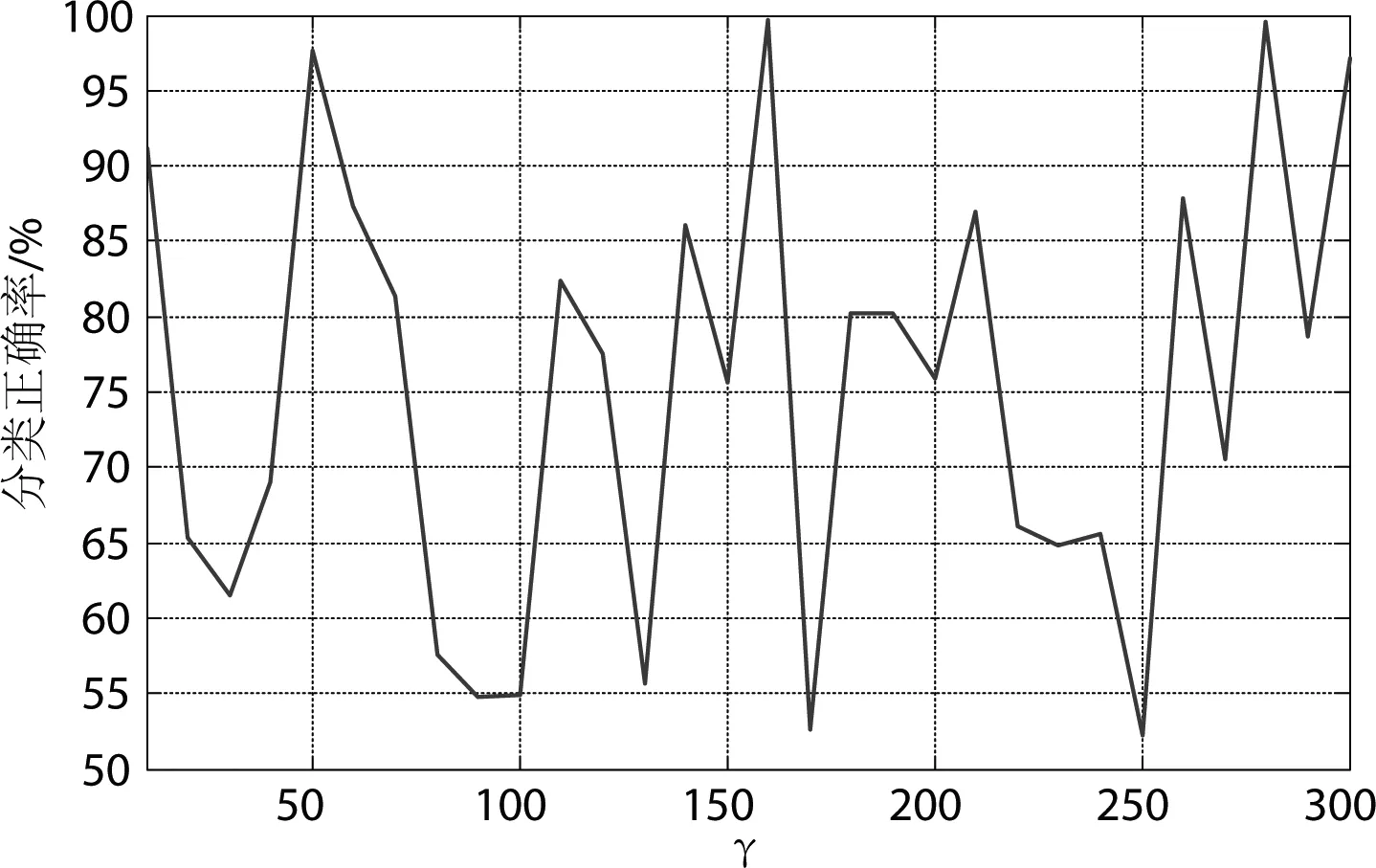
图1 γ与LSSVM的分类性能之间的关系

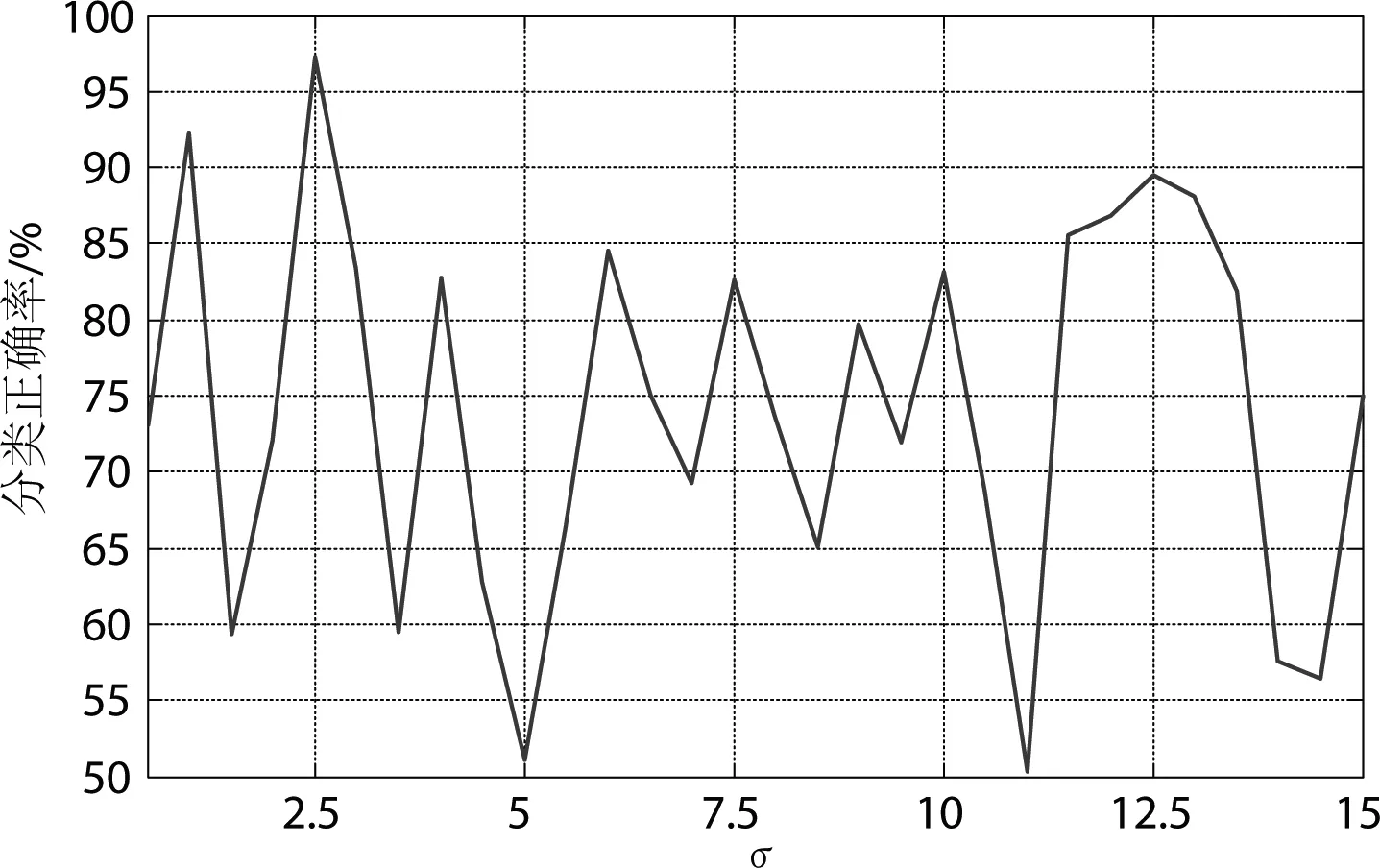
图2 σ与LSSVM的分类性能之间的关系

2.2 PSO-LSSVM的网络安全态势评估过程

(1) 收集网络安全态势历史样本，对样本进行归一化.

(2) 确定LSSVM参数γ、σ的取值范围，设置粒子群优化算法的相关参数.

(3) 采用随机方式产生粒子群，每一个粒子的位置向量代表一组γ、σ.

(4) 将网络安全态势训练样本输入到LSSVM学习，并采用每一组γ、σ计算网络安全态势评估的正确率，将其作为粒子的适应度值，并确定pbest和gbest.

(5) 确定更新粒子的速度和位置，产生新的粒子群.

(6) 计算新粒子群的适应度值，将每一个粒子的适应度值与其pbest比较，如果更优，则替代pbest.

(7) 将每一个粒子的适应度值与gbest比较，如果更优，则替代gbest.

(8) 如果满足终止条件，则停止参数寻优，输出最优γ和σ值，否则跳到步骤(3)继续执行.

(9)根据最优γ和σ值，建立网络安全态势评估模型.

3 PSO-LSSVM在网络安全态势评估的应用

3.1 数据来源

网络安全态势的评估指标为：报警数目(x1)，攻击源个数(x2)，攻击频率(x3)，时间重要程度(x4)，带宽占用率(x5);网络安全级别为：很低(0.01)、低(0.1)、中(1.0)、高(10)、很高(100)共5个级别，共获得100个数据，它们具体如表1所示.

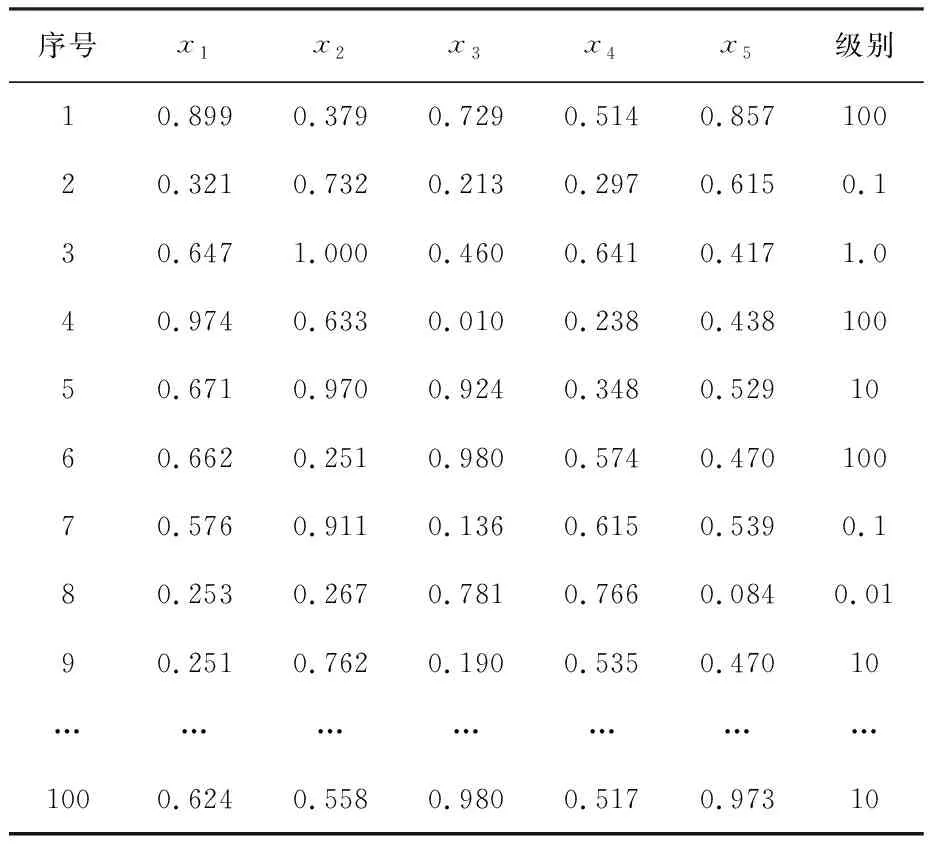
表1 采集的网络安全态势评估数据

3.2 结果与分析

选择遗传算法优化LSSVM(GA-LSSVM)、K近邻算法(KNN)以及BP神经网络(BPNN)进行对比实验,采用网络安全态势评估的正确率、误判率作为评价标准.

3.2.1 评估结果对比

采用粒子群算法优化LSSVM参数γ和σ，得到最优γ=125.70和σ=0.228，从而建立相应的网络安全态势评估模型，其与对比模型的评估正确率、误判率分别如图3和图4所示.

对图3和图4进行分析，可以得到如下结论：

(1) KNN、BPNN的网络安全态势评估正确率低,主要由于KNN算法要求样本分布比较均匀，BPNN要求样本数量比较大，而且网络安全态势评估是一种样本分布不均衡、小样本分类问题，因此易产生过拟合、评估结果不准确等难题.

(2) 相对于GA-LSSVM，PSO-LSSVM进一步提高了网络安全态势评估正确率，网络安全的误判率也有所改善，这主要由于相对于遗传算法，粒子群优化算法的搜索能力更强，找到了更加合理的LSSVM参数γ、σ值，获得了更加理想的网络安全态势评估结果.

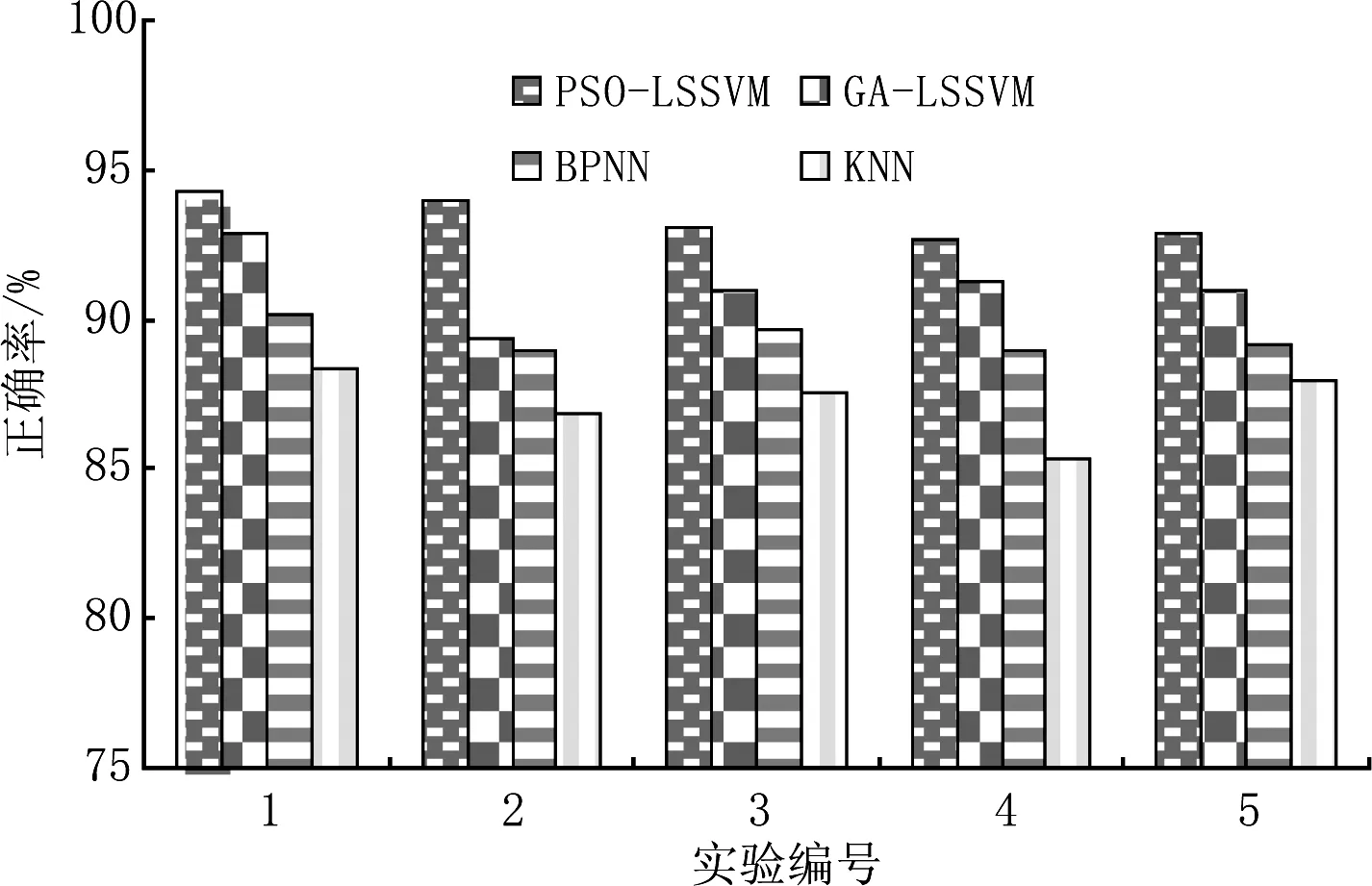
图3 各模型的网络安全态势评估正确率比较

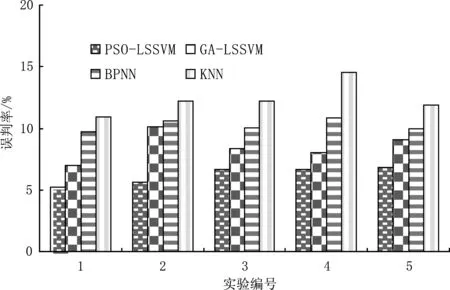
图4 各模型的网络安全态势评估误判率比较

3.2.2 建模及评估效率比

所有网络安全评估模型的建模时间和评估时间如图5所示.从图5可以看出，相对其他网络安全态势评估模型，PSO-LSSVM的建模时间和评估时间最少，加快了建模与评估速度，可以满足网络安全态势的在线、实时评估需求，因此，相对于其他网络安全态势评估模型，PSO-LSSVM的应用范围更广.

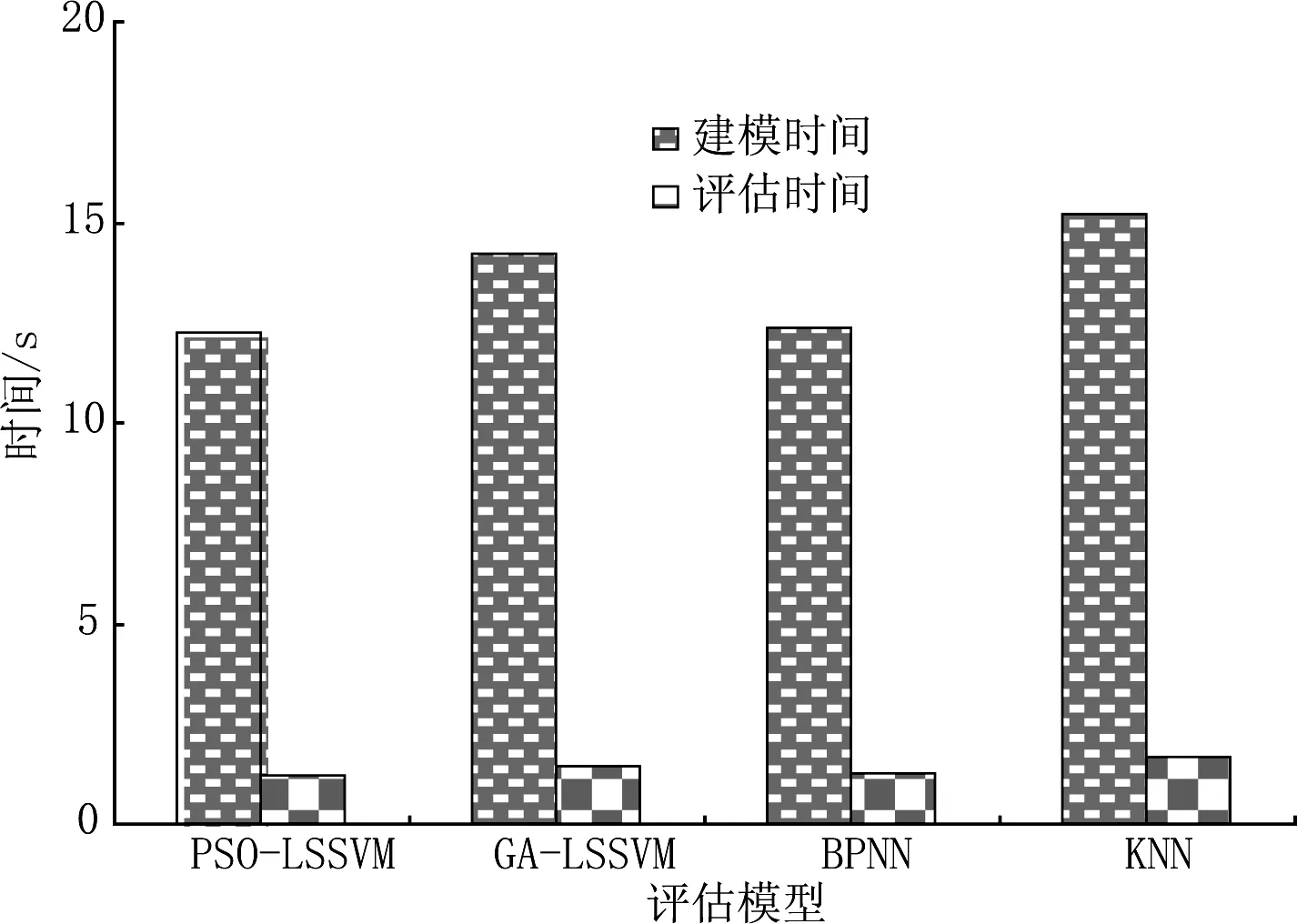
图5 各模型的网络安全态势评估效率比较

4 结语

针对网络安全态势变化的随机性、动态性，提出了一种PSO-LSSVM的网络安全态势评估模型.实验结果表明，PSO-LSSVM不仅获得了更加理想的网络安全态势评估结果，而且降低了计算复杂度，评估结果可以为网络管理人员提供有价值的参考信息.