支持矢量回归机的参数优化及在智能减压阀压力预测中的应用

童成彪　周志雄　周　源

1.湖南大学，长沙，410082 2. 湖南省特大口径电站阀门工程技术研究中心，长沙，410007



支持矢量回归机的参数优化及在智能减压阀压力预测中的应用

童成彪1,2周志雄1周源1

1.湖南大学，长沙，410082 2. 湖南省特大口径电站阀门工程技术研究中心，长沙，410007

摘要：智能减压阀可通过控制膜片缸压力实现出口压力的智能调节。膜片缸压力是智能减压阀控制器的控制目标，因此需要依据进口压力和出口目标压力对膜片缸压力进行预测。基于此，提出了基于人工化学反应优化算法的支持向量回归机(ACROA-SVR)参数优化方法，并将ACROA-SVR应用于智能减压阀膜片缸压力预测，采用实验数据将ACROA-SVR与基于遗传算法的SVR和传统SVR进行了对比，分析结果表明了ACROA-SVR的有效性和优越性。

关键词：人工化学反应；支持矢量回归机；参数优化；智能减压阀；回归预测

0引言

传统的自力式减压阀采用先导阀控制主阀的出口压力。先导阀是一个膜片式减压阀，其弹簧压紧量可通过人工调节螺母来改变，从而设定主阀的出口压力。智能型自力式减压阀(以下简称智能减压阀)采用膜片缸代替螺母施加压力来调节先导阀弹簧的压紧量。膜片缸压力受控制器的控制。控制器是一个内置单片机、集成电路、液压系统和控制软件的控制单元，通过控制器改变膜片缸压力从而达到智能调节出口压力的目的。基于控制系统建模的要求，根据先导阀进口压力和出口目标压力对膜片缸压力进行预测是必要的。然而，受到橡胶的超弹性、流体静压与动压的转换等复杂的流体动力学问题的限制，很难建立起进口压力、出口压力和膜片压力三者关系的精确数学模型，给膜片缸压力的预测带来困难。通过实验，可测得先导阀进口压力、出口压力、膜片缸压力之间的有限数量样本数据，因此希望能寻求到一种合适的预测方法，以样本数据建立的训练模型为基础，能根据工况中的进口压力和出口目标压力对膜片缸压力进行预测，再以预测的膜片缸压力作为控制器的控制目标，最终实现主阀出口压力的智能调节。

常用的模糊控制、人工神经网络、支持矢量回归机(support vector regression，SVR)等预测方法，都具有鲁棒性好、能够拟合非线性函数等特点。模糊控制器的建立大都依赖专家和操作者的知识经验，存在较大的主观性和随意性，很难获得满意的控制效果[1]。人工神经网络存在学习收敛速度慢、容易陷入局部极小点而无法得到全局最优解、训练精度较差等缺点[2]。SVR在解决非线性、小样本、高维模式识别以及局部极小等问题中具有许多特有优势[3]，其性能与核参数的选择密切相关，因此需要对SVR的参数进行优化。目前，常用的优化方法有遗传算法(genetic algorithm，GA)、粒子群优化等。然而，遗传算法存在编码、解码、遗传、变异、交叉等复杂操作，需要选择的参数很多[4]。粒子群算法在优化过程中容易出现局部极值、早熟收敛等问题[5-6]。人工化学反应优化算法(artificial chemical reaction optimization algorithm，ACROA)是一种新的自适应全局优化算法，具有鲁棒性好、输入参数少、计算量小、计算时间短等优点[7-9]。文献[10]将ACROA用于支持向量机参数的优化，并将优化后的支持向量机应用于机械故障的分类，取得了较好的结果。

本文将ACROA用于支持矢量回归机参数优化，提出了基于人工化学反应优化算法的支持矢量回归机(support vector regression based on artificial chemical reaction optimization algorithm，ACROA-SVR)，并将其应用于智能减压阀压力预测，通过实验数据与基于遗传算法的SVR(GA-SVR)和传统SVR进行了对比。在不同训练样本数的情况下，ACROA-SVR都可以得到最小的预测误差，表明了ACROA-SVR的有效性和优越性。

1人工化学反应优化算法

ACROA是一种自适应的优化算法，通过模拟化学反应过程来解决全局或局部搜索优化问题[9]。ACROA可以看成有N种不同化学反应的盒子，首先采用二进制或十进制方式对反应物进行编码，然后基于反应物浓度和电位来选择反应物。通过特定化学反应产生新的反应物之后，由目标函数更新反应物种群，当不再产生新的反应物或迭代次数达到设定的最大值时，终止算法。ACROA的具体步骤如下[7-9]：

(1)问题初始化。ACROA优化问题可概括如下：

minf(x)

s.t.xi∈Di=[li，ui]i=1，2，…，N

(1)

式中，f(x)为目标函数；xi为决策变量；N为决策变量的个数；Di为第i个决策变量的取值范围；ui、li分别为第i个决策变量的上下界。

(2)反应物初始化。采用Karci提出的均匀总体法[6]将初始反应物均匀地初始化到可行的搜索空间中。首先，设定两种反应物R0=(u1，u2，…，un)，R1=(l1，l2，…，ln)，n为决策变量的维数，此时，分裂因子k=1。然后不断增加分裂因子，k=2时，从R0、R1中产生反应物R2、R3：

R2=(ru1，ru2，…，run/2，rln/2+1，rln/2+2，…，rln)

(2)

R3=(rl1，rl2，…，rln/2，run/2+1，run/2+2，…，run)

(3)

其中，r为随机数，0≤r≤1。k=3时，可以产生另外23-2=6种反应物，依此类推。如果反应物的个数M小于设定的初始种群的大小P，就增加k，产生更多的反应物；M≥P时，就产生了具有P个反应物的初始种群。

(3) 化学反应优化。ACROA中所用到的两种基本化学反应是单分子反应和多分子反应。

对于单分子反应，设反应物R=(r1，r2，…，rn)，ri∈[li，ui]，分解反应产生新的反应物为

(4)

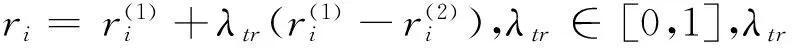
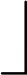
(4)反应物种群更新。化学反应优化结束后，将新生成的反应物代入目标函数进行计算，如果得到的结果更优，则将新生成的反应物代替原反应物，从而实现反应物种群更新。

(5)检查结束条件。每完成一次优化，迭代次数加1，当满足最大迭代次数时，终止ACROA，否则重复步骤(3)、步骤(4)。ACROA的流程如图1所示[10]。

图1　ACROA流程图

文献[10]采用ACROA对支持向量机参数进行优化，并用UCI benchmark数据集中的通用数据Iris、thyroid验证优化后的支持向量机的分类性能，结果表明，ACROA-SVR在分类精度和效率上都优于其他方法。本文将ACROA用于SVR参数的优化，并将ACROA-SVR方法应用于智能减压阀的压力预测。

2基于ACORA的SVR参数优化

支持矢量机回归的基本思想是通过非线性映射φ将数据x从原始非线性空间Rn映射到高维特征空间F，并在这个特征空间进行线性回归，即

f(x)=ω·φ(x)+b

(5)

式中，ω为超平面的法向量；b为阈值。

这样，在高维特征空间的线性回归便对应于低维输入空间的非线性回归。对于某一训练集T={(x1，y1)，(x2，y2)，…，(xl，yl)}，其中，l为样本的数目，xi∈Rn，yi∈R，i=1，2，…，l。支持矢量机回归的基本方法如下：

(1)选择适当的精度参数ε和惩罚参数C。

(2)选择损失函数e(x，y，f)，定义经验风险：

(6)

损失函数有多种，本文采用最常用的线性ε不敏感损失函数[11]。

(3)选择适当的核函数k(xi，xj)=φ(xi)φ(xj)；核函数的种类较多，有多项式函数、RBF函数、Sigmoid函数等[12]。本文采用的是径向基核函数：

k(xi，xj)=exp(γ‖xi-xj‖2)

(7)

式中，核参数γ>0。

(4)将下式分别对ω和b求微分并令它们等于零:

(8)

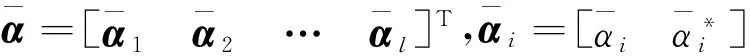
(5)构造回归模型[13]

(9)

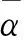
(10)

(11)

对SVR结果精确度影响最大的参数是惩罚参数C和核参数γ[11-12]，本文将采用ACROA对这两个参数进行优化，提出ACROA-SVR的方法，其流程如图2所示。

图2　ACROA-SVR流程图

为了验证ACROA-SVR的优越性，采用一个简单的正弦信号y=sinx对该方法和SVR、GA-SVR进行仿真对比分析，采样频率为20 Hz，预测数据点数为8，结果如表1所示。从表1可以看出，在不同的样本数据情况下，ACROA-SVR的训练时间最短，而且预测平均误差最小，验证了ACROA-SVR可以有效地应用于数据预测。

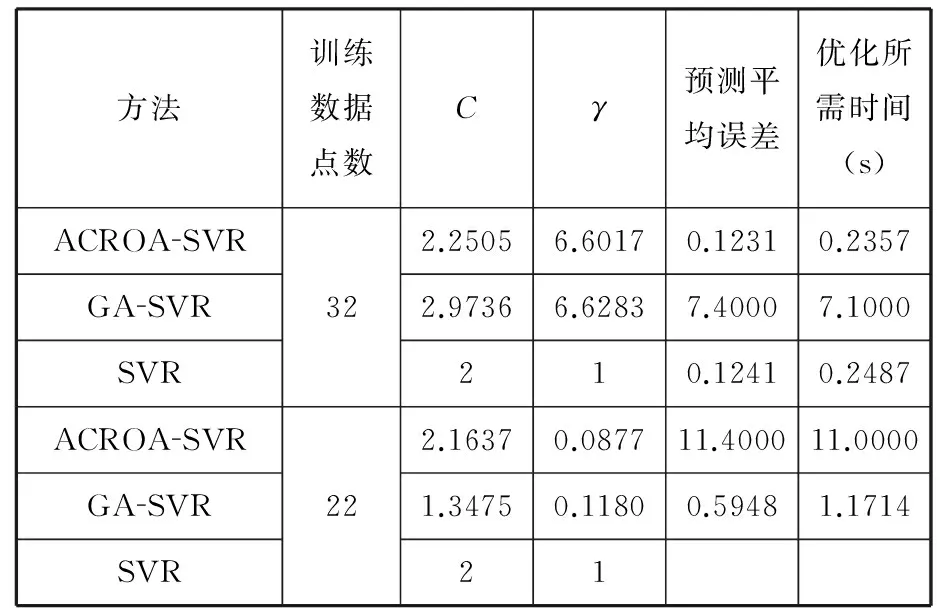
表1　仿真信号预测结果对比

3应用实例

构建试验平台，分别在4种不同的工况(阀后针形阀全开、阀后针形阀顺时针转2圈、阀后针形阀顺时针转4圈、阀后针形阀顺时针转5圈)下各测得10组先导阀阀前压力、阀后压力、膜片缸压力数据。表2列出了每种工况下的2组样本数据。在每种工况下，将8组数据作为训练数据，将剩余2组数据作为预测数据。为了进行对比，ACROA-SVR和GA-SVR中迭代次数均取为20，初始种群数目均取为20。优化的结果见表3、表4。从优化结果可以看出，相对于GA-SVR、SVR，ACROA-SVR优化所需时间短，而且预测平均误差最小，验证了ACROA-SVR的优越性。

在上述对比的基础上，保持预测数据个数不变，逐渐减少训练样本数据的个数，分别计算出ACROA-SVR、GA-SVR、SVR的平均误差，见表5。从表5可以看出，随着训练数据减少，ACROA-SVR预测的平均误差仍然是最小的，由此可以看出，样本数量的变化并不影响ACROA-SVR相对于GA-SVR和SVR的优越性。值得提出的是，随着训练样本的减少，虽然训练时间相对缩短，但ACROA-SVR的预测误差是增大的，因此，在实际应用中，应根据具体情况选择合适的训练样本数量。

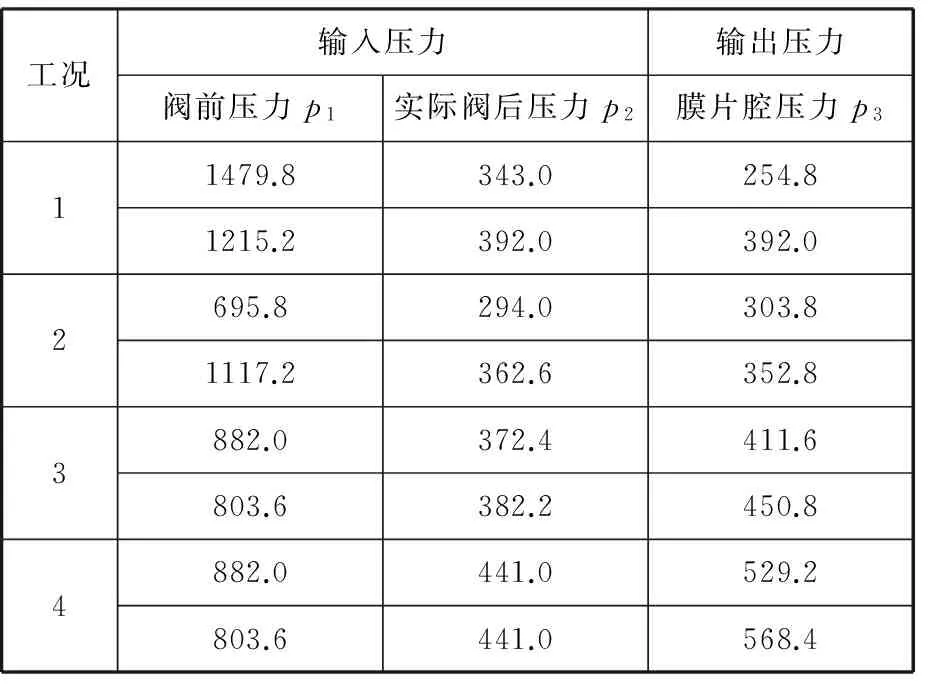
表2　部分原始数据　kPa

表3　优化结果

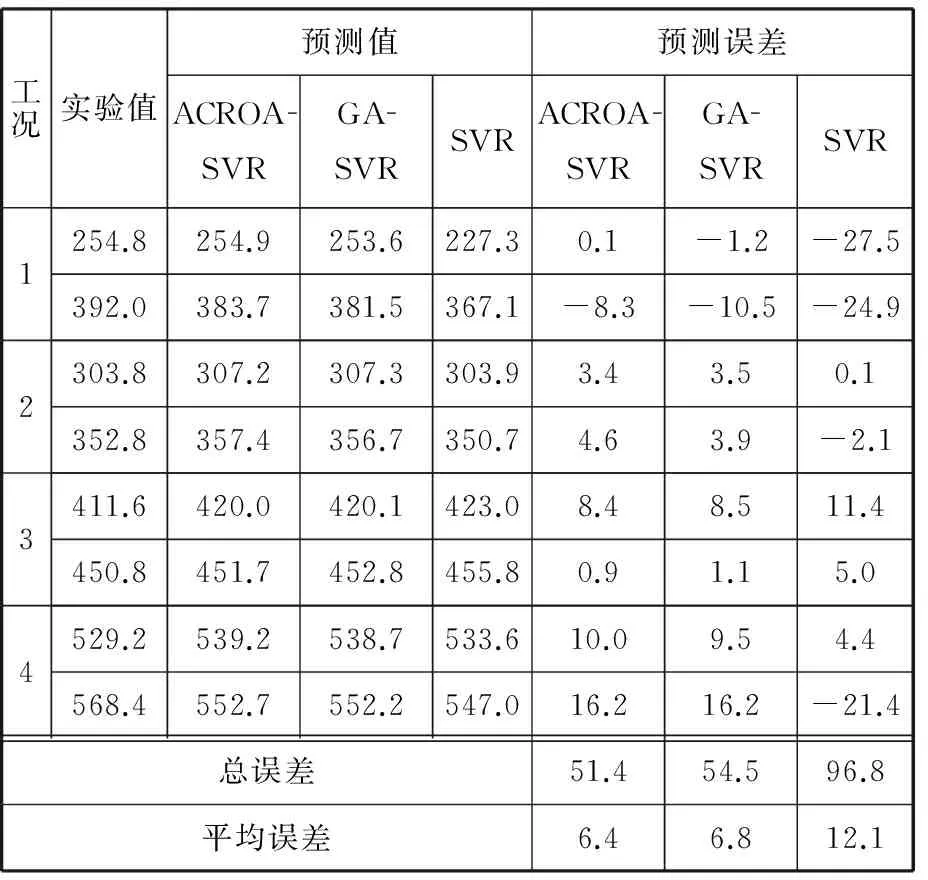
表4　预测结果及误差对比　kPa

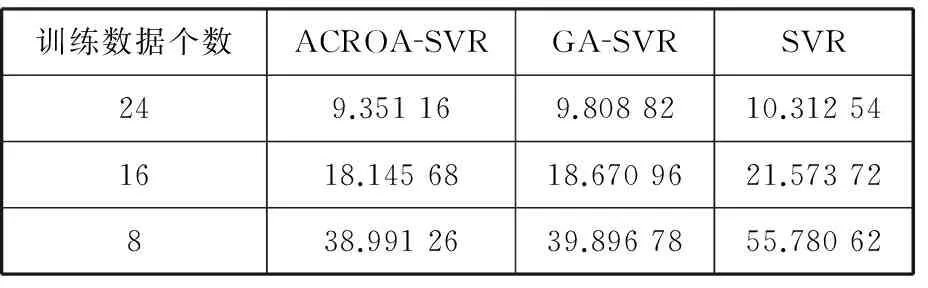
表5　减少训练样本的预测平均误差　kPa

4结语

提出了基于人工化学反应的支持矢量回归机参数优化方法，并将其应用于智能减压阀的压力预测。采用实验数据将ACROA-SVR、GA-SVR、SVR进行了对比，结果表明，在训练样本数不同的情况下，ACROA-SVR都能得到最小的预测误差，基于人工化学反应的支持矢量回归机能可以应用于智能减压阀的压力预测。

参考文献：

[1]师五喜. 未知多变量非线性系统自适应模糊预测控制[J].控制理论及应用,2011,28(10):1399-1404.

ShiWuxi.AdaptiveFuzzyPredictiveControlforUnknownMultivariableNonlinearSystems[J].ControlTheory&Applications, 2011, 28(10):1399-1404.

[2]陈波，潘海鹏，邓志辉. 基于PSO优化RBF神经网络的反应釜故障诊断[J].中国机械工程,2012,23(18): 2204-2207.

ChenBo，PanHaipeng，DenZhihui.ApplicationofPSO-basedRBFNeuralNetworkinFaultDiagnosisofCSTR[J].ChinaMechanicalEngineering,2012,23(18): 2204-2207.

[3]程军圣，于德介，杨宇. 基于支持矢量回归机的Hilbert-Huang变换端点效应问题的处理方法[J]. 机械工程学报, 2006, 42(4): 23-31.

ChengJunsheng，YuDejie，YangYu.ProcessMethodforEndEffectsofHilbert-HuangTransformBasedonSupportVectorRegressionMachines[J].ChineseJournalofMechanicalEngineering, 2006, 42(4): 23-31.

[4]陈果. 基于遗传算法的支持向量机时间序列预测模型优化[J]. 仪器仪表学报, 2006, 27(9): 1080-1084.

ChenGuo.OptimizingofSupportVectorMachineTimeSeriesForecastingModelParametersBasedonGeneticAlgorithms[J].ChineseJournalofScientificInstrument, 2006, 27(9): 1080-1084.

[5]王维刚，刘占生. 多目标粒子群优化的支持向量机及其在齿轮故障诊断中的应用[J]. 振动工程学报, 2013, 26(5):743-749.

WangWeigang，LiuZhansheng.SupportVectorMachineOptimizedbyMulti-objectiveParticleSwarmandApplicationinGearFaultDiagnosis[J].JournalofVibrationEngineering, 2013, 26(5):743-749.

[6]魏立新，王利平，马明明，等. 基于改进多目标粒子群算法的冷连轧规程优化设计[J]. 中国机械工程, 2015,26(9): 1239-1242.

WeiLixin，WangLiping，MaMingming，etal.OptimizationofTandemColdRollingScheduleBasedonImprovedMulti-objectiveParticleSwarmOptimizationAlgorithm[J].ChinaMechanicalEngineering, 2015,26(9): 1239-1242.

[7]AlatasB.ArtificialChemicalReactionOptimizationAlgorithmforGlobalOptimization[J].ExpertSystemswithApplications, 2011, 38(10): 13170-13180.

[8]AlatasB.ANovelChemistryBasedMetaheuristiOptimizationMethodforMiningofClassificationRules[J].ExpertSystemswithApplications, 2012, 39(12): 11080-11088.

[9]YangShida，YiYalin，ShanZhiyong.Gbest-guidedArtificialChemicalReactionAlgorithmforGlobalNumericalOptimization[J].ProcediaEngineering, 2011, 24: 197-201.

[10]罗颂荣，程军圣，HunglinhAO. 基于人工化学反应优化的SVM及旋转机械故障诊断[J]. 中国机械工程, 2015, 26(10): 1306-1311.

LuoSongrong，ChengJunsheng，HunglinhAO.SVMBasedonACROAandItsApplicationstoRotatingMachineryFaultDiagnosis[J].ChinaMechanicalEngineering, 2015, 26(10): 1306-1311.

[11]张超，陈建军，郭迅. 基于EMD能量熵和支持向量机的齿轮故障诊断方法[J]. 振动与冲击, 2010, 29(10): 216-220.

ZhangChao，ChenJianjun，GuoXun.AGearFaultDiagnosisMethodBasedonEMDEnergyEntropyandSVM[J].JournalofVibrationandShock, 2010,29(10): 216-220.

[12]ZhangXiaoli，ChenXuefeng，HeZhengjia.AnACO-basedAlgorithmforParameterOptimizationofSupportVectorMachines[J].ExpertSystemswithApplications, 2010, 37(9): 6618-6628.

[13]邓乃扬, 田英杰. 数据挖掘中的新方法——支持矢量机[M]. 北京：科学出版社, 2004.

(编辑张洋)

收稿日期：2015-10-10

基金项目：国家科技重点专项(2011ZX07412-001-02)

中图分类号：TN911；TH113

DOI：10.3969/j.issn.1004-132X.2016.14.015

作者简介：童成彪，男，1979年生。湖南大学机械与运载工程学院博士研究生，湖南省特大口径电站阀门工程技术研究中心高级工程师。主要研究方向为阀门的智能控制。发表论文10余篇。周志雄(通信作者)，1953年生。湖南大学机械运载工程学院教授、博士研究生导师。周源，男，1990年生。湖南大学机械与运载工程学院硕士研究生。

Parameter Optimization of Support Vector Regression and Its Applications to Pressure Prediction of Intelligent Pressure Reduce Valves

Tong Chengbiao1, 2Zhou Zhixiong1Zhou Yuan1

1.Hunan University,Changsha,410082 2.The Special Largest Size Valve Engineering Research Center of Hunan Province,Changsha,410007

Abstract：Intelligent pressure reduce valve might regulate the downstream pressure by controlling the diaphragm cylinder pressure. Diaphragm cylinder pressure was the control goal of pressure reduce valve intelligent controller, so it was necessary to forecast the diaphragm cylinder pressure according to upstream pressure and downstream pressure. Thus, the parameter optimization method for SVR was proposed based on artificial chemical reaetion optimization algorithm(ACROA-SVR). Furthermore, the ACROA-SVR was applied to the pressure prediction of the diaphragm cylinder pressure herein. By analyzing the experimental data, ACROA-SVR was compared with SVR based on genetic algorithm and traditional SVR. The efficiency and superiority of ACROA-SVR was shown by the analyzed results.

Key words:artificial chemical reaction(ACR); support vector regression(SVR); parameter optimization; intelligent pressure reduce valve; regression prediction