基于NURBS直纹面拟合敏感点的空间凸轮侧铣刀轨算法优化

胡东方　张文博

河南科技大学，洛阳，471003



基于NURBS直纹面拟合敏感点的空间凸轮侧铣刀轨算法优化

胡东方张文博

河南科技大学，洛阳，471003

摘要：基于NURBS直纹面拟合敏感点的空间凸轮侧铣刀轨算法优化原理，提出了拟合误差敏感点的选择方法，根据NURBS曲面重构的原理，将曲面曲率最值点和拟合误差最大点定义为理论加工刀轨曲面误差敏感点。利用曲率敏感点，在理论非等径刀轨曲面规划离散网格，得到初始数据点。通过最小二乘优化方法重构NURBS刀轨直纹面，再根据误差敏感点定义的等参数曲线来调整刀轨直纹面形状。构建了理论加工误差模型，并通过实例的仿真计算和数值模拟说明了该算法的有效性。

关键词：空间凸轮；侧铣加工；敏感点；NURBS直纹面；形状调整

0引言

空间凸轮的廓形误差会缩短其使用寿命。提高空间凸轮的精度可以有效减小凸轮在运行过程中的振动，提高凸轮机构运行的平稳性。对于大批量生产的空间凸轮，在精加工阶段通常采用共轭创成法进行加工[1]，即刀具与被加工凸轮共轭创成复现滚子与凸轮的共轭运动，采用的刀具与滚子几何特征参数完全相同，这样就保证了所生成的廓面与滚子完全啮合。这种方法加工出的凸轮除了由内外螺旋线螺旋角不一致而造成的原理误差外，并没有其他误差，因此可制造出较高精度的凸轮。等径加工存在的缺陷是必须保证刀具的半径与滚子半径严格一致，刀具需要专门定制，在小批量生产时加工成本会变得很高。因此，非等径加工是常用的空间凸轮小批量生产的加工方式，即采用半径小于滚子半径的刀具加工空间凸轮廓面。

近年来，学者们针对凸轮的非等径侧铣加工刀轨优化问题，从刀具与工件的局部几何关系和NURBS直纹面整体逼近两个方面进行了研究。文献[2]根据局部刀具与凸轮的接触线几何关系计算出加工最佳切触点，减小了理论加工误差；文献[3]综合侧铣点位偏置算法的优点，建立局部刀位搜索模型来确定最优刀位点；文献[4]简化了刀具与凸轮接触线几何关系求解模型，提出了一种自适应误差补偿算法；文献[5]根据NURBS曲面重构原理，利用最小二乘法从整体上提高了理论加工精度；文献[6]对理论非等径刀轨曲面进行了插值反算，并利用遗传算法从整体上对刀轨进行了优化。从误差控制效果和算法实现效率来看，整体直纹面逼近算法的理论误差相对较小，也无需过多考虑局部优化过程中存在的刀具干涉问题，因此，从总体上来看，NURBS直纹面整体逼近算法要优于局部几何优化方法。

现有直纹面逼近算法都只运用了NURBS最基本的算法原理，鲜见对NURBS拟合算法深层次应用的研究。因此笔者提出一种基于NURBS直纹面拟合敏感点的侧铣刀轨优化算法，利用NURBS曲面重构原理的多种数学性质构建误差控制模型，减小空间凸轮非等径侧铣加工的理论误差。

1NURBS直纹面拟合

直纹面是通过位于两条准线之间的直线做连续运动而形成的曲面，其准线S(u)的NURBS表达式为[7-8]

(1)

式中，u为准线的定义域，u∈[0,1]；Wi为权因子； Ni,k(u)为k次规范B样条基函数；di为准线的控制顶点位置矢量(简写为控制顶点，下同)。

在不影响直纹面的逼近的前提下，可对式(1)进行简化，设定两条NURBS准线的次数和节点数均相同。由于理论刀轨面数据点之间权重相等，取NURBS曲面所有权因子W=1。3次NURBS在CAM中应用广泛，因此采用3次NURBS方程对刀轨曲面进行重构，取k=3。因此NURBS直纹面的两条准线S1(u)和S2(u)可表示为3次B-Spline形式：

(2)

直纹面方程可根据两条准线定义为

S(u,v)=(1-v)S1(u)+vS2(u)

(3)

v∈[0，1]

将式(2)代入式(3)，可得NURBS直纹面表达式：

(4)

Ri,k；j,l(u,v)=

式中，di,j为NURBS表达式的权因子；Ri,k;j,l(u,v)为NURBS表达式的基函数；Wi,j为直纹面S(u,v)的权因子；Nj,l(v)为NURBS直纹面母线上的基函数，其中l=1，表示直纹面母线次数为1。

2敏感点对NURBS拟合约束

NURBS拟合曲面生成过程中，需要从初始理论曲面获得初始数据点，然后利用数据点拟合NURBS曲面。理论曲面离散数据点的采样算法和拟合出的曲面形状对理论加工误差有直接影响。一般情况下，理论NURBS曲面初始数据点的采样算法采用等参数离散法，拟合曲面采用NURBS插值反算方法。通过分析NURBS曲面的拟合算法原理可知，NURBS重构过程中会出现“弓高”误差，利用等参数离散插值反算重构算法求得的NURBS曲面，其拟合误差会随着曲率的增长而逐步提高，并在曲率最值点达到最大。从NURBS曲面重构原理上来看，曲率最大点就是误差最大点，即曲面曲率与曲面加工误差有着直接的对应关系[9]。因此可将曲率最值点与误差最大点统一定义为拟合误差敏感点[10]，在敏感点处施加约束来控制NURBS刀轨直纹面拟合误差。

2.1非等径刀轨曲面推导式及其性质

常用的求解刀轨曲面上任意点曲率的算法通过联立刀轨曲面坐标公式，得到该点周围小范围区域内其他若干离散数据点的坐标，将这些离散的数据点坐标代入曲率公式得到该点曲率的近似解。这种方法既无法求得刀轨曲面任意点曲率的准确数值解，也不能建立曲率与数据点离散模型的直接数学关系。为了从整体上构建NURBS直纹面拟合误差控制模型，将理论刀轨曲面数据点离散算法建立在曲率约束的数学模型基础上，使得拟合误差与数据点离散形成直接的对应关系。

空间圆柱凸轮通过滚子和运动导杆来控制末端从动件的运动，按运动形式可将空间圆柱凸轮可分为直动凸轮和摆动凸轮。以空间摆动圆柱凸轮为例，其轮廓设计方法是，将凸轮的轮廓曲线展开成矩形平面，然后按照平面凸轮轮廓的设计方法求得展开的轮廓曲线，最后将平面轮廓曲线转换到三维空间，生成等槽深的轮槽。基于以上分析可推导出一种新的空间凸轮的数学建模方法：先通过轮廓方程得到滚子的理论二维运动曲线，然后将运动曲线首尾相接进行“缠绕”，这样就生成了等径刀具的运动曲线，再通过“扫掠”曲面的方法进行等径刀轨曲面的构造，如图1、图2所示。基于这种原理得到等径刀轨曲面后，通过等距面偏置得到非等径刀轨曲面方程，从而简化非等径刀具轨迹面的求解。根据滚子轴线轨迹面表达式可知其为直纹面，等径刀轴轨迹面为滚子轴线轨迹面，非等径刀轴理论轨迹面为滚子轴线轨迹面的等距偏置曲面，令等径刀具(滚子)半径、非等径刀具半径分别为R和r，则刀轨等距面偏置距离值Δr=R-r。

图1　运动曲线缠绕

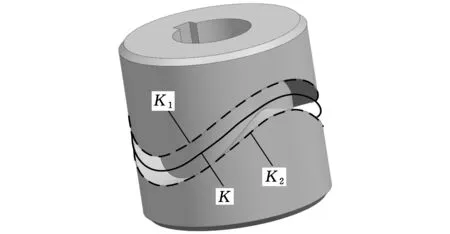
图2　扫掠生成圆柱凸轮

凸轮理论运动曲线展开线K上点si(xi，yi)的坐标计算公式为[11]

(5)

凸轮理论运动曲线展开线上的始末点s0、sn坐标为(x0，y0)和(xn，yn)；(xB，yB)为曲线K1或K2上任意点的坐标；λ=±1，取正号代表(xB，yB)为曲线K1上任意点的坐标，取负号代表(xB，yB)为曲线K2上任意点的坐标；α为滚子的瞬时压力角。

式(5)中参数xi、yi、α为未知量，可消去未知量α，使式(5)只含有未知量xi、yi，那么就可将式(5)改写为yi=f(xi)形式，这样就将凸轮的设计曲线与凸轮的理论运动曲线公式联系起来了。

设在凸轮外径上的si到s0的转角为θ，则θ=(xi-x0)/Rb。令Rb为空间凸轮的半径，Rb=(xn-x0)/(2π)，xi∈[x0，xn]。将滚子运动展开线转换至三维坐标系，得到等径刀具(滚子)外侧轴心运动曲线(等径刀轨直纹面导线)S(θ)在三维空间中的表达式：

S(θ)=(x(θ),y(θ),z(θ))=(Rbsinθ,Rbcosθ,yi)

(6)

根据等径刀轴轨迹面为直纹面的性质可知，S(θ)为等径刀轴直纹面的导线方程，对于导线上任意一点si，其沿母线方向矢量为l，则该点处等径刀轴直纹面母线l(θ)几何表达式为

l(θ)=(x(θ),y(θ),z′(θ))=(Rbsinθ,-Rbcosθ,0)

(7)

将其转化为切矢为参数方程的形式，根据式(6)、式(7)及直纹面性质可得到等径刀轨直纹面R0(θ，w)的几何表达式：

R0(θ，w)=S(θ)+wl(θ)

(8)

式中，w为直纹面母线。

根据式(8)及等距偏置面性质得到非等径刀轨曲面R(θ，w)的几何表达式：

R(θ，w)=R0(θ，w)+Δrn

(9)

式中，n为等距偏置曲面之间的法向矢量。

将式(9)改写成曲面第一、第二表达式形式：

RⅠ(θ，w)=Edθ2+2Fdθdw+Gdw2

(10)

RⅡ(θ，w)=Ldθ2+2Mdθdw+Ndw2

(11)

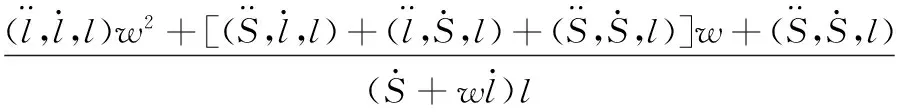
式中，E、F、G、L、M、N为理论非等径刀轨曲面的曲面第一、第二表达式中的参数。

根据式(10)、式(11)，可得非等径刀轨曲面的高斯曲率K*和平均曲率H*：

(12)

(13)

式中，k1、k2为非等径刀轨曲面的主曲率。

2.2基于曲率敏感点的离散路径规划

基于曲率敏感点的自适应规划思想对数据点取样网格进行规划[12]，具体步骤如下：

首先根据式(12)、式(13)得到理论刀轨曲面任一点主曲率k1、k2，然后定义刀轨曲面上任意一点的弯曲度：

(14)

根据高斯曲率和平均曲率公式 ，可将式(14)转化为

(15)

定义形状函数：

(16)

令非等径刀轨曲面SR={R(θ，w)| (θ，w)∈D0}，D0是参数θ和w的定义域。根据形状函数r(c)，假设SR离散采样点个数为P，定义采样点下标的集合D={1，2，…，P}。由于r(c)为能够反映曲面SR特征变化的形状函数，在D0上获得基于曲率敏感点的点集V={(θi，wi) |i∈D}使给定的P个抽样点能够表示曲面SR的特征。定义一个领域系统N={Ni|i∈D}，Ni是点(θi，wi)的相邻点的索引，其中i∉Ni。如果i∈Nj，j∈Ni，Ni可定义为网格四领域，则离散点(θi，wi)的最符合曲率的分布位置满足：

∑r(qj)(qi-qj)=0

式中，qi为第i次离散后点集的离散程度；qj为第j次离散后点集的离散程度，且j=i+1。

虽然非等径刀轨曲面的曲率演化规律能够在最终生成的网格上反映出来，但生成的网格形状散乱，不利于下一步基于NURBS直纹面的重构，所以需要对最终的网格数据进行分析和处理。形状函数r(c)在某点处的值越大，该点相邻部分在等参数条件下的形状变化越剧烈，即离散网格对曲率的“敏感度”越高。为了保留了刀轨面的几何特征，也使生成的网格更加规则，以便于NURBS曲面重构，可采用“曲率敏感点”方式，即将曲率敏感点作为约束条件，以曲率最大的点为有效数据点生成过该点的u、v坐标网格线。算法实现过程如下。

将自适应迭代后采集的数据点改写为的矩阵形式：

式中，a为等参数w曲线上离散得到的数据点个数；b为等参数θ曲线上离散得到的数据点个数。

矩阵同列数据点的参数w相同，同行数据点的参数θ相同。对于第i行的数据点，基于曲率敏感点规划后取坐标点为

(θi,wj)={(θi,wj)|k(θi,wj)=

由式(9)可得离散网格上对应等参数θ的网格线方程：

R(θi,w)=R0(θi,w)+Δrn=S(θi)+wl(θi)+Δrn

(17)

对于第nj列的数据点，基于曲率敏感点规划后取坐标点为

(θi,wj)={(θi,wj)|k(θi,wj)=

由式(9)可得离散网格上对应等参数w的网格线方程：

R(θ，wj)=R0(θ，wj)+Δrn=

S(θ)+wjl(θ) +Δrn

(18)

3基于误差敏感点的等参数曲线约束下NURBS曲面的形状调整

3.1基于最小二乘法的刀轨面初步拟合

最小二乘优化逼近方法是利用理论非等径刀轨曲面离散的数据点，通过最小二乘法构造一个NURBS直纹面来逼近理论非等径刀轨曲面。通常情况下，NURBS刀轨曲面拟合需要将等距偏置曲面离散的数据点沿着基准直纹面法向矢量方向进行投影，得到相应参数值后，再对基准直纹面进行逼近来获得所需NURBS曲面[13]。而空间凸轮的刀轨数据点是基于理论非等径刀轨曲面的离散点，理论非等径刀轨曲面就是最优基准面，因此可直接对理论非等径刀轨曲面进行逼近得到NURBS刀轨曲面。我们首先对曲面上采集的z+1个离散数据点Cij(θi，wj)进行双向累积弦长参数化，其中z+1=ab，得到NURBS拟合所需参数化数据点(ui*,vi*)，(ui*,vi*)为离散数据点参数化生成的NURBS参数序列值，i*=0,1,…,z。将(ui*,vi*)代入式(4)得到S(ui*,vi*)。为使NURBS直纹面对理论非等径刀轨曲面的整体逼近效果达到最优，应使NURBS直纹面到理论非等径刀轨曲面的距离最小，因此可利用最小二乘法即以NURBS直纹面到刀轨曲面上所有离散点的距离平方和最小为目标构造逼近目标函数：

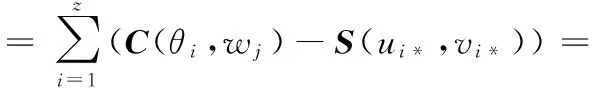
(19)

式中，X为控制顶点矢量；Φ为节点向量；C为理论非等径刀轨曲面上离散的数据点。

根据式(19)求解出实际NURBS刀轴轨迹面S(u，v)，其直纹面母线对应的为刀具轴心线。逼近法的理论加工误差为

δ=‖C(θ,w)-S(u,v)‖

(20)

3.2基于误差敏感点的等参数曲线的形状变化约束解算

为减小拟合曲面误差，可基于最小二乘拟合刀轨直纹面的最大误差点(该点拟合误差值为δmax)建立误差约束模型，改变拟合NURBS刀轨直纹面的局部形状，进行拟合误差的控制[14]。由式(4)可知，NURBS拟合曲面形状与控制顶点、权重因子和节点矢量有关，根据之前对敏感点与曲率、误差关系的分析，可建立基于误差敏感点约束的数学模型，进一步减小理论非等径刀轨直纹面拟合误差。

通过调整NURBS拟合曲面的形状，使拟合曲面在误差敏感点处与理论曲面重合，以此控制最大误差和相邻区域误差[15]。凸轮等径刀轨直纹面上对应的最大误差点为Cz(θz，wz)，可根据过该点的滚子直纹面母线lz的法矢nz，将lz沿nz方向偏置Δr，偏置后的曲线设为Ls，将曲线Ls作为目标约束曲线，则该曲线的等参数样条表达式为

(21)

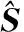
假设形状改变后的NURBS直纹面为

(22)

式中，S(u，v)为形状改变前的NURBS直纹面；εi,j为NURBS直纹面形状调整矢量。

我们通过约束条件下建立优化模型的方法来确定调整矢量εij。参照文献[15]可设优化模型的目标函数为

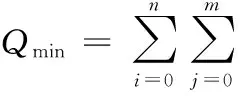
(23)

拉格朗日方程为

(24)

式中，λ*为拉格朗日乘数。

根据式(24)分别对参数λ*、εi,j求偏导得

(25)

消去参数λ*后，可得εi,j的显式表达式：

(26)

通过式(26)可以得到εi,j，将εi,j代入式(22)得到改变形状后的NURBS刀轨直纹面。

3.3基于NURBS拟合敏感点的临界条件

NURBS非等径刀轨直纹面初步拟合结果(最小二乘法拟合得到的曲面)的优劣可从两个方面(最大误差δmax和误差满足比例σ)进行判断，设δz和σm为判定条件。若拟合曲面的最大误差值δmax过大，则会造成在NURBS拟合直纹面敏感点算法调整形状后，拟合刀轨直纹面局部形状变化剧烈，这不利于在加工过程中对刀具姿态和进给速度进行精确的控制；若误差满足比例值σ过小，则会造成实际加工出的凸轮不能满足使用需求。

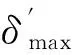
3.4刀轴参数的获得

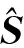
4基于NURBS拟合敏感点的空间凸轮侧铣刀轨算法实现方法

根据以上的分析，可以得出基于NURBS拟合敏感点的空间凸轮侧铣刀轨算法实现流程，如图3所示，具体步骤如下：

(1)利用本文算法建立精确的凸轮零件模型，根据获得的凸轮滚子轴线轨迹面得到理论非等径刀轨曲面。

(2)根据基于敏感点(曲率极值)算法获得理论刀轨曲面的数据点网格，并根据曲率最值点进行网格规化。

《孟子·离娄上》云:“爱人不亲，反其仁；治人不治，反其智；礼人不答，反其敬——行有不得者皆反求诸己，其身正而天下归之。”不反躬自省用人环境“短板”，进而排解“亡牢”问题，而妄图用“补羊”的办法解决“亡羊”问题，显属本末倒置舍本逐末。其结果必然是，小洞不补大洞吃苦，东边打鱼西边放生。

(3)利用最小二乘法对NURBS刀轨直纹面进行初步拟合，设置初步拟合最大误差临界值δ1、比例误差临界值δ*和误差满足比例临界值σm，计算NURBS直纹面初步拟合误差的最大值δmax和误差值小于δ*的数据点个数以求得误差满足比例σ，利用δ1和σm判断NURBS刀轨直纹面初步拟合的效果。若满足设定条件则进入步骤(4)；若不满足则返回步骤(2)，增加离散数据点个数。

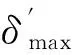
(5)输出满足要求的刀轨。

图3　敏感点算法流程图

5计算实例与仿真实验对比

为了验证本文算法的有效性，设计如下仿真实验：首先针对同一圆柱凸轮的同一工作廓面的非等径加工刀轨曲面，使用不同离散方法进行数据点采集，通过不同算法对曲面进行拟合重构，计算曲面的拟合误差并进行分析。

现加工一个空间摆动圆柱滚子凸轮，已知从动滚子半径R=10 mm，凸轮半径Rb=80 mm，滚子轴心运动展开线为正弦曲线，分度期转角为180°。凸轮模型根据滚子轴线直纹面生成的非等径理论刀轨曲面如图4所示。

图4　非等径理论刀具轨迹面

(1)首先分别基于等参数法和基于曲率敏感点法生成理论非等径刀轴轨迹面数据点离散网格，得到理论非等径刀轨直纹面的600个离散数据点。离散结果以及曲率分布如图5～图7所示，可看出基于敏感点规划离散网格可在理论刀轨曲面曲率较大的区域取到更多的点。

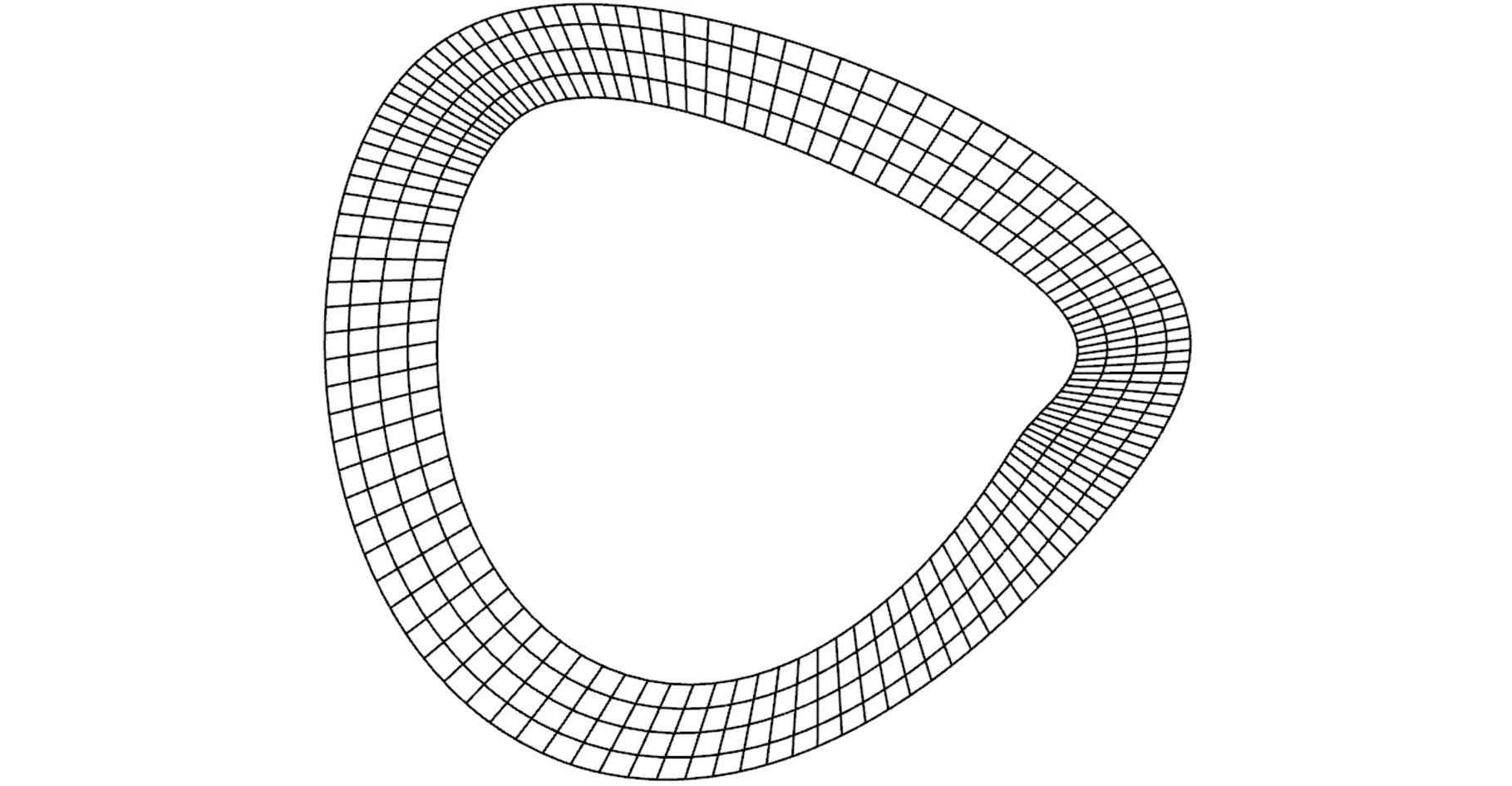
图5　基于等参数法刀轴轨迹面离散的网格

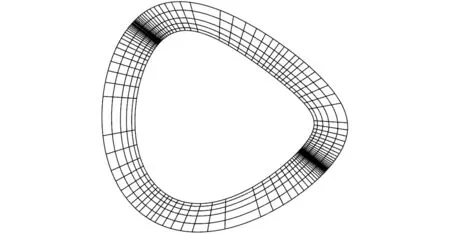
图6　基于敏感点刀轴轨迹面离散的网格

图7　理论刀轨面曲率分布云图

(2)根据算法进行拟合误差进行仿真分析，取加工立铣刀半径为9 mm，分别利用等参数最小二乘法(利用等参数离散法获得初始数据点，利用最小二乘法拟合刀轨直纹面)、敏感点最小二乘法(利用曲率敏感点自适应离散法获得初始数据点，利用最小二乘拟合刀轨直纹面)、敏感点拟合修正法(利用敏感点最小二乘法获得拟合刀轨直纹面，基于误差敏感点调整刀轨直纹面形状)三种算法对刀轨曲面进行拟合。根据实际加工精度要求，设定加工误差临界值δ*=0.01 mm。若NURBS刀轨直纹面在某区域内的拟合误差δ≤δ*，则认为该区域拟合误差足够小，刀轨逼近精度能够满足实际加工的精度要求，仿真结果图上用浅色表示此区域；反之则认为拟合误差过大，用深色表示。仿真结果如图8～图10所示，可以看出基于NURBS拟合敏感点算法能够获得最好的曲面逼近效果。

图8　基于等参数最小二乘法的拟合面误差分布图

图9　基于敏感点最小二乘法拟合面误差分布图

图10　基于NURBS拟合敏感点修正法拟合面误差分布图

(3)分别利用三种算法对刀轨曲面进行拟合，在中线(直纹面母线等参数二分点所在曲线)上对拟合误差进行数据采集，采集分度区间为0°～90°，对应的非等径刀具运动理论展开线的波谷和波峰作为采集区间的起始点和终点，所采集10个数据点的等分区间大小相同，在三种方法下拟合刀轨曲面的误差波动情况如图11所示。

图11　三种方法理论加工误差分布图

根据图11可得，敏感点修正算法对刀轨直纹面误差控制能力优于敏感点最小二乘法，敏感点最小二乘法优于等参数最小二乘法，误差敏感点拟合修正算法在曲率较大的区域能够较好地控制拟合误差，并能够有效减小最大刀轨拟合误差。但在曲率较小的区域，敏感点修正算法误差控制能力并不优于其他两种算法，这是由于该算法在曲率较小的区域获得的数据点较少，降低了算法在该区域的误差控制能力。

(4)利用三种算法，对不同半径立铣刀加工的拟合误差进行计算，得到最大加工理论误差结果，如表1所示。

表1　最大加工理论误差δmax

通过表1可以看出，在使用不同半径立铣刀时，NURBS拟合敏感点算法的拟合误差小于敏感点最小二乘法拟合误差，敏感点最小二乘法拟合误差小于等参数最小二乘法拟合误差。

6结论

(1)根据NURBS曲面重构原理，提出了一种减小NURBS直纹面拟合误差的方法。定义理论非等径刀轨面上曲率的最值点和误差最值点为敏感点，利用敏感点建立误差约束算法模型，对空间凸轮侧铣刀轨直纹面的拟合误差进行了控制，提高了空间凸轮理论非等径加工的精度。

(2)在凸轮理论刀轨曲面敏感点计算过程中，提出了一种基于运动曲线表达式的空间凸轮非等径理论刀轨曲面的推导算法。该算法简化了刀轨曲面表达式的推导过程，并能精确计算出非等径刀轨曲面上任意点曲率的数值，为进一步研究空间凸轮刀轨曲面的相关性质提供了算法依据。

(3)根据本文算法设计了相关模拟实验，通过数值仿真计算，验证了基于NURBS拟合敏感点刀轨优化算法的有效性，为减小NURBS曲面重构误差提供了理论依据。

参考文献：

[1]YanHS，ChenHH.GeometryDesignandMachiningofRollerGearCamswithCylindricalRollers[J].Mechanism&MachineTheory，1994，29(6)：803-812.

[2]尹明富，赵镇宏. 弧面分度凸轮单侧面加工原理及刀位控制方法研究[J].中国机械工程，2005，16(2)：127-130.

YinMingfu，ZhaoZhenhong.StudyonOne-sideMachiningPrincipleandToolPathControlMethodoftheGloboidalCam[J].ChinaMechanicalEngineering，2005，16(2) ：127-130.

[3]孔马斌，胡自化，李慧，等.基于等距曲面的弧面凸轮单侧面数控加工刀位优化算法[J].机械工程学报，2008，44(11)：277-282.

KongMabin，HuZihua，LiHui，etal.NewCutter-locationOptimizationAlgorithmandErrorAnalysisforFive-axisFlankMillingofIntegralImpeller[J].JournalofMechanicalEngineering，2008，44(11)：276-282.

[4]葛荣雨，冯显英，王庆松. 弧面凸轮廓面非等径加工的刀位控制方法[J].农业机械学报，2010，41(9)：223-226.

GeRongyu，FengXianying，WangQingsong.CutterLocationControlMethodforUnequalDiameterMachiningofGloboidalCamSurface[J].TransactionsoftheChineseSocietyforAgriculturalMachinery，2010，41(9)：223-226.

[5]葛荣雨，冯显英，宋现春，等. 空间凸轮廓面侧铣加工及最小二乘优化刀位方法[J]. 中国机械工程，2007，18，(15)：1842-1845.

GeRongyu，FengXianying，SongXianchun，etal.AlgorithmofCutterPositionforSideMillingofSpatialCamBasedonLeastSquareOptimization[J].ChinaMechanicalEngineering，2007，18(15)：1842-1845.

[6]葛荣雨，冯显英，宋现春，等. 弧面凸轮非等径侧铣刀位计算与遗传算法优化[J]. 农业机械学报，2007，38(10)：132-135.

GeRongyu，FengXianying，SongXianchun，etal.CalculationofCutterPositionforUnequalDiameterMillingofGloboidalCamandOptimizationBasedonGeneticAlgorithm[J].TransactionsoftheChineseSocietyforAgriculturalMachinery，2007，38(10)：132-135.

[7]LesPiegl，WayneTiller. 非均匀有理B样条[M].赵罡，穆国旺，王拉柱，译.北京：清华大学出版社，2010.

[8]施法中.计算机辅助几何设计及非均匀B样条曲线[M].北京：高等教育出版社，2013.

[9]玄冠涛，邵园园，吕钊钦，等. 基于NURBS的空间分度凸轮廓面重构与仿真[J]. 农业机械学报，2012，43(6)：226-229.

XuanGuantao，ShaoYuanyuan，LüZhaoqin，etal.ProfileReconstructionofSpatialIndexingCamandSimulationBasedonNURBS[J].TransactionsoftheChineseSocietyforAgriculturalMachinery，2012，43(6)：226-229.

[10]赖金涛，傅建中，沈洪壵，等. 基于NURBS曲面敏感点的曲面检测测点优化[J]. 浙江大学学报(工学版)，2015，49(7)：1201-1207.

LaiJintao，FuJianzhong，ShenHongyao，etal.MeasuringPointsOptimizationinMachiningErrorInspectionBasedonReconstructionofNURBSControlPointsDrivenbySensitivePoints[J].JournalofZhejiangUniversity(EngineeringScience)，2015，49(7)：1201-1207.

[11]石永刚，吴映芳.凸轮机构设计与创新应用[M].北京：机械工业出版社，2007.

[12]LiSZ.AdaptiveSamplingandMeshGeneration[J].Computer-AidedDesign，1995，27(3)：235-240.

[13]宫虎，曹利新，刘健，等. 数控侧铣加工非可展直纹面的刀位整体优化原理与方法[J]. 机械工程学报，2005，41(11)：134-139.

GongHu，CaoLixin，LiuJian，etal.GlobalOptimizationofPositioningStrategyforNCFlankMillingUndevelopableRuledSurfaces[J].ChineseJournalofMechanicalEngineering，2005，41(11)：134-139.

[14]王益，赖金涛，傅建中，等. 基于NURBS控制点重构的加工误差在机测量方法[J]. 浙江大学学报(工学版)，2014，48(10)：1781-1787.

WangYi，LaiJintao，FuJianzhong，etal.On-machineMeasurementofMachiningErrorBasedonReconstructionofNURBSControlPoints[J].JournalofZhejiangUniversity(EngineeringScience)，2014，48(10)：1781-1787.

[15]HuSM，LiYF，JuT.ModifyingtheShapeofNURBSSurfaceswithGeometricConstraints[J].Compute-AidedDesign，2001，33(12)：903-912.

(编辑张洋)

收稿日期：2016-02-01

基金项目：国家自然科学基金资助项目(51475146)；河南省教育厅重大科技攻关项目(13A520232)

中图分类号：TH132.47

DOI：10.3969/j.issn.1004-132X.2016.14.013

作者简介：胡东方，男，1967年生。河南科技大学机电工程学院副教授。主要研究方向为虚拟产品设计与开发。 获河南省科技进步奖二等奖 1项、三等奖1项。出版专著1部。发表论文 30余篇。张文博，男，1989年生。河南科技大学机电工程学院硕士研究生。

Flank Milling Cutter Path Optimization Method in Spatial Cam Machining Based on Reconstruction of NURBS Ruled Surface Driven by Sensitive Points

Hu DongfangZhang Wenbo

Henan University of Science and Technology,Luoyang，Henan，471003

Abstract:A new method to improve the tool path accuracy of frank milling was proposed based on the sensitive points affecting the NURBS ruled surface reconstruction for cam machining. The approach for the surface reconstruction was analyzed, and the curvature extreme points and the points with the maximum path error were defined as the sensitive points. The original data points was obtained by the adaptive sampling mesh planned by the curvature extreme points. Based on the least square method, the shape of the ruled surface reconstructed was modified by the constraint curve defined by the error sensitive points. At last, the numeral calculation and simulation experiments of the theoretical machining error model show the effectiveness of the algorithm.

Key words:spatial cam; flank milling; sensitive point; NURBS ruled surface; shape modification