多数者博弈模型演化分析

孙　康，全宏俊

(华南理工大学物理系，广东广州510641)



多数者博弈模型演化分析

孙康，全宏俊

(华南理工大学物理系，广东广州510641)

摘要：为研究经纪人行为策略对社会经济复杂系统的影响，本文在少数者博弈模型的基础上提出多数方获胜的基本多数者博弈模型以及演化多数者博弈模型。采用多主体建模方法，模型中的众多经纪人被赋予有限理性，他们可以选择自己的最优策略或者调整策略概率来竞争有限资源，演化到稳态后也能表现出人类社会系统所独有的现象。在基本少数者博弈中，当模型中的游戏规则变为多数方获胜时，得到的基本多数者博弈模型可以更快演化到稳定状态。并且在历史记忆长度m较小的时候系统资源利用率较高，随着m增大资源利用率逐渐降低，最终与经纪人随机选择得到的结果一致。而演化多数者博弈模型的资源利用率则不受m影响，因此在m较大时，引入演化能提高资源利用率。同样的系统参数，随机初始条件不同演化多数者博弈模型经纪人概率也有可能分布在p=0.5不同侧。同时发现，稳定后每时步平均获胜方人数与经纪人概率分布也有联系，在经纪人概率重置时采用不同的边界条件，得到的经纪人概率分布也不同。进一步分析演化多数者博弈模型系统资源利用率，发现经纪人新旧策略概率的相关程度r越大，概率分布越平坦，系统资源利用率越高。增加奖惩比R，也会影响经纪人概率分布，资源利用率也会提高。

关键词：行为策略；少数者博弈模型；基本多数者博弈模型；演化多数者博弈模型；有限理性

0引言

1997年D. Challet和ZHANG Yicheng在Arthur“酒吧模型”[1]的基础上提出了少数者博弈模型(MG)[2-5]。这是一个被高度重视并且广泛研究的多经纪人归纳博弈模型，模型的规则虽然简单，但它是一个典型的自适应复杂系统[6]，反映了许多社会与生态系统中多个体竞争有限资源并且少数方受益的现象。随后该模型风靡至今，得到显著发展。从MG到演化少数者博弈模型(EMG)[7]，再到引入模仿学习的少数者博弈模型[8-9]，以及近年来探讨的小世界网络上模仿学习的少数者博弈模型[10-11]等等。随着对少数者博弈模型的深入研究，该模型越来越复杂，也越来越接近现实。

生活中除了竞争有限资源的少数者博弈模型外，也存在主体行为策略是多数者策略(争取使自己处于多数方)的博弈模型。比如集市模型[12]，居民去赶集，相互之间没有任何交流与联盟，只有在赶集人数达到一定阈值的情况下，才能达到便利交易的预期。反之，则不如待在家里。又比如客户对社交软件的选择，自由市场中同一领域的社交软件只有抢占到更多用户才是胜者。因为对用户而言，随着使用该软件产品用户的增加，每个用户从此产品中获得的效用也会增加，才会吸引越来越多的经纪人选择该软件产品。相反，参与人数少的社交软件因为得不到理想的效用而使得用户愈发减少，最终使该软件产品淘汰。

1模型描述

1.1基本多数者博弈模型

将少数者博弈模型中的获胜规则改为每一轮博弈结束时人数大于总人数一半的一方为获胜方，其余规则保持不变，可得到基本多数者博弈模型。即，N(奇数)个经纪人，每个经纪人有s个策略，在每一时步都独立选择加入“0”或“1”，其记忆容量为m，知道最近m时步的二进制取胜方记录：u(t)={b(t-m)，…，b(t-2)，b(t-1)}，其中b(t)=“0”或“1”分别表示0方或1方取胜。每个经纪人按照自己某个策略做出选择后，人数多(少)的一方为获胜(失败)方，获胜(失败)方加1分(不加分)；并且给自己的s个策略评分(虚分)，如果某个策略预测了正确的获胜方，这个策略加1分，预测失败不加分；每一时步t，每个人根据t时步最近m次取胜方的记录u(t)，采用得分最高策略的预测来选择“0”或“1”，若得分最高的策略有2个以上，则随机选取其中的一个来做预测。

1.2演化多数者博弈模型

在N. F. Johnson和P. M. Hui等人提出演化少数者博弈模型(EMG)[7]基础上，改变经纪人的主体行为策略，可得到演化多数者博弈模型。即，考虑N(奇数)个经纪人组成的系统，每个经纪人事先知道最近出现的2m种不同历史(每个历史的长度为m比特)下取胜方的记录。所有经纪人拥有一个相同的策略，该策略在给定历史条件下对下一次取胜方的预测与该历史最近一次出现时的取胜方记录相同。所有经纪人随机指定一个概率p(i)(i=1，…，N)，0≤p(i)≤1，对给定的历史，每个经纪人以概率p(i)按策略的预测作出决定，或者以概率1-p(i)作出与策略预测相反的决定。当每个经纪人作出选择后，处于多数(少数)方的胜利(失败)，胜利方获得R分，失败方减1分，奖惩比为R。当某个经纪人财富小于给定的d(d<0)时，允许他在以p为中心、宽度为r的区间内重新按均匀分布随机挑选一个新的p(i)值，并将他的得分重新置零。采用反射边界条件，p(i)<0时，p(i)=-p(i)，p(i)>1时，p(i)=2-p(i)，以保证概率0≤p(i)≤1。在这一进化博弈模型中的经纪人可以不断地从过去的错误中学习，总是试图通过不断改变自身对策略的参照来寻求与社会的最好适应，而r则用来衡量经纪人在修正其概率时新旧概率的关联程度。

2结果与分析

2.1基本多数者博弈模型模拟结果

图1给出了m=10，s=2和N=1 001时的基本多数者博弈模型在某初始条件(初始策略，初始历史)下获胜方人数随时间变化的过程，通过数值计算发现获胜方人数很快(102级时步)达到稳定状态。而同样参数下的少数者博弈模型中获胜方人数往往需要在104级以上时步才开始趋于动态平衡。

图1　获胜方人数随时间演化Fig.1　Time evolution of the number of winners

对基本多数者博弈而言，由于经纪人总是采用虚分最高的策略，所以在经纪人的s条策略中，t-1时步被采用的策略(此策略虚分已经大于或等于其他策略)在t时步继续被采用的概率(可从t-1时步该策略加分和未加分两种情况考虑)往往会高于t-1时步未被采用的策略，从而使经纪人倾向于使用其s条策略中的某一条。当所有经纪人都采用较固定的优势策略时，容易形成固定的结果和固定的历史(可以从获胜方人数随时间的变化看出)，从而使系统快速达到稳定状态。

图2给出了经纪人平均成功率(所有经纪人成功博弈次数与博弈总次数比值的平均)随时间变化的过程，由多数者博弈规则，每一轮博弈中都有大于一半的经纪人获胜，经纪人平均成功率也就大于0.5，并趋于稳定。

图2　经纪人平均成功率随时间演化Fig.2　Time evolution of the average success rate of the agents

在少数者获胜规则下，稳态下某一方经纪人数的方差[13]越小则意味着系统资源利用率越高。然而多数者博弈模型并非零和博弈，在多数者博弈的同一回合中N个经纪人完全有可能都是获胜者。只是现实生活中，并非所有的经纪人都可以相互约定同时选择某一方。所以对多数者博弈模型而言，稳态下博弈中多数方平均经纪人数越接近N，则说明系统资源利用率越大。为此我们定义偏差θ：

(1)

其中T为系统稳定时所需要的时步，Δt是系统稳定后统计数据的时步。由图3可见，偏差θ∝N，并且由图4，对固定的m，有确定的相对偏差θ/N。所以θ/N表示一个与经纪人数目无关的参量，相对偏差反映实际获胜方人数与理想获胜方人数之间偏差与理想获胜方人数的比重，相对偏差越小说明越有效利用了市场资源。

图3　m=3和m=8时，θ和经纪人数目N的关系Fig.3　θ as function of N for m=3 and m=8

图4　经纪人数目N不同时，θ/N与m的关系Fig.4　θ/N as function of m for different values of N

图5给出了N=1 001，s=2条件下相对偏差与m的关系，图中每个数据点对应128次独立初始条件，在系统稳定后，再对500时步的结果进行统计平均。我们发现基本多数者博弈模型中的平均相对偏差随着m增大而增加，最终接近虚线所代表的经纪人随机作出选择得到的相对偏差。

在少数者博弈模型中，由于周期2动力学过程[14]和经纪人之间协作效应的竞争关系，用来衡量系统资源利用率的方差与m的关系不是单调的，在某个m0处系统协作性最好。然而多数者博弈模型最重要的一个特点是：大多数人的预期一致时，实际情况会按照人们的预期发展，所以多数者博弈模型中不存在周期2动力学过程，并且在多数者博弈模型的历史信息中同样存在着有助于预测多数方的信息。当m较小时，策略池也比较小，导致很多经纪人拥有相同的策略，由前文基本多数者博弈模型获胜方人数随时间演化过程分析，多数者博弈经纪人也更容易采用他手中某条固定的策略。因此在多数者博弈过程中，面对同样的历史，经纪人往往做出固定的决策，而这些固定的决策又形成了固定的历史，这时候策略和历史信息中预测胜利方的信息比较大。当m变大，策略池也变大，经纪人的策略不尽相同，历史也更多样化，所以预测胜利方的信息也就随m增大慢慢变少，最终接近随机选择得到的结果。

图5　N=1 001，s=2时，θ/N与m的关系Fig.5　θ/N as function of m for N=1 001 and s=2

图6　N=1 001，r=0.2，R=1，d=-4，θ/N与m的关系Fig.6　θ/N as function of m for N=1 001，r=0.2，R=1，d=-4

2.2演化多数者博弈模型模拟结果

图6给出了演化多数者博弈模型的θ/N与m的关系。图中的每个点对应32次独立初始条件，系统稳定后再对500时步进行统计平均，由图可见，演化多数者博弈模型的相对偏差与m无关。当m≥5时，演化多数者博弈模型可以比基本多数者博弈模型有着更高的资源利用率，即演化是有利的。

图7　经纪人概率分布Fig.7　Distribution P(p) of the p-values among the agents

图7a、图7b给出了演化多数者博弈模型概率分布，图7a、图7b有着相同的参数m=10，N=1 001，r=0.2，R=1，d=-4，但由于初始条件(初始概率、初始历史和初始策略)会有所区别，我们得到分布于p=0.5不同侧的“单峰分布”。

稳定后每时步获胜方人数

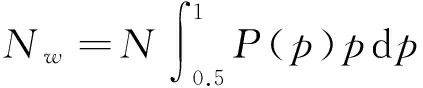
(2)

以图7a为例说明经纪人概率分布成因，在该次模拟初始概率随机分布下，共有510位p>0.5的经纪人，p>0.5的经纪人有较大的概率属于多数方，所以按公共策略决策的经纪人更容易在每一轮博弈中获胜，而p<0.5的经纪人更倾向于执行与公共策略相反的决策，从而在博弈中更容易处于少数方。对于p<0.5的某个经纪人而言，由于每一轮博弈的失败概率会大于获胜概率，随着时步t的增加，该经纪人因得分逐渐小于d而被淘汰，然后对概率进行重置。由反射边界条件可知，当新的p(i)<0时，p(i)=-p(i)，经纪人的概率只能向p>0.5的方向演化。一旦p(i)>0.5，经纪人i会因为获胜的概率大于失败的概率而很难被淘汰，同时也几乎失去演化动力停留下来。于是对整个系统而言，p=0.5右侧的经纪人逐渐被积累，最终形成我们看到的尖峰形分布。

演化多数者博弈模型的概率分布是以p=0.5为中点，随机分布在区间[0，0.5]或者区间[0.5，1]之间，并且演化多数者博弈模型稳定后的概率分布形状与经纪人概率重置时采用的边界条件有关。

图8　具有不同策略p的经纪人每时步平均得分Fig.8　Average rewards per round for the agents with different p-values

图8a表示的是对应图7a模拟中(图8b与图7b对应同一次模拟，初始随机概率p>0.5的经纪人数目为484人)演化到稳态后得到的拥有不同策略p的经纪人每时步平均得分，图中每个点对应一个经纪人，纵坐标对应着该经纪人每时步的平均得分，横坐标对应经纪人遵从策略的概率p。从图8a中可以发现，经纪人主要分布在p=0.5与p=0.65(与图7a中尖峰宽度一致)之间，初始概率越接近1的经纪人每时步的平均得分越多。而图8b中经纪人主要分布在p=0.5与p=0.35之间，初始概率越接近0的经纪人每时步的平均得分越多。

由图8a和图8b可以发现一个有趣的现象，正如现实生活中收益正比于风险，犹豫不决的经纪人(p=0.5左右的经纪人)只能获取较少的财富，采取极端行为往往会带来更大收益(收益最多的经纪人是那些初始概率为p=1或者p=0的经纪人)，但他们也承受着更大风险，一旦最初的极端选择使他们处于少数方，则必须经历更多次的淘汰和重置才能变成犹豫不决者存活下来。

N=1 001，m=10，R=1，d=-4时，通过模拟发现峰宽与经纪人修正错误概率时新旧概率的关联程度r的大小有关。随着r增大，图9 中尖峰的高度越低，但宽度越宽，经纪人向极端方向分布越平坦，同时由式(2)可知，获胜方平均经纪人数目也会增多，图10所示相对偏差也会减小。

图9　不同r值的概率分布Fig.9　Distribution P(p) of the p-values for different values of r

图10　不同r值θ/N与m的关系Fig.10　θ/N as function of m for different values of r

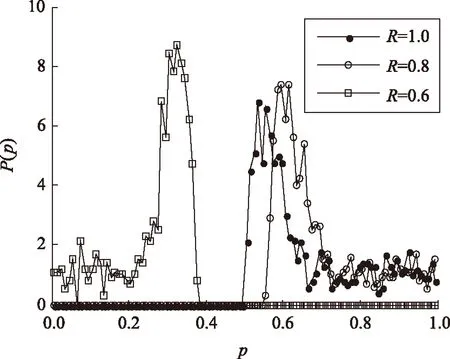
图11　不同R值的P(p)Fig.11　Distribution of P(p) for different values of R

图12　不同R值的θ/N与m的关系Fig.12　θ/N as funtion of m for different values of R

图11给出了N=1 001，m=10，d=-4，r=0.2时，不同奖励R下的概率分布P(p)，可以发现，当R<1时，由于获胜方在每一轮博弈中的得分变小，劣势状态下经纪人为避免淘汰不得不采用更极端的概率去接近p=0或p=1来提升自己的成功率，最终出现尖峰向两端移动的P(p)，R越小，移动趋势越明显。同时由图12可知，偏离方差θ/N也越小。

3结束语

多数者博弈除集市外还广泛存在于电信领域，最典型的例子为即时通讯软件、SNS社交网络服务等。多数者博弈也促成了“美团”、“滴滴”、“去哪儿网”等这些在快餐、打车、旅游行业抢先占有更多客户而兴起的公司，随着时代的发展，多数者博弈还将有更多的应用。

本文研究了多数方获胜的基本多数者博弈模型以及演化多数者博弈模型，分析了主体行为发生改变对系统演化状态的影响。我们发现主体行为策略是决定系统演化结果的关键因素，分析得到的结论对于解释现实生活中的一些现象以及控制一些实际系统里的合作程度有一定的参考价值。

参考文献：

[1]ARTHUR W B. Inductive reasoning and bounded rationality[J]. Am Econ Rev， 1994， 84(2)： 406-411.

[2]CHALLET D， ZHANG Yicheng. Emergence of cooperation and organization in an evolutionary game[J]. Physica A， 1997， 246(3-4)： 407-418.

[3]CHALLET D， ZHANG Yicheng. On the minority game：Analytical numerical studies[J]. Physica A， 1998， 256(3)： 514-532.

[4]ZHANG Yicheng. Toward a theory of marginally efficient markets[J]. Physica A， 1999， 269(1)： 30-44.

[5]杨城，孙世新，曾繁华，等. 非完备策略的少数者博弈[J]. 广西师范大学学报(自然科学版)，2006，24(4)： 235-238.

[6]HOLLAND J H. Emergence：From chaos to order[M]. Redwood City, CA： Addison-Wesley， 1998.

[7]JOHNSON N F， HUI P M， JONSON R， et al. Self-organized segregation within an evolving population[J]. Physical Review Letters, 1998, 82(16)： 3360-3363.

[8]FRANTISEK S. Harms and benefits from social imitation[J]. Physica A， 2001， 299(1-2)： 334-343.

[9]全宏俊， 汪秉宏， 罗晓曙. 模仿经纪人演化少数者博弈模型中的合作效应[J]. 中国科学院研究生院学报， 2003， 20： 101-104.

[10]CHEN Jiale， QUAN Hongjun. Effect of imitation in evolutionary minority game on small-word networks[J]. Physica A， 2009， 388(6)： 945-952.

[11]朱昌勇， 全宏俊. 演化少数者博弈在小世界网络上的信息传递效应[J]. 广西师范大学学报(自然科学版)， 2009， 27(4)： 11-14.

[12]纪明洁， 李红刚. 集市模型：少数者与多数者博弈演化分析[J]. 复杂系统与复杂性科学， 2012， 9(3)： 82-90.

[13]CAVAGNA A. Irrelevance of memory in the minority game[J]. Phys Rev E， 1999， 59： R3783-R3786.

[14]ZHENG Dafang， WANG Binghong. Statistical properties of the attendance time series in the minority game[J]. Physica A， 2001， 301(1)： 560-566.

(责任编辑王龙杰)

doi:10.16088/j.issn.1001-6600.2016.02.001

收稿日期：2015-12-15

基金项目：国家自然科学基金资助项目(11174083)

中图分类号：O414.2

文献标志码：A

文章编号：1001-6600(2016)02-0001-07

Evolutionary Analysis of the Majority Game

SUN Kang，QUAN Hongjun

(Department of Physics， South China University of Technology， Guangzhou Guangdong 510641， China)

Abstract:In order to study the influence of agents’ action strategies on the evolution of social economic system， the basic majority game and the evolutionary majority game in which agents prefer to stay in the majority are put forward on the basis of minority game. We build agent-based models，all the agents in the model are given bounded rationality， and they use their best strategy or modify their strategy probility each round in order to compete for finite resources. When evolving to stable state， phenomena which are unique to human society also occur. In the basic minority game， if agents in the majority are ruled winners, we get the basic majority game，and the game has higher resources utilization when the dimension of the strategy space， m， is smaller. As m gets larger， the utilization becomes lower， approaching that of the random choice game finally. While the utilization of evolutionary majority game isn’t affected by m， so，when m in the game is larger，the evolution is so perferable to improve the utilization of the system. With the same parameters in the game，different random initial conditions may cause different side of distribution of P(p) at p=0.5.The average number of winners each round is also found to be related to the distribution of P(p) at the same time. If we use different boundary conditions to reset agents’ strategy probabilities， we will also get different distribution of P(p). For further analysis of evolutionary majority game’s utilization， we find that the lager the parameter r which means the relation between agents’ old and new p，the flatter distribution of P(p) is，and the utilization also gets larger.At last， if we improve R representing the value of the prize-to-fine ratio， the distribution of P(p) will also be affected，resulted to a lager utilization of the game.

Keywords:action strategies；minority game； basic majority game； evolutionary majority game； bounded rationality

通信联系人：全宏俊(1958—)，男，湖南衡阳人，华南理工大学教授，博士。E-mail:hjquan@scut.edu.cn