颗粒团聚体在流场中的分散过程及力链演变*

麻向军　吴哲浩

(华南理工大学 聚合物成型加工工程教育部重点实验室∥聚合物新型成型装备国家工程研究中心， 广东 广州 510640)



颗粒团聚体在流场中的分散过程及力链演变*

麻向军吴哲浩

(华南理工大学 聚合物成型加工工程教育部重点实验室∥聚合物新型成型装备国家工程研究中心， 广东 广州 510640)

颗粒团聚体在加工过程中的分散效果直接影响了复合材料的综合性能.为研究颗粒团聚体在流场中的分散机理及动态细节，考虑颗粒间范德华力的作用，采用自主开发的三维颗粒离散元程序DEMix3D对分形结构团聚体在简单剪切流场中的变形和分散过程进行数值模拟，并分析团聚体在分散过程中细观结构的变化规律.研究发现：强弱力链交织形成了团聚体复杂的力链网络形态，强力链主要分布在力链网络内部，传递较大份额的流场作用力，弱力链传递小份额的流场作用力并充分分布在力链网络中；分散过程中团聚体力链结构的变化直接决定了颗粒的分散方式；当分散达到平衡状态时，碎片内的颗粒之间由于形成以强力链为主的紧密接触关系而不再分散.文中还根据碎片加权平均颗粒数的变化规律分析了流场强度对团聚体分散效果的影响.

颗粒团聚体；剥蚀；破碎；力链；离散元法

在复合材料加工领域，通常采用向聚合物基体或金属基体中添加细颗粒物质的方法来增强复合材料的各项性能，这些颗粒在基体中分散的均匀性直接影响了材料的最终性能.由于细颗粒表面能极大，在静电力和范德华力的作用下容易聚集形成颗粒团聚体，因此，对团聚体在流场中的分散机理以及动态细节进行研究，有助于更好地控制材料加工过程，优化加工工艺，设计高效的混合设备.

Powell等[1]对颗粒团聚体在剪切流场中的分散情况进行了研究，发现团聚体先变形成类似椭圆型的状态，而后颗粒才从团聚体中剥离下来.Higashitani等[2]报道了团聚体的两种典型分散方式——剥蚀和破碎，但并未提出颗粒脱离团聚体时究竟以何种方式进行分散的判定依据.近年来，数值模拟方法在研究团聚体分散过程中得到了广泛应用，由Cundall等[3]提出的离散元法(DEM)目前已成为颗粒体系运动和细观结构研究的有效工具，DEM能够提供颗粒的位移和接触力等详细信息，从而获得实验研究无法测量的物理信息.Hosseini等[4]利用离散元法模拟了二维颗粒团聚体在剪切、拉伸和混合流场中的分散行为，研究发现分散至平衡状态时团聚体的碎片尺度大小取决于流场强度以及团聚体的分形维数.麻向军等[5]基于二维离散元法模拟了团聚体在不同形式流场中的分散过程，并讨论了流场形式对其分散效率的影响.

团聚体细观尺度的力链结构是流场作用力的传递路径，对团聚体受力后力链结构的演变过程进行研究，能够更为深入揭示和理解团聚体的分散行为.目前，国内外学者从力链结构变化的角度对颗粒堆积、振动筛分等问题进行了大量的研究[6- 8]，但关于团聚体分散过程中力链的演变及其对颗粒分散行为影响的研究鲜见报道.文中采用自主开发的三维颗粒离散元程序DEMix3D模拟了DLA型颗粒团聚体在简单流场中的分散过程，从细观力学角度揭示颗粒团聚体的分散机理，分析团聚体力链结构的变化对颗粒分散方式的影响，并讨论流场强度对团聚体分散效果的影响.

1　颗粒团聚体分散运动的数学模型

1.1接触模型

离散元法将颗粒体系中的颗粒看成独立的离散单元，利用经典的牛顿第二定律，根据每一时刻各颗粒间的相互作用，计算团聚体中每个颗粒的平移运动和旋转运动，而后通过对时间的积分求得颗粒的位移，进而获得接触力和配位数等信息.由牛顿第二定律得到颗粒的运动方程：

(1)

(2)

式中：mi和Ii分别为颗粒i的质量、转动惯量；vi和ωi分别为颗粒i的速度和角速度；Fi和Mi分别为颗粒i所受的合力和合力矩，Fi和Mi表达式为

(3)

(4)

文中采用Hertz-Mindlin接触模型[10]，法向接触力与法向重叠量的关系为

(5)

式中，δn为法向重叠量，E*为等效弹性模量，R*为等效半径.

不考虑微滑移的影响，切向接触力与切向重叠量的关系为

(6)

式中，δt为切向重叠，G*为等效剪切模量.

1.2范德华力模型

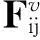
(7)

式中，A为Hamaker常数，h为颗粒表面间距.

1.3流体拖曳力模型

(8)

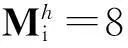
(9)

式中,η为流体黏度，Γ为速度梯度张量，Ω为涡度矢量.

对于纯剪切流场，

(10)

(11)

但是，这样的简化放大了团聚体中被周围颗粒完全包围或部分包围的颗粒所受到的拖曳力，为此引入有效系数ζ来考虑周围颗粒对流体拖曳力的屏蔽作用.三维空间中，半径相同的均质颗粒周围最多能够和12个颗粒发生接触.当某个颗粒与周围颗粒接触数量达到12时，则认为ζ=0，即该颗粒不受到流体拖曳力的作用；与11个颗粒接触时，取ζ=1/12；当颗粒不和其他颗粒接触时，则ζ=ζ-1

1.1.4模拟条件

采用扩散限制凝聚模型(DLA)生成三维颗粒团聚体，颗粒数目为500，分形维数为1.98，所生成的团聚体如图1所示.定义流场强度

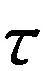
(12)

为研究流场强度对团聚体分散的影响，设定流场强度分别为100、300、500、700 和1 000Pa进行模拟计算，计算时步为1×10-10s，颗粒半径R为100nm，颗粒密度ρ为1 050kg/m3，Hamaker常数为1.3×10-20J，弹性模量E为1.39×10-9Pa，流体黏度η为0.01Pa·s.

图1　三维DLA团聚体

2　结果与讨论

2.1分散过程中团聚体的力链演变

颗粒物质具有典型的多尺度特征，微观尺度为组成颗粒体系的颗粒单体，宏观尺度为整个颗粒体系，细观尺度则是指颗粒单体间形成较为稳定的结构体，亦即力链[12].图2给出了流场强度为500Pa时团聚体的分散过程及力链演变过程，文中借鉴Sun等[13]提出的强力链判定准则，将接触力大于团聚体平均接触力的力链视为强力链，在力链网络中用粗线表示.

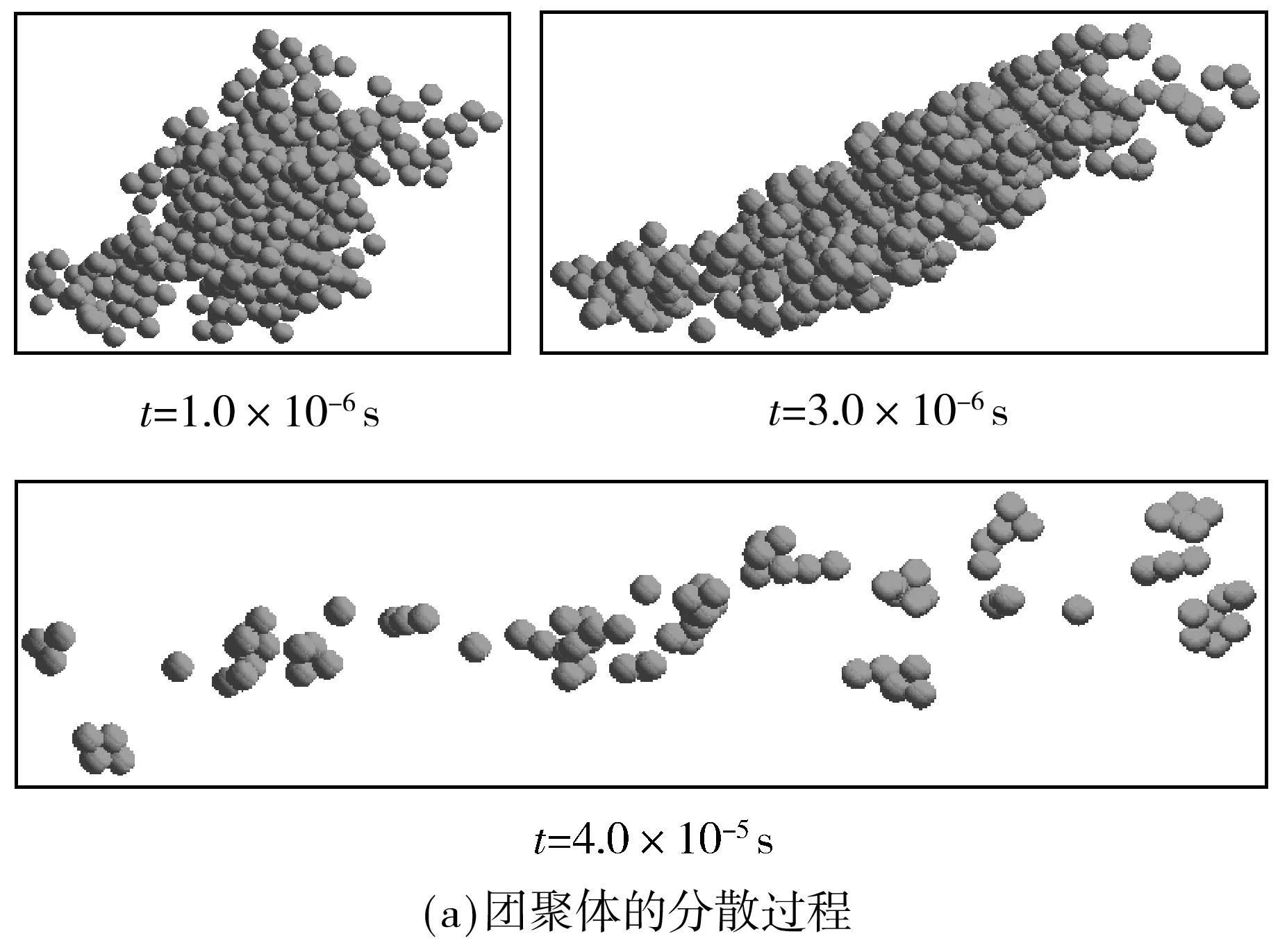
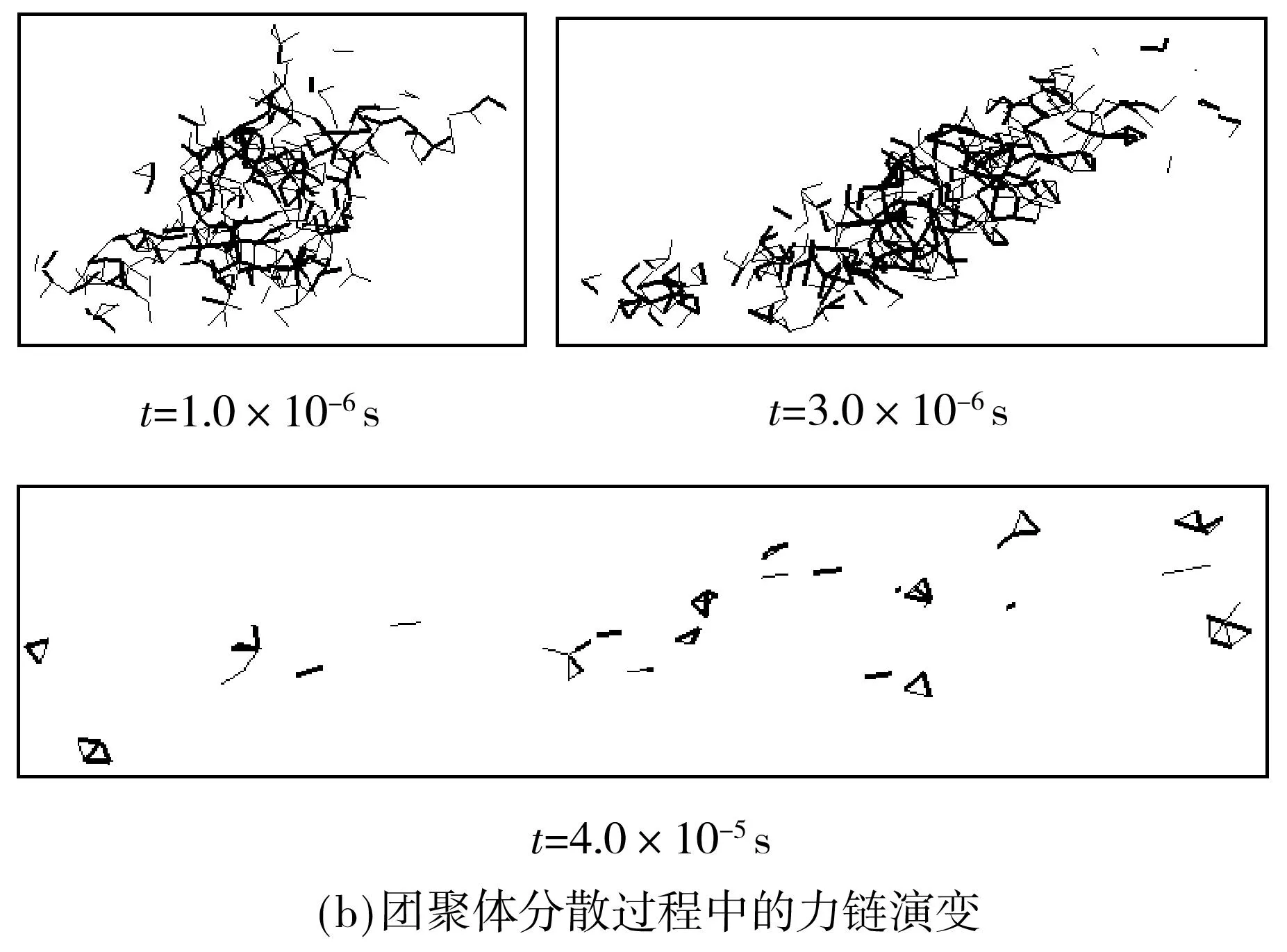
图2　流场强度为500 Pa时团聚体的分散过程及力链演变Fig.2　Evolution of dispersion and force chain network in shear flow fields at 500 Pa

由图2(a)可知，团聚体受力后先发生变形，而后再分散成碎片或者颗粒.图2(b)为相应时刻团聚体的力链结构，对比可知，复杂密集的力链网络是颗粒团聚体的内在细观结构，力链网络是颗粒传递流场作用力的路径.由图2(b)中t=1.0×10-6s时刻的情况可看出，团聚体的力链结构由强弱力链交织形成，呈无规则、复杂的网络形态，力链充分发展连接起整个颗粒体系，强力链主要分布在力链网络内部，传递较大份额的流场作用力，弱力链传递小份额的流场作用力并充分分布在力链网络中.

图2(b)中t=3.0×10-6s时刻所示为拖曳力作用下团聚体力链网络变形、破裂和重组后的形态，图中团聚体力链网络沿受力方向拉伸变形，并且破裂成一大一小的两个力链网络及其他零散的短力链.对比图2(a)中相同时刻团聚体分散形态可知，当力链网络破裂分解形成多个力链网络时，实际上就是团聚体剥蚀和破裂出单体颗粒或者尺度较小的团聚体碎片，并且碎片和颗粒的分布形态与力链网络的结构形态是一致的.

随着分散的进行，力链网络形成如图2(b)中t=4.0×10-5s时刻所示的形态，初始复杂密集的团聚体力链网络破裂、分解和重组形成若干简单、短小的力链网络，并且这些零散的力链网络中一般以强力链为主，与弱力链形成较为稳定的力链结构，在拖曳力的作用下能够变形、重组，但很少再破裂分解.颗粒间形成以强力链为主的简单力链网络结构时，颗粒间的接触关系更为紧密，碎片中的颗粒不易再被分散，最终形成零散但却较为稳定的颗粒体系.

2.2剥蚀和破碎

剥蚀和破裂是团聚体分散的两种典型方式，剥蚀指的是颗粒从团聚体表面一颗颗剥蚀出来，脱离团聚体后不再与其他颗粒发生接触，破碎指的是团聚体从内部某个接触不够紧密的位置破裂分解成尺寸较小的颗粒团簇，即团聚体碎片[14- 15].

图3(a)和3(b)所示为团聚体发生剥蚀行为前后颗粒位置的变化及对应时刻力链结构的变化.图3(a)t=4.0×10-5s时刻所示矩形框中的颗粒位于团聚体外围，与其他颗粒有接触关系，在流体拖曳力的作用下，发生剥蚀后脱离团聚体，在空间中形成单体颗粒.对比t=4.0×10-5s时刻的颗粒位置与力链结构可知，发生剥蚀的颗粒原本与其他颗粒接触形成弱力链且位于团聚体力链网络分支末端，发生剥蚀后，分支末端的弱力链消失，如图3(b)t=5.0×10-5s时刻的力链结构图矩形框内所示.因此，从团聚体细观结构角度可以认为，当团聚体力链网络外围分支末端的力链断裂消失时，即为颗粒发生剥蚀行为.

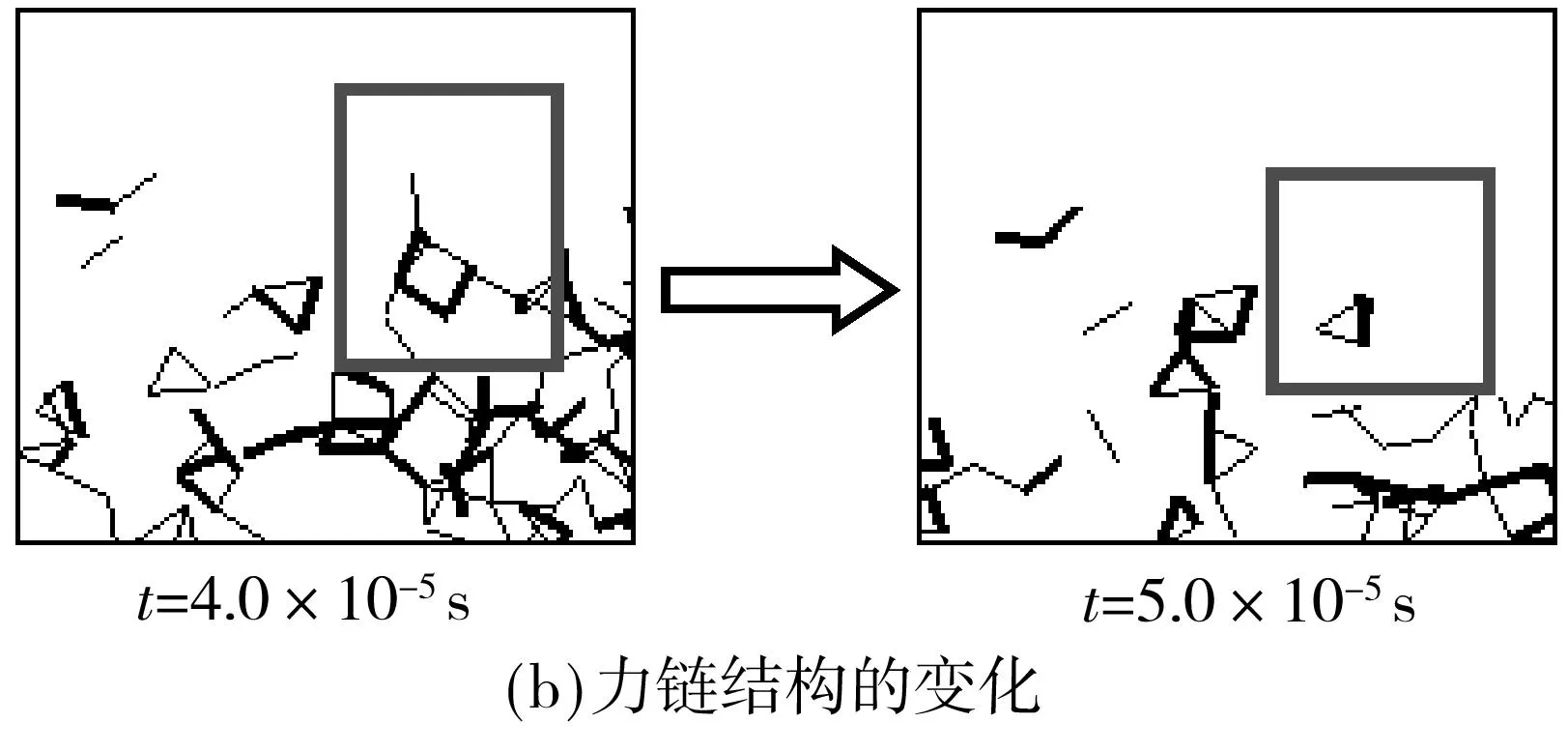
图3　团聚体的剥蚀

图4(a)和4(b)为团聚体发生破碎行为分解成尺寸较小的碎片及对应时刻团聚体力链结构的变化.如图4(a)t=1.0×10-5s时刻所示，团聚体中的颗粒呈密集分布状态，但在流体拖曳力的作用下，团聚体中接触较弱的位置(矩形框所示位置)发生了破碎行为，团聚体分解成尺寸较小的碎片.从团聚体力链网络在发生破碎前后的变化可以看出，拖曳力的作用导致团聚体力链网络内部弱力链连接处发生断裂，变形重组形成多个尺度较小的力链网络，即团聚体碎片的力链网络.因此，可以认为团聚体力链网络从内部发生整体破裂形成尺度较小的力链网络时，即发生了破碎行为.

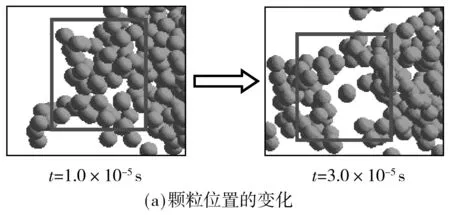
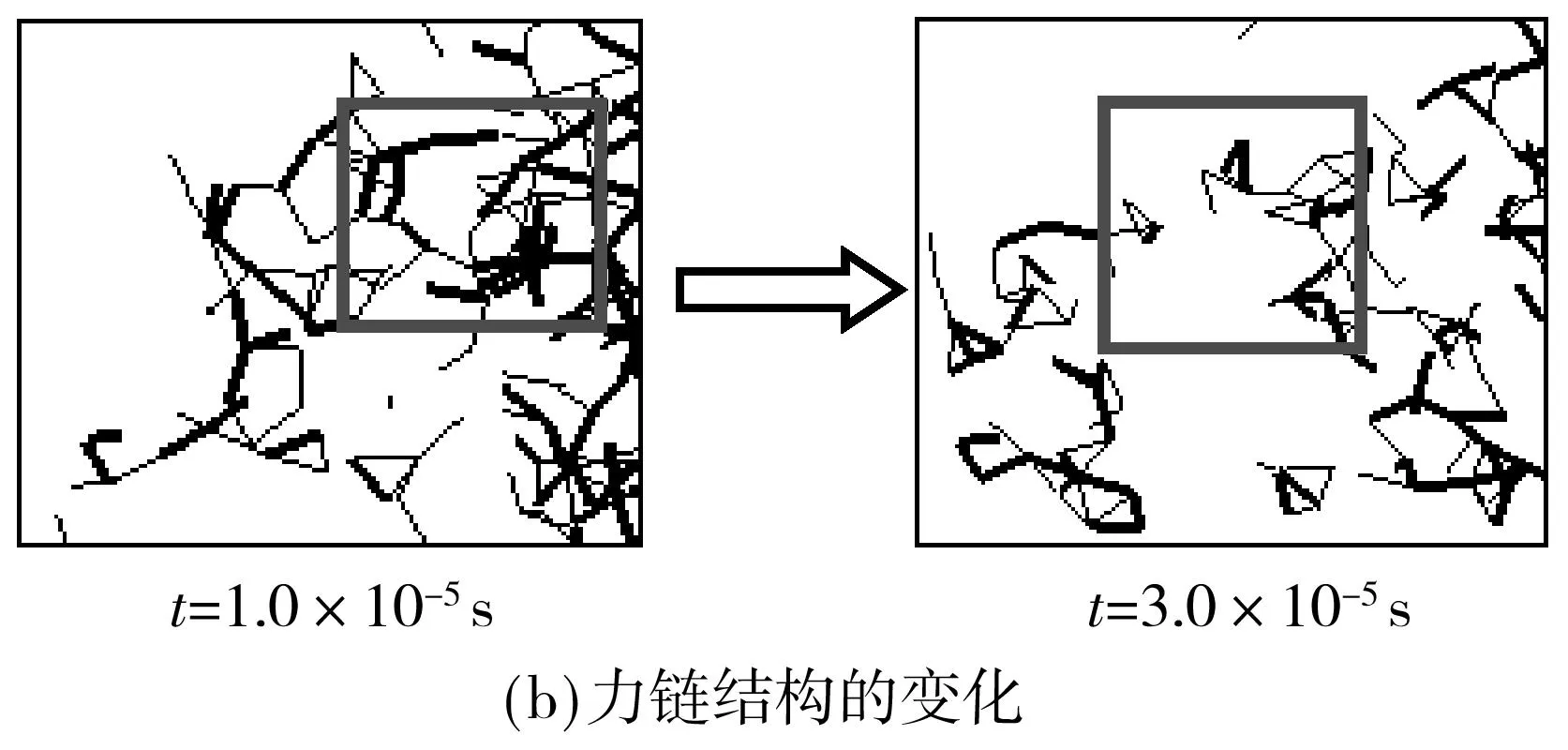
图4　团聚体的破碎

2.3流场强度对团聚体分散效果的影响

以团聚体分散过程中的碎片加权平均颗粒数来表征团聚体的分散度，定量分析流场强度对团聚体分散效果的影响，并采用分散度随时间的变化曲线来分析团聚体分散动力学过程.其中，碎片加权平均颗粒数的定义为

(13)

式中,l0为团聚体总颗粒数，nl为包含l个颗粒的碎片数.

图5为流场强度为100、500和1 000Pa时团聚体分散度随时间的变化.由图5可知：初始阶段碎片加权平均颗粒数为500，其值并未发生变化，此时团聚体仅发生变形而没有分散;而后，当团聚体变形量达到一定程度时，团聚体开始分散，分散度下降.同时，分散过程中，已分散出来的碎片或颗粒在运动过程中会重新接触，发生二次团聚行为，使得分散度短时间内增大;最后，分散度达到稳定值时，团聚体分散达到平衡状态.

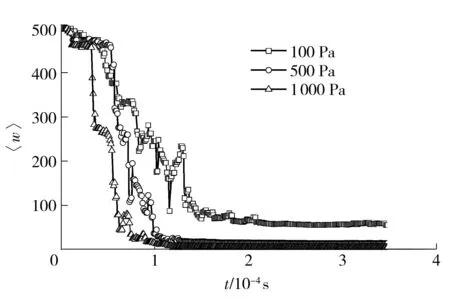
图5　不同流场强度下团聚体分散度随时间的变化

Fig.5Evolutionofdispersityofaggregationswithtimeatdifferentshearflowstress

在整个分散过程中，团聚体的分散速率呈先增大后减小的规律，分散度总体保持减小的变化趋势.分散达到平衡状态时，不同流场强度下团聚体的最终分散度(〈w〉final)变化趋势如图6所示.由图6可知，随着流场强度的增大，团聚体最终的分散度下降，但并不是以线性形式下降，其下降幅度随流场强度增大而减小，即增大流场强度对团聚体分散效果的提高是有限的，所以在聚合物填充改性加工过程中，设置合适的流场强度能够在使团聚体得到良好分散的同时降低能耗.

图6　不同流场强度下团聚体的最终分散度

Fig.6Finaldispersityofaggregationsatdifferentshearflowstress

3　结论

文中采用自主开发的三维颗粒离散元程序DEMix3D对由纳米尺度均质颗粒组成的DLA型团聚体在简单流场中的分散过程进行数值模拟，得到以下结论：

(1)强弱力链交织形成了团聚体复杂的力链网络形态，强力链主要分布在力链网络内部，传递较大份额的流场作用力，弱力链传递小份额的流场作用力并充分分布在力链网络中.在流场作用力下，力链结构发生变形、破裂和重组，形成尺度较小且更为稳定的力链结构.

(2)团聚体力链网络外围分支末端的力链断裂消失时，颗粒发生剥蚀行为脱离团聚体.团聚体力链网络从内部发生整体破裂形成尺度较小的力链网络时，团聚体发生破碎行为生成团聚体碎片.

(3)增大流场强度使团聚体最终的碎片加权平均颗粒数下降，即提高了团聚体的分散效果，但最终的分散度随流场强度的增大其下降幅度减小，说明流场强度的增大对分散效果的提高是有限的.

[1]POWELLRL,MASONSG.Dispersionbylaminarflow[J].AIChEJournal,1982,28(2):286- 293.

[2]HIGASHITANIK,IIMURAK,VAKARELSKIIU.Fundamentalsofbreakageofaggregatesinfluids[J].KONAPowderandParticleJournal,2000,18(1):26- 40.

[3]CUNDALLPA,STRACKODL.Adiscretenumericalmodelforgranularassemblies[J].Geotechnique,1979,29(1):47- 65.

[4]HOSSEINIMS,NAZOCKDASTH,DABIRB.Numericalsimulationofaggregatedispersionindifferentflowfieldsusingdiscreteelementmethod[J].JournalofAppliedPolymerScience,2010,115(6):3303- 3310.

[5]麻向军，邱忠财，陶成文．分形结构团聚体在流场中分散混合的数值模拟 [J]．华南理工大学学报(自然科学版)，2013，41(10):97- 102.

MAXiang-jun,QIUZhong-cai,TAOCheng-wen.Numericalsimulationofdispersivemixinginflowfieldofparticulateagglomerateswithfractalstructure[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition),2013,41(10):97- 102.

[6]ZHUJ,LIANGY,ZHOUY.Theeffectoftheparticleaspectratioonthepressureatthebottomofsandpiles[J].PowderTechnology,2013,234(1):37- 45.

[7]石立万，王端宜，徐驰，等．基于离散元法的沥青混合料骨架细观性能研究 [J]．华南理工大学学报(自然科学版)，2015，43(10):50- 56．

SHILi-wan,WANGDuan-yi,XUChi,etal.Investigationintomesoperformanceofasphaltmixtureskeletonbasedondiscreteelementmethod[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition),2015,43(10):50- 56.

[8]ZHOUZY,ZOURP,PINSOND,etal.Angleofreposeandstressdistributionofsandpilesformedwithellipsoidalparticles[J].GranularMatter,2014,16(5):695- 709.

[9]孙其诚，王光谦.颗粒物质力学导论 [M]．北京:科学出版社，2009:63- 70．

[10]TSUJIY,TANAKAT,ISHIDAT.Lagrangiannumericalsimulationofplugflowofcohesionlessparticlesinahorizontalpipe[J].PowderTechnology,1992,71(92):239- 250.

[11]EGGERSDORFERML,KADAUD,HERRMANNHJ,etal.Fragmentationandrestructuringofsoft-agglome-ratesundershear[J].JournalofColloidandInterfaceScience,2010,342(2):261- 268.

[12]王光谦，孙其诚．颗粒物质及其多尺度结构统计规律 [J]．工程力学，2009(A02):1- 7．

WANGGuang-qian,SUNQi-cheng.Granularmatterandthescalinglaws[J].EngineeringMechanics,2009(A02):1- 7.

[13]SUNQ,WANGG,HUK.Someopenproblemsingranularmattermechanics[J].ProgressinNaturalScience,2009,19(5):523- 529.

[14]PARKERDS,KAUFMANWJ,JENKINSD.Flocbreakupinturbulentflocculationprocesses[J].AmericanSocietyofCivilEngineers,2014,98(1):79- 99.[15]ALIGI,POTSCHKEP,LELLINGERD,etal.Establishment,morphologyandpropertiesofcarbonnanotubenetworksinpolymermelts[J].Polymer,2012,53(1):4- 28.

Foundationitems:SupportedbytheNationalProgramonKeyBasicResearchProjectofChina(2012CB619500)andtheInternationalS&TCooperationProgramofChina(2013DFG51890)

BreakupProcessandForceChainEvolutionofParticleAggregatesinFlowField

MA Xiang-junWU Zhe-hao

(TheKeyLaboratoryofPolymerProcessingEngineeringoftheMinistryofEducation∥NationalEngineeringResearchCenterofNovelEquipmentforPolymerProcessing,SouthChinaUniversityofTechnology,Guangzhou510640,Guangdong,China)

Thedispersioneffectofparticleaggregateshasadirectimpactonthecomprehensivepropertiesofcompositematerials.Inordertorevealthedispersionmechanismanddynamicdetailsofparticleaggregates,a3Ddiscreteelementprogram,Demix3D,whichinvolvesthevanderWaalsforceamongparticulates,isdevelopedtonumericallysimulatethedeformationanddispersionprocessofaggregatesinasimpleshearflowfield,andtofurtherexplorethemesostructureevolutionoftheaggregatesinthedispersionprocess.Theresultsshowthatcomplexforcechainnetworkcausedbytheinterwiningofstrongandweakforcechainsformintheaggregates.Inthisnetwork,thestrongforcechainsmainlydistributeintheinteriorandtransferthemajorityoftheforcefromtheflowfield,whiletheweakforcechainsfullydistributeinthenetworkandtransfertheminorityoftheforce.Moreover,itisfoundthatthedispersionmodeoftheparticlesisdirectlydeterminedbytheevolutionoftheforcechainnetwork,andthatthefragmentsnolongerdisperseduetotheclosecontactamongtheparticleswithstrongforcechainswhenthedispersionoftheparticlesreachesitsequilibrium.Inaddition,theeffectofflowfieldintensityonthedispersionoftheaggregatesisanalyzedaccordingtotheweightedaverageparticlenumberofthefragments.

particleaggregate;erosion;rupture;forcechain;discreteelementmethod

麻向军(1966-)，男，博士，副教授，主要从事材料成型过程的数值模拟研究.E-mail:xjma@scut.edu.cn

1000- 565X(2016)06- 0065- 05

TB115

10.3969/j.issn.1000-565X.2016.06.011

2015- 11- 27

国家重点基础研究发展计划项目(2012CB619500)；国际科技合作专项(2013DFG51890)