大坝与抗力山体联合抗滑计算方法的初步探讨

彭文明

(中国电力建设集团 成都勘测设计研究院有限公司,成都　610072)



大坝与抗力山体联合抗滑计算方法的初步探讨

彭文明

(中国电力建设集团 成都勘测设计研究院有限公司,成都610072)

摘要：与抗力山体联合作用是大坝抗滑稳定常用的措施，但由于受力复杂，通常采用有限元等方法进行安全评价。出于工程实用的需要，采用材料力学方法对大坝与下游抗力山体联合作用的受力状况进行分析，并以重力坝坝基刚体极限平衡抗滑稳定求解方法为基础，提出坝基抗滑稳定计算简易方法，并推导出相关公式。通过与有限元分析方法进行对比分析，认为材料力学方法的基本假定较为合理。结合典型算例和工程实例，进行抗滑稳定计算。结果表明：对于该工程实例，在正常工况下，不考虑下游山体的抵抗作用及考虑该作用时，坝体抗滑稳定系数分别为2.97和4.87; 在地震工况下，这2个抗滑稳定系数分别2.24和3.89; 考虑抗力山体作用后，2种工况安全系数均大幅度提高。作为一种探索复杂受力状况下坝基稳定问题的方法，其物理力学意义清晰，计算过程简便，对于解决工程实际问题具有便捷性和实用性，其求解思路也可供其它类似工程的大坝抗滑稳定计算参考。

关键词：坝基抗滑稳定；抗力山体；材料力学法； 极限平衡； 安全系数

1研究背景

抗滑稳定是混凝土水工建筑物需要重点关注的问题之一。常规的抗滑稳定计算，在重力坝、闸坝等设计规范中均有详细说明。而对于岸坡挡水坝段或取水口挡水建筑物，经常会遇到水工建筑物与下游山体紧密结合的情况(如图1所示)。事实上，利用下游抗力体协助大坝抗滑，是提高工程抗滑稳定常采用的处理措施[1-2]。

图1　取水口坝段剖面图

由于与山体联合作用，坝基受力条件复杂，评价抗力山体对大坝抗滑稳定的作用，通常采用有限元方法。出于工程实用的需要，本文尝试采用材料力学方法进行抗力山体联合作用下的力学分析，并基于刚体极限平衡原理推求抗滑稳定计算方法。

2大坝与抗力山体联合作用下的受力分析

大坝与下游山体紧密相连时，受力情况较为复杂。图2为大坝结构受力示意图，图中ΣW，ΣP，ΣM分别为大坝建基面以上竖向、水平荷载以及对建基面中心点的弯矩，来自于坝基面AB的荷载主要有扬压力U1、基岩竖向作用力N1和水平作用力F1，下游山体接触面BC的荷载主要有扬压力U2及分别与BC垂直和平行的作用力N2和F2。

图2　与抗力山体联合作用 下大坝受力示意图

当大坝体型、上下游水位、淤沙等条件确定时，ΣW，ΣP，U1，U2是已知荷载。N1，F1，N2，F2均为未知荷载，按照文献[3]的规定，可假定N1和N2为线性分布荷载；F1和F2分布情况较为复杂，但其分布不影响合力力矩，因此采用刚体极限平衡原理计算时，只需关心其合力大小即可。

3采用材料力学法简化求解

基于与抗力山体联合作用大坝的受力分析，下面尝试采用材料力学法进行简化求解。

3.1方程推导

根据力系平衡，列出图2中大坝受力平衡方程，以向下游为x正向，竖直向上为y正向，逆时针为力矩正向，由ΣFx=0，ΣFy=0，ΣMxy=0得：

ΣP-F1-(N2+U2)sinθ-F2cosθ=0 ；

(1)

ΣW-U1-N1-(N2+U2)cosθ+F2sinθ=0 ；

(2)

ΣM+MU1+MN1+MN2+MU2+MF2=0 。

(3)

当上述变量得到求解后，建基面抗滑稳定安全系数可通过式(4)求解：

(4)

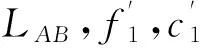
3.2基本假定

由于N1，F1，N2，F2，K为未知力，而N1和N2均假定为线性分布力，其隐含未知量有2个，所以共有未知量7个，为使式(1)至式(4)可解，本文作如下假定：

(1) 对于N2，当BC相对AB较短且为均质岩体接触面时，q21和q22相差不大，因此可假定q21=q22，于是MN2=N2(LABcosθ+LBC)/2。

(2) 对于N1，在上游水推力作用下，q11作用点远离下游山体，山体抗力作用对q11影响较小，忽略山体抗力作用影响后，按规范方法[4]求解，即

(5)

(3) 当利用下游山体作为抗力体时，其岩石质量要求较好，此时开挖面较陡(坡比一般大于1∶0.5)，大坝在水推力作用下，BC面上主要形成N2抗力，而F2相对较小，因此假定F2=0。

进行上述假定之后，未知变量减少为4个，即N1(或q12)，F1，N2(或q21,q22)，K，方程组式(1)至式(4)可解。

将式(1)至式(3)中已知量U1和U2合并到ΣP，ΣW，ΣM中，分别计为ΣP′，ΣW′，ΣM′ ，可得

(6)

对式(6)求解可得

(7)

由式(7)可求解N1，F1，N2，然后通过式(4)即可求解坝基面抗滑稳定安全系数K。

3.3基于有限元分析的论证

对于3.2节的基本假定，下面通过算题进行论证。

图3　典型例题示意图

对图3所示例题，大坝高80 m，坝体重度取24 kN/m3，上游水头75 m，下游水位低于建基面高程，基岩为Ⅲ1类岩体，允许承载力5～7 MPa。大坝体型几何参数见图3。

对例题进行有限元分析，主要获取大坝与建基面和下游抗力山体之间应力分布情况，进一步验证3.2节的假定是否合理。本例题有限元网格如图4所示，对模型进行线弹性分析，坝体弹性模量30 GPa、泊松比0.16，基岩弹性模量20 GPa、泊松比0.2。

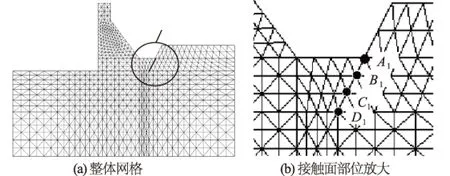
图4　有限元网格

在正常蓄水荷载作用下，进行大坝有限元分析；为便于对比，分别进行有、无抗力山体作用的计算，其坝基面竖向应力分布见图5。从图中可以看出，在抗力山体作用下，坝基竖向应力分布发生较大变化，竖向压应力沿x轴先增大后减小。坝踵及坝基中部的应力水平及变化规律，有、无山体抗力2种情况差异不大；但坝趾附近，有山体抵抗时，竖向应力比无山体时明显减小。

图5　坝基面竖向应力分布

有无山体抗力2种情况下坝踵应力分别为-0.78 MPa和-0.7 MPa，较为接近；考虑到有限元计算在角点存在应力集中现象，因此对坝踵附近节点应力进行加权平均，所得坝踵竖向应力分别为-0.85～-0.9 MPa(有山体抗力)和-0.80～-0.85 MPa(无山体抗力)，还是较为接近。由上述分析，可以初步判断3.2节第(2)条假定较为合理。

将大坝与抗力山体接触面上单元节点应力提取出来，并将应力变换为接触面法向应力和切向应力(按1∶0.5坡比转换)，如表1所示。

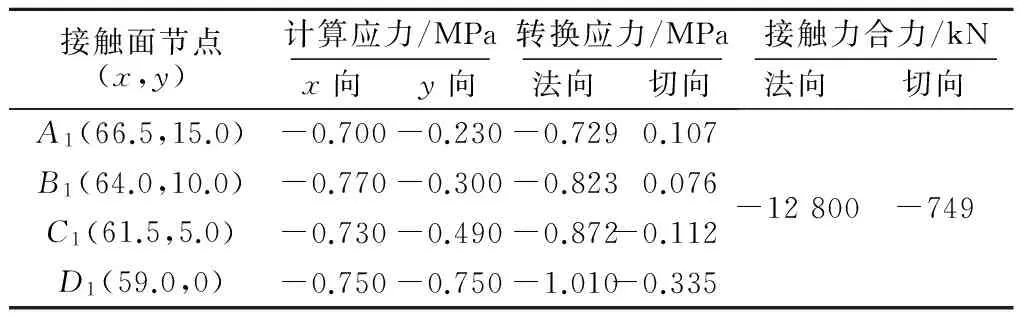
表1　接触面应力转换表Table 1　Conversion of stresses on the interface between dam and mountain

从表中可知，接触面法向应力大小总体较为接近(D1为拐点，稍微偏大，可不纳入比较)，应力范围-0.73～-0.87 MPa，变幅约16%；切向应力有正有负，合力值较小，约为法向应力合力的5.85%。因此，可以初步判断3.2节第(1)、第(3)条假定较为合理。

通过上述有限元计算分析，进一步论证3.2节的基本假定较为合理。

4例题试算

4.1典型例题

4.1.1例题基础资料

对图3所示例题进行建基面抗滑稳定试算。AB和BC面抗剪断参数均为f ′=1.0，c′=0.9 MPa。为简便起见，坝基扬压力取三角形分布，坝趾处扬压力取0，其它荷载均不计。

通过计算，可得各荷载如表2所示。

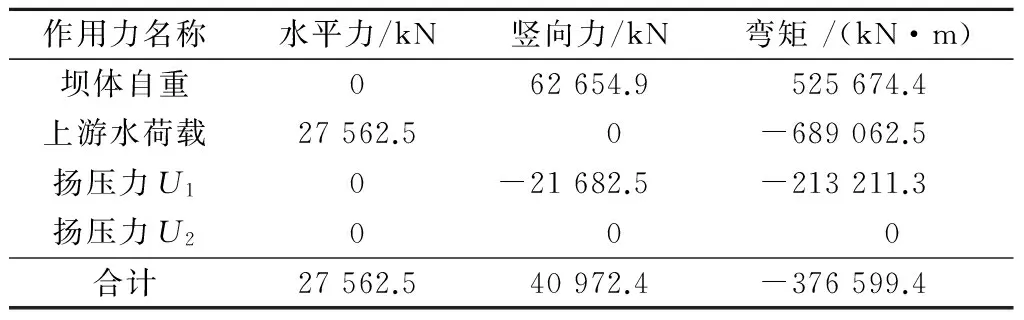
表2　例题1主要荷载Table 2　Major loads in example 1

由式(5)可得q11=-780.3 kPa(受压)。

4.1.2抗滑稳定计算

首先采用式(8)进行无山体抵抗作用的建基面抗滑稳定计算，即

(8)

考虑山体抵抗作用后，采用本文材料力学法进行建基面抗滑稳定求解，计算结果如表3所示。

表3　例题1考虑山体抵抗作用的抗滑稳定安全系数Table 3　Anti-sliding stability factor in consideration of mountain resistance in example 1

从计算结果可知，本例题大坝只有80 m高，下游抗力体接触面高15 m，在抗力山体作用下，建基面安全系数由3.41提高为15.47，山体抗力作用相当明显。

值得注意的是，本文利用了山体抗力，因此需复核山体应力是否在承载范围内。求解q21和q22可得接触面BC的正向应力，本例为1.48 MPa，远小于Ⅲ1类岩石的允许承载力5～7 MPa。

4.1.3不同F2的敏感性分析

前述假定F2=0，但事实上F2是存在的。宏观分析，F2不为0时，N1将增大、F1将减小，对抗滑稳定是有利的。结合本例3.3节中的有限元分析，F2约为N2的5.85%，下面进行F2=a·N2(a=0～10%)的敏感性分析，计算结果如表4所示。

表4　不同F2假定的敏感性分析Table 4　Sensitivity analysis in the presence of different F2 values

从表4可知，随着F2的增大K值有所提高。为安全起见，本文假定F2=0是可以接受的。

4.2工程算例

图6为某工程挡水坝段剖面图，坝高186 m，坝体重度取24 kN/m3，上游水头182 m，下游水位低于建基面高程，淤沙高度66 m，水平建基面为Ⅱ类岩石，抗力山体以Ⅲ1类岩体为主，其允许承载力5～7 MPa，下游坝趾平台高20 m。AB面抗剪断参数f ′，c′分别为1.1，1.1 MPa,BC面抗剪断参数f ′，c′分别1.0，0.9 MPa。灌浆帷幕距坝踵14.5 m，扬压力折减系数取0.35。地震加速度取0.3g。为简便，其它荷载均不计。大坝体型几何参数如图6所示。

在联考是大学入学唯一管道的年代，对她和我这种普通高中生而言，不管冷热、无论晴雨，都是适合认真念书的天气，也都该认真念书。我和她都有这种觉悟，而且为了避免升学压力太大而导致精神失常，我们也同时有了要常说冷笑话解压的觉悟。

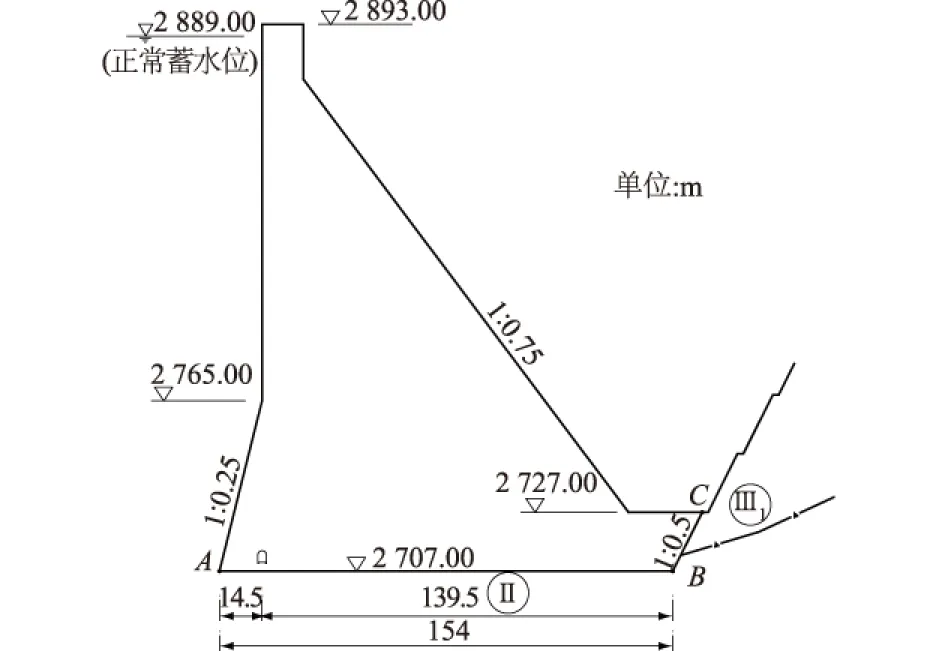
图6　工程算例剖面图

通过计算，可得各荷载如表5所示。

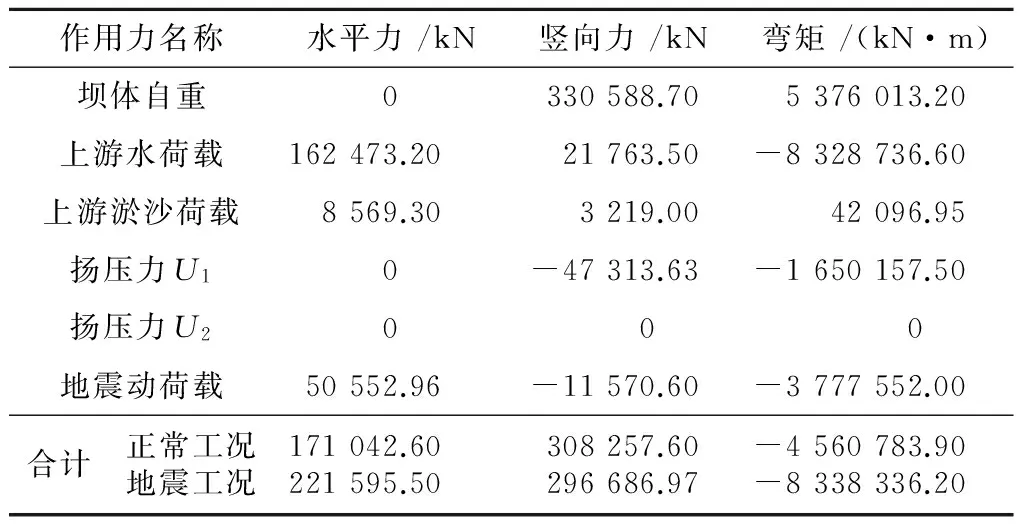
表5　工程算例主要荷载Table 5　Major loads in the engineering example

由式(5)可得q11为-1 572 kPa(正常工况)、-877 kPa(地震工况)。

本例题不考虑下游山体的抵抗作用时，采用式(8)进行建基面抗滑稳定计算，可得K正常=2.97、K地震=2.24，不满足规范[4]要求。下面考虑下游抗力山体作用进行抗滑稳定计算，计算结果如表6所示。

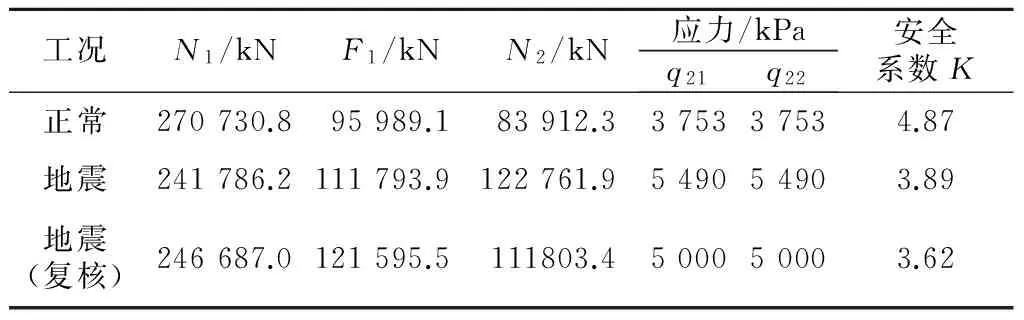
表6　工程算例计算结果Table 6　Calculation result of engineering example

从表6可知，考虑抗力山体作用后，2种工况安全系数提高均较多，能满足规范要求。但是，由于抗力山体Ⅲ1类岩石的允许承载力为5～7 MPa，而接触面BC应力q21和q22为3.75～5.49 MPa，地震工况偏高，大于允许承载力最低值。

根据潘家铮“最大值原理”[1]，滑面抗力能自行调整，以发挥最大的抗滑能力。若以允许承载力最低值进行控制，则超出抗力山体允许承载力的荷载将由其它抗滑面分摊。因此，假定BC面正向应力为5 MPa进行复核，计算结果见表6，安全系数由3.89降低到3.62。

5结语

本文采用材料力学方法对大坝与下游抗力山体联合作用的受力状况进行分析，并以重力坝坝基刚体极限平衡抗滑稳定求解方法为基础，提出大坝与抗力山体联合作用的坝基抗滑稳定计算简化方法。从方法的推导过程看，本文方法作为一种复杂受力状况的坝基稳定求解探索，其物理力学意义清晰。通过例题试算，进一步证明了抗力山体对大坝安全稳定的作用非常明显，而计算过程的方便性，也说明本文方法具有较好的工程实用价值，其求解思路还可供其它类似工况的大坝抗滑稳定计算参考。

基于该方法的边界条件，在使用过程中如下几方面值得注意：

(1) 山体自身稳定是前提。大坝与下游山体联合抗滑的工程较多，抗力体自身的性能对抗滑破坏的模式影响较大[5]。采用本文方法进行稳定计算的前提是，山体自身稳定且刚度大，能承受坝体荷载，而山体本身不产生变形破坏或失稳。

(2) 计算复判。采用本文方法获取安全系数K后，还应复核下游接触面应力是否处于山体允许承载力安全范围内。如果超出承载允许范围，则计算结果已经失真，按照“最大值原理”可取q21(q22)为山体允许承载力，再重新计算K作为最终结果。

参考文献：

[1]潘家铮.建筑物的抗滑稳定和滑坡分析[M].北京：水利出版社，1980: 211-213.

[2]潘家铮.重力坝设计[M].北京：水利电力出版社，1987: 174.

[3]祁庆和.水工建筑物(第三版)[M].北京：中国水利水电出版社，2001:60-62.

[4]SL319—2005, 混凝土重力坝设计规范[S].

[5]常晓林，王辉，周伟,等.重力坝两种滑移失稳机理及安全度评价方法[J].水利学报，2009, (10): 1189-1195.

(编辑：占学军)

收稿日期：2015-01-30; 修回日期: 2015-11-19

作者简介：彭文明(1978-)，男，江西宜春人，高级工程师，硕士，主要从事水电工程设计研究，(电话)028-87399933(电子信箱)pwm02@163.com。

doi:10.11988/ckyyb.20150101

中图分类号：TV315

文献标志码：A

文章编号：1001-5485(2016)04-0115-05

A Simplified Solution to the Slide-resistant Stability of Dam Jointedwith Mountain Rock: Based on Material Mechanics

PENG Wen-ming

(Power China Chengdu Engineering Corporation Limited, Chengdu610072, China)

Abstract:To joint a dam with resistant mountain rock is a common measure against sliding. Due to complicated forces in this case, finite element method is usually adopted in the safety evaluation. In this research, we applied mechanics of material to analyse the forces between the dam and the downstream mountain rock mass. Moreover, we put forward a simplified method of calculating the slide-resistant stability of dam foundation and deduced the formula based on rigid-body limit equilibrium solution for gravity dam foundation. By comparing it with finite element method, we conclude that the basic assumption of the present method based on material mechanics is reasonable. Furthermore we applied this method to the calculation of a typical calculation example and an engineering example. Results show that as for the engineering example, the anti-sliding safety factor is 4.87 and 2.97 respectively in the presence and in the absence of mountain rock resistance under normal working condition, and 3.89 and 2.24 under seismic condition. The safety factors in both conditions are greatly improved in the presence of mountain rock resistance. As a preliminary exploration on dam foundation with complex forces, the method has clear physical and mechanical meaning, and convenient calculation process.

Key words:slide-resistant stability of dam foundation; resistant rock; mechanics of materials; limit equilibrium; safety factor

2016,33(04):115-119