边坡稳定性分析中传递系数法显式解和隐式解安全系数的对应关系探讨

邱永平 刘菀茹 张东卿 罗一农

(中铁二院工程集团有限责任公司， 成都 610031)

边坡稳定型分析是一个研究历史比较悠久的课题，稳定性计算也有相当多的成熟方法，如瑞典圆弧法(Fellenius法)、简化Bishop法、简化Janbu法、美国陆军工程师团法、罗厄法(Lowe-Karafiath)、Sarma(I)法、Morgenstern-Price法、Spencer法、不平衡推力法(传递系数法)等。其中，传递系数法在我国工程建设中应用普遍。传递系数法按安全系数作用的不同可分为增大下滑力法和滑面强度折减法，增大下滑力法可得出稳定系数的解析解，也称为显示解法。强度折减法需经迭代计算才能得出稳定系数，也称为隐式解法。

不同行业现行规范中边坡稳定的推荐求解方法如表1所示，从表中可以看出各行业推荐采用的方法并不统一。在计算机应用尚未普遍应用时，显式解法由于求解比较方便，在国内应用广泛，在安全系数如何取值上也得到了大量经验，因此各行业规范普遍采用显式解法。

由于显式解法采用了增大下滑力的方式，而其它稳定计算方法都采用滑面强度折减的方式，计算原理的差异使显式解法常常受到质疑，各个行业也逐渐开始采用隐式解法。从而在稳定计算时，面临显式解法和隐式解法的安全系数取值如何匹配，才能使两者边坡稳定性评价结果相同的问题。同时随着数值分析强度折减法在边坡稳定性分析中的广泛应用，大型工程滑坡要求同时采用传递系数显式解法和数值分析强度折减法进行计算分析，同样面临两种算法安全系数取值匹配的问题。长期以来，业内同行为研究两者的匹配关系做了大量工作，但均未取得实质性成果。本文对此展开研究，以供同行参考。

表1 各行业现行规范求解方法一览表

部分规范的安全系数取值如表2所示。

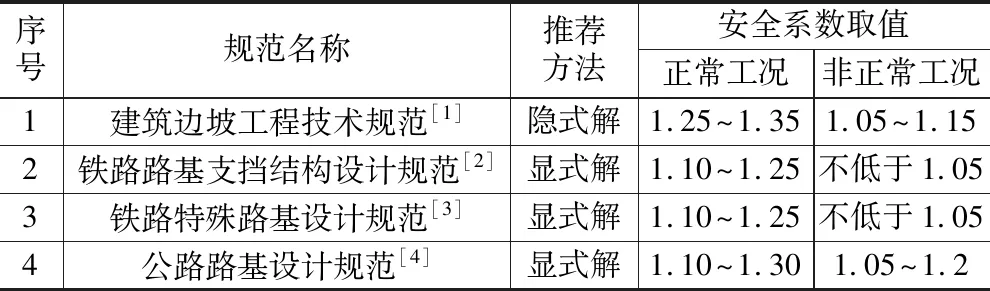
表2 各规范的安全系数取值表

1 传递系数法的计算表达式

显式解法和隐式解法的推力表达式如式(1)和式(2)所示， 显式解法把安全系数放在下滑力处，使下滑力增加Kx倍；隐式解是把安全系数放在抗滑力处，使抗滑力减小Ky倍。

显式解(增大下滑力法)：

Ti=KxWisinαi+ψTi-1-(Wicosαitanφi+cili)

(1)

其中，传递系数ψ=cos(αi-1-αi)-sin(αi-1-αi)tanφi

隐式解(强度折减法)：

(2)

其中，传递系数ψ=cos(αi-1-αi)-sin(αi-1-α1)tanφi/K

式中：Ti——第i个条块末端的滑坡推力(kN)；

Kx、Ky——安全系数；

Wi——第i个条块滑体的重力(kN)；

αi——第i个条块所在滑动面的倾角(°)；

αi-1——第i-1个条块所在滑动面的倾角(°)；

φi——第i个条块所在滑动面上的内摩擦角(°)；

ci——第i个条块所在滑动面上的单位黏聚力(kPa)；

li——第i个条块所在滑动面上的长度(m)。

2 传递系数法计算理论分析

本文对直线形和折线形滑面分别进行分析，以找出显式解和隐式解之间的关系。

2.1 直线型滑面

(1)显式解与隐式解出口推力比值

当滑面为直线时，αi-1-αi=0，条块的倾角差均为0，滑体可视为整体简化计算。

传递系数ψ=cos(αi-1-αi)-sin(αi-1-αi)tanψi=1，由于不存在分块，故Ti-1=0，即ψTi-1=0。

则显式解与隐式解出口推力比值式(1)/式(2)可简化得：

(3)

当安全系数取同一个K时，显式解与隐式解出口推力比值等于K。

(2)显式解与隐式解安全系数的对应关系

显示解法和隐式解法相匹配的前提前件是使两种方法求解的出口推力相等，即：

(4)

整理方程，得

(5)

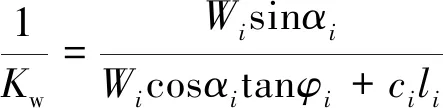
(6)

(7)

(8)

式中：Kx——显式解安全系数;

Ky——隐式解安全系数;

Kw——滑体当前稳定系数，Kw=(Ntanφi+cili)/T。

式(6)、式(7)和式(8)即为显式解和隐式解的对应关系，3个公式等效。由式(6)可知，Kx、Ky的关系与边坡当前的稳定系数Kw有关，不同稳定系数的边坡其对应关系均不相同。而之前的研究基本上都忽略了这个因素，只通过单纯研究Kx、Ky之间的联系，以期得到单一直接的对应关系，故而未取得实质性进展。计算Kx、Ky、Kw对应关系，如表3所示。

表3 Kx、Ky、Kw对应关系表

注：设计中安全系数取值需大于稳定系数，才可以算出剩余下滑力，故表中空格不列数据

表中第一行为稳定系数，第一列为显式解安全系数，中部为某个稳定系数下，与显式解安全系数对应的隐式解安全系数，这些均为设计中常见的系数。通过边坡稳定分析软件计算表中对应显式解与隐式解安全系数的滑坡出口推力，结果表明两者计算出的出口推力结果完全相等。这说明直线滑面时，表3中的对应关系是正确的，同时也验证了式(6)～式(8)的正确性。

在实际设计中，通常假定滑坡稳定系数Kw=1.0，通过反算得到滑面c、φ值，然后指定安全系数计算滑坡推力，此时，可采用表4中隐式解与显示解安全系数的对应数据。若稳定系数不等于1.0，则建议采用表3进行内插或采用式(6)～式(8)进行计算来求得对应的隐式解与显式解安全系数。

表4 Kx、Ky对应关系表(稳定系数等于1.0时)

(3) 滑体中部显式解与隐式解的推力关系

对于直线型滑面，取对应的显式解与隐式解安全系数，使两者的出口推力相等。当c=0时，滑体中部的隐式解推力仍等于显式解，推力曲线完全重合。当c>0时，滑体中部的隐式解推力小于显式解推力，隐式解推力曲线低于显式解推力曲线，如图1所示。

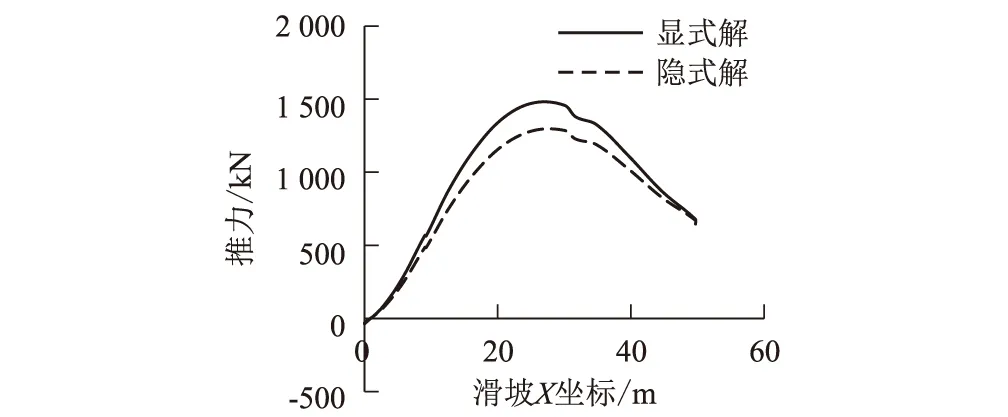
图1 某边坡显式解和隐式解的推力曲线图

2.2 折线型滑面

当滑面为折线型时，由于需考虑滑块间力的传递，得出简明直观的显式解和隐式解安全系数的对应关系表达式难度较大，本文尚未解决这一问题。但通过大量验算，总结规律如下：

(1)对于折线型滑面，对应关系式以下式表达：

(9)

式中：β——折减系数，取值0.97～1.0。

折减系数取值与滑面形态、滑坡当前稳定性、安全系数取值等因素有关。通常当滑面弧度越大、滑坡当前稳定系数越大、安全系数取值越大时，采用的折减系数越小。

(2) 当显式解与隐式解安全系数取值相同时，显式解与隐式解出口推力的关系如下：

①当安全系数为1时，显式解和隐式解的表达式完全相同，两者计算得出的滑体各点推力均相等。

②当安全系数小于1时，显式解的推力计算值小于隐式解计算值，两者比值大于安全系数。但实际设计时安全系数不会小于1，因此此解无实际意义。

③当安全系数大于1时，显式解的推力计算值大于隐式解，两者推力比值一般小于安全系数。滑面越直，显式解与隐式解的出口推力比值越大，越接近指定的安全系数，当滑面为直线时，两者比值等于指定安全系数。

(3)当显式解与隐式解取不同的安全系数，使两者的出口推力相等时，滑体中部的隐式解推力小于显式解推力。

3 结束语

本文通过理论分析和大量计算，对边坡稳定性分析中传递系数法显式解和稳式解安全系数对应关系进行了研究，总结出了一些规律，对边坡设计有一定指导意义，建议规范转轨或实际设计时可采纳以下意见：

(1)对于直线型滑面，精确的安全系数对应关系值。应参考表3或式(6)～式(8)，并结合滑体当前稳定系数选取或计算。

(2)对于折线型滑面，隐式解安全系数取值可在式(7)基础上进行折减，即按式(9)计算。折减系数取值0.97～1.0，折减幅度与滑面形态、滑坡当前稳定性、滑面抗剪强度取值、安全系数取值等因素有关。通常滑面弧度、滑坡当前稳定系数、安全系数取值越大时需采用的折减幅度越大。

(3)强度折减法数值分析时，可采用计算出的隐式解安全系数进行分析。

(4)显式解的安全系数取值为1.05～1.25时，其隐式解的建议取值为：直线型滑面取1.05～1.35；折线形滑面取1.05～1.35，并进行折减，折减系数0.97～1.0，中间值可按式(9)计算。