三轴固结排水试验中偏应力计算取值的探讨

徐志华，张国栋，孙大伟，孙钱程

(1.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌　443002；2.三峡大学 a.湖北长江三峡滑坡国家野外科学观测研究站; b.湖北省地质灾害防治工程技术研究中心；c.土木与建筑学院，湖北 宜昌　443002)



三轴固结排水试验中偏应力计算取值的探讨

徐志华1，2a,2b,2c，张国栋1，2a,2b,2c，孙大伟2c，孙钱程2c

(1.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌443002；2.三峡大学 a.湖北长江三峡滑坡国家野外科学观测研究站; b.湖北省地质灾害防治工程技术研究中心；c.土木与建筑学院，湖北 宜昌443002)

摘要：在三轴固结排水试验中，偏应力大小的求解过程是基于试样始终是等体积圆柱体的假定来进行推导的，该假定认为在整个试验过程中，试样任意横截面的面积相等。但是在试验过程中，由于端部效应的存在，使得试样在轴向加载的过程中逐渐变成了鼓形，这与偏应力的计算假定不符。为了计算三轴试验中鼓形试样受偏应力的大小，进行了一系列固结排水三轴试验，并根据试样的实际变形情况对试样所受的偏应力进行了重新推导。结果表明：按照实际变形情况推导出的偏应力计算公式与规范采用公式不同，根据推导公式计算的偏应力值在一个范围内变化，其最小值较规范值小，最大值较规范值大；通过计算坝体沉降量从坝体安全的角度给出了粗粒土三轴固结排水试验强度计算时偏应力的推荐值。

关键词：三轴试验；固结排水；等效圆台；粗粒土；偏应力

1研究背景

粗粒料通常是指块石、碎石、石屑、石粉等粗颗粒组成的无粘性混合料以及粘性土中含有大量粗颗粒的混合土。粗粒土因其抗剪强度高、压实性能好、填筑密度大、沉陷变形小等优良的工程特性，已在高速公路及铁路路基、高层建筑物地基、大型水利水电工程、海港护岸抛石工程中得到了广泛应用。

水布垭大坝作为世界上已建成的最高混凝土面板堆石坝， 2004 年，多家单位对其沉降变形值进行计算预测，最大预测值为1.31～1.92 m, 而蓄水1 a后实测沉降值达到了2.44 m[1]。变形稳定是坝体安全稳定的一个重要方面，水布垭大坝沉降预测工作没达到理想效果，其原因很多，其中偏应力计算的取值是影响坝体计算沉降结果的一个重要因素。

《土工试验规程》[2]在偏应力的计算过程中假定试样在试验过程中为体积等效的圆柱体，试样侧向受力均匀，且任意位置处的横截面面积大小相等。《高等土力学》等[3-4]教材及大量关于岩土材料力学特性的研究文献[5-9]中偏应力值均是在《土工试验规程》的假定下计算得出的。

本文的研究是基于大量的试验完成的，由于试验过程中试样的端部存在约束，不能侧向自由变形，与理想状态相差较大，其受力状态与规范中等截面圆柱体的假定不符。因此，本文根据试验的实际情况对偏应力的计算进行了重新推导，并以现有研究成果为基础进行了坝体的沉降计算，基于推导公式计算的坝体沉降更接近实际沉降值。

2规程偏应力计算表达式

《土工试验规程》[2]假定固结排水试验过程中的试样为等体积的圆柱体，并假设圆柱体任意点处立方体微元上的垂直向应力σ1为最大主应力；微元水平向应力σ3为小主应力，二者差值(σ1-σ3)为试样中的偏应力q，如图1所示。

图1　规程中的等效圆柱试样及微元体受力状态

规程假设试样中应力均匀分布，偏应力q的计算公式见式(1)至式(3)：

(1)

(2)

(3)

图2　三轴固结排水试验后的试样

3偏应力公式的推导

3.1等体积圆台法的提出

本文对水布垭大坝堆石料进行了围压0.6，1.0，1.6，2.15 MPa的三轴固结排水试验，试验过程严格按照《土工试验规程》SL237—1999进行。试验发现随着轴变εa的增加，试样逐渐从最初的圆柱形鼓胀为鼓形，见图2。由于试样外壁存在一定角度的倾斜，因此,围压σ3将在试样倾斜面上产生轴向的分力。

规程假设大主应力σ1为均布应力，但是实际上不同位置横截面上的大主应力σ1值是不相等的。因此，将鼓形试样简化为2个体积大小相等、方向相对的圆台，如图3所示。按等效体积法对偏应力的计算公式进行了重新推导。

图3　圆台试样尺寸及脱离体的受力状态

3.2等体积圆台法的偏应力推导

按照剪切过程中体积等效的原则，选取图3中底面积为Aa、高为ha的圆台为脱离体进行研究，上圆半径r=D(1-ε)/2，ε为固结率，D为固结前试样直径，母线长为la，侧面积为Sa。假设试验过程中试样等高度处横截面上的大主应力σ1处处相等。由几何关系可求得：

(4)

(5)

试验固结过程完成后，圆台脱离体半径为r的上圆面及面积为Sa的倾斜面上存在均匀分布的水压力(即围压σ3)。

作用在圆台试样倾斜面上的水压力在轴向产生的分力为σ3sinθ×Sa, 试样的自重相对于所受外力来说比较小，可以忽略。

圆台试样脱离体受到的力有：钢活塞施加的轴向力、围压σ3作用在试样顶面的力、围压σ3作用在圆台试样侧面上的力以及脱离体底面上的作用力。由垂直方向上力的平衡可得

(6)

式中：σ1l为作用在圆台底面Aa上的轴应力;Aa为圆台脱离体的底面积；CR×10为由钢活塞施加并由轴力传感器量测的轴力；r为圆台脱离体上圆半径；Sa为侧面积；σ3为围压。

在式(6)两端都除以Aa，有

(7)

由图3可知Aa=πr2+Sasinθ。

式(7)简化为

(8)

为了计算《土工试验规程》中的偏应力(σ1-σ3)，需要求得三轴试样中的水平向应力σ3。为此，取圆台脱离体中的微单元为研究对象。如图4(a)中O′OIBEJ所示，微弧面IBEJ面积为ds。微单元几何特性如图4(b)、4(c)所示，DAOO＇面和JIOO＇面之间的夹角为α；IBEJ面和中心轴OO′之间夹角为θ；围压σ3作用在IBEJ面上的合力为dF；dFx为dF′在垂直ACFD面上的分力。

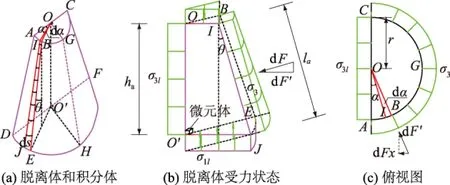
图4　半圆台脱离体受力状态

由图4中几何关系，可以得到如下关系式：

(9)

(10)

(11)

式中dF′为dF在水平方向上的分力。

可求得：

(12)

(13)

式中SACFD为梯形ACFD的面积。由于大小固定的围压σ3l作用在梯形ACFD的另一侧，由水平方向的力的平衡方程，得

(14)

因此有

(15)

式中σ3l为圆台脱离体水平方向上的小主应力。

最后，如图4(b)所示，选取圆台中心轴上的微元体，微元体轴向的大主应力为σ1l，水平向的小主应力为σ3l，微元体表面无偏应力，为简单受力状态。根据弹性力学公式，微元体内的偏应力q等于轴向大主应力σ1l减去小主应力σ3l，即偏应力计算公式为

q=σ1l-σ3l=CR/Aa×10=σ1-σ3。

(16)

式中：σ1为规程中定义的大主应力；σ3为围压。

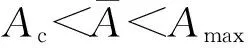
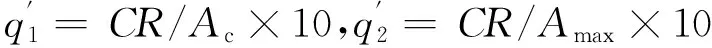
(17)

式中:Ac为试样固结后截面积(cm2)；Amax为等效圆台的下底面积(cm2)。

3.3偏应力的计算取值的确定

《土工试验规程》规定以(σ1-σ3)或(σ1/σ3)的峰点值作为破坏点，如(σ1-σ3)和(σ1/σ3)均无峰值，应以应力路径的密集点或按一定轴向应变(一般可取ε=15%, 经过论证也可根据工程情况选取破坏应变)相应的(σ1-σ3)或(σ1/σ3)作为破坏强度值。

表1　不同标准的E-B本构模型参数Table 1　E-B constitutive model parameters of different standards

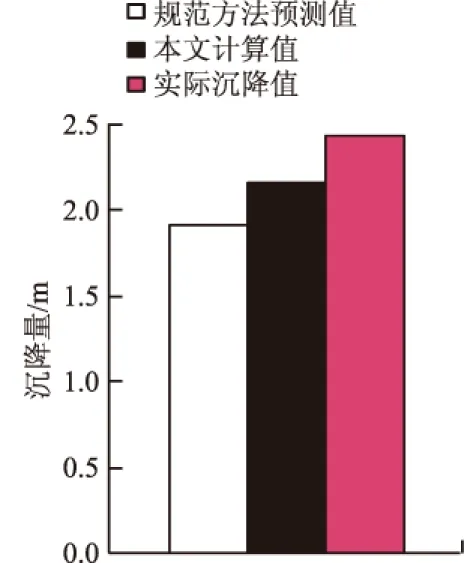
图5　计算沉降量对比

4结论

本文进行了一系列固结排水三轴试验，根据试样的实际变形情况对试样所受的偏应力进行了重新推导，并且通过实例计算，对偏应力计算取值的问题进行了探讨，获得以下结论：

(1) 在不同围压下的固结排水三轴剪切试验中，随着压力的增大，试样逐渐变成鼓形，不同位置的横截面面积不相等，围压将在试样的倾斜面上产生垂直方向的应力分量。

(4) 为大坝等构筑物填料的三轴固结排水试验的强度取值提供理论支撑，对大坝的沉降预测等以堆石料强度为基础的工程计算取值提供参考。

参考文献：

[1]《水布垭面板堆石坝前期关键技术研究》编写委员会. 水布垭面板堆石坝前期关键技术研究[M]. 北京:中国水利水电出版社,2005.

[2]SL237—1999,土工试验规程[S].

[3]谢定义,姚仰平,党发宁.高等土力学[M]. 北京:高等教育出版社,2008:130-131.

[4]陈仲颐, 周景星, 王洪瑾. 土力学[M]. 北京: 清华大学出版社,2011:119-120.

[5]刘萌成,高玉峰,刘汉龙,等.堆石料变形与强度特性的大型三轴试验研究[J].岩石力学与工程学报,2003，22(7):1104-1111.

[6]刘希亮, 刘少峰, 秦本东. 纤维混凝土三轴抗压强度及破坏特征的试验研究[J]. 河南理工大学学报, 2013, 32(2): 225-229.

[7]CAI Zheng-Yin. The Deformation Behavior of Sand[M]. Zhengzhou: Yellow River Conservancy Press, 2004: 140-164.

[8]常在, 杨军, 程晓辉. 砂土强度和剪胀性的颗粒力学分析[J]. 工程力学,2003, 22(7): 1104-1111.

[9]肖化文. 邓肯-张E-B模型参数对高面板坝应力变形的影响[J]. 长江科学院院报,2004, 21(6):41-44.

[10]孙大伟. 深覆盖层上高面板坝应力变形性状研究[D]. 南京:南京水利科学研究院,2006.

(编辑：曾小汉)

收稿日期：2015-01-07；修回日期：2015-02-02

基金项目：国家自然科学基金项目(51179097)；湖北省自然科学基金项目(2012FFA040)

作者简介：徐志华(1987-)，男，山东潍坊人，博士研究生，主要从事岩土体力学特性试验、数值模拟及本构模型研究，(电话)15072507697(电子信箱)zhihuabest@163.com。

doi:10.11988/ckyyb.20150016

中图分类号：TV41

文献标志码：A

文章编号：1001-5485(2016)04-0057-04

Discussion of Deviatoric Stress Calculation inTriaxial Consolidation Drained Test

XU Zhi-hua1,2,3,4, ZHANG Guo-dong1,2,3,4, SUN Da-wei4, SUN Qian-cheng4

(1.Collaborative Innovation Center for Geo-hazards and Eco-environment in Three Gorges Area, Hubei Province,Yichang443002,China; 2.National Field Observation and Research Station of Landsides in Three Gorges of Yangtze River, Yichang443002, China; 3. Hubei Engineering Research Center of Geological Hazards Prevention, Yichang443002, China; 4. College of Civil Engineering & Architecture, China Three Gorges University,Yichang443002，China)

Abstract:The deviatoric stress calculating process of triaxial consolidation test is based on the assumption that the sample always keeps a cylinder shape with equivalent volume and the cross sectional area of the sample is equal at any location during the test. But in actual test the sample is drum shape in the test process due to end effect, which is inconsistent with the assumption. We deduce the deviatoric stress calculation formula according to the actual situation of sample deformation in consolidated drained triaxial test. Results show that different with that in specification, the value calculated from deduced deviatoric stress formula according to the actual deformation changes in a scope, with the minimum value lower and maximum value higher than standard value. By calculating dam subsidence, we also give the recommended value of deviatoric stress in coarse-grained soil’s triaxial consolidated drained test.

Key words:triaxial test; consolidated drained; equivalent circular truncated cone; coarse-grained soil; deviatoric stress

2016,33(04):57-60