基于电性拓扑状态指数的二元液体混合物自燃温度的预测

何　凡，蒋军成，潘　勇，倪　磊



基于电性拓扑状态指数的二元液体混合物自燃温度的预测

何凡，蒋军成，潘勇，倪磊

（南京工业大学安全科学与工程学院，江苏省危险化学品本质安全与控制技术重点实验室，江苏 南京 210009）

摘要：利用AITTA551自燃温度测试仪，测得不同组分和配比下的28组168个二元可燃混合液体自燃温度（AIT）；基于电性拓扑状态指数（ETSI）理论，计算获得不同原子类型所对应的混合 ETSI值；采用添加指数递减惯性权重的改进粒子群算法（MPSO）优化支持向量机（SVM）的超平面参数，建立根据原子类型混合ETSI值来预测混合物自燃温度的MPSO-SVM模型。结果表明，基于电性拓扑状态指数能够有效预测二元液体混合物自燃温度，MPSO-SVM模型的复相关系数R2为0.991，平均绝对误差AAE为3.962 K。MPSO-SVM模型的泛化性能和预测精度明显优于多元线性回归（MLR）、网格搜索法（GSM-SVM）、遗传算法（GA-SVM）、标准粒子群算法（PSO-SVM）模型。本研究为工程上提供了一种预测二元混合物自燃温度的有效途径。

关键词：电性拓扑状态指数；二元混合物；算法；自燃温度；预测

引 言

自燃温度是指可燃物质在空气中无需任何外在火源就能够自行燃烧的最低温度[1]。可燃物质的自燃温度不仅是表征物质危险性的重要参数，也是量化风险评估的必要参数。在实际生产过程中，可燃混合有机物被各个领域广泛使用，由于环境温度或反应时高温的存在而引起可燃物质自燃的事故时有发生[2]。因此，在危险化学品生产、使用、储运等过程中，必须要把自燃温度指标考虑在内。

国内外自燃温度的相关研究还局限于纯物质或气态混合物，对混合液体自燃温度研究还相当滞后。关于纯物质方面，Pan等[3-4]利用多元线性回归（MLR）、人工神经网络（ANN）以及支持向量机（SVM）等方法对纯有机物的自燃温度进行预测。Tsai等[5]选取电性拓扑状态指数平均数、芳香比率、旋转联接分数、原子中心分段数作为分子描述符，建立自燃温度的预测模型。Bagheri等[6]利用粒子群算法筛选描述符，提出含硫有机物的自燃温度预测模型。气态混合物方面，Kong等[7]利用体积为1 L的自燃点爆炸装置对不同当量比的天然气组分混合物的自燃温度进行了测定。Rota等[8]建立预测工业混合气体（NH3/H2/CH4）自燃温度的动力学模型。Norman 等[9]研究了装有丙烷和空气混合物的球形封闭容器内的自燃温度随初始压力的变化规律。van den Schoor等[10]通过一个完全搅拌反应器模型对NH3/CH4/Air混合物的自燃温度进行了研究。

混合物自燃温度虽然可通过自燃温度测试仪进行测定，但常会遇到实验设备昂贵、测定影响因素多和过程耗时耗力的问题，导致无法在实践中大规模推广运用。因此，有必要开展混合物自燃温度的实验及理论预测研究，以期建立简单可靠的混合自燃温度预测模型。本文通过实验获取大量可靠的二元可燃混合液体自燃温度数据，并基于电性拓扑状态指数（ETSI）理论和改进的粒子群优化（MPSO）算法建立了二元混合物自燃温度的MPSO-SVM理论预测模型，能够快速有效地预测二元混合物自燃温度，给工业生产安全提供必要的混合物自燃温度物性数据支撑。

1　实验数据获取

1.1 实验仪器

本实验使用的仪器为AITTA 551自燃温度测试仪，由美国爱迪塞恩有限公司设计制造，按照ASTM E659-78标准对试液体的自燃温度进行测试。如图1所示，它包括高温加热炉、电脑软件控制以及测量单元，加热炉内温度分布均衡，烧瓶通过炉内的热风循环进行加热，3个与瓶壁接触的热电偶实时监测烧瓶的温度变化，另一个热电偶测定烧瓶内部温度；计算机系统控制仪器对热电偶和火焰检测器的数据进行采集，并自动评价测试结果。

图1　AITTA 551自燃温度测试仪内部结构Fig.1 Internal structure chart of AITTA 551 auto-ignition temperature tester

1.2 实验原理与步骤

以常见的烷、醇、醚、酮、酸、酯、苯系物等可燃有机物为实验对象，依据有机溶剂互溶表，筛选出多组完全互溶的物质，配制不同组分及浓度的二元可燃混合物。

将自燃温度实验测定步骤归纳如下。

查询纯物质的自燃温度，对不同配比的混合液体自燃温度进行预估；设置炉温初始值低于预估值30 K，炉内的热风循环将烧瓶加热到设定值，过程持续30 min以上来保持温度稳定；移取100 μl混合溶液加入 500 ml烧瓶中，检测是否发生自燃，如10 min内观察镜中出现火焰并伴随轻微爆鸣声或烧瓶内的温度瞬间升高，即可认为发生自燃；采用逼近法不断调节烧瓶的温度，步长由30 K逐渐降低到3 K，并不断重复测试过程直到测得自燃温度为止；每组实验结束后使用热风枪吹扫烧瓶，将残余样品清除，以减少实验误差。

1 . 3 实验结果与分析

通过实验测得 2 8组二元互溶混合液体在不同配比下的混合自燃温度共1 6 8个数据点。为了进一步检验实验数据的准确度，利用纯物质自燃温度的实验值同D I P P R[11]以及I C S C s[12]两大权威数据库值进行验证对比，结果见表1 。

表1　纯物质自燃温度实验值与DIPPR/ICSCs数据对比Table 1 Comparison between experimental and DIPPR/ICSCs database values of AIT for pure substances

由表1可知，纯物质自燃温度实验值与DIPPR 和 ICSCs数据库值的平均绝对误差 AAE分别为24.95、26.00 K，根据ASTM E659-78的测试标准，自燃温度实验绝对误差允许在30 K的范围内，所以可以认为整体的实验数据真实有效[13]。

2　预测理论与方法

2.1 ETSI理论

2.1.1 ETSI理论简介 电性拓扑状态指数（electrotopological state indices，ETSI）是Kier等[14]提出的一种基于分子中各个原子的原子级拓扑指数。由于ETSI既可以表现原子电子性质和拓扑性质，又能够表现该原子所受分子环境影响，已经广泛应用于物质的理化性质预测研究[15]。

2.1.2 混合ETSI值计算 表2为二元混合物中18种可燃有机物所包含的9种原子类型、ETSI符号及其固有状态值。

根据前人的研究成果[15]，将混合ETSI值的具体计算步骤总结如下。

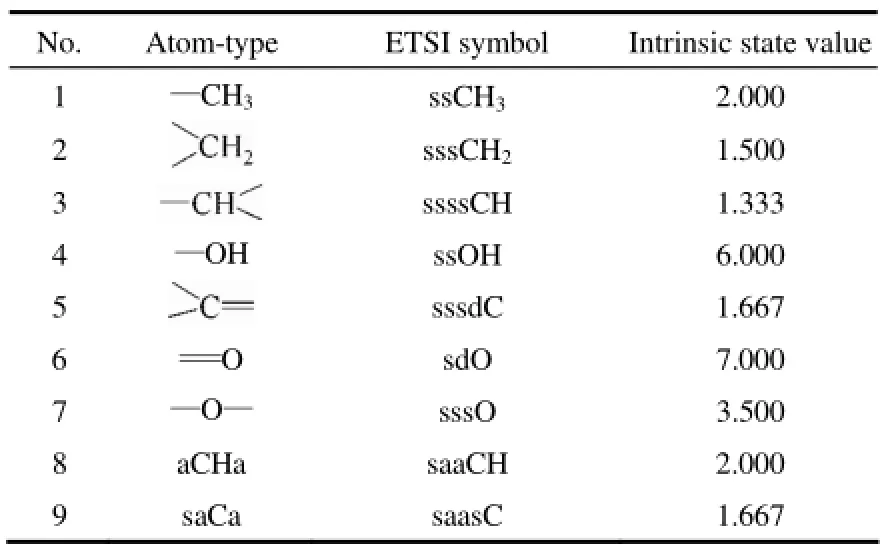
表3　9种原子类型、ETSI符号及其固有状态值Table 2 9 kinds of atomic types, ETSI symbols and intrinsic state values

(1) 计算分子中每一个非氢骨架原子所对应的固有状态值Ii

式中，N为非氢原子价电子的主量子数；δ、δv分别为分子骨架中原子的价电子数和σ轨道价电子数；σ、π分别为与该原子形成的σ和π轨道电子数；n、h分别为原子的孤对电子数和与该原子连接的氢原子数。

(2) 计算其他非氢原子对固有状态值I的影响，即求增量ΔIi

式中，i、j分别为相互影响的两非氢原子的编号；dij为第i和第j原子之间的拓扑距离。

(3) 将各个原子的固有状态 Ii与其他非氢原子的扰动ΔIi相加即得到分子中原子i的电性拓扑状态指数Si

(4) 将属于相同原子类型的各非氢原子的电性拓扑状态指数相加即得到各原子类型的 ETSI值，而各原子类型混合ETSI值为

式中，x1、x2分别为二元混合物中各组分所占的体积分数（x1+x2=1）。

2.2 SVM回归理论

支持向量机（support vector machine，SVM）采用VC维理论和结构风险最小化原则，可以较好地解决小样本、非线性、高维数、局部极小等问题。随着ε-不敏感损失函数的引入，已广泛应用于解决数据的回归问题，并表现出良好的预测性能[16]。

给定样本为(x1, y1), (x2, y2), …, (xk, yk)∈RN× R，其中 xi∈RN为输入参数，yi∈R为相应的输出参数，k为样本个数。SVM通过一个确定的非线性映射θ将输入数据x映射到高维特征空间F，并构建最优超平面将问题转化为线性回归分析，设回归函数为 f(x)=[w·θ(x)]+b，其中w为权值矢量，b为阀值。

根据统计学理论，考虑允许拟合误差的情况，可通过以下目标数极小化确定SVM的回归函数

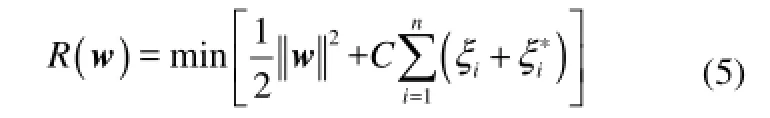
在样本数较少时，可利用拉格朗日方法求解上述约束最优化问题，将原问题转化为对偶问题，令参数w、b、的偏导数都等于零，即得

式中，K(xi, xj)是SVM核函数；αi、为二次规划问题的拉格朗日系数；n为支持向量机数。

核函数K(xi, xj)=[θ(xi), θ(xj)]，即得i=1

因此SVM最优回归函数表示为

目前SVM回归算法常用的核函数是径向基函数（radial basis function，RBF），可表示为

由SVM回归理论可知，RBF核函数的惩罚系数C、参数宽度γ以及ε-不敏感损失函数中ε的取值是影响SVM预测性能的关键参数，为获得最佳的模型预测精度和泛化能力，在建模过程中需要对SVM超平面参数进行寻优。

2.3 MPSO算法

改进的粒子群优化（modified particle swarm optimization，MPSO）算法引入指数递减惯性权重（exponential decreasing inertia weight，EDIW）和收敛因子来平衡 PSO算法的全局搜索与局部搜索能力，添加粒子自适应变异保持种群多样性，并选择训练集交叉验证下的均方差 MSE作为适应度函数，在提高标准粒子群算法对解空间的搜索能力的同时也保证了最终预测模型的精度[17]。

MPSO算法中的粒子通过个体极值Pbest和全局极值Gbest更新自身的速度和位置改进的速度、位置更新公式如下

Subject to

1

式中，k为当前迭代次数；kmax为最大迭代次数；w(k)为惯性权重指数函数；β为递减系数，默认取10；φ为收敛因子，由非负加速度因子c1、c2决定；α为约束因子；d=1,2,…,D，D为粒子维数。

选择交叉验证下的均方差MSE为适应度函数，计算公式如下

式中，yi,pred、yi,obs分别为训练样本的预测值和实验值；n为训练集样本数。

采用MPSO算法优化SVM超平面参数流程如图2所示。

图2　基于MPSO算法优化SVM参数流程Fig.2 Flowchart of optimizing SVM parameters based on MPSO algorithm

2.4 预测模型建立

2.4.1 MPSO-SVM 模型 采用 Lin等[18]开发的Libsvm3.20进行SVM回归运算。利用可燃混合液体所包含的9种不同原子类型对应的ETSI值对自燃温度进行表征，选择测得的168组自燃温度实验数据作为样本集，对样本集进行划分，随机抽取每组1个数据点作为测试集，共28个数据点作为测试集，用于对模型预测能力进行验证，其余140个数据点作为训练集，用于建立预测模型。

建模前应对训练集、测试集的输入和输出都进行归一化预处理，经过运算验证，归一化区间设为[-1,1]时，建模效果最好。设置SVM类型为ε-SVR；核函数类型为径向基RBF核；采用“留1/10法”交互验证（10-fold cross validation）结果作为参数寻优的标准；粒子数量为30，最大迭代次数Tmax=300；惯性权重wstart=0.9、wend=0.4；加速度因子c1=2.05，c2=2.05，即收敛因子φ=0.7298，约束因子α=1；C、γ、ε的搜索范围分别为[10-1,102]、[10-2,103]、[10-2,102]；速度和位置之间的关系式 V=kX，取k=0.6。确定SVM模型的最优参数:best C=14.9223，best γ=0.36202，best ε=0.01，根据SVM最优超平面参数建立MPSO-SVM预测模型。

2.4.2 MLR模型 多元线性回归（multiple linear regression，MLR）分析采用SPSS Statistics 22在95%置信区间内使用全回归算法进行MLR回归，获得的MLR预测模型如下

其中，复相关系数R2=0.942，F检验值f=235.14，模型标准误差SE=21.896，显著性概率p<0.001，说明该方程具有显著的统计学意义。

同时，对样本数据进行了主成分分析（principal component analysis，PCA），在95%的解释率下，有5个原子类型对自燃温度影响显著，分别是ssCH2> sOH > dO > sCH3> ssO。降维结果表明，各个原子类型之间存在较强的共线性问题，而直接简单地运用MLR建模并不是最佳的。

2.4.3 GSM-SVM 模型 网格搜索法（gird search method，GSM）是将待搜索参数在一定的空间范围中划分成网格，通过遍历网格中所有的点进行寻优。设置超平面参数 C、γ、ε的格点搜索范围分别为[2-10,210]、[2-10,210]、[20.1,210]，log2C、log2γ、log2ε对应的步长分别为1、1、0.1。确定SVM模型的最优参数:best C=16，best γ=0.0625，best ε=0.1，记为GSM-SVM模型。

2.4.4 GA-SVM模型 遗传算法（genetic algorithms，GA）是一类借鉴自然界遗传机制和生物进化论而成的并行随机化搜索算法[19]。设置种群数量Sizepop=20，最大进化终止代数Maxgen=150；选择概率pSelection=0.9，交叉概率pCrossover=0.4，变异概率pMutation= 0.02；C、γ、ε的搜索范围分别为[0,102]、[0,103]、[10-2,1]，采用二进制对参数编码。最终确定 SVM 模型的最优参数:best C=74.174，best γ=0.0572，best ε=0.0496，记为GA-SVM模型。

2.4.5 PSO-SVM模型 采用标准PSO算法来优化SVM的超平面参数C、γ、ε，设置粒子数量N=30，最大迭代终止次数Tmax=300；惯性权重w=0.9，加速度因子c1=2.05，c2=2.05，约束因子α=1；其余参数与MPSO算法一致。确定SVM模型的最优参数: best C=100，best γ=0.01，best ε=0.01，记为PSO-SVM模型。

2.5 模型验证和稳定性分析

模型验证（model validation，MV）是对模型的稳定性、预测及泛化能力的检验[20]。复相关系数R2用于衡量模型的拟合度，即用于模型建模能力的验证。模型的外部预测能力可通过对测试集进行外部验证，用交叉验证系数表示。平均绝对误差AAE，平均相对误差APE，均方根误差RMSE也可用来表示模型的性能。的计算公式为

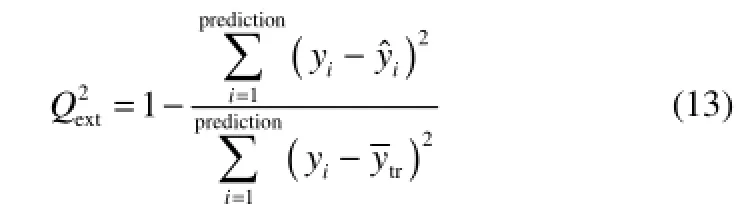
式中，yi、ŷi为测试样本的实验值和预测值；为训练样本实验值的平均值。

表3　模型的主要性能参数比较Table 3 Comparison among main statistical parameters of obtained models

由表3可知，MPSO-SVM模型复相关系数R2为0.991，外部验证系数为0.948，均大于0.9，说明模型具备良好的预测性能及泛化能力。同时，对测试集样本的平均绝对误差AAE为11.1 K，在自燃温度实验绝对误差允许范围内。其次，如图3所示，自燃温度模型预测值与实验值进行比较，训练集和测试集的数据点大部分落在图中所画实验值和预测值等值线上，没有太多数据点严重偏离等值线，说明MPSO-SVM模型的预测效果很好。

图3　MPSO-SVM模型自燃温度预测值与实验值的比较Fig.3 Comparison between predicted and experimental AIT values of MPSO-SVM model

图4　MPSO-SVM模型自燃温度预测残差Fig.4 Residuals versus experimental AIT values of MPSO-SVM model

2.5.2 模型稳定性分析 为了排除建模过程中的“偶然相关性”，确保模型的稳定性，对模型的预测残差进行分析，结果如图4所示，可知模型的预测残差均匀且随机地分布于零基准线的两侧，不存在明显的规律性，可推断出在建模过程中未产生系统误差，具有较强的稳定性。残差分析结果显示，随机选取的测试集数据中有个别数据点的预测误差高于或接近于均方根误差RMSE的3倍，属异常值。理论表明[21]，出现异常值的样本数量低于样本数的10%，可以通过剔除异常值样本来提高模型的相关性，重新建模后，新的模型复相关系数 R2达到了0.994，外部验证系数为0.951，模型性能更好。

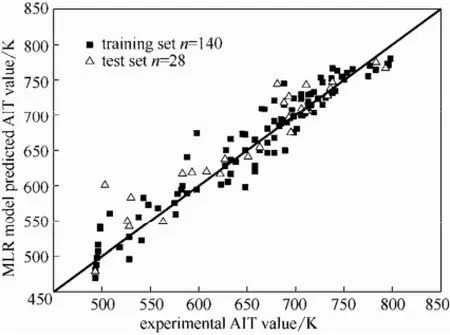
图5　MLR模型自燃温度预测值与实验值的比较Fig.5 Comparison between predicted and experimental AIT values of MLR model

图6　GSM-SVM模型自燃温度预测值与实验值的比较Fig.6 Comparison between predicted and experimental AIT values of GSM-SVM model

表4　测试集自燃温度模型预测值Table 4 Predicted AIT values for test set by obtained models

2.5.3 模型比较 图5～图8分别为MLR、GSMSVM、GA-SVM、PSO-SVM模型自燃温度预测值与实验值的比较分析结果。表4列出了各个模型测试集对应的自燃温度预测值。从误差角度来分析，MPSO-SVM模型预测性能最佳（以RMSE为标准）。从模型拟合效果来看，MPSO-SVM模型的复相关系数R2也明显优于其他模型。从表4同样可以看出MPSO-SVM模型预测效果最好。综上所述，MPSO-SVM模型具有较好的拟合效果，较强的泛化能力，可以很好地进行自燃温度的预测。

图7　GA-SVM模型自燃温度预测值与实验值的比较Fig.7 Comparison between predicted and experimental AIT values of GA-SVM model

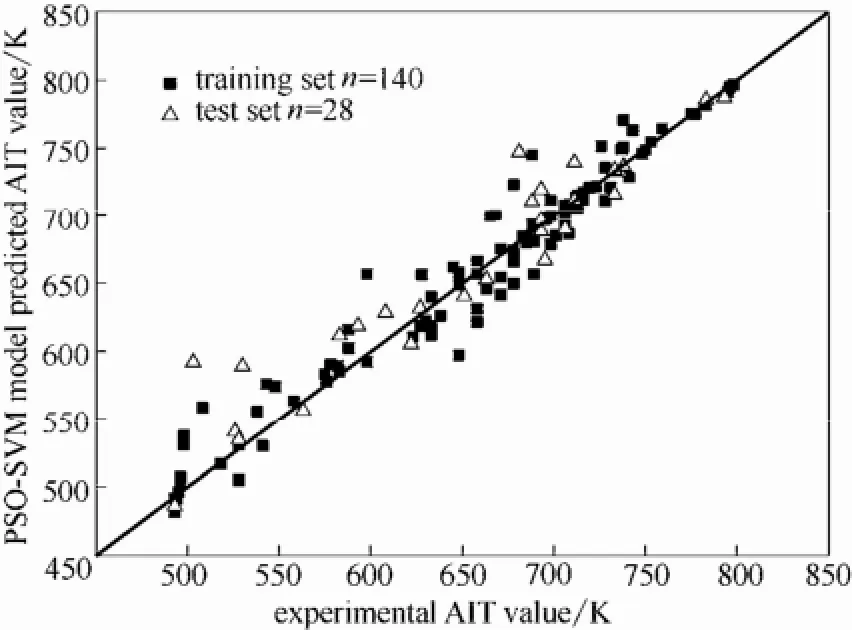
图8　PSO-SVM模型自燃温度预测值与实验值的比较Fig.8 Comparison between predicted and experimental AIT values of PSO-SVM model

为了确定MPSO-SVM模型中各原子类型的对自燃温度的贡献程度，根据描述符重要度衡量方法（method for measure of descriptor importance，MMDI）方法[22]对模型中9个输入原子类型的相对重要度进行了研究，所得各原子类型相对应的均方根误差（RMSE）增量，RMSE增量越大，即认为该原子类型对自燃温度的影响越大，各原子类型对应的RMSE增量见表5。根据表中RMSE增量的大小，各原子类型对自燃温度的重要度排列如下: ssCH2> sOH > dO > sCH3> ssO > ssdC > aaCH > sssCH > aasC。计算结果表明，MPSO-SVM模型与MLR模型的重要度分析吻合。

表5　MPSO-SVM模型各原子类型对应的RMSE增量Table 5 Increment in RMSE for each atomic types in MPSO-SVM model

3　结 论

（1）基于电性拓扑状态指数理论，建立 SVM模型来预测二元可燃混合液体自燃温度，并对各原子类型对自燃温度的重要度进行排序。

（2）提出改进的粒子群算法（MPSO）对SVM超平面参数C、γ、ε进行寻优，引入指数递减惯性权重和收敛因子来平衡 PSO算法的全局搜索与局部搜索能力，改进效果显著。

（3）将MPSO-SVM模型与MLR、GSM-SVM、GA-SVM、PSO-SVM模型进行比较，结果表明，在获得的混合自燃温度数据（含9种原子类型）的范围内，MPSO-SVM模型性能最优。

（4）利用电性拓扑状态指数理论建立简单可靠的适用于9种原子类型的二元完全互溶体系混合自燃温度预测模型，为工程上提供了一种快速预测混合物质自燃温度的有效途径。

References

[1] 张宏哲, 王宁, 王亚琴, 等. 活化温度对活性炭自燃危险性的影响[J]. 化工学报, 2012, 63(11): 3730-3735.

ZHANG H Z, WANG N, WANG Y Q, et al. Influence of activation temperature on spontaneous ignition behavior of activated carbon [J]. CIESC Journal, 2012, 63(11): 3730-3735.

[2] YEONG S K, SUNG K L, JAE H K, et al. Prediction of autoignition temperatures (AITs) for hydrocarbons and compounds containing heteroatoms by the quantitative structure-property relationship [J]. Journal of the Chemical Society, Perkin Transactions 2, 2002, 12: 2087-2092.

[3] PAN Y, JIANG J C, WANG R, et al. Advantages of support vector machine in QSPR studies for predicting auto-ignition temperatures of organic compounds [J]. Chemometrics and Intelligent Laboratory Systems, 2008, 92(2): 169-178.

[4] PAN Y, JIANG J C, WANG R, et al. Predicting the auto-ignition temperatures of organic compounds from molecular structure using support vector machine [J]. Journal of Hazardous Materials, 2009, 164(2/3): 1242-1249.

[5] TSAI F, CHEN C, LIAW H. A model for predicting the auto-ignition temperature using quantitative structure property relationship approach [J]. Procedia Engineering, 2012, 45: 512-517.

[6] BAGHERI M, BORHANI T N G, ZAHEDI G. Estimation of flash point and auto-ignition temperature of organic sulfur chemicals [J]. Energy Conversion and Management, 2012, 58(6): 185-196.

[7] KONG D, ECKHOFF R K, ALFERT F. Auto-ignition of CH4/air, C3H8/air, CH4/C3H8/air and CH4/CO2/air using a 1 L ignition bomb [J]. Journal of hazardous materials, 1995, 40(1): 69-84.

[8] ROTA R, ZANOELO E F. Prediction of the auto-ignition hazard of industrial mixtures using detailed kinetic modeling [J]. Industrial and Engineering Chemistry Research, 2003, 42(13): 2940-2945.

[9] NORMAN F, VAN DEN SCHOOR F, VERPLAETSEN F. Auto-ignition and upper explosion limit of rich propane-air mixtures at elevated pressures [J]. Journal of Hazardous Materials, 2006, 137(2): 666-671.

[10] VAN DEN SCHOOR F, NORMAN F, VANDEBROEK L, et al. A numerical study of the influence of ammonia addition on the auto-ignition limits of methane/air mixtures [J]. Journal of Hazardous Materials, 2009, 164(2/3): 1164-1170.

[11] American Institute of Chemical Engineers (AIChE). Design Institute for Physical Properties (DIPPR) [EB/OL]. [2014-09-11]. http://www.aiche.org/dippr/projects/801.

[12] International Safety Intergovernmental Organization. International Chemical Safety Cards (ICSCs) [EB/OL]. [2010-03-11]. http://www.i-nchem. org/pages/icscs.html.

[13] 蒋军成, 潘勇. 有机化合物的分子结构与危险特性[M]. 北京: 科学出版社, 2011: 231-248.

JIANG J C, PAN Y. The Molecular Structure and Dangerous Properties of Organic Compounds [M]. Beijing: Science Press, 2011: 231-248.

[14] KIER L B, HALL L H. An electro-topological state index for atoms in molecules [J]. Pharmaceutical Research, 1990, 7(8): 801-807.

[15] HALL L H, KIER L B. Electro-topological state indices for atom types: a novel combination of electro-topological and valencestate information [J]. Journal of Chemical Information and Computer Sciences, 1995, 35(6): 1039-1045.

[16] 安剑奇, 陈易斐, 吴敏. 基于改进支持向量机的高炉一氧化碳利用率预测方法[J]. 化工学报, 2015, 66(1): 206-214.

AN J Q, CHEN Y F, WU M. A prediction method for carbon monoxide utilization ratio of blast furnace based on improved support vector regression [J]. CIESC Journal, 2015, 66(1): 206-214.

[17] 张晓南, 刘安心, 刘斌, 等. 基于优化PSO-SVM模型的软件可靠性预测[J]. 计算机应用, 2011, 31(7): 1761-1764, 1772.

ZHANG X N, LIU A X, LIU B, et al. Software reliability prediction based on improved PSO-SVM model [J]. Journal of Computer Applications, 2011, 31(7): 1761-1764, 1772.

[18] CHANG C C, LIN C J. LIBSVM: a library for support vector machines [J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 389-396.

[19] 王梦寒, 李雁召, 夏知姿, 等. 基于 Kriging模型与遗传算法结合的 RHCM 成型工艺参数优化[J]. 化工学报, 2014, 65(12): 5054-5060.

WANG M H, LI Y Z, XIA Z Z, et al. Processing parameters optimization of rapid heat cycle molding based on Kriging meta-model and genetic algorithm [J]. CIESC Journal, 2014, 65(12): 5054-5060.

[20] GRAMATICA P, PILUTTI P, PAPA E. Validated QSAR prediction of OH tropospheric degradation of VOCs: splitting into training_test sets and consensus modeling [J]. Journal of Chemical Information and Computer Sciences, 2004, 44(5): 1794-1802.

[21] LIPNICK R L. Outliers: their origin and use in the classification of molecular mechanisms of toxicity [J]. Science of the Total Environment, 1991, 109: 131-153.

[22] 潘勇. 有机物定量结构燃爆特性相关性及预测模型研究[D]. 南京:南京工业大学, 2009.

PAN Y. Research on prediction models and quantitative relationships between the structures and flammability characteristics of organic compounds [D]. Nanjing: Nanjing University of Technology, 2009.

2015-12-02收到初稿，2016-04-06收到修改稿。

联系人:蒋军成。第一作者:何凡（1991—），男，硕士研究生。

Received date: 2015-12-02.

中图分类号:O 621.2；X 937

文献标志码:A

文章编号:0438—1157（2016）07—3109—09

DOI:10.11949/j.issn.0438-1157.20151811

基金项目:国家自然科学基金项目（21436006，21576136）；江苏省自然科学基金重大项目（12KJA620001）。

Corresponding author:Prof. JIANG Juncheng, j_c_jiang@163.com supported by the National Natural Science Foundation of China (21436006, 21576136) and the Major Project of the Natural Science Foundation of Jiangsu Province (12KJA620001).

Prediction of auto-ignition temperatures for binary liquid mixtures based on electro-topological state indices

HE Fan, JIANG Juncheng, PAN Yong, NI Lei
(Jiangsu Key Laboratory of Hazardous Chemicals Safety and Control, College of Safety Science and Engineering, Nanjing Tech University, Nanjing 210009, Jiangsu, China)

Abstract:The auto-ignition temperature (AIT) values of 168 sets of binary flammable liquid mixtures composed of different components and volume ratios were measured by AITTA 551 auto-ignition temperature tester. The mixed electro-topological state indices (ETSI) values of different atom types were calculated. The modified particle swarm optimization (MPSO) algorithm with exponential decreasing inertia weight (EDIW) was applied to optimize the support vector machine (SVM) hyper-parameters and MPSO-SVM prediction model was established. The model was employed in research for predicting the AIT of mixtures according to the mixed ETSI values of different atom types. The results showed that it could effectively predict the AIT of binary liquid mixtures based on electro-topological state indices. The squared correlation coefficient (R2) and average absolute error (AAE) of MPSO-SVM model were 0.991 and 3.962 K, respectively. In terms of model generalization performance and prediction accuracy, the result of MPSO-SVM model was obviously superior to the results of multiple linear regression (MLR), grid search method (GSM-SVM), genetic algorithm (GA-SVM) and particle swarm optimization (PSO-SVM). This study provided an effective method to predict the AIT of binary liquid mixtures for engineering.

Key words:electro-topological state indices; binary mixture; algorithm; auto-ignition temperature; prediction