炼化装置故障链式效应定量安全预警方法
2016-08-06胡瑾秋张来斌王安琪
胡瑾秋,张来斌,王安琪
炼化装置故障链式效应定量安全预警方法
胡瑾秋,张来斌,王安琪
(中国石油大学(北京)机械与储运工程学院,国家安全生产技术支撑体系“油气生产事故预防与控制基础研究实验室”,北京 102249)
摘要:炼化装置故障及其故障链式效应对油气生产和人民生命安全所造成的危害严重。从故障链角度进行事故风险研究,提出炼化装置故障链式效应定量安全预警方法。首先分析炼化装置故障链式关系结构,基于目标树成功树-动态主逻辑图(GTST-DMLD)建立其故障链式效应关系模型,揭示炼化装置故障链式效应行为规律和关联本质,从而评价装置异常工况下的安全状态。进一步以马尔可夫过程为理论基础,建立故障链式效应预测模型,预测故障传播的后果和方向,并计算各后果的发生概率,为现场操作人员进行主动维修或应急处置提供依据。案例分析中通过对某化工厂常压塔装置、减压炉装置为研究对象进行应用与验证,结果表明该方法可以准确地对系统故障发生后的状态进行评价和预测,方法有效、可行,便于操作人员在处置已有故障的同时,注意预防其他异常工况的发生,降低油气生产加工过程中的整体风险。
关键词:过程系统;目标树成功树-动态主逻辑图;故障链式效应;安全;预测
引 言
在油气生产与加工领域,过程安全受到当今世界的广泛关注。其安全问题区别于其他行业有几大不同的特征[1]:(1)物料大多具有易燃易爆性、反应活性、毒性和腐蚀性;(2)生产装置规模大、集成度高,且生产过程具有强非线性;(3)系统组成关系与行为复杂,以及与其环境之间的关联程度高、耦合性强,导致系统故障的形成、传播、演化等故障行为具有多样性、随机性、涌现性等特点。
作为一种复杂高阶非线性动态系统,炼化装置安全事故大多是由于系统的“变化”所引起的,例如液位偏高、流量过大、机泵故障等。这种“变化”可能是自发的,可也能是外部作用的结果。如果由于这些“变化”使系统的运行工况超出设计预期的安全范围,则可能出现操作问题或系统故障。单一设备或工艺过程出现故障或偏差,极易借助生产系统之间的相互依存、相互制约关系,产生连锁效应,由一种故障引发出一系列的故障甚至事故、灾害,同时从一个地域空间扩散到另一个更广阔的地域空间,这种呈链式有序结构的故障(或异常事件)传承效应称为故障链[2],所造成的危害和影响远比单一故障事件大而深远。
目前越来越多的专家学者由单一故障的研究转向对故障链的研究[3-6]。然而故障链的复杂性是构建有效的安全预警系统的主要障碍,它不仅由外部环境(包括人为因素)所致,更主要的是生产系统支配层次上的链式关系引起的,既有一因一果,又有一果多因、一因多果、多因多果、果果相连等[7]。故障链的主线是故障或偏差的相继引发过程,系统故障的链式特征决定了若只考虑一个单体故障过程则无法全面反映系统完整的事故剧情和受损情况。
另一方面,大部分炼化生产过程采用了DCS、SCADA等监控系统,当生产过程处于常规(正常)状态时,现场操作人员依靠监控系统使生产处于平稳和安全状态。然而,除了正常状态以外,生产过程还包括过渡状态、异常状态、事故状态、灾难状态等。一旦出现非正常状态,甚至是事故状态,常规的监控系统往往无能为力,需要现场操作人员根据对过程的了解和生产经验做出及时判断,采取合理的措施使生产过程重回正常状态。但对于复杂的过程,面对海量杂乱无章的数据,加之故障链式效应的逐级扩大,操作人员根本无法及时做出判断和维修决策,甚至有可能产生误导,做出错误的决策[8]。据统计,在发生的事故中,其中约有70%是由于操作失误引起的。因此亟需建立炼化生产过程故障预警方法,对非正常工况及其故障传播情形下系统的安全状态进行准确评价和预测,为操作人员进行维修决策和应急处置提供合理的依据。
国内外对故障因果关系的分析方法主要可分为两大类,一类是基于图论技术的故障或危险剧情表达方法,具有代表性的包括SDG法[9]、Petri网络法[10-11]、动态贝叶斯网络法(DBN)[12-14]等;另一类是基于过程信息和事故案例的“专家系统”方法[15]。此外,基于小世界聚类特性的故障传播模型[16]可以在无法准确获得故障之间的因果逻辑关系情况下(大部分实际情况确实如此),分析故障发生、传播和放大的根本原因,计算扩散强度,找出系统中的脆弱点。该模型在电力系统故障分析中应用良好,而在其他工业领域鲜有提及,其原因是电力系统自身具有明确的拓扑结构特性,可以方便地转化为小世界网络,而油气加工等多数复杂系统自身故障传播的结构特点不明确,具有较大随机性,且其故障传播是否具有小世界特性至今尚未得到证明[17]。
因此,结合炼化装置故障传播的多样性、随机性和涌现性等特点,将上述方法应用在炼化装置安全预警领域时,存在以下一些局限性。
(1)较多采用定性或半定量分析,且适用于连续系统,模型节点局限于具体参数,对炼化装置种类繁多的异常状态的表达能力十分有限。
(2)无法定量表征系统在故障条件下整体的安全状态,而该信息对过程安全的预警和应急处理却十分重要,因为繁杂的局部故障信息将对指挥人员做出合理、迅速的应急决策产生干扰。
(3)“专家系统”方法需要对被评价系统的信息作详细描述,知识范围大,信息获取和维护费时费力。更大的困难在于,当突发事件超出了经验和案例的知识范畴,将无法给出结果;即便从知识本体[18]角度能够计算出推理结果,但对于影响因素错综复杂的实际生产系统,却很难对其推理结果给出合理解释。而在突发事故应急指挥时,对推理结果的准确解释将十分重要。
针对上述问题,本文从故障链角度进行事故风险研究,提出炼化装置故障链式效应定量安全预警方法。首先分析系统故障链式关系结构,建立基于目标树成功树-动态主逻辑图(goal tree success tree-dynamic master logic diagram,GTST-DMLD)的故障链式效应关系模型,揭示其链式效应行为规律和关联本质,从而评价炼化装置异常工况下的安全状态。进一步以马尔可夫过程为理论基础,建立故障链式效应预测模型,预测故障传播的后果和方向,并计算各后果的发生概率,为现场操作人员进行主动维修或应急处置提供依据。
1 炼化装置故障链式效应建模理论基础
1.1 目标树成功树-动态主逻辑图
目标树成功树-动态主逻辑图(GTST-DMLD)是一种针对系统功能和行为的图形化的建模方法,以图形化的方法来表达复杂系统,进而确定复杂系统的目标、功能及其物理组成元素之间的逻辑关系。
GTST-DMLD建模方法由两部分组成,分别是目标树成功树(goal tree success tree, GTST)、以及动态主逻辑图(dynamic master logic diagram, DMLD)。该建模方法由最初的 GTST开始不断演化、发展成为现在的 GTST-DMLD[19-20]。GTSTDMLD是描述复杂系统的物理行为与知识库的有效方法,并能够通过具有特定含义的符号将这些不同模式的因果传播关系进行表达与描述[21]。常用的符号及其含义见表1,典型的GTST-DMLD模型结构如图1所示。
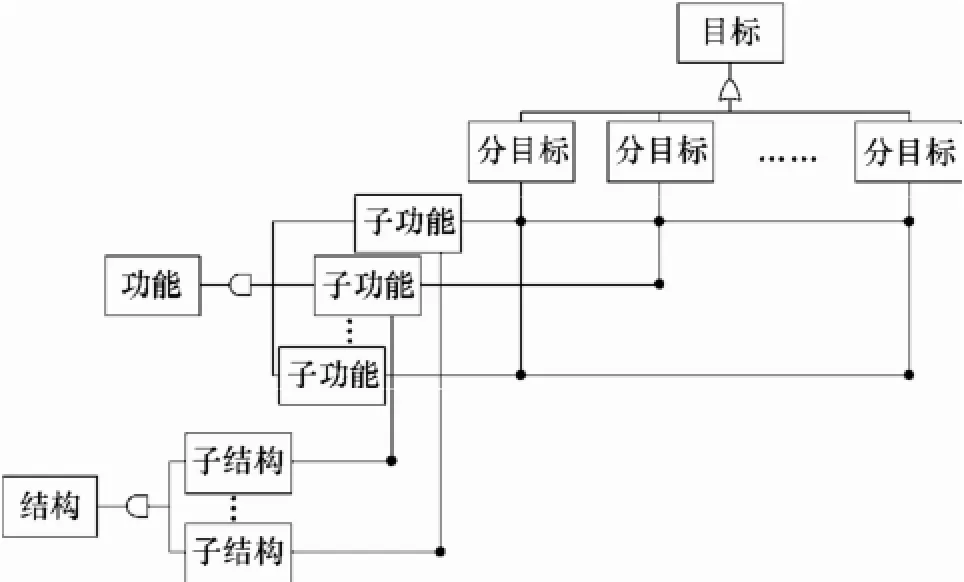
图1 典型GTST-DMLD模型结构Fig. 1 Typical structure of GTST-DMLD model
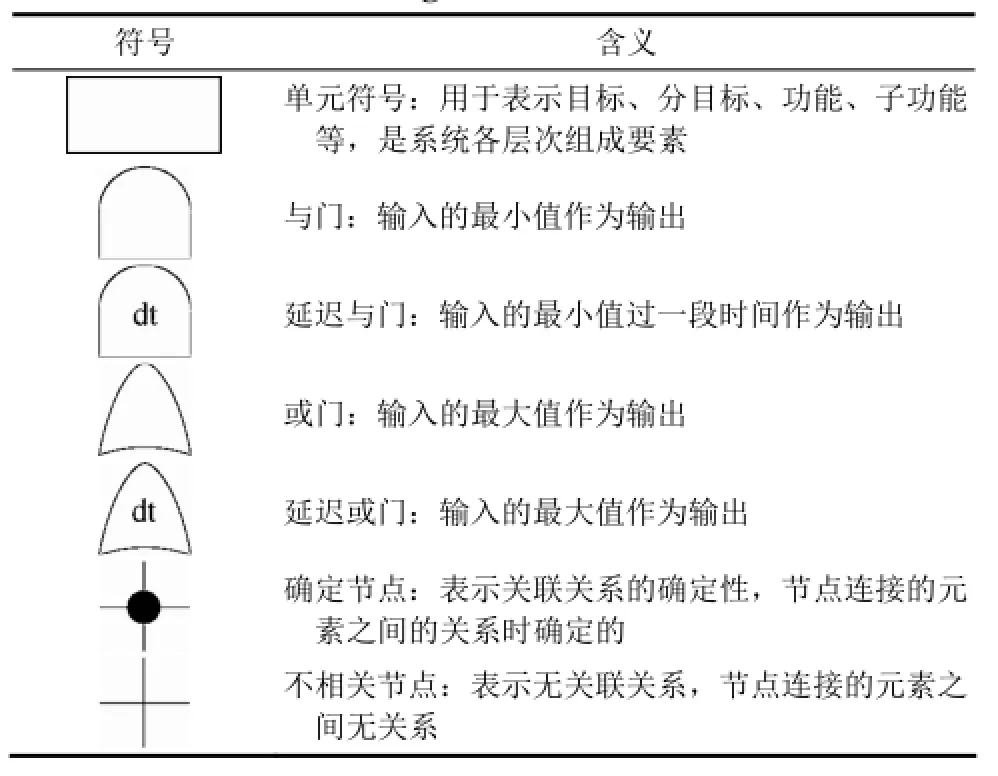
表1 GTST-DMLD建模符号Table 1 Modeling notation of GTST-DMLD
1.2 基于马尔可夫过程的故障预测理论基础
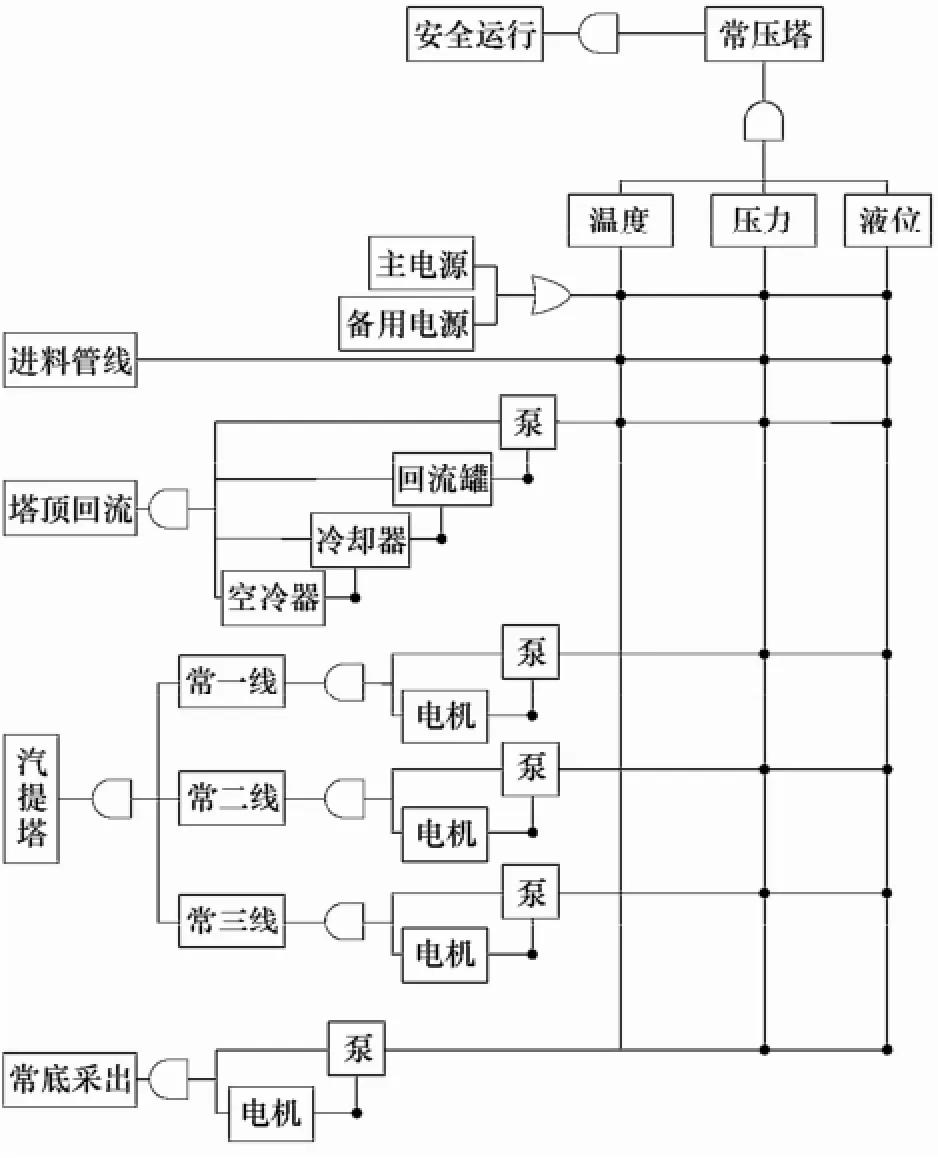
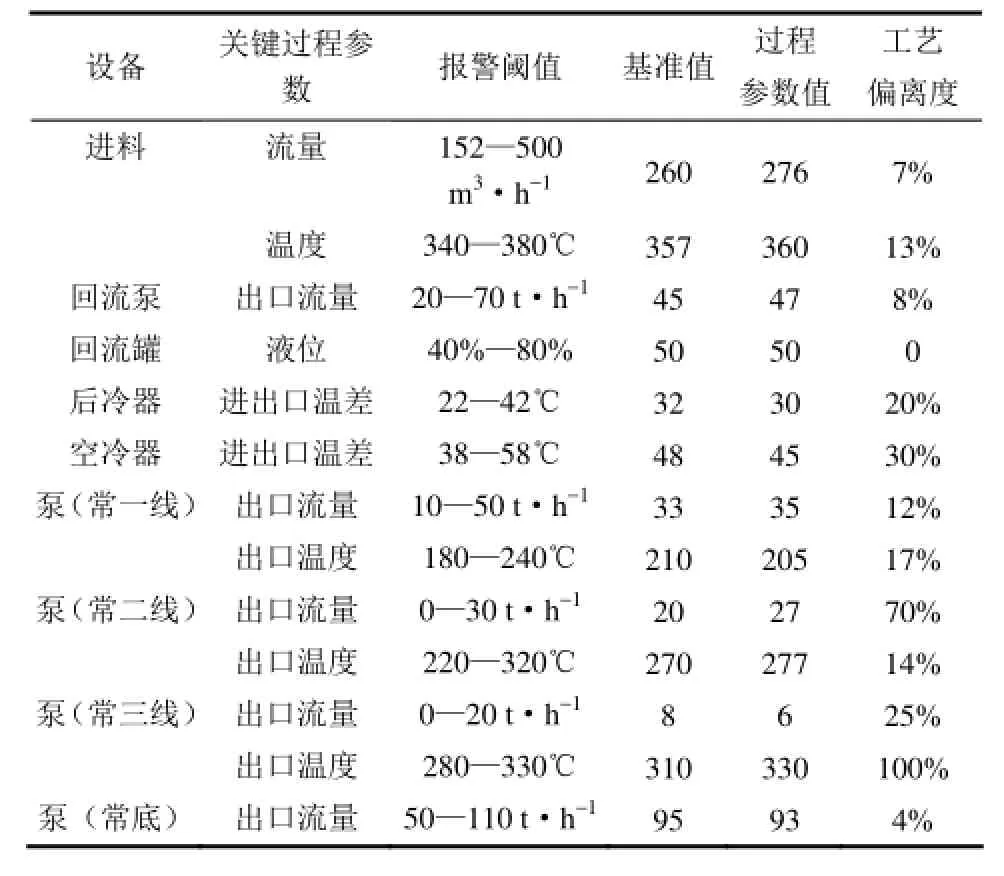
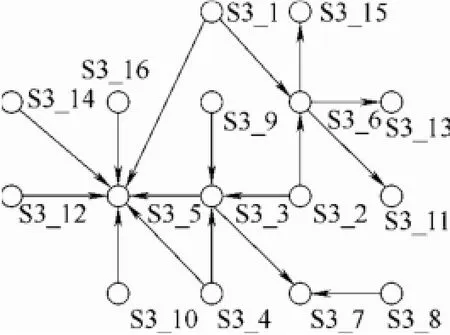
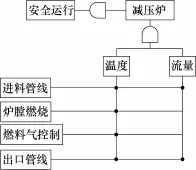
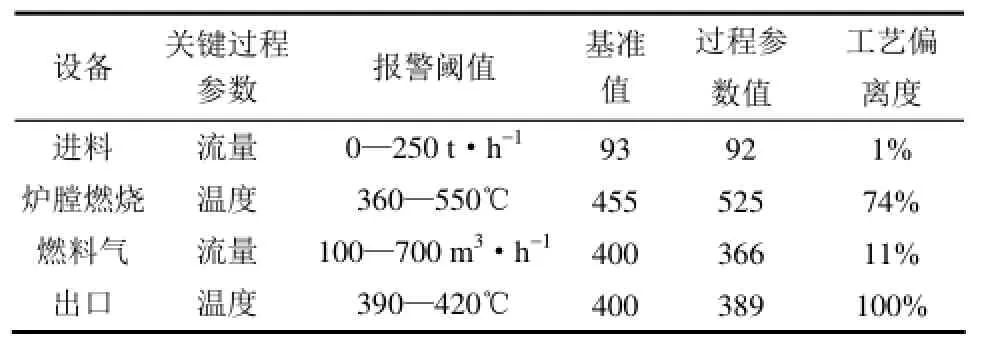
马尔可夫过程是一种重要的随机过程。其定义为:给定的随机过程{Xt,t∈T},如果过程的条件分布函数存在,且对任意n个时刻ti,i=1,2,…,n,t1 马尔可夫过程具有这样的特性“在已知目前状态(现在)的条件下,它未来的演变(将来)不依赖于它以往的演变(过去)”。即马尔可夫过程在当前时刻的状态与 tn-1时刻前的状态没有关系,只与tn-1时刻的状态有关系。上述性质称为马尔可夫过程的无后效性。在炼化装置中,多数异常事件、故障的传播关系可以用马尔可夫过程来描述,如控制截断阀门、紧急放空阀故障,将导致工艺过程窜压、憋压,进而使物料的化学物理反应发生偏差,轻者影响物料的净化处理质量,严重的将导致反应失控、装置发生泄漏或爆炸等过程。 马尔可夫过程的时间参数、状态参数可以是离散的,也可以是连续的。时间、状态均离散的马尔可夫过程也被称为马尔可夫链。对于炼化装置故障链式关系,由于其安全监测、检测获取的数据是按照一定的时间间隔存储的,故其马尔可夫模型属于马尔可夫链。对于离散马尔可夫过程,称矩阵为马尔可夫过程在m时刻的k步转移矩阵,如式(2)所示。 炼化装置故障链式效应定量安全预警方法从前期离线建模和后期实时预警角度(时间角度)分为两个过程;从现状评价和后果预测角度(功能角度)又可分为两个阶段。流程如图2所示。 图2 炼化装置故障链式效应定量安全预警方法实施流程Fig. 2 Implementation process of quantitative safety early warning method of fault propagation 从时间角度方法分为以下两个过程。 过程 1 前期离线建模过程,包括炼化装置工作流程分析、用建模符号语言描述子系统和目标之间的关系,最后建立炼化装置的GTST-DMLD基础模型。 过程 2 在线实时监测预警过程,包括 DCS实时状态监测、如发现参数异常,计算过程安全偏离度,进而计算系统的安全系数。当安全系数较低,发布预警信息,确定故障根原因,同时计算推理未来可能发生的异常,并行计算其发生概率。因此,本文预警功能的实时实现,主要体现在上述过程2。 从功能角度方法分为以下两个阶段。 阶段 1 基于 GTST-DMLD的系统安全性评价。即在故障或异常事件出现之后,实时评价炼化装置当前所处的安全状态,并计算得出系统的安全系数,为现场操作人员进行故障处置提供依据。 阶段 2 基于马尔可夫过程的故障链式传播后果预测。即预测故障发生以后系统的运行情况,揭示故障发生之后会产生哪些后果,并给出这些后果的发生概率,为现场操作人员进行事故应急准备提供依据。 2.1 基于目标树成功树-动态主逻辑图的炼化装置安全性评价 (1)建立炼化装置的GTST-DMLD模型 (Ⅰ)分析所研究的炼化装置的工作流程,确立系统运行的目标和达到这个目标需要的功能。如主目标为系统安全运行,为了达到安全运行这一目标,炼化装置需要有保持温度稳定、保持压力稳定、保持液位稳定、保持流量稳定等功能。 (Ⅱ)将该炼化装置按照工艺流程划分为子系统,如初馏塔可以划分为进料子系统、塔顶回流子系统、初侧采出子系统及初底采出子系统。 (Ⅲ)使用表 1中的建模符号语言描述子系统和目标之间的关系,建立该炼化装置GTST-DMLD基础模型。 (Ⅳ)将子系统进一步拆分成单独的设备,继续使用表1中的建模符号语言描述这些设备和子系统之间的关系,同时更新上一步(Ⅲ)中建立的GTST-DMLD基础模型中的相关模块。 (2)选取关键过程参数 根据步骤1建立GTST-DMLD模型时划分的子系统,为子系统中的每个设备选择关键工艺过程参数,常见的关键工艺过程参数选择见表2。 (3)计算过程安全偏离度 表3 关键过程参数Table 2 Key process parameter 现场状态监测系统(如 DCS、MES等)实时采集过程参数信息,并采用下列方法实时计算过程安全偏离度。 基于模糊理论评估设备的安全状态,用“过程安全偏离度”来描述过程参数实际值与设计值(或正常值)之间偏离的程度,以反映故障的严重程度。过程安全偏离度的计算公式如式(3)所示。 其中,基准数值的选取使用如下的方法:炼化装置在设计阶段已规定工艺流程参数的操作范围,如换热终温、初馏塔进料温度等。对于在役装置,若这些参数在设计阶段已确定并在设备运行过程中可准确获取,则在计算中将这些数值作为基准数值。若在没有或者无法获取某些参数对应的基准数值的情况下,可以将报警阈值的上下限取一个平均值,将该平均值作为基准数值进行计算。其中报警值的选取使用如下的方法:当过程参数值低于基准值时,报警值选择阈值下限;当过程参数值高于基准值时,报警值选择阈值上限。该计算过程虽带有一些主观不确定性,但在工程应用中已能满足其要求和精度。后续的研究仍然会进一步提升该环节的客观性和智能化。 图3 过程安全偏离度隶属度函数Fig. 3 Membership function of process safety 当过程安全偏离度为0时,即过程参数稳定,没有发生故障的可能性;当过程安全偏离度为100%及以上时,即过程参数发生较大变化,系统严重故障;数值落在此区间内,系统具有一定程度的危险隐患,需开展下一步骤的计算,从而对系统安全状态进行细化评价。 (4)基于模糊语言评价系统的安全状态 根据步骤(3)中计算的过程安全偏离度,定义设备安全状态的模糊集合:设备状态={正常,轻微故障,故障}。根据历史数据和专家经验确定设备安全状态的隶属度函数如图3所示,在本文中,当工艺偏离度在0~50%时,认为设备处于正常状态;当工艺偏离度在20%~100%时,认为设备处于轻微故障状态,工艺偏离度为70%时对轻微故障的隶属度为1;当工艺偏离度在70%以上时,认为设备处于故障状态。 其中的一个关键点是上述隶属度函数参数的选取。一般炼化企业现场均安装有实时监测和报警处理系统,建议将数据偏差值、报警数据以及现场维检修记录结合起来,经多年大量的数据统计分析,从而确定图3中的隶属度函数参数,保证该模型的客观性和准确性。 (5)计算系统对各个状态的隶属度 在计算得出设备关键过程参数的过程安全偏离度之后,通过隶属度函数计算得出设备、装置对各个状态(正常、轻微、故障)的隶属度。然后根据表3所列出的推理规则,确定上级装置、子系统对各个状态的隶属度,隶属度使用“最小-最大法”确定,计算公式如式(4)、式(5)所示。 其中,X、Y为模糊集合元素,u(X)、u(Y)表示隶属度,在计算“与”这一逻辑关系时使用式(4),计算“或”这一逻辑关系时使用式(5)。 表3 安全状态推理规则Table 3 State inference rule (6)计算系统的安全系数 使用解模糊公式将模糊集合进行量化,如式(6)所示。 其中,wi表示模糊集合中元素xi的隶属度,yi为xi的参考值。设定正常的参考值为100%,轻微故障的参考值为50%,故障的参考值为10%。将系统的状态分为4个等级:非常危险、危险、一般、好,各个等级与安全系数的对应关系见表4。 表4 系统安全状态评价标准Table 4 Safety level evaluation standard 2.2 基于马尔可夫过程的炼化装置故障预测 故障在炼化装置中动态传播过程的马尔可夫模型如图4所示,其中λ1,2表示状态S1向状态S2转移的概率,λ1,1表示状态 S1不发生迁移的概率,其他的以此类推。 图4 故障传播马尔可夫模型Fig. 4 Markov model of fault propagation 基于马尔可夫过程的故障预测流程如下。 (1)在炼化装置GTST-DMLD模型基础上,分析炼化装置中过程参数之间的作用关系,建立故障传播马尔可夫模型。 (2)为步骤(1)所建立的故障传播马尔可夫模型确定转移矩阵。通常根据装置长周期运行状态监测记录的历史数据计算的各模型对应的转移矩阵,并设定转移概率的实际含义为系统在10 min内从某状态转移到另一状态的概率。其中,预测的时间间隔(Tinterval)是可以根据实际需要设置的。在本文案例中,前期与现场操作人员沟通,共同确定为Tinterval=10 min。后期,若现场希望增加或缩短间隔时间,模型中可直接修改。 (3)进行系统故障预测。以故障的根原因为起点,在模型中寻找可能发生的异常,同时并行计算其发生概率,发布预警信息。 3.1 案例1:常压塔装置故障安全预警 故障场景:某炼厂常压塔装置于2014年2月某一时刻发生常三线馏出温度偏高的故障。根据本文所述方法,结合该实际案例具体数据,对该方法的应用有效性及其效果进行验证。按照本文第2节阐述的实施步骤,具体分析过程如下。 (1)建立炼化装置GTST-DMLD模型 经过分析将常压塔划分为电源、进料、塔顶回流、汽提塔、常底采出5个子系统,其中汽提塔又分为常一线、常二线及常三线3个子系统,建立的常压塔GTST-DMLD模型如图5所示。 (2)关键过程参数选取及过程安全偏离度计算 参考表2中所示的过程参数并根据该案例涉及的常压塔的实际运行工况,选取,常压塔的关键过程参数,如表5所示。在发生常三线馏出温度偏高故障的情况下,根据式(3)计算过程安全偏离度,计算结果见表5。 图5 案例1涉及的常压塔的GTST-DMLD模型Fig 5 GTST-DMLD model of atmospheric tower 表5 常三线馏出温度偏高情况下过程安全偏离度Table 5 Process safety deviation degree under fault condition (3)设备状态模糊化 根据过程安全偏离度和隶属度函数计算各个设备的安全状态隶属度,如表6所示。 (4)系统安全系数计算及评价 由GTST-DMLD模型可知,塔顶回流子系统中各个装置的连接方式为串联,逻辑“与”的关系,计算时先计算空冷器与后冷器,再计算空冷器与后冷器的子系统与回流罐,进而计算得出整个塔顶回流子系统的隶属度,最终计算得出的塔顶回流子系统对正常、轻微故障、故障状态的隶属度为{0.67,0,0}。 表6 设备安全状态隶属度Table 6 Safety state membership degree of each equipment 进料子系统对正常、轻微故障、故障状态的隶属度为{1,0,0};常一线对正常、轻微故障、故障状态的隶属度为{1,0,0};常二线对正常、轻微故障、故障状态的隶属度为{0,1,0};常三线对正常、轻微故障、故障状态的隶属度为{0,0,0.83};常底对正常、轻微故障、故障状态的隶属度为{1,0,0}。按照上述方法计算得出常压塔对正常、轻微故障、故障状态的隶属度为{0,0,0.83}。 使用式(6)计算常压塔的安全状态为(0×100%+0×50%+0.83×10%)/(0+0+0.83)= 10%,根据表4判别标准可知,常压塔处于“非常危险”的状态。 (5)过程参数作用关系分析并建立马尔可夫模型 根据常压塔GTST-DMLD模型,对过程参数之马尔可夫模型,如图6所示,图中各个节点的含义如表7所示。 (6)确定转移矩阵 通常根据装置长周期运行状态监测记录的历史数据,辅以专家及现场人员经验,计算常压塔故障传播马尔可夫模型转移矩阵如表8所示,由于空间有限,表8中的标号采用简写,如表第1行与第1列中的表头数字1代表节点S3_1,其他表头数字含义同理。 图6 常压塔故障传播马尔可夫模型Fig. 6 Markov model of fault propagation in atmospheric tower 表7 常压塔故障传播马尔可夫模型节点信息表Table 7 Node information of Markov model of fault propagation in atmospheric tower (7)故障预测 经现场排查,该故障的根原因为常压塔进料温度偏高,因此在马尔可夫模型中表示为节点 S3_2异常。由模型计算可能发生异常的节点为 S3_3、S3_6,且将进一步传播至节点S3_5,即常压塔顶温度、常压塔底温度,进而影响至常压塔底液位。使用马尔科夫模型进行发生概率计算,结果如表9所示。由表 9可知短时间内影响最大的节点为S3_6,常压塔底温度将发生异常。若不及时进行故障处置,节点S3_5也将在50分钟内出现异常,应急时需要注意监测常压塔底液位,并做好相应的处置准备。 3.2 案例2:减压炉装置故障安全预警 故障场景:该炼厂2014年3月某日减压炉装置发生减压炉出口温度偏低的故障。与案例1相同的分析过程不重复赘述。 减压炉的GTST-DMLD模型如图7所示。减压炉可以划分为进料、炉膛燃烧、燃料气控制及出口4个子系统。 根据式(3)计算过程安全偏离度,系统中各个装置关键过程参数的数值及计算出的工艺偏离度如表10所示。根据过程安全偏离度和图3所示隶属度函数计算出的各个设备的隶属度见表11。 表8 常压塔故障传播马尔可夫模型转移矩阵Table 8 Transition matrix of Markov model of fault propagation in atmospheric tower 图7 减压炉的GTST-DMLD模型Fig. 7 GTST-DMLD model of vacuum furnace 表11 设备安全状态隶属度Table 11 Safety state membership degree of each equipment 表9 各相关节点故障状态发生概率预测Table 9 Predicted fault occurrence probability of each related node 由GTST-DMLD模型(图7)可知,减压炉中各个子系统的连接方式为串联,逻辑“与”的关系,先计算进料与炉膛燃烧的安全状态隶属度,再计算进料与炉膛燃烧子系统与燃料气的,进而计算得出整个塔顶回流子系统的安全状态隶属度,最终计算得出减压炉系统整体关于正常、轻微故障、故障状态的隶属度为{0,0,0.87}。 计算减压炉的安全状态为(0×100%+ 0×50%+0.87×10%)/(0+0+0.87)=10%,根据表4判别标准可知,减压炉处于“非常危险”的状态。 图8 减压炉故障传播马尔可夫模型Fig. 8 Markov model of fault propagation in vacuum furnace 图8为减压炉的故障传播马尔可夫模型,图中各个节点的含义如表12所示,减压炉故障传播马尔可夫模型转移矩阵见表13所示。 表10 减压炉出口温度偏低故障情况下过程安全偏离度Table 10 Process safety deviation degree under fault condition 表12 减压炉故障传播马尔可夫模型节点信息Table 12 Node information of Markov model of fault propagation in vacuum furnace 表13 减压炉故障传播马尔可夫模型转移矩阵Table 13 Transition matrix of Markov model of fault propagation in vacuum furnace 经现场排查,该故障的根原因为减压炉燃料气流量偏低,在马尔可夫模型中表示为节点 S2_3异常,由模型推理知可能发生异常的节点为S2_2,即减压炉炉膛温度偏低,使用马尔科夫模型进行发生概率计算结果见表14所示。由表14可知炉膛温度发生异常概率在0.8以上,发布预警信息,在处置故障的同时需要注意控制炉膛温度,以减少故障的影响。 表14 相关节点故障状态发生概率预测Table 14 Predicted fault occurrence probability of related node (1)鉴于炼化装置部件及其与环境之间的关联程度高、耦合性强,导致系统故障的形成、传播、演化等故障行为具有多样性、随机性、涌现性等特点,本文从故障链角度进行事故风险研究,提出炼化装置故障链式效应定量安全预警方法,有利于全面评价故障影响下装置的整体运行风险,并及时预防故障的传播和发展。 (2)本文详细给出了炼化装置故障链式效应定量安全预警方法的具体实施步骤,具有实际指导意义。首先分析炼化装置故障链式关系结构,基于目标树成功树-动态主逻辑图(GTST-DMLD)建立其故障链式效应关系模型,揭示装置故障链式效应行为规律和关联本质,从而评价其异常工况下的安全状态。进一步以马尔可夫过程为理论基础,建立故障链式效应预测模型,预测故障传播的后果和方向,并计算各后果的发生概率,为现场操作人员进行主动维修或应急处置提供依据。 (3)案例分析中通过对某化工厂常压塔装置、减压炉装置实际发生的故障场景为研究对象,进行应用与验证,结果表明该方法可以准确地对系统故障发生后的状态进行评价和预测,方法有效、可行,便于操作人员在处置已发生故障的同时,注意预防其他异常工况的发生,降低油气生产加工过程中的整体风险。 (4)本文所述方法存在的一个局限性,便是间隔时间(Tinterval)的取值是常数,即等间隔时间的预测。未来下一步的计划将考虑研发一个模型其将会根据事态的发展实时改变预测的间隔时间(Tinterval),并有望在此方面能有所突破。 References [1] KHAN F, RATHNAYAKA S, AHMED S. Methods and models in process safety and risk management: past, present and future[J]. Process Safety and Environmental Protection, 2015, 98:116-147. [2] HU J, ZHANG L, CAI Z, et al. Fault propagation behavior study and root cause reasoning with dynamic Bayesian network based framework[J]. Process Safety and Environmental Protection, 2015, 97: 25-36. [3] GABBAR H. Improved qualitative fault propagation analysis[J]. Journal of Loss Prevention in the Process Industries, 2007, 20(3): 260-270. [4] WANG Y, CHANG C. A hierarchical approach to construct Petri nets for modeling the fault propagation mechanisms in sequential operations[J]. Computers & Chemical Engineering, 2003, 27(2): 259-280. [5] YU C, SU B. Eliminating false alarms caused by fault propagation in signal validation by sub-grouping[J]. Progress in Nuclear Energy, 2006, 48(4): 371-379. [6] GABBAR H, HUSSAIN S, HOSSEINI A. Simulation-based fault propagation analysis—application on hydrogen production plant[J]. Process Safety and Environmental Protection, 2014, 92(6): 723-731. [7] 曹雅琴, 胡瑾秋, 张来斌. 基于因果矩阵的故障链式效应时间定量模型分析方法[J]. 设备管理与维修增刊, 2015, 378:329-332. CAO Y Q, HU J Q. ZHANG L B. Fault propagation time modeling based on causal matrix [J]. Equipment Management and Repair, 2015, 378(Suppl.): 329-332. [8] HU J, YI Y. A two-level intelligent alarm management framework for process safety[J]. Safety Science, 2016, 82: 432-444. [9] ZHANG Z, WU C, ZHANG B, et al. SDG multiple fault diagnosis by real-time inverse inference[J]. Reliability Engineering & System Safety, 2005, 87:173-189. [10] LIU H, LIN Q, REN M. Fault diagnosis and cause analysis usingfuzzy evidential reasoning approach and dynamic adaptive fuzzy Petri nets[J]. Computers & Industrial Engineering, 2013, 66(4): 899-908. [11] CHENG H, HE Z, WANG Q,et al. Fault diagnosis method based on Petri nets considering service feature of information source devices[J]. Computers & Electrical Engineering, 2015, 46:1-13. [12] HU J, ZHANG L, LIANG W. Opportunistic predictive maintenance for complex multi-component systems based on DBN-HAZOP model[J]. Process Safety and Environmental Protection, 2012, 90(5):376-388. [13] CAI B, LIU Y, MA Y, et al. A framework for the reliability evaluation of grid-connected photovoltaic systems in the presence of intermittent faults[J]. Energy, 2015, 93: 1308-1320. [14] HU J, ZHANG L, MA L, et al. An integrated safety prognosis model for complex system based on dynamic Bayesian network and ant colony algorithm[J]. Expert Systems with Applications, 2011, 38(3): 1431-1446. [15] ZHAO J, CUI L, ZHAO L, et al. Learning HAZOP expert system by case-based reasoning and ontology[J]. Computers & Chemical Engineering, 2009, 33(1):371-378. [16] 李果, 高建民, 高智勇, 等. 基于小世界网络的复杂系统故障传播模型[J]. 西安交通大学学报, 2007,41(3):334-338. LI G, GAO J M, GAO Z Y, et al. Failure propagation model of complex system based on small world net[J]. Journal of Xi’an Jiaotong University, 2007,41(3):334-338. [17] LIU L, ANTONOPOULOS N, MACKIN S. Fault-tolerant peer-to-peer search on small-world networks[J]. Future Generation Computer Systems, 2007, 23(8): 921-931. [18] 吴重光, 许欣, 纳永良, 等. 基于知识本体的过程安全分析信息标准化[J]. 化工学报, 2012, 63(5):1484-1491. WU C G, XU X, NA Y L, et al. Standardized information for process hazard analysis based on ontology[J]. CIESC Journal, 2012, 63(5): 1484-1491. [19] HU Y S, MODARRES M. Evaluating system behavior through dynamic master logic diagram (DMLD) modeling[J]. Reliability Engineering & System Safety, 1999, 64(2): 241-269. [20] 郭驰名. 基于 GTST-DMLD 的系统安全性分析方法研究[D]. 长沙: 国防科技大学, 2008. GUO C M. Research on method of system safety analysis based on GTST-DMLD[D]. Changsha: National University of Defense Technology, 2008. [21] 王首臻. 基于功能模拟的装备维修规划方法研究[D]. 长沙:国防科技大学, 2006. WANG S Z. Research on the method of equipment maintenance planning based on functional modeling[D]. Changsha:National University of Defense Technology, 2006. 2015-11-26收到初稿,2016-04-01收到修改稿。 联系人及第一作者:胡瑾秋(1983—),女,博士,教授。 Received date: 2015-11-26. 中图分类号:X 937 文献标志码:A 文章编号:0438—1157(2016)07—3091—10 DOI:10.11949/j.issn.0438-1157.20151774 基金项目:国家自然科学基金项目(51574263);教育部新世纪优秀人才支持计划项目(NCET-12-0972);中国石油大学(北京)科研基金项目(2462015YQ0403)。 Corresponding author:Prof. HU Jinqiu, hujq@cup.edu.cn supported by the National Natural Science Foundation of China (51574263), the Program for New Century Excellent Talents in University(NCET-12-0972) and the Science Foundation of China University of Petroleum, Beijing (2462015YQ0403). Quantitative safety early warning method of fault propagation for petrochemical plants HU Jinqiu, ZHANG Laibin, WANG Anqi Abstract:In the petroleum system, process fault and its damage caused by the fault propagation chains have a serious effect on the oil and gas production and people's life. In this paper, from the fault causal chain perspective, a quantitative safety early warning method of fault propagation is proposed. First, the fault propagation chains is analyzed, and the GTST-DMLD (goal tree success tree, GTST; dynamic master logic diagram, DMLD) model is developed, by which the chain effect of the fault propagation behavior can be quantitatively modeled. It can be further used to evaluate the system safety state when the abnormal event happens. Based on the results of GTST-DMLD model, Markov process theory is introduced to establish a fault prognosis model, by which the fault consequence and its propagation direction can be predicted timely. The results given by the proposed method can help field operation personnel to carry out pre-active maintenance or emergency disposal. In the case study, the proposed method is applied to the atmospheric distillation unit and the vacuum furnace in a certain petrochemical company. It has been fully validated and provides a great help for the risk reduction and accident prevention in the field. Key words:process systems; goal tree success tree-dynamic master logic diagram; fault propagation; safety; prediction
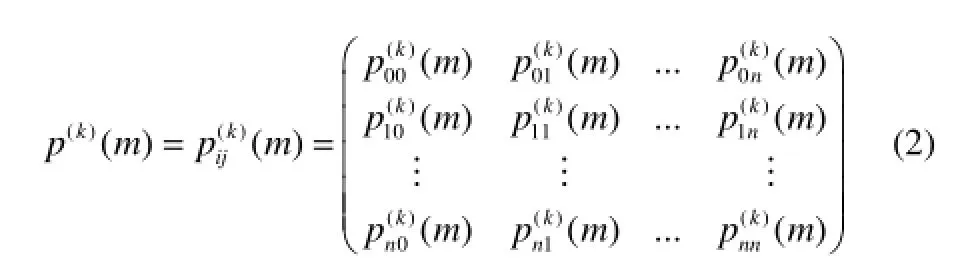
2 炼化装置故障链式效应定量安全预警方法




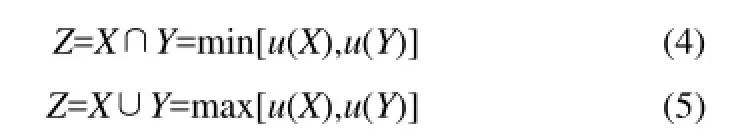




3 案例分析









3 结 论
(College of Mechanical and Transportation Engineering, Research Center of Accident Prevention and Control for Oil and Gas Industry, China University of Petroleum, Beijing 102249, China)
