基于Kern-Seaton模型结合Capdeville生物膜增长体系建立的微生物污垢模型

徐志明，沈艺雯，张一龙，刘坐东，王景涛，王宇航



基于Kern-Seaton模型结合Capdeville生物膜增长体系建立的微生物污垢模型

徐志明1，沈艺雯1，张一龙2，刘坐东1，王景涛1，王宇航1

（1东北电力大学能源与动力工程学院，吉林省 吉林市 132012；2东北电力大学自动化工程学院，吉林省 吉林市 132012）

摘要:为研究换热设备生物污垢的形成过程，将Capdeville生物膜增长体系引入Kern-Seaton模型，建立了一个新的微生物污垢模型。采用铁细菌和管式换热装置对模型进行了实验验证。结果表明:除诱导期外，新建的微生物污垢热阻模型的计算数据和实验数据的相对误差小于20%。

关键词:微生物污垢；污垢模型；Capdeville生物膜增长体系；冷却水

引 言

冷却水中常含有真菌、细菌、藻类等微生物，这些微生物及其排泄物在换热面上沉积形成微生物污垢。污垢会增加传热和流动阻力，腐蚀换热面且增加运行维护成本[1]。如何解决污垢问题成为当今传热界研究的热点问题之一。Kern等[2]建立了一个污垢热阻模型，认为污垢热阻随时间的变化是由沉积率与剥蚀率两部分叠加组成。其后大多数污垢模型都是基于这一模型发展的。但是由于微生物具有活性，从而使问题变得更为复杂。陈黎明等[3]综合考虑影响生物膜形成和稳定的多种因素，定性地分析了生物膜。基于悬浮微生物的存在，他们提出了一个生物膜的数学模型。Picioreanu等[4]利用一个二维模型对生物膜的增长进行了预测，建立了基于不同生物膜的附着、剥蚀和老化的污垢模型。Molobela等[5]则分别定量和定性地研究了微生物生物膜的生物量、结构和厚度。肖鸿等[6]通过生物膜反应器研究了生物污垢脱落的机理。Janus[7]将微生物分为可逆污垢和不可逆污垢两类，且将可逆和不可逆这两个过程以一阶常微分方程来表示，并且建立了一个集成的数学模型。Cho等[8]在生物膜反应器的背景下研究活性生物量，基于活性生物量的存在，建立了一个相关的数学模型。

Capdeville等[9]提出了生物膜增长体系这一概念，成为生物膜生长的理论依据，并基于Capdeville动力学体系在环形反应器上测试生物膜的增长，证明了体系的先进性。Roques等[10]改进了Capdeville生长体系，使体系完善。刘雨等[11]针对 Capdeville体系提出了生物膜是由降解底物的活性物质与非活性物质所组成的，系统地描述了生物膜中活性生物量与非活性生物量增长的生物数学模型体系，从理论上阐明了活性生物量与非活性生物量间动态的相互作用。虽然对这种体系有一定的研究，但是将体系引入换热设备微生物污垢方面的研究还未见报道，本文将 Capdeville动力学体系引入Kern-Seaton模型，建立了一个新的换热设备微生物污垢模型。

1　微生物污垢模型

污垢的形成过程是质量交换、热量交换和动量交换的动态综合，是十分复杂的过程。微生物污垢在起始阶段，黏膜生长很慢，这是因为宏观分子附着前需对表面做必要的调适。接着黏膜呈指数增长，黏膜趋近稳态厚度。生物污垢的形成一般都要经历以下5个阶段:起始、输运、附着、剥蚀和老化。这些阶段，可以依序连续发生，也可以同时发生[1]。

这个过程可以采用Kern-Seaton模型[1]描述

式中，Φd为沉积率，m·K·N-1；Φr为剥蚀率，m·K·N-1；Rf为微生物污垢的污垢热阻，m2·K·W-1；t为时间，h。

1.1 微生物污垢的沉积率

这里借用Capdeville生物膜增长体系构建生物污垢的沉积率。

微生物随着流体流动，一部分会悬浮在流体中，一部分则会附着在换热面上形成污垢。沉积在表面上的微生物仍具有活性，会继续繁殖、增长。污垢层中微生物的增长过程一般认为与悬浮微生物的增长过程相似[12]。

Capdeville按照生物活性将微生物污垢中的生物量分为两类:活性生物量（Ma），代表具有活性并且在适宜的生长环境下可以生长、繁殖的部分，它处于新生菌落及已经存在菌落的表面和边缘部分；非活性生物量（Mi），代表在底物降解过程中不再起任何作用的生物膜量，这些非活性生物量主要集中在菌落内部[13]。

由上分析可以认为微生物污垢的沉积率由活性生物量累积率和非活性生物量累积率两部分组成，即

式中，rMa为活性生物量累积率，m·K·N-1；rMi为非活性生物量累积率，m·K·N-1。

活性生物量累积率的增长主要发生在生物膜动力学增长期，表现为线性增长[14]，即活性生物量的一级反应动力学为

式中，μ0为最大比增长率，与温度有关，一般取值在0.06～0.5之间[13]；Ma为活性生物量。

非活性生物量的增长则取决于生物膜自身活性生物量以及抑制性物质的浓度，即

其中抑制性产物浓度为

式中，k1为生物失活性系数；αi为常数。

将式(5)代入式(4)，得非活性生物量累积率的表达式，即

式中，k2= k1αi，与微生物种类和工质的工况有关。

因为活性生物量与微生物浓度应呈比例，即

式中，k3为活性生物量与微生物浓度的比例系数，受微生物所生存的流体流速、温度等工况影响。所以再将活性生物量累积率式(3)和非活性生物量累积率式(6)、式(7)一同代入式(2)，可得沉积率模型，即

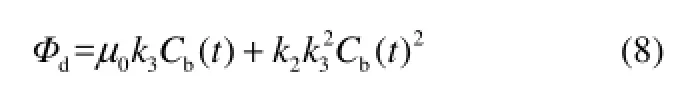
1.2 微生物污垢的剥蚀率

对于剥蚀率Φr，根据Taborek 等[15]或Gudmundson[16]的建议，取通用污垢剥蚀率模型

式中，k4为剥蚀率的系数，会随着流体流速、温度等工况的改变而改变。

不同α值适应不同污垢沉积率模型，对应于颗粒污垢、析晶污垢和微生物污垢均适用。当α=0时，适用于颗粒污垢。而α=0.54，适用于析晶污垢[17]。由于微生物污垢的强度介于颗粒污垢与析晶污垢之间，所以微生物污垢中，0< α<0.54。根据计算发现α数值的变化对结果影响较小，最终根据污垢热阻实验选定α=0.44。

1.3 微生物污垢的热阻模型

将沉积率式(8)和剥蚀率式(9)代入 Kern-Seaton模型式(1)，得到

积分式(10)，得微生物污垢热阻表达式

1.4 微生物生长动力学模型

微生物的生长动力学模型是表征微生物浓度Cb(t)与时间t的关系，即微生物的响应。而Cb(t)为污垢热阻表达式中的重要参数。本文采用Boltzmann方程来表征微生物浓度

式中，t是时间，h；A1是相对最小值；A2是相对最大值；t0是对应的(A1-A2)/2的时刻，h；tm为大于0的参数。

将Cb(t)代入式(11)，为方便求解，将式(11)分解为两个相似部分，继续化简求解。其中，分别有一部分不能直接积分，即

于是采用泰勒公式中的麦克劳林方法将式(13)和式(14)分别化简、积分，得

并代回式(11)得

式中各个常数都是假定值。实验研究[18-20]表明，一般微生物污垢热阻都是渐近式，如果各个常数之间满足下面关系

则污垢热阻即为渐近型

2　实验验证

为了验证所建立的微生物污垢热阻模型的正确性，本文采用文献[21]中的实验装置，获取参数并进行实验验证。采用在线监测系统采集污垢热阻数据。实验工质选择铁细菌，实验所采用的铁细菌为国内某电厂循环冷却塔塔底黏泥中分离纯化出的。实验系统具体参数见文献[21]。圆管恒温水浴加热管内湍流流体，实验中选择将铁细菌菌液和去离子水按比例 1:100均匀混合后作为循环流动工质，圆管内径d = 22 mm，管长L = 2200 mm。其他物性参数均取300 K水的物性参数。边界条件为恒壁温50℃。

实验过程中，采用平板菌落计数法对水质中的铁细菌菌落数进行查数，本组实验工况选定入口温度为35℃，得到数据见表1。

表1　细菌菌落数Table 1 Numbers of bacterial colonies

将表1数据代入式(12)，即得到拟合的微生物铁细菌的生长动力学方程

其中常数对应为:A1=-119593，A2=3.1×108，t0=50.2，tm=6.41。

对于入口温度为30℃，流速为0.4 m·s-1的工况，根据实验取k2=0.50，根据文献[13]取μ0=0.22，在已知这两个参数的基础上，结合式(18)和渐近污垢热阻值两个公式可以求出k3、k4两个参数，如表2所示。

表3　Tfi= 30℃的微生物污垢模型中参数Table 2 Parameters in microbial fouling model when Tfi= 30℃

将上述所需的参数代入污垢热阻模型式(19)中，得到入口温度为30℃的污垢热阻实验值和污垢热阻模型计算值的对比如图1所示，对应的相对误差如图2所示。从图2可以看出，除诱导期外，不锈钢光管内铁细菌微生物污垢的计算值与实验值的相对误差都在±20%以内。由于建模过程没有考虑污垢形成过程对传热的影响，所以诱导期部分吻合效果不好。

在保证入口温度为 30℃的前提下，将流速由0.4 m·s-1变为0.3 m·s-1，此时得到的污垢热阻实验值和污垢热阻模型计算值对比如图3所示，对应的相对误差如图4所示。

图1　30℃的计算值与实验值对比Fig.1 Comparison between calculated values and experimental values when Tfi= 30℃

图2　30℃的计算值与实验值的相对误差Fig.2 Relative error between calculated values and experimental values when Tfi= 30℃

图3　0.3 m·s-1的计算值与实验值对比Fig.3 Comparison between calculated values and experimental values when v= 0.3 m·s-1

图4　0.3 m·s-1的计算值与实验值的相对误差Fig.4 Relative error between calculated values and experimental values when v= 0.3 m·s-1

由图4可以得到，除了诱导期外，污垢的计算值与实验值的相对误差都在±20%以内。对应的微生物污垢模型中的参数如表3所示。

表3　v= 0.3 m·s-1的微生物污垢模型中参数Table 3 Parameters in microbial fouling model when v= 0.3 m·s-1

3　结 论

将Capdeville生物膜增长体系引入Kern-Seaton模型，所建立的微生物污垢模型与实验结果的相对误差除诱导期外均小于20%。

符 号 说 明

A1,A2——分别为微生物生长动力学方程中的相对最大值和相对最小值

Cb(t) ——微生物浓度，CFU·L-1

Ci——抑制性产物浓度，CFU·L-1

d ——管式换热器的不锈钢光管内径，mm

I1,I2——分别为微生物污垢热阻模型的一部分

k1,k2,k3——生物沉积率模型中的常参数

k4——生物剥蚀率模型中的常参数

L ——管式换热器的不锈钢光管长度，mm

Ma——活性生物量

Mi——非活性生物量

Rf——微生物污垢的污垢热阻，m2·K·W-1

Rf

*——微生物污垢的渐近污垢热阻值，m2·K·W-1

rMa——活性生物量累积率，m·K·N-1

rMi——非活性生物量累积率，m·K·N-1

t ——时间，h

tc,t0——渐近式微生物污垢热阻模型中的时间参数，h

tm——微生物生长动力学方程中关于时间的参数，h

v ——实验中流体流速，m·s-1

α ——剥蚀率模型中的指数参数

αi——常参数

μ0——最大比增长率

Φd——沉积率，m·K·N-1

Φr——剥蚀率，m·K·N-1

References

[1] 杨善让, 徐志明, 孙灵芳. 换热设备污垢与对策[M]. 北京: 科学出版社, 2004: 1-76.

YANG S R, XU Z M, SUN L F. Fouling and Countermeasures for Heat Transfer Equipment[M]. Beijing:Science Press, 2004: 1-76.

[2] KERN D Q, SEATON R E. A theoretical analysis of thermal surface fouling[J]. Chem. Eng. Prog., 1959, 4(5): 258-262.

[3] 陈黎明, 柴立和. 生物膜废水处理系统的数学模型及机理探讨[J].自然科学进展, 2005, 15(7): 843-848.

CHEN L M, CHAI L H. Mathematical model and mechanism of biofilm wastewater treatment system[J]. Progress in Natural Science, 2005, 15(7): 843-848.

[4] PICIOREANU C, LOOSDRECHT M C V, HEIJNEN J J. Two-dimensional model of biofilm detachment caused by internal stress from liquid flow[J]. Biotechnology & Bioengineering, 2001, 72(2): 205-218.

[5] MOLOBELA I P, ILUNGA F M. Impact of bacterial biofilms: the importance of quantitative biofilm studies[J]. Annals of Microbiology, 2012, 62(2): 461-467.

[6] 肖鸿, 杨平, 郭勇, 等. 生物膜反应器中生物膜脱落的机理及数学模型[J]. 化工环保, 2005, 25(1): 23-28.

XIAO H, YANG P, GUO Y, et al. Biofilm detachment mechanism and mathematical models[J]. Environmental Protection of Chemical Industry, 2005, 25(1): 23-28.

[7] JANUS T. Integrated mathematical model of a MBR reactor including biopolymer kinetics and membrane fouling[J]. Procedia Engineering, 2014, 70: 882-891.

[8] CHO J, AHN K H, SEO Y, et al. Modification of ASM No.1 for a submerged membrane bioreactor system: including the effects of soluble microbial products on membrane fouling [J]. Water Science & Technology, 2003, 47(12): 177-181.

[9] LIU Y, CAPDEVILLE B. Dynamics of nitrifying biofilm growth in biological nitrogen removal process[J]. Waterence & Technology, 1994, 29(7): 377-380.

[10] ROQUES H, YUE S, SAIPANICH S, et al. Faut-il abandonner le formalisme de monod pour la modelisation des processus de depollution par voie biologique?[J]. Water Research, 1982, 16(6): 839-847.

[11] 刘雨, 王岐东. 生物膜增长动力学模型[J]. 北京轻工业学院学报, 1997, 15(2): 28-31.

LIU Y, WANG Q D. Kinetic models of biofilm growth[J]. Journal of Institute of Light Industry, 1997, 15(2): 28-31.

[12] 曾庆楠, 吴云, 张宏伟, 等. 膜材料对膜曝气生物膜反应器性能影响的比较[J]. 化工学报, 2016, 67(4): 1483-1489.

ZENG Q N, WU Y, ZHANG H W, et al. Effects of membrane materials on the performance of membrane aerated biofilm reactor[J]. CIESC Journal, 2016, 67(4): 1483-1489.

[13] 刘雨. 生物膜法污水处理技术[M].北京: 中国建筑工业出版社, 2000: 47-58.

LIU Y. Sewage Disposal Technology of Biofilm Process[M]. Beijing: China Architecture & Building Press, 2000: 47-58.

[14] 陈胜, 孙德智, 陈桂霞, 等. 移动床生物膜法处理垃圾渗滤液COD降解动力学[J]. 化工学报, 2007, 58(3): 733-738.

CHEN S, SUN D Z, CHEN G X, et al. Kinetics of COD degradation in landfill leachate treatment using moving bed bioreactor[J]. Journal of Chemical Industry and Engineering(China), 2007, 58(3): 733-738.

[15] TABOREK J, AOKI T, RITTER R B, et al. Fouling: the major unresolved problem in heat transfer[J]. Chem. Eng. Prog., 1972, 68(2): 59-68.

[16] GUDMUNDSON J. Heat transfer fouling[D]. Birmingham: University of Birmingham, 1977.

[17] 徐志明, 张一龙, 徐欣. 温度及浓度对析晶污垢沉积特性影响的模拟研究[J]. 中国电机工程学报, 2014, 34(35): 6263-6270. DOI: 10.13334/j.0258-8013.pcsee.2014.35.002.

XU Z M, ZHANG Y L, XU X. Simulation study on influent of temperature and concentration on crystallization fouling deposition[J]. Proceedings of the CSEE, 2014, 34(35): 6263-6270. DOI: 10.13334/j.0258-8013.pcsee.2014.35.002.

[18] 于大禹, 尹旭, 张静, 等. 基于模拟循环冷却装置的微生物污垢形成的影响因素[J]. 化工学报, 2011, 62(12): 3503-3510. DOI: 10.3969/j.issn.0438-1157.2011.12.030.

YU D Y, YIN X, ZHANG J, et al. Factors affecting microbial fouling formation in simulated recirculating cooling-water system[J]. CIESC Journal, 2011, 62(12): 3503-3510. DOI: 10.3969/j.issn.0438-1157. 2011.12.030.

[19] 田磊, 杨倩鹏, 史琳, 等. 热泵工况下竖直不锈钢表面微生物污垢动态生长行为[J]. 化工学报, 2012, 63(1): 230-236. DOI: 10.3969/j.issn.0438-1157.2012.01.032.

TIAN L, YANG Q P, SHI L, et al. Evolution of biofouling on a vertical stainless steel surface caused by bacillus subtilis under heat pump conditions[J]. CIESC Journal, 2012, 63(1): 230-236. DOI: 10.3969/j.issn.0438-1157.2012.01.032.

[20] 关晓辉, 崔长龙, 曹生现, 等. 不锈钢缩放管中典型致垢微生物致垢能力[J]. 化工进展, 2013, 32(6): 1429-1434. DOI: 10.3969/ j.issn.1000-6613.2013.06.038.

GUAN X H, CUI C L, CAO S X, et al. Study on fouling ability of typical fouling microorganisms in the stainless steel zoom pipe[J]. Chemical Industry and Engineering Program, 2013, 32(6): 1429-1434. DOI: 10.3969/j.issn.1000-6613.2013.06.038.

[21] 徐志明, 郝占龙, 张一龙, 等. 交叉缩放椭圆管中微生物污垢特性[J]. 微生物学通报, 2013, 40(11): 1978-1986. DOI: 10.13344/ j.microbiol.china. 2013.11.002.

XU Z M, HAO Z L, ZHANG Y L, et al. Microbial fouling characteristics of the alternating elliptical axis tube[J]. Microbiology China, 2013, 40(11): 1978-1986. DOI: 10.13344/j.microbiol.china. 2013.11.002.

2015-12-21收到初稿, 2016-04-26收到修改稿。

联系人:沈艺雯。第一作者:徐志明（1959—），男，博士，教授。

Received date: 2015-12-21.

中图分类号:TK 124

文献标志码:A

文章编号:0438—1157（2016）07—2998—06

DOI:10.11949/j.issn.0438-1157.20151944

基金项目:国家自然科学基金项目（51476025）。

Corresponding author:SHEN Yiwen,syw2009zhf@sina.com supported by the National Natural Science Foundation of China (51476025).

A microbial fouling model based on Kern-Seaton model and Capdeville biofilm growth system

XU Zhiming1, SHEN Yiwen1, ZHANG Yilong2, LIU Zuodong1, WANG Jingtao1, WANG Yuhang1
(1School of Energy and Power Engineering, Northeast Dianli University, Jilin 132012, Jilin, China;2School of Automation Engineering, Northeast Dianli University, Jilin 132012, Jilin, China)

Abstract:In order to study biofouling process in heat exchangers, a new microbial fouling model was established by introducing the Capdeville biofilm growth system into the Kern-Seaton model. The new model was verified by experiments of the iron bacteria growth in tubular heat exchangers. Less than 20% relative error was achieved between the model prediction and the experimental data regardless of the induction period.

Key words:microbial fouling; fouling model; Capdeville biofilm growth system; cooling water