投影与视图新题型
2016-08-05文/丁洁
文/丁 洁
投影与视图新题型
文/丁洁

投影和视图是空间与图形的重要内容,也是中考新题型的好素材.投影与视图的新题型主要有:
一、开放发散型
例1(2014年汕尾卷)写出一个在三视图中俯视图与主视图完全相同的几何体.
解析:球的俯视图与主视图都为圆,正方体的俯视图与主视图都为正方形,答案可以从球或正方体中任意选一个.
温馨小提示:熟悉三视图的概念和常见几何体的三视图是解题的前提.
二、方案设计型
例2(2015年佛山卷)如图1,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方案.
解析:(1)在Rt△ABC中,由AC=5.5,∠C=37°,得AB=AC·tan C=5.5×0.75≈4.1(米). (2)从边和角两方面考虑,可得两种方案:①增加路灯D的高度;②使路灯D向墙靠近.温馨小提示:理解三角函数概念,掌握三角函数与直角三角形的边角关系是解题的关键.

图1
三、视图变化型
例3(2015年菏泽卷)图2是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体().
A.主视图改变,左视图改变B.俯视图不变,左视图不变
C.俯视图改变,左视图改变D.主视图改变,左视图不变
解析:比较移动前与移动后三种视图,立可得到答案,选D.
温馨小提示:分别标出移动前后三视图的正方形的列数及每列正方形的个数是解题的关键.

图2
四、知识渗透型
例4(2014年巴中卷)如图3,两个大小不同的实心球在水平面靠在一起,则该几何体的左视图是().
A.两个外切的圆B.两个内切的圆
C.两个内含的圆D.一个圆
解析:左视图是两个内切的圆,切点在水平面上.选B.
温馨小提示:从左面看,两个圆有一个公共点,且小圆在大圆的内部.本题将两圆位置关系的判定与三视图的识别有机综合,十分巧妙自然.
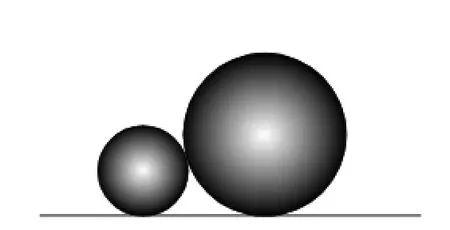
图3
五、定量计算型
例4(2015年玉林卷)图4是七个棱长为1的正方体组成的一个几何体,其俯视图的面积是().
A.3B.4
C.5D.6
解析:由图4及正方体的个数可知俯视图有五个正方形,如图5,它的面积为5.选C.
温馨小提示:将三视图的判定转化为简单图形面积的计算,命题形式新颖.

图4
六、整体思考型

图5
例6 (2014年枣庄卷)从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图6所示的零件,则这个零件的表面积是________.
解析:观察正方体毛坯,发现挖去一个棱长为1的小正方体,这个零件的表面积仍等于原正方体的表面积.因为正方体的棱长为2,所以正方体的表面积为6×22=24.填24.
温馨小提示:常规解法是把每个面的面积计算出来相加,这样做比较麻烦.从整体思考,利用平移补形,解法十分简捷.
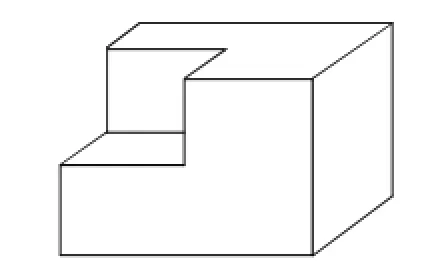
图6
七、几何体拼组型
例7(2015年青岛卷)如图7,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使两个几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要________个小正方体,王亮所搭几何体的表面积为________.
解析:大长方体至少需要小立方体4×32=36个.
∴王亮至少还需36-17=19个小立方体,表面积为2×(9+7+8)=48,
故分别填19,48.
温馨小提示:确定两人所搭几何体的形状是解题的关键.
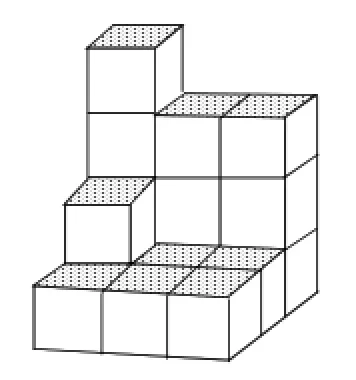
图7
八、方程应用型
例8(2015年镇江卷)某兴趣小组开展课外活动.如图8,A、B两点相距12米,小明从点A出发,沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C、E、G在一条直线上).
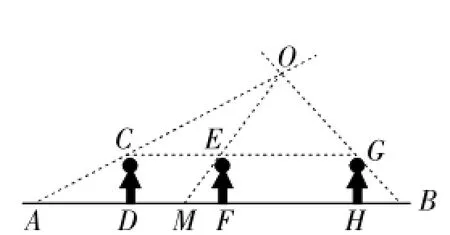
图8
(1)请在图中画出光源O点的位置,并画出他位于点F时的影长FM(不写画法);
(2)求小明原来的速度.
解析:(1)如图8,点O为光源,FM为影长.
(2)∵点C、E、G在一条直线上,CG∥AB,
经检验,v=1.5是方程的根.
小明原来的速度为1.5m/s.
温馨小提示:影长问题,要弄清是平行投影还是中心投影下的影长,应用相似三角形的知识来解决.
责任编辑:王二喜
