从余弦定理的证明看学生的发散思维

郭俊楠

河南师范大学数学与信息科学学院，河南　新乡　453007



从余弦定理的证明看学生的发散思维

郭俊楠

河南师范大学数学与信息科学学院，河南新乡453007

摘要：纵观近几年的数学高考试卷，我们发现对学生发散思维的考察越来越多，但学生具有较好的思维发散能力并不仅仅是数学的要求。在当今这个飞速发展的信息化时代，求异和创新愈发显得弥足珍贵。所以，学生发散思维的培养和锻炼一直是现代教学中的重点与难点。本文从余弦定理的证明出发，多方面、多层次地进行思考和分析，在探讨多样证明方法的同时，以寻求培养学生发散思维的策略。

关键词：余弦定理；发散思维；求异；创新

何为发散思维？根据思维的指向性，思维可分为集中思维和发散思维。思维是人脑对客观现实概括的和间接的反映，它体现的是事物的本质与内部规律性。发散思维也称辐散思维、求异思维，是根据已有的信息，从不同角度思考，从多方面寻求多样性答案的一种展开性思维活动。下面，我们就从余弦定理的多种证法看学生思维的发散性。

在数学中，用符号语言来描述余弦定理，即：a2=b2+c2-2bccosA ① b2=a2+c2-2accosB②c2=a2+b2-2abcos③

分析：余弦定理的公式中给出了四个量，“知三可求一”，因此，证明余弦定理即解决已知其中的三个量来表示另外一个量的问题。

思维取向一：解析法

在△ABC上建立直角坐标系，如图1，点A为原点，点B落在x轴正半轴上，设三角形 三边分别为a,b,c,则三点的坐标分别为A(0,0),B(c,0),C(bcosA,bsinA),已知BC=a,由两点间距离公式可得：

化简可得：a2=b2+c2-2bcosA

同理可得②③.

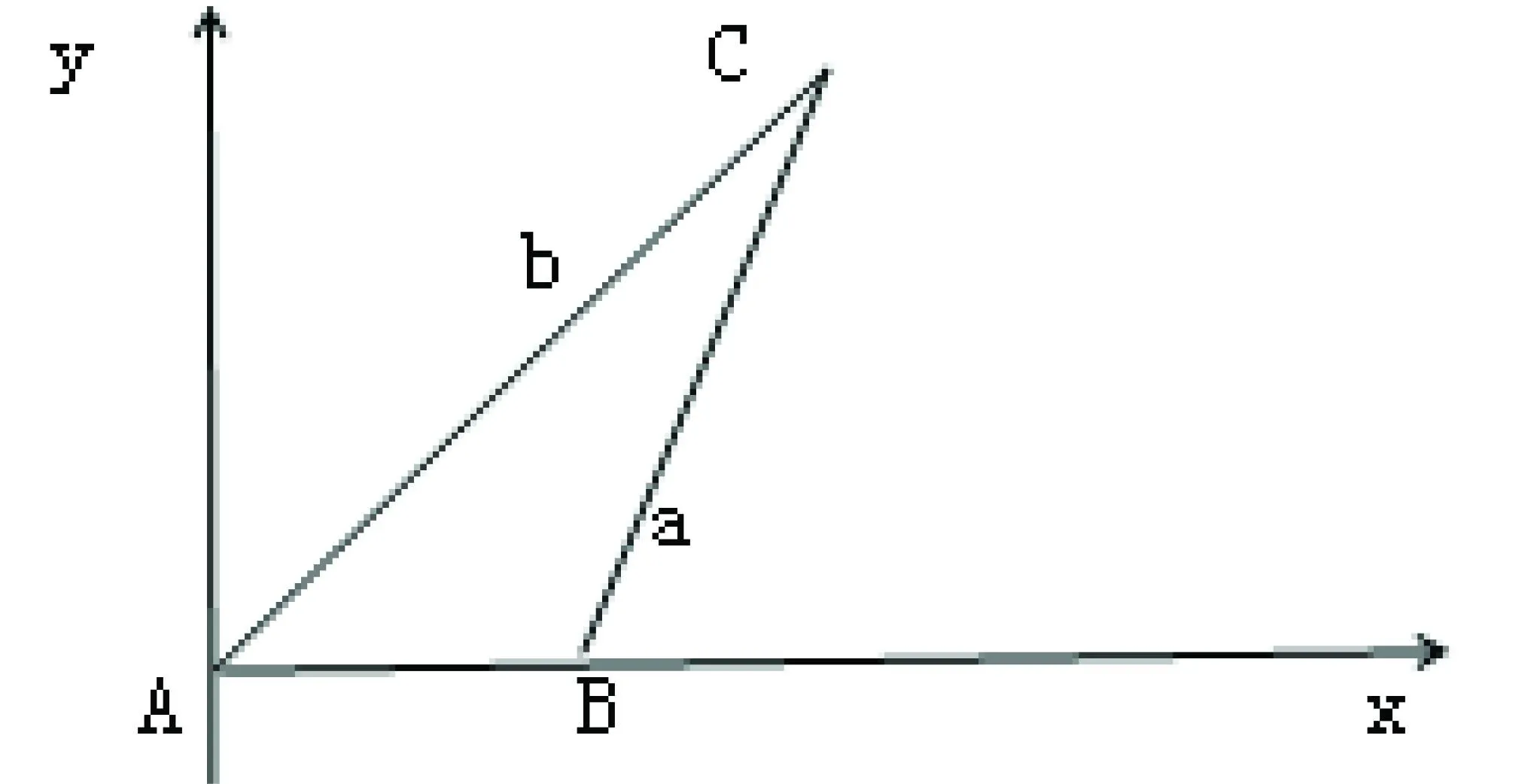
图1

点评：此法是通过建立坐标系将几何问题用代数观点来解决。笔者认为这个方法简单易懂，学生很容易就能想到求边长也即求两点间的距离，关键是要想到如何巧妙地建立直角坐标系(将一点放在原点，另一点置于x轴上)。

思维取向二：勾股法

在任意△ABC中，如图2，AB=c,AC=b,BC=a过点A作边BC的高AD,则由图2可知 AD=cinB,CD=a-ccosB

在RT△ADC中，满足AC2=AD2+DC2

b2=c2sin2B+a2+c2cos2B-2accosB

=c2+a2-2accosB

同理可得②③.

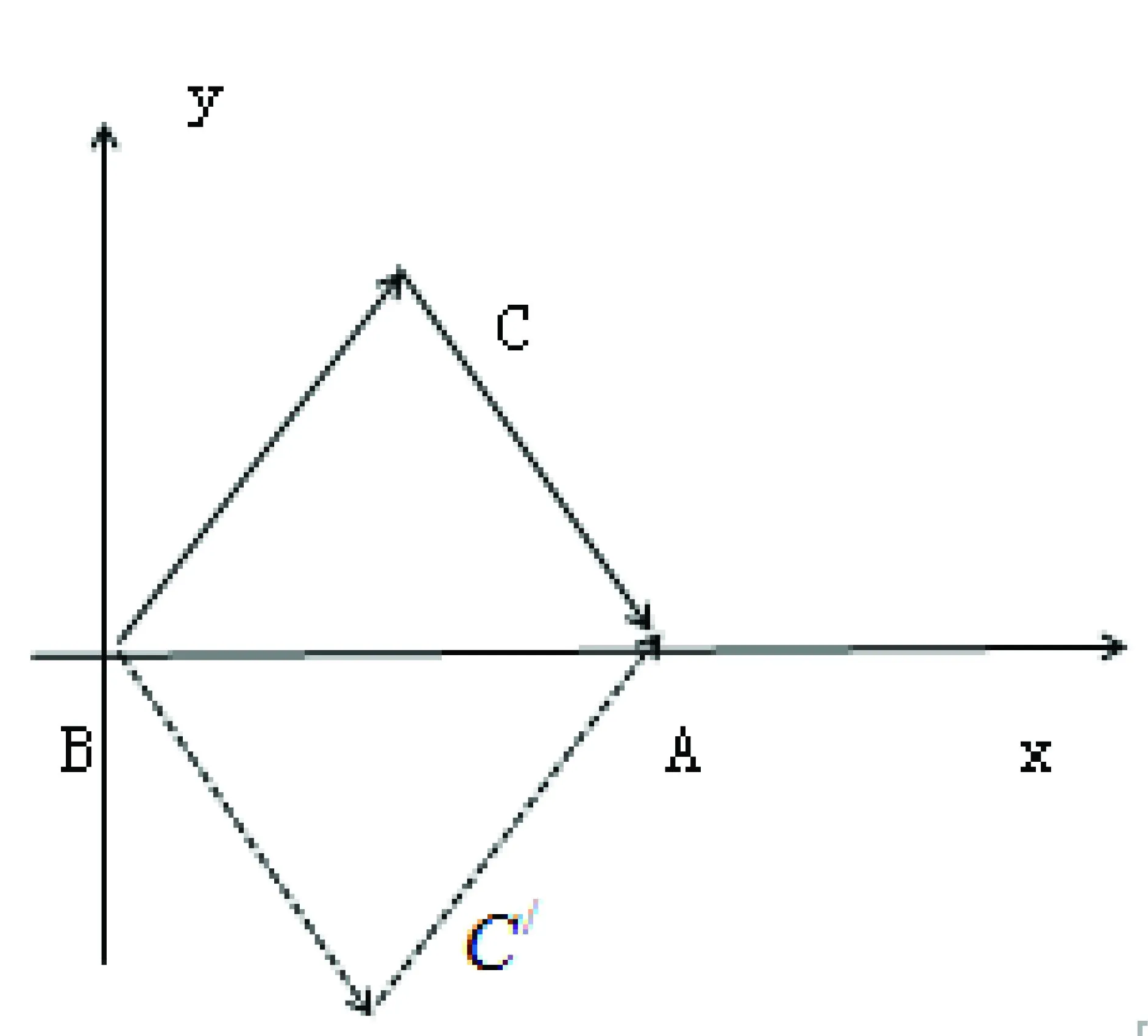
图2

点评：笔者认为此方法相对前三种方法不管是在计算量上还是思路上都更为简单。一开始我们接触到的锐角三角函数是根据直角三角形中的锐角得到的，而余弦定理是适用于任意三角形，通过在任意三角形中构造直角三角形，恰当地运用三角函数将边角关系有机的结合起来，即可得到余弦定理，其实，我们不难发现当一个角为直角时余弦定理即为勾股定理。

思维取向三：射影定理法

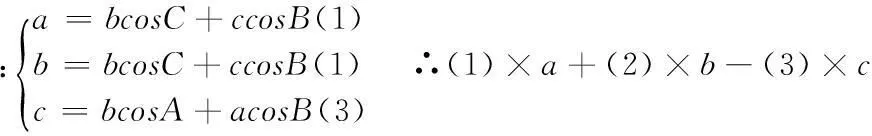
即c2=a2+b2-2abcosC

同理可得②③.

分析：余弦定理刻画的是任意三角形边角的关系，任意三角形的射影定理也涉及到边长和角度，为了将两者联系起来进行了步骤＊，稍加整理即可得到余弦定理。

思维取向四：复数法

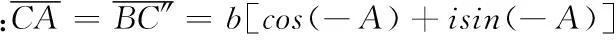
即：c=a(cosB+isinB)+b(cosA-isinA)=(acosB+BcosA)+i(asinB-bsinA)(*)

对等式(*)两边分别平方可得：c2=a2+b2-2abcosC，同理可得②③.

点评：此方法是上述向量法与解析几何法的结合，不同之处在于此方法中的坐标系与计算均是在复数领域内。

这四种证法对于高中生来说并不难理解，在学生原有的认知结构为基础之上，通过将新旧知识间建立联系。但难的是如何针对一个问题从不同角度找到多样的解决办法。这就需要现代教师在教学过程中有意识地培养学生的发散性思维。

通过对余弦定理证法的思考与分析，并结合思维的一般品质，关于如何培养学生的发散思维我提出以下三点。首先应引导学生在学习中抓住事物的规律和本质，深入的思考问题，从而增加学生思维的深刻性，为思维的发散奠定一个良好的基础。其次，鼓励学生在学习中追求“标新立异”，勇于创新。因此，在教学过程中，可以根据学生的这种心理特点，鼓励其大胆想象，尝试突破思维的局限，从多角度、多层面思考问题。如复数法或许就很少同学能够想到，因为大家都不约而同地将余弦定理限定在实数范围，很少去想利用复数能不能解决这个问题；大多数同学也都认为用数学知识解决物理问题理所当然，而不会想到是否可以用物理知识解决数学问题。同时，作为教师应用包容与鼓励的眼光看待学生在“求异”过程中出现的错误与失败，并以恰当的方式帮助学生改正想法中的不足。当然，适当的有针对性的习题训练对学生发散思维的培养也是必要的。结合教学内容和学生实际情况，采取多种形式的习题训练，可激发学生求异创新的欲望，帮助学生养成多角度思考问题的习惯。

[参考文献]

[1]孔凡哲，曾峥编著.数学学习心理学[M].第2版.北京：北京大学出版社，2012,5:197-203.

[2]徐英.用物理法证明正弦定理与余弦定理[J].中学数学杂志，2006.9.

[3]杨春茹.高中数学教学中培养学生发散思维的研究与实践[D].中国知网数据库.东北师范大学,2003.5.

[4]方炫苏，方华平.余弦定理的几个证明方法[J].中学生数学，2013.5.

中图分类号：G633.6

文献标识码：A

文章编号：1006-0049-(2016)14-0194-01