高职物理教学多元智能评价体系与评价方法研究

梁金荣，许庆兵

高职物理教学多元智能评价体系与评价方法研究

梁金荣，许庆兵

（滁州职业技术学院，安徽 滁州 239000）

高职物理教学评价中可采用多元智能理论应用到，用模糊综合评判法建立高职物理教学的多元智能评价模型。

高职物理；多元智能；评价；模型

传统的智能理论认为，智能是以语言能力和数理逻辑能力为核心的并以整合的方式存在的一种能力［1］。进入20世纪80年代，这种智能理论开始受到不少心理学家的批评与质疑，1983年美国哈佛大学心理学教授霍华德·加德纳博士在其著作《智能的结构》中提出了多元智能理论。它指出了人类的智能是多元的，主要由语言智能、数理逻辑智能、视觉空间智能、身体运动智能、音乐智能、自然观察智能、人际交往智能、自知自省智能八项组成［2］。该理论一经提出，引起了全世界教育家的广泛关注。特别是近20年，“多元智能”理论对传统的“一元智能”观提出了挑战，在各科教育理论，特别是教育评价理论上，也掀起研究热潮。

本文根据已有的研究基础，将多元智能理论应用到高职物理教学评价中，首先考虑和集成综合高职物理教学评价过程中的各种多元智能的定性与定量信息，采用层次分析法赋权，然后用模糊综合评判法建立高职物理教学的多元智能评价模型。期望能为高职物理教学水平高低的快速评价提供理论依据，为高职物理教学质量的监管起到一定的决策辅助作用。

一、高职物理教学多元智能评价指标体系的构建

物理学是一门自然科学，需要利用数学知识对问题进行定量研究。高职物理教学多元智能评价是一个多层次、多属性的决策问题，我们以科学性、全面性、层次性及可操作性为原则，根据物理课程标准和多元智能理论，结合相关专家的教学管理经验，建立包含知识与技能、过程与方法以及情感态度与价值观三个一级指标在内的高职物理教学多元智能评价指标体系，如表1。

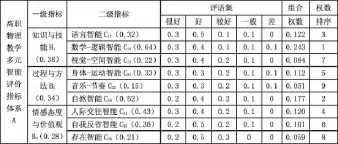
表1　高职物理教学多元智能评价指标体系及指标权重与排序表

（一）知识与技能包含语言智能、数学-逻辑智能以及视觉-空间智能3个二级指标。其中语言智能主要考察学生能否科学、恰当地描述物理现象、概念以及物理过程与经历，能否顺利阅读教材、物理问题，并正确理解；数学-逻辑智能主要考察学生能否对物理问题进行定量和定性分析，能否对物理问题进行数学模型构建，并用恰当的数学表达；视觉-空间智能主要考察学生能否形成正确物理表象，并将之形象化表达，能否画出知识结构和问题求解流程图。

（二）过程与方法包含身体-运动智能、音乐-节奏以及自然智能。其中身体-运动智能主要考察学生能否熟练操作实验仪器，能积极参与并按要求进行模拟演示；音乐-节奏主要考察学生能否进行规律性信号与噪音之间的辨别；自然智能主要考察学生是否善于并喜好从身边生活中观察常见自然现象，乐于探究，并善于在实验中发现异常现象。

（三）情感态度与价值观包含人际交往智能、自我反省智能以及存在智能。其中人际交往智能主要考察学生是否愿意参加问题讨论，并分享成果与感受，能否与同学一起合作完成学习或探究任务，能否欣赏他人，并善于学习他人优点；自我反省智能主要考察学生能否及时反思实验方案或技能操作中的步骤，能否自己确立个人学习目标并及时反馈总结，能否在物理知识学习的基础上，反思自己和他人的行为对环境的影响；存在智能主要考察学生能否将物理学知识与实际生活、社会发展、环境保护等问题联系起来。

二、高职物理教学多元智能评价模型的建立

（一）评价要素指标体系的设置。本文建立的评价要素指标体系如表1所示。

（二）评语级的确定。根据评价决策的实际需要，将评价等级标准分为“很好”、“好”、“较好”、“一般”和“差”五个等级，即评语集合为V=｛ν1，ν2，ν3，ν4，ν5｝=｛很好，好，较好，一般，差｝，对其赋值则V= ｛95，85，75，65，55｝。

（三）权重的确定。用层次分析法确定权重的基本步骤为：

1、建立层次结构模型，如表1所示。

2、构造成对比较阵。从层次结构模型的第二层开始，对于从属于或影响及上一层的每个因素的同一层诸因素，用成对比较法和1-9比较尺度（表2）构造成对比较阵，直到最下层。

表2　1-9尺度αij的含义

3、计算权向量并做一致性检验。对于每一个成对比较阵，计算最大特征根及对应的特征向量，利用一致性指标，随机一致性指标和一致性比率做一致性检验。若检验通过，特征向量（归一化后）即为权向量，若不通过，需要重新构造成对比较阵。

4、计算组合权向量并作组合一致性检验［3］。

（四）模糊综合评判。首先，由评判专家小组（n人）根据已确定的评价等级标准依次对各指标进行评价，然后统计出评为ν1（很好）、ν2（好）、ν3（较好）、ν4（一般）、ν5（差）等级的人数n1、n2、n3、n4、n5，其中n=进行归一化后得该单因素的隶属度（n1/n， n2/n，n3/n，n4/n，n5/n），这样可分别得到各子集Ci（i=1，2，3，4）中单要素的评价决策矩阵 ，然后根据文献［4］中的多级综合评判方法依次求得各子集评价决策矩阵，并最终求得高职物理教学多元智能水平评价结果。

三、实例应用

（一）各级指标权重的确定

1、分析各影响因素，建立层次结构模型。评价指标体系，见表1。

2、构造成对比较阵。建立层次结构模型后，上下层之间元素的隶属关系就被确定了。以上一层（目标层）的元素A为准则，对下一层（准则层）的元素B1、B2、B3有支配关系，对于准则A，首先要确定同层元素Bi和Bj哪一个更重要，重要多少，一般用相对重要度表示，构造A-B成对比较阵MA-B，再用同样的方法建立子准则层对准则层的成对比较阵MB1-C，MB2-C，MB3-C。这里以一级指标知识与技能（B1）的3个二级指标为例，说明权重的确定过程。

3、计算权向量并做一致性检验。对于每一个成对比较阵MB1-C，用和法［3］计算最大特征根及对应的特征向量（需归一化），并做一致性检验的结果为：权重wB1-C=（0.32，0.64，0.22），λ=3.002，CI=0.01，RI=0.58，CR=0.002＜0.1通过一致性检验，故wB1-C的三个分量就是三个二级指标语言智能（C11）、数学-逻辑智能（C12）、视觉-空间智能（C13）对一级指标知识与技能（B1）的权重。同理，可求得其余各级权重，wB2-C=（0.33，0.15，0.52），wB3-C=（0.43，0.36，0.21），wA-B=（0.38，0.34，0.28），即表1括号中的数值。

4、计算组合权数。将一级指标权重与二级指标权重相乘即得各因素对高职物理教学多元智能水平影响的综合权重，见表1。

（二）综合评判的实施

对于知识与技能的评判矩阵

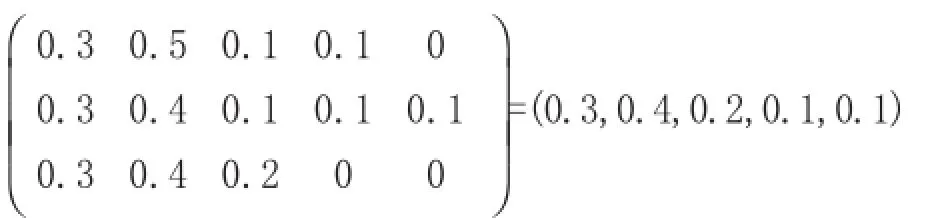
经归一化处理得：B1=（0.273，0.364，0.182，0.091，0.091），同理可得，对过程与方法、情感态度与价值观的综合评判结果为

B2=（0.250，0.333，0.250，0.083，0.083），

B3=（0.297，0.396，0.208，0.099，0），

最后，得到对该高职物理教学多元智能水平的综合评判

经归一化处理得：

B=（0.258，0.336，0.231，0.091，0.084）

（三）评价得分，由公式Z=B·VT，得到该高职物理教学多元智能水平的最终综合评价得分为Z= （0.258，0.336，0.231，0.091，0.084）· （95，85，75，65，55）T=80.93。

（四）结论分析

1、由上述计算可知，该高职物理教学多元智能水平“很好”的隶属度为0.258，“好”的隶属度为0.336，“较好”的隶属度为0.231，“一般”的隶属度为0.091，“差”的隶属度为而0.084，由最大隶属度原则，可评判该高职物理教学多元智能水平为“好”这一等级。

2、从表1的计算结果可以看出：在影响高职物理教学多元智能水平的一级因子中，知识与技能、过程与方法的影响最大，分别占到38%和34%；在二级因子对一级因子的影响中，数学-逻辑智能、自然智能、人际交往智能相应于各自一级因子的影响较大，分别占到4%、52%一级43%；在二级因子对高职物理教学多元智能水平的总体影响中，数学-逻辑智能、自然智能、语言智能、人际交往智能以及身体-运动智能影响力较大，分别到占24.3%、17.7%、12.2%，12.0%和11.2%，因此，在提高高职物理教学多元智能水平过程中，应当着重加强这几个方面能力的培养。

［1］闫莉.基于多元智能理论的学生评价研究［D］.西安：西安电子科技大学，2010.

［2］陈银杏，曾青云.多元智能理论与高职教育教学改革［J］.中国成人教育，2015，（13）：144-149.

［3］姜启源.数学模型［M］.北京：高等教育出版社，1987.

［4］虞晓芬，傅玳.多指标综合评价方法综述［J］.统计与决策，2004，（11）：119-121.

G712

A

1671-5993（2016）02-0052-03

2016-02-15

安徽省质量工程教学研究项目（2012jyxm687）；滁州职业技术学院院级质量工程基金项目（zlgc2012037）。

梁金荣（1980-），女，安徽灵璧人，讲师，硕士，主要从事物理学教育教学研究。