基于R-W方法的多自由度的运动特性研究及应用

梁 夏，吴晓光，张 弛

（武汉纺织大学 机械与自动化学院，湖北 武汉 430200）

基于R-W方法的多自由度的运动特性研究及应用

梁 夏，吴晓光*，张 弛

（武汉纺织大学 机械与自动化学院，湖北 武汉 430200）

基于罗伯森和威藤堡提出的R-W方法，针对一种新型全自动鞋套机的驱动系统，开展了多刚体动力学R-W方法的探讨。提出研究鞋套机的驱动系统的基本建模思路，建立了鞋套机的驱动系统的多刚体动力学模型及运动方程，论证R-W方法对特殊机械可行性；通过ADAMS软件对已建立的鞋套机驱动系统进行动力学仿真，其数学模型与虚拟仿真结果基本一致；通过部分数值分析和仿真分析，为设计新型无纺布专用鞋套机结构设计、关键驱动零部件优化设计提供可靠的分析依据。

无纺布鞋套机；R-W方法；多刚体运动；仿真

为解决塑料鞋套易产生静电以及对环境的污染等问题，利用无纺布易分解，可循环再利用等特点，设计了一款全自动无纺布鞋套机。然而鞋套机驱动系统影响到整个系统的工序转换的稳定性和生产的效率，对其分析研究十分重要。鞋套机驱动系统为复杂的空间结构，运用经典力学方法研究其运动规律已经很难解决驱动系统中多个零部件相互作用。罗伯森和威藤堡提出的R-W方法为其提供了强大的理论武器，它是以多个相互作用的刚体组成的复杂系统为研究对象，结合计算机技术，对其进行运动学和动力学分析。本文将采用多刚体系统动力学中提出的R-W方法来建立鞋套机驱动系统的数学模型，并结合ADAMS综合对其进行动力学仿真分析，以获得最佳的数据。

1　鞋套机驱动系统多刚体模型建立

1.1 全自动无纺布鞋套机系统的描述

全自动无纺布鞋套机的模型主要有进料装置、对折装置、中心驱动装置、夹具、出料装置、机架和包缝机等组成。原料上采用了无纺布解决了塑料鞋套弹性问题和白色污染；技术上采用全自动缝合技术提高了生产率，减轻了劳动强度。中心驱动装置是全自动鞋套机驱动系统研究的重点，是整个鞋套机的重要组成部分，在工作过程中，电机带动中心旋盘绕椭圆形轨道做圆周运动，完成无纺布原料到鞋套成品的工序。鞋套机驱动系统结构图如图1所示。

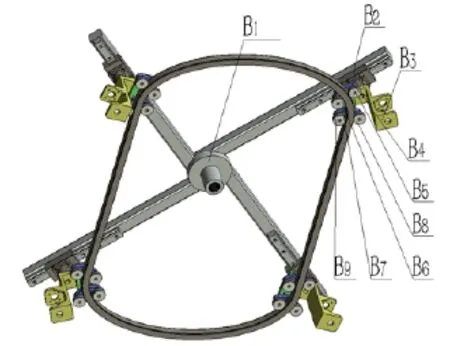
图1　鞋套机驱动系统结构图

1.2 模型的建立及运动方程

全自动无纺布鞋套机驱动系统为9个刚体相互约束连接的模型。根据图1鞋套机驱动系统结构图内分体的联接和相对运动，确定鞋套机驱动系统的拓扑构型。按照多刚体动力学中R-W的理论，B0表示鞋套机机架，B1表示旋转十字架，B2表示直线滑块，B3表示支撑架，B4、B7表示鞋套机机身导轮支撑，B5、B6、B8、B9表示导轮。将连接相连刚体的有向线段记做铰hj(j=1,2…,9)，其中h2为移动副，其他铰为转动副。选用R-W图论方法，得到如图2所示的鞋套机驱动系统有向图。为了能获得其树形系统的运动学方程，简化鞋套机驱动系统的非树形结构为树形结构。分割掉鞋套机驱动系统有向图中铰h11、h12、h13和h14，获得如图3所示的鞋套机树形系统图。

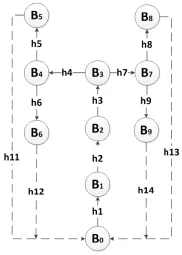
图2　鞋套机驱动系统有向图

图3　鞋套机树形系统图

依据R-W理论确定各刚体连体基，设机架的连体基为（O0,e0）。设各刚体的内接铰为hj(j=1,2…,9)且其中h2（滑移铰）、hj(j=4,5,6,7,8,9)均与质心重合，且均为单自由度转动铰，则派生树共有9个自由度。

则可得鞋套机驱动系统的关联矩阵S和通路矩阵T为：

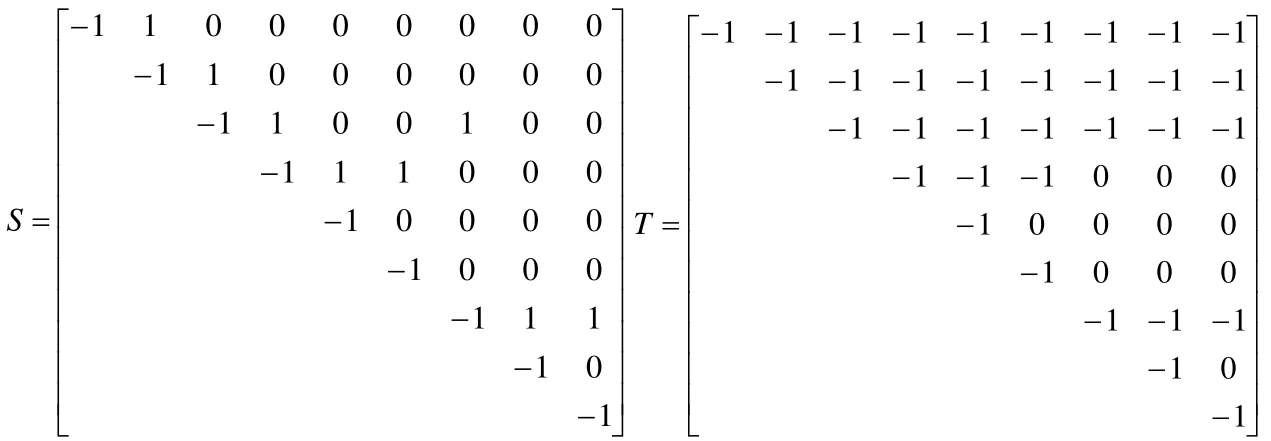
设机架B0和中心旋转盘B1的连体基（Oi,ei）(i=0,1)重合，为垂直轴,并且相等。B2的质心O2在轴上，z2为h2铰的滑移距离，规定内接铰hi指向质心Oic的距离为iρ，内接铰hi指向外接铰hi+的距离为Lij(j=1,2,3为连体基轴的方向)。

则通路矢量为：

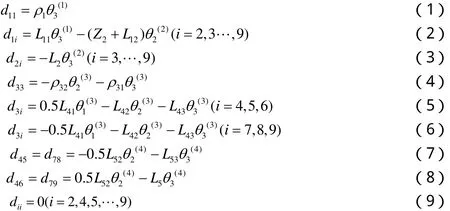
即可得通路矢量dij构成的矩阵为：

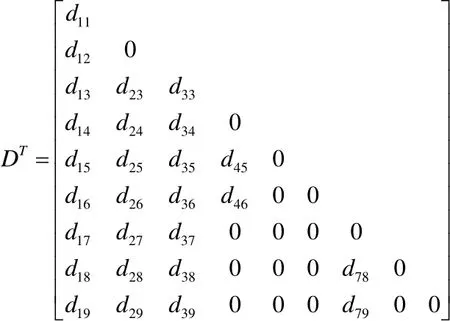
综上可得鞋套机树形系统中各刚体质心构成的运动方程[2]为：式中[r]——由Bi刚体质心位置ir矢径构成的矩阵；

r0——刚体B0质心矢径；

[1]n——元素为1的nx1维列阵；

[D]——为通路向量dij构成的nxn矩阵。

1.3 约束方程

鞋套机驱动系统以中心旋盘为主刚体，其余为附件的旋转运动。ρ是以轨道中心为原点，α为椭圆长半轴，b为椭圆短半轴的极坐标参数方程，滚轮沿着这个轨道做圆周运动[3]。轨道简图如图4所示。

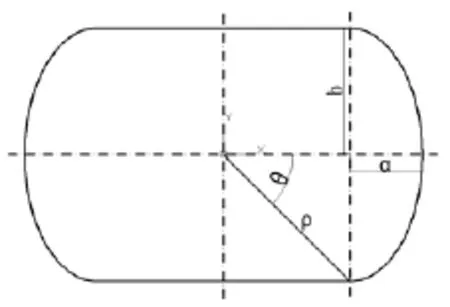
图4　轨道简图

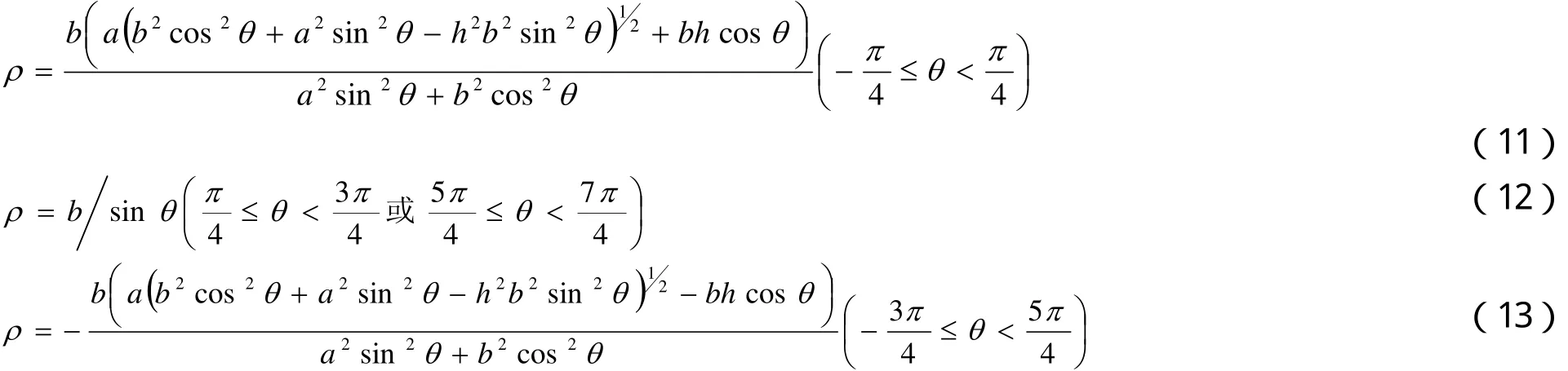
2　模型仿真分析

2.1 MATLAB的仿真分析

根据以上内容列出的鞋套机驱动系统各刚体数学模型，在MATLAB中编写程序进行仿真研究[4-5]，其中鞋套机驱动系统数学模型的相关参数，如质心到铰点的向量，各刚体的尺寸等运用SolidWorks估算和测量，中心旋盘以30°/s旋转得到滑块的响应曲线如图5所示。

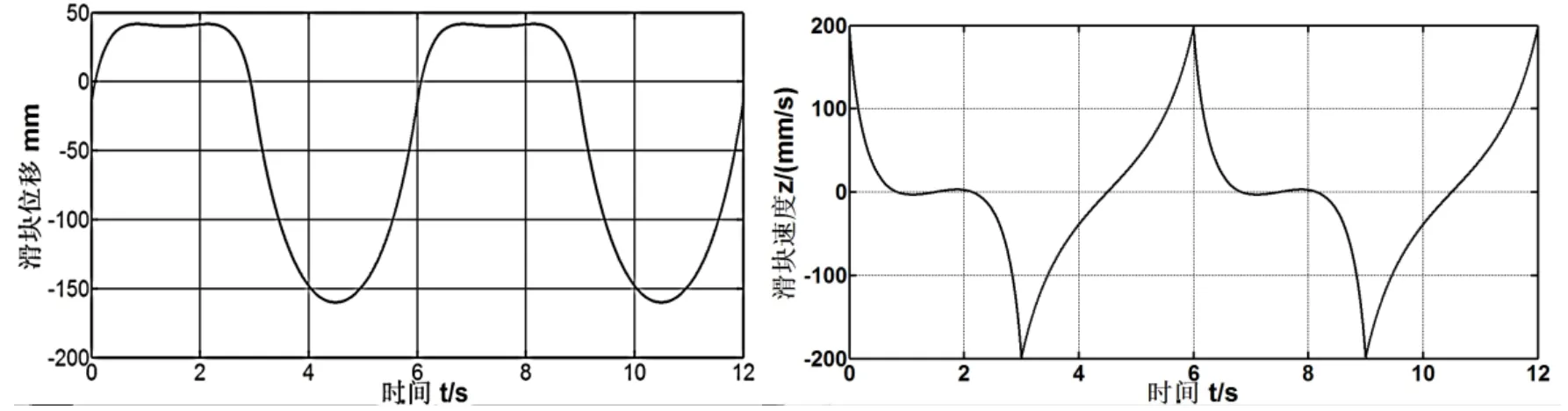
图5　MATLAB中计算的位移、速度曲线

2.2 基于ADAMS的仿真分析

在Adams中，鞋套机驱动系统虚拟样机如图6所示。为了获得鞋套机驱动系统虚拟仿真研究与实际工作状态一致的结果，需要对导入的每个零部件的相关属性进行编辑，如材料、质量、转动惯量等。再设置各个零件的运动关系，完成各运动部件之间的连接副和驱动，对专用鞋套机进行运动学及动力学仿真。其中运算和求解的各参量矩阵是根据力学模型获得的，然后建立了系统相关数学模型。最后选取专门的多刚体系统动力学数值分析算法迭代求解，并分析其结果[6]。

图6　专用鞋套机驱动系统虚拟样机

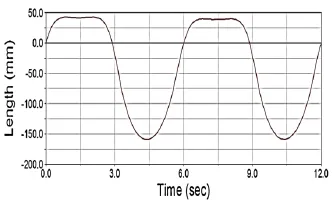
图7　滑块位移响应曲线

图8　滑块速度响应曲线图

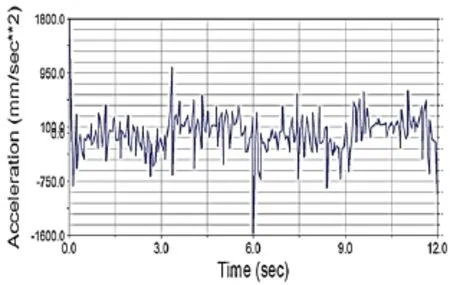
图9　加速度响应曲线

从图5、图7和图8可以看出，基于MATLAB和ADMAS对鞋套机的仿真结果基本吻合，证实了所建立模型的有效性。滑块的位移大约-175～50mm变化，是从轨道直线与半椭圆相切处开始运动，满足半椭圆-直线-半椭圆-直线的运动规律。从图8可以看出滑块的速度曲线趋势基本与图5一致，但出现微小的波动，这是由于沿着轨道运动的两滚轮中心距比轨道宽0.5mm，受力状态不均匀引起的。图9为滑块的加速度响应曲线，可以看出，启动瞬间加速度比较大，在一定范围波动。

3　结论

本文应用多刚体动力学中的R-W理论，以铰的相对坐标为独立变量，对鞋套机驱动系统进行抽象与简化，建立与实际机械系统一致的数学模型，对鞋套机驱动系统进行空间运动学数值分析，研究鞋套机驱动系统的运动规律。再结合数字化虚拟样机开发工具ADAMS对专用鞋套机进行动力学分析，得到各个零件的位移、速度、加速度等运动规律，有效的研究了系统动态特性。同时，通过对比证实了R-W方法研究特殊机械的可行性。全自动无纺布鞋套机的研究目前在国内尚首空白，文中的理论研究与产品研究将为此款机型实用化奠定基础，为正在研究类似工作的工程技术人员提供参考。

[1] 刘延柱，潘振宽，戈新生，多体系统动力学[M]. 北京：高等教育出版社，2014.

[2] 宁介雄，钟志强，张建军，等．多刚体学R-W方法对双摇臂机构的优化[J]．建筑机械化，2010，4（11）：42-45.

[3] 王鹏程，方勇纯，相吉磊，等．回转旋臂式船用起重机的动力学分析和建模[J]．机械工程学报，2011，47（20）：34-40.

[4] 齐朝晖．多体系统动力学[M]．北京：科学出版社，2008.

[5] 韩清凯，罗忠．机械系统多体动力学分析、控制与仿真[M]．北京：科学出版社，2010.

[6] 陈力平，张云清，任卫群，等．机械系统动力学分析及ADAMS应用教程[M]．北京：清华大学出版社，2005.

Research and Application of Multi-degree of Freedom Motion Characteristics Based on R-W Method

LIANG Xia, WU Xiao-guang, ZHANG Chi
(School of Mechanical Engineering and Automation, Wuhan Textile University, Wuhan Hubei 430200, China)

This paper has proposed a basic modeling in studying the driving system of this shoe-cover machine, built the multi rigid-body dynamical model and motion equations of this system, and proved the effectiveness and feasibility of R-W method to the special machine. Through ADAMS software, the dynamic simulation of this established driving system has been analyzed, and the outcomes are basically consistent with that of its mathematical model. Through numerically analyzing and simulation analysis, this paper can provide reliably analytic references for the design of structure of a new type special non-woven fabric shoe cover machine and the optimized design of key driving components and parts.

shoe cover machine; R-W method; multi rigid body motion; simulation

TU311.3

A

2095－414X(2016)03－0048－04

吴晓光（1954-），男，教授，研究方向：数字化纺织装配及关键技术.