非线性振动系统非共振振动自同步特性*

2016-08-03耿志远魏小鹏闻邦椿

振动、测试与诊断 2016年2期

关键词：非线性

李　叶，　耿志远，　李　鹤，　魏小鹏，　闻邦椿

(1.东北大学机械工程与自动化学院　沈阳，110819) (2.中国科学院沈阳自动化研究所　沈阳，110016)

非线性振动系统非共振振动自同步特性*

李叶1，耿志远2，李鹤1，魏小鹏1，闻邦椿1

(1.东北大学机械工程与自动化学院沈阳，110819) (2.中国科学院沈阳自动化研究所沈阳，110016)

摘要从理论计算、数值仿真和实验验证三个方面研究一类平面单质体非线性振动系统在非共振工作时的振动同步特性。首先，以反向回转双电机驱动的振动系统为研究对象，考虑其弹性元件的非线性因素，采用拉格朗日法建立其动力学模型；其次，基于Hamilton原理求出系统实现自同步的条件，利用一次近似判别法求出系统稳定同步运行的条件；然后，基于Matlab/Simulink软件，采用4阶龙格库塔法进行数值仿真，对理论推导的自同步条件及稳定性条件进行计算；最后，对一单质体振动样机进行实验测试。仿真结果表明，该非线性振动系统可以实现稳定的0相位自同步运动。通过理论计算结果、仿真结果以及实验结果的相互对比，验证该非线性振动系统同步特性理论的准确性。

关键词非线性；非共振；振动系统；振动同步；同步稳定性

引言

近年来，许多国内学者对自同步振动机械系统的机电耦合特性进行了大量的研究，得到了许多关键性的成果。文献[1-3]建立了电机系统和振动机械系统的机电耦合数学模型，从机电耦合的角度定量再现了系统的机电耦合同步机理。侯勇俊等[4]采用Matlab/Simulink对三电机驱动自同步振动系统的机电耦合机理进行了数值仿真。由于振动系统中多电机驱动源的振动同步常常与系统的非线性特性联系在一起，很多学者开始从非线性特性分析角度研究系统的同步性能。刘极峰等[5]通过振动同步性试验研究了非线性空间双质体振动烘干机在振动阻尼条件下实现振动同步应满足的条件。郭虎伦[6]研究了非线性因素条件下相位差角与振幅的关系，讨论了相位差角的变化对于同步效率的影响，进一步分析了系统中的非线性现象。陈会征[7]依据振动筛分设备的发展特点，在振动筛及自同步系统的研究基础上，将非线性共振筛结构与自同步原理结合，研究了超大型高效节能筛多点激励的稳定性。李小号[8]应用平均法对含有分段线性弹性元件的非线性振动系统的锐共振振动同步与控制同步进行了研究。Balthazar等[9]通过数值仿真的方法研究了安装在非线性架上的多个非理想激振器的自同步问题。

基于前人的研究，笔者以一类非线性振动系统为对象，基于拉格朗日方程建立该系统的动力学方程；运用Hamilton原理推导出该系统实现自同步的条件；采用非线性系统稳定性一次近似判别法求出振动系统在平衡点处的渐进稳定条件。以某单质体振动同步样机为例，基于其实际结构参数进行数值仿真。最后，对该振动样机进行自同步实验。将理论计算、仿真与实验结果进行对比，验证自同步理论的合理性。

1非线性振动系统自同步理论计算

1.1非线性振动系统动力学方程

图1为由两反向旋转的电机驱动的非线性振动系统的平面力学模型，由振动质体及两偏心转子组成。振动质体在水平和竖直方向分别通过弹簧A和B与固定支架相联。考虑弹簧的硬特性非线性，即刚度随变形增加而增大，其特性曲线如图2所示，其弹性力表达式为

F=kx+k′x3

(1)

其中：F为弹性力；k，k′均为弹簧刚度系数，可由实验曲线求出；x为弹簧压缩量。

图1　非线性振动系统的力学模型Fig.1　The mechanical model of nonlinear vibration system

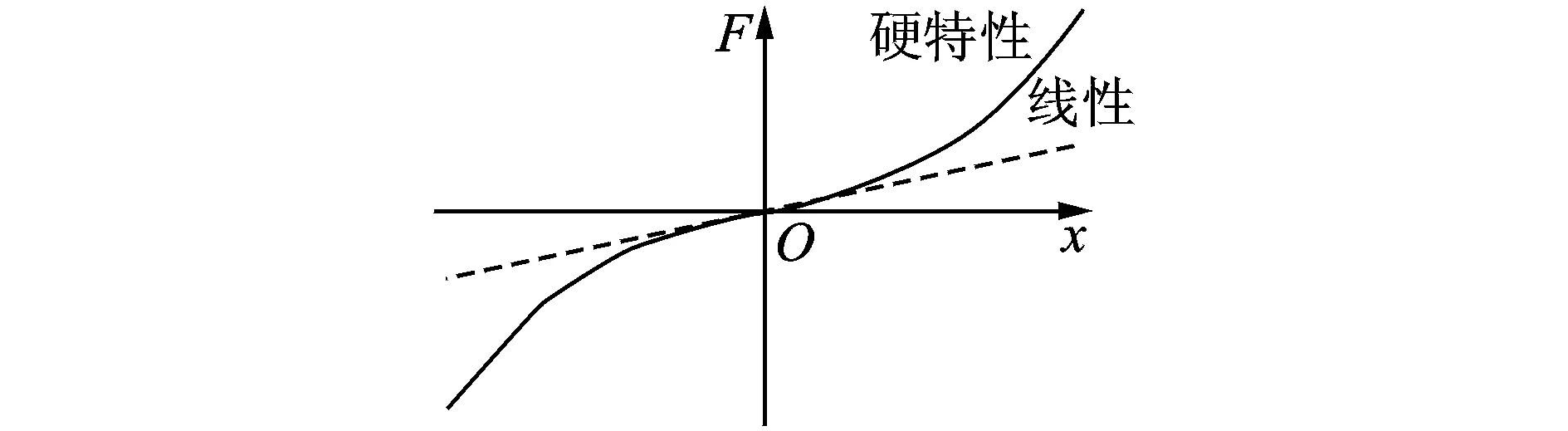
图2　弹簧弹性特性曲线Fig.2　The stiffness property curve of spring

两偏心转子安装在振动质体上方左右两侧，分别由感应电机1,2驱动。旋转中心o1和o2关于质体质心所在竖直轴对称。电机旋转时，偏心块产生激振力，带动质体发生水平、竖直方向的振动以及摆动。

选择质体运动坐标x，y，ψ及两转子的旋转相位φ1和φ2为广义坐标，求出系统的动能、势能和耗散能函数，代入拉格朗日方程得系统的运动方程式

(2)

根据驱动电机的机械特性[10]，电磁转矩Te与转速n的关系，即电机的输出电磁转矩数学模型为

(3)

1.2两偏心转子的自同步条件

设振动系统稳态运行时两偏心转子的平均相位为φ，且φ=ωt，ω为两电机的平均角速度；设偏心转子1超前于偏心转子2的相位为2α，则偏心转子1和2的相位分别表示为

(4)

(5)

对于式(5)，由渐进法可求得振动系统非共振状态下各向的一次近似稳态解为

(6)

其中：各向振动幅值及滞后角为

(7)

其中：kex，key和keψ为各向等效刚度系数，即

拉格朗日函数为

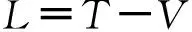
(9)

在一个振动周期内，哈密顿作用量可表示为

(10)

(11)

其中

(12)

根据Hamilton原理，即系统哈密顿作用量的变分与作用在系统上的非有势力所作用的虚功在一个周期内的积分和为零，表示为

(13)

其中：qi为广义坐标；Fi为广义力。

(14)

将式(11),(12),(14)代入到式(13)中，可求得

sin2α=TD/TC

(15)

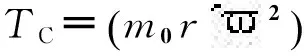
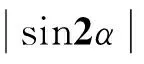
(16)

可得双机驱动反向旋转平面单质体非线性振动系统自同步实现的条件，即两电机的频率俘获力矩的绝对值大于或等于两电机剩余电磁转矩差的绝对值。

当|TD/TC|≤1，2α满足以下两个区间：a. 当0≤TD/TC≤1时，相位差2α在[0,π]区间; b. 当-1≤TD/TC<0时，相位差2α在[-π,0)区间。

1.3两偏心转子的自同步稳定性条件

设fd1=fd2，则式(2)后两式，即两偏心块的运动方程可化为

(17)

(18)

其中

(19)

根据式(18)求出系统对应的平衡点方程[8]为

(20)

由式(20)得，当

(21)

时，可求系统平衡点(arcsinΔTe/T′, 0)。由该平衡点及式(18)可知，当系统在该点稳定时，系统可出现零角速度差的同步运转。对式(18)平衡点处进行相平面奇点分析，取式(18)的特征方程为

(22)

解得其特征根为

li=

其中：i=1,2。

由非线性系统稳定性的一次近似判别法，当所有特征根均具有负实部时系统稳定，则只需

T′cose1>0

(23)

时，系统在相平面上具有渐进稳定焦点，即(arcsinΔTe/T′,0)，则式(23)为系统振动同步运行在平衡点处的渐进稳定条件。

2数值仿真

基于振动系统的动力学方程式(2)以及电机的电磁转矩模型式(3)，采用Matlab/Simulink对系统进行数值仿真，采用的计算方法为4阶龙格库塔法，步长为0.01 s，仿真时长为60 s。振动系统及电机的主要参数如表1所示。图3为振动系统各参数仿真结果。

由图3看出，在整个启动过程中两电机一直处于同步状态。两激振电机最终以990.6 r/min的转速稳定运行，实现了速度同步；整个过程中两电机的相位差恒为0，实现了相位同步。振动系统仅有竖直方向位移的变化，在系统启动5 s后表现为振幅约为2.605 mm的周期运动，其水平方向和扭摆均产生微小振动，与竖直方向位移相比可忽略为0。

表1电机及振动系统参数

Tab.1The parameters of motors and vibration system

参数/单位数值异步电机飞轮转动惯量J0/(kg·m2)0.062电机过载倍数KT2电机额定功率PN/kW0.040电机额定转速nN/(r·min-1)900电机电网转速ns/(r·min-1)1000电机轴摩擦阻力矩系数fdi/(N·(rad·s-1)-1)0.010振动系统总质量M/kg38.640偏心转子质量m/kg3.880振动系统转动惯量J/(kg·m2)1.288偏心转子等效偏心距r/m0.013水平方向刚度系数kx/(N·m-1)24000竖直方向刚度系数ky/(N·m-1)40000水平方向非线性刚度系数k'x/(N·m-3)4844311竖直方向非线性刚度系数k'y/(N·m-3)8073852水平和竖直方向阻尼系数fx,fy/(N·(m·s-1)-1)200弹簧A可动点与y轴的距离lyA/m0.225弹簧A可动点与质体质心水平线的距离lxA/m0.005转子中心至质体质心距离l0/m0.172转子与质心连线与x向夹角β/(°)30

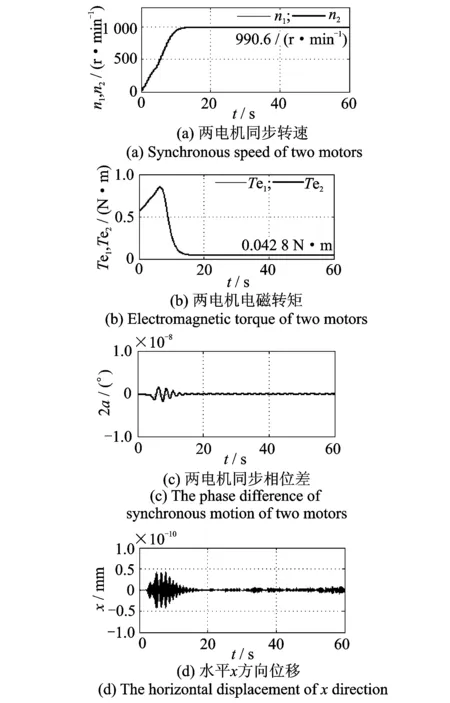
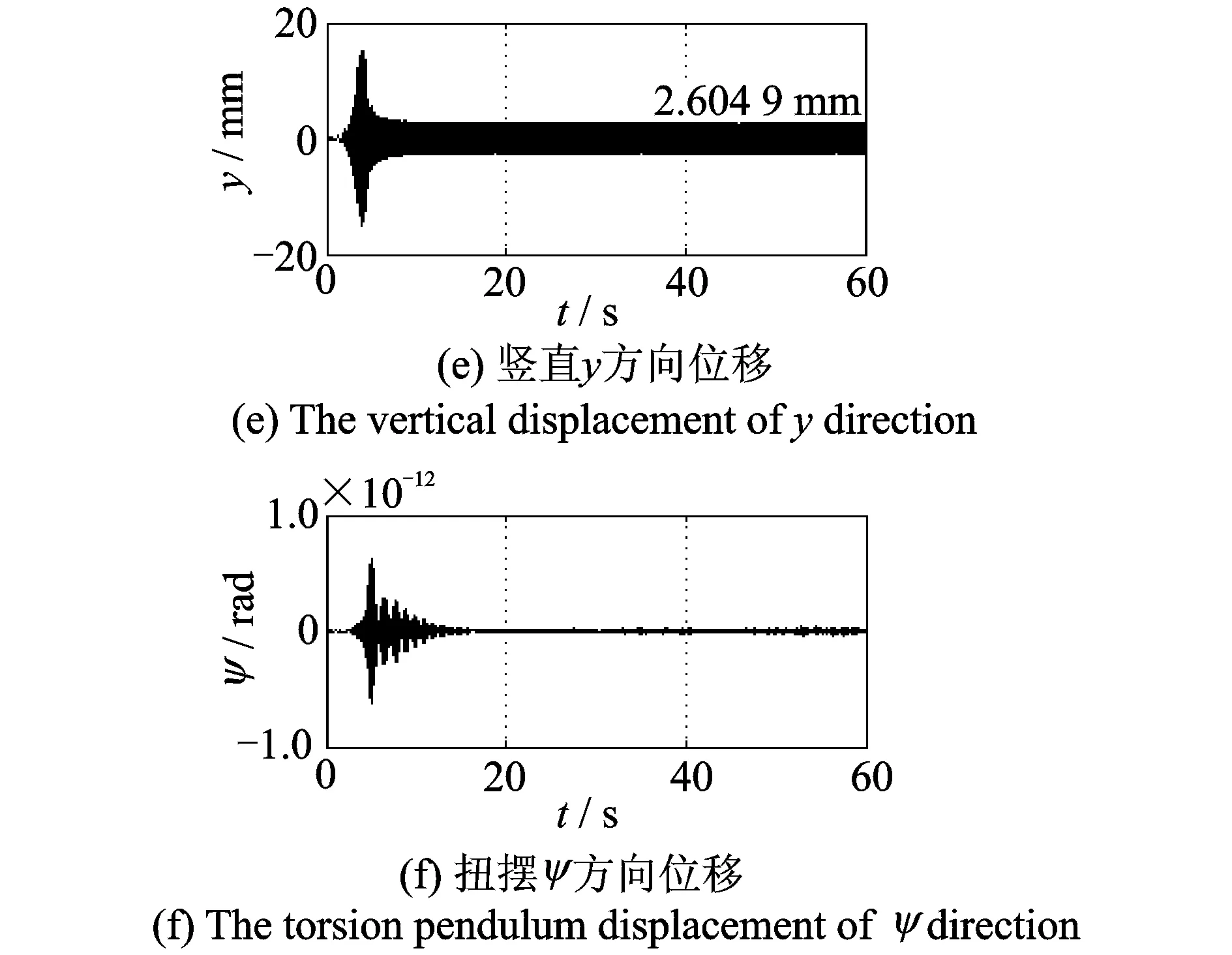
图3　系统的各参数仿真结果Fig.3　The simulation results of each parameter of system

将计算的电机转速代入到式(7)、(12)、(15)和(19)中，计算结果如图4所示。可以看出，由于两电机参数相同，整个过程中电机的剩余电磁转矩差TD始终为0，频率俘获力矩TC约为-0.68 N·m；相位差角2α为0；水平振动、竖直振动以及摆动的振幅ax，ay，aψ分别为0，2.826，0 mm。系统的稳定性系数T′为0.679 N·m，则T′cos2α>0，满足稳定性条件。图4(g)为系统的相轨迹，可以看出系统在零相位差、零角度差处具有稳定焦点。综上可知，计算结果与仿真结果基本一致，证明了自同步理论推导的准确性。

3实验验证

振动自同步实验样机如图5所示。样机包括两台MVE100/1型号三相异步振动电机(即激振器)、振动质体以及ROSTA-AB15型号弹性振动支撑，其弹性特性为非线性硬特性。实验中信号的采集和分析均用B&K振动测试分析系统，如图6所示。当两电机实现自同步后，所得振动系统各参数结果如图7所示。

由图7看出，同步时两电机转速达到990 r/min，达到了速度同步；偏心块的相位差角度稳定在约为0.023°，达到了相位同步；振动系统x方向、y方向以及ψ方向的振动在系统启动一段时间后都表现为周期运动。其中，x方向和ψ方向的振动幅度分别约为0.1 mm和0.004 rad，在实际工程中数值很小，均可忽略不计；y方向的振幅约为3 mm。

图4　系统各参数理论计算结果Fig.4　The theoretic calculated results of each parameter

图5　自同步振动实验样机Fig.5　Self-synchronization vibration test prot-otype

图6　B&K振动测试分析系统Fig.6　B&K vibration tes-ting and analyzing system

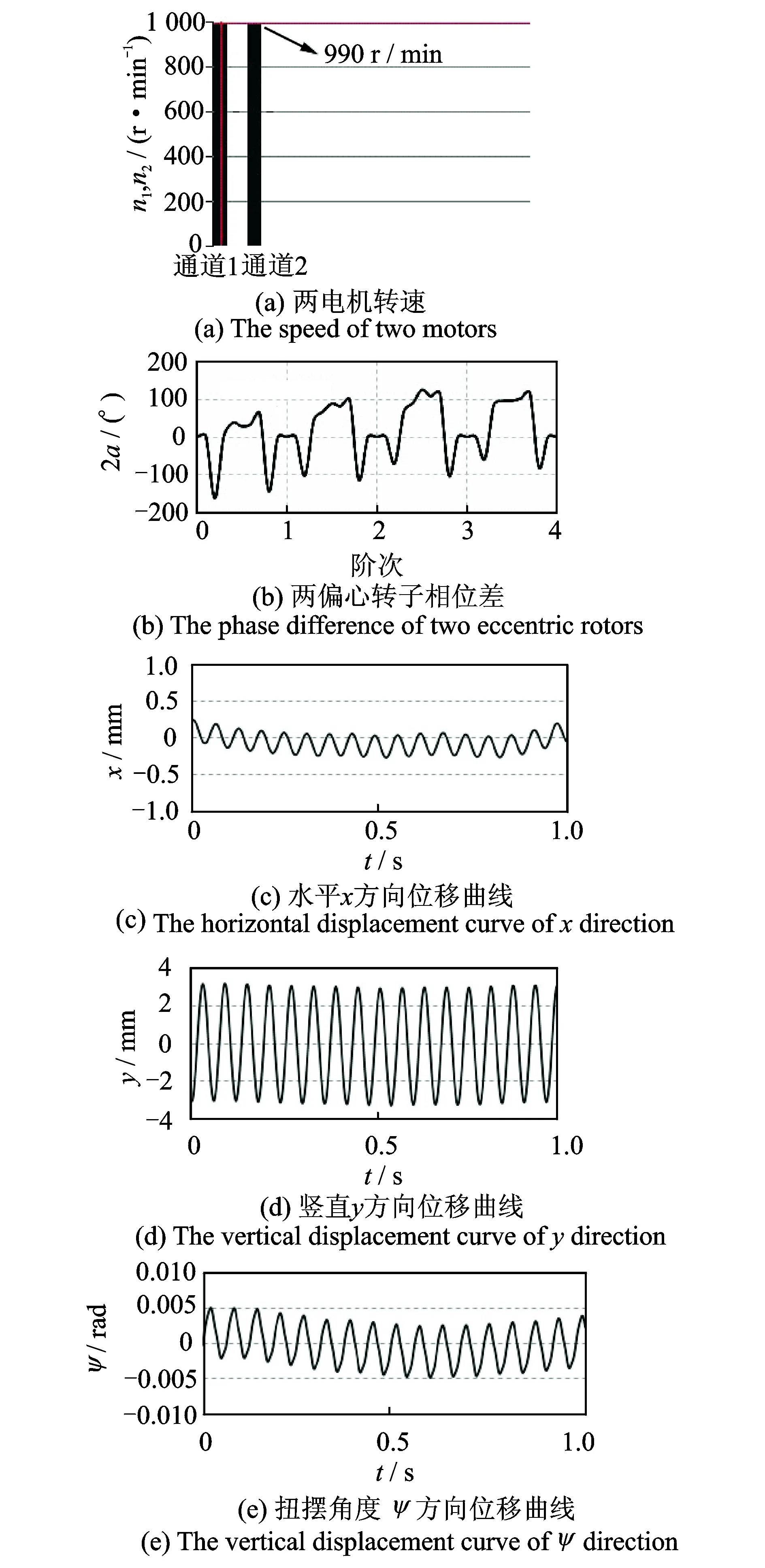
图7　系统各参数实验结果Fig.7　Experimental results of each parameter of system

综上可见，实验样机在实现自同步时各实验结果与理论计算、数值仿真结果存在很小误差，这主要是由于振动机自身及外界因素对实验结果具有一定影响，在工程中可以忽略不计。因此，在一定程度上验证了仿真结果的准确性和有效性。

4结论

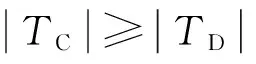
2) 当T′cose1>0时，系统在相平面上具有渐进稳定焦点，且该点即为非线性振动系统平衡点(arcsinΔTe/T′,0)。

3) 采用Matlab/Simulink软件，运用4阶龙格库塔法对振动系统进行了数值仿真。由仿真结果可以看出，振动系统在达到稳定状态时可以实现0相位的自同步运动。当系统完全对称，两偏心转子反向回转时，振动系统只产生竖直方向的振动。将仿真结果与理论计算结果对比可以看出，各参数值基本一致，验证了理论推导的准确性。

4) 对一单质体非线性振动样机进行了自同步实验。由实验结果与仿真结果对比可以看出，系统实现自同步时各参数数值误差较小，实验结果合理，在一定程度上验证了理论计算与数值仿真的准确性和有效性。

参考文献

[1]Zhang Tianxia, Wen Bangchun, Fan Jian. Study on synchronization of two eccentric rotors driven by hydraulic motors in one vibrating system[J]. Shock and Vibration, 1997, 4(5-6):305-310.

[2]王得刚,姚红良,冯霏,等.自同步振动系统的动力学耦合特性及实验[J].振动、测试与诊断, 2012, 32(S): 53-58.

Wang Degang, Yao Hongliang, Feng Fei, et al. Dynamic coupling feature and experimental study of self-synchronous vibrating system[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(S): 53-58. (in Chinese)

[3]Zhang Xueliang, Zhao Chunyu, Wen Bangchun. Theoretical and experimental study on synchronization of the two homodromy exciters in a non-resonant vibrating system[J]. Shock and Vibration, 2013, 20(2): 327-340.

[4]侯勇俊,闫国兴.三电机激振自同步振动系统的机电耦合机理[J].振动工程学报,2006,19(3):354-358.

Hou Yongjun, Yan Guoxing. Electromechanical-coupling mechanism of self-synchronous vibrating system with three-motor-driving[J]. Journal of Vibration Engineering, 2006, 19(3): 354-358. (in Chinese)

[5]刘极峰,陈旋,马履中.非线性振动烘干机的振动阻尼与振动同步研究[J].农业机械学报,2007,38(2):87-89.

Liu Jifeng, Chen Xuan, Ma Lüzhong. Vibration amortization and vibration synchronism of nonlinear vibrator dryer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(2): 87-89. (in Chinese)

[6]郭虎伦.非线性自同步振动机动力学行为分析[D].哈尔滨:哈尔滨工业大学,2008.

[7]陈会征.超大型高效节能筛多点激励稳定性分析[D].哈尔滨：哈尔滨工业大学，2011.

[8]李小号.非线性振动系统锐共振振动同步与控制同步关键技术研究[D].沈阳:东北大学,2010.

[9]Balthazar J M, Felix J L, Brasil R. Some comments on the numerical simulation of self-synchronization of four non-ideal exciters [J]. Applied Mathematics and Computation, 2005, 164(2): 615-625.

[10]谢丽蓉,王智勇,晁勤.鼠笼异步电动机机械特性的研究[J]. 中国电机工程学报,2008,28(21):68-72.Xie Lirong, Wang Zhiyong, Chao Qin. Research on the mechanical characteristic of squierrelcage asynchronous motors[J]. Proceedings of The CSEE, 2008, 28(21):68-72. (in Chinese)