有限策略集全序解及其生成算法

陈少白，熊丽琼，张　嫚

(1.武汉科技大学理学院，湖北 武汉，430065；2. 武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉,430065)



有限策略集全序解及其生成算法

陈少白1,2，熊丽琼1，张嫚1

(1.武汉科技大学理学院，湖北 武汉，430065；2. 武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉,430065)

根据策略之间的两两比较结果，将策略集中的所有策略排出顺序是人们在决策时的一个基本依据。本文提出最小全序解的概念，并分别给出偏序策略集、预序策略集以及任意关系策略集最小全序解的表示及其生成算法。

策略集；最小全序解；偏序关系；全序关系；决策

决策理论在社会科学、管理科学以及人工智能等研究领域已经得到广泛应用[1-2]。人们在进行决策时，往往先对策略集X中的策略进行两两优劣比较，其结果用二元关系R来表示，从而形成策略集关系。根据比较的结果将所有的策略依优劣程度排出一个合理的次序，这是人们在决策时的一个基本依据，而效用理论、偏好理论以及信念的度量等均与排序相关[3]。举一个简单的例子：球队进行比赛，怎样合理地用比赛结果形成的胜负关系将球队排出名次。人们习惯用数值来量化这种优劣关系，于是有两个基本问题：①找到一个函数f，使得当(x,y)∈R时，有f(x)≥f(y)成立；②这种函数在何种意义下唯一，如何将它确定出来。由于在做决策时不在乎策略对应的数值大小，只需对各种策略排出优劣次序，即对于单射f:X→(-∞,+∞)，确定一个二元关系T：T={(x,y)∈X×X|f(x)≥f(y)}，T具有自反性、传递性和完全性。于是问题转变成：①找到X上的全序关系T，使得当(x,y)∈R时，总有(x,y)∈T成立；②在何种意义下这种全序关系是唯一的，求出全体这样的全序关系。针对上述问题，本文提出最小全序解概念，并分别给出偏序策略集、预序策略集以及任意关系策略集最小全序解的表示及其生成算法。

1　最小全序解

以下X表示n个元素的有限集合，T是X上全序关系的全体，A′=X-A是A的补集，Rc是二元关系R的逆关系，I={(x,x)∶x∈X}是恒等关系。

定义1设R是X上二元关系，如果有T∈T，使得R⊂T，称R可以全序表示，T是R的一个全序表示。

X上二元关系R与S的距离用对称差ρ(R,S)=|R-S|+|S-R|来度量，其中|·|表示集合中元素的个数。

对于任意关系，不一定有全序表示，以距离二元关系R最近的全序关系作为二元关系R的最佳排序。

定义2对于集合X上二元关系R，距离R最近的全序关系全体记为T(R)，即

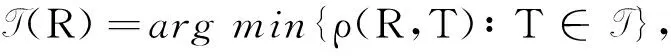
称T(R)中元素为二元关系R的最小全序解，简称全序解，其中，argmin表示使得ρ(R,T)达到最小的全序关系T的集合。

二元关系的全序解有如下四种等价形式。

定理1对于X上二元关系R，以下四项是等价的：

(1)T(R)=argmin{|R-T|+|T-R|∶T∈T}；

(2)T(R)=argmin{|R-T|∶T∈T}；

(3)T(R)=argmin{|T-R|∶T∈T}；

(4)T(R)=argmax{|R∩T|∶T∈T}。

证明：对于任意T∈T，总有

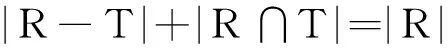
以及

定理2如果二元关系R可以全序表示，则T(R)={T∈T∶R⊂T}。

证明：如果关系R可全序表示，则存在T0∈T，使得R⊂T0。对于T∈T(R)，由于|R∩T|≥|R∩T0|=|R|，得R⊂T，即

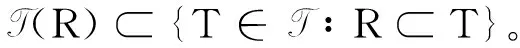
对于T∈T，R⊂T，由|R∩T|=|R|≥max{|R∩T|∶T∈T}，得T∈T(R)，即

证毕。

以下分别确定偏序关系、预序关系以及任意二元关系R的全序解T(R)，并给出其全序解的生成算法。

2　偏序关系的全序解

满足自反性、传递性的关系为预序关系，满足反对称性的预序关系为偏序关系，如果R∪Rc∪I=X×X，称R是完全的。如果S是X上偏序关系，R⊂S，称S是关系R的保序扩展；如果S还是X上全序关系，称S是R的全序扩展。

定理3设R是X上预序关系，(x0,y0)∉Rc，记R+=R∪R(x0,y0)，其中R(x0,y0)={(x,y)∶(x,x0),(y0,y)∈R}，则

(1)R(x0,y0)≠∅，

(2)R∩Rc(x0,y0)=Rc(x0,y0)∩R(x0,y0)=∅，

(3)R(x0,y0)∘R(x0,y0)=∅，

(4)R∘R(x0,y0)=R(x0,y0)∘R=R(x0,y0)。

其中：Rc(x0,y0)表示R(x0,y0)的逆关系；“∘”表示二元关系的复合关系。

证明：(1)R是X上自反的关系，有(x0,y0)∈R(x0,y0)，所以R(x0,y0)≠∅。

(2)如果(x,y)∈R∩Rc(x0,y0)，即(x,y)∈R，(y,x0),(y0,x)∈R，由R的传递性得(y0,x0)∈R，与条件(x0,y0)∉Rc不合，所以R∩Rc(x0,y0)=∅；

如果(x,y)∈Rc(x0,y0)∩R(x0,y0)，即(y,x0),(y0,x)∈R，(x,x0),(y0,y)∈R，由R的传递性得(y0,x0)∈R，与条件(x0,y0)∉Rc不合，所以Rc(x0,y0)∩R(x0,y0)=∅。

(3)如果(x,y)∈R(x0,y0)∘R(x0,y0)，即存在z∈X，使得(x,x0),(y0,z)∈R、(z,x0),(y0,y)∈R，根据R的传递性得(y0,x0)∈R，与条件(x0,y0)∉Rc不合，所以R(x0,y0)∘R(x0,y0)=∅。

(4)根据R的传递性，显然有R∘R(x0,y0)=R(x0,y0)∘R=R(x0,y0)。证毕。

定理4设R是X上预(偏)序关系，如果(x0,y0)∉Rc，则R+是X上预(偏)序关系。

证明：设R是X上预(偏)序关系，因R⊂R+，所以R+是自反的。根据定理3，

=R∩Rc

所以R+与R具有相同的反对称性。由于

所以R+具有传递性，即：R+是X上预(偏)序关系。证毕。

如果(x0,y0)∉Rc，当(x0,y0)∈R时，R+=R，R+没有增加任何有序对，当(x0,y0)∉R时，相对R而言，R+至少增加一个有序对(x0,y0)。如果R是X上偏序关系，则R+是R的保序扩展。

定理5集合X上偏序关系R经过有限次保序扩展后必为全序关系；每一个包含偏序关系R的全序关系，总可以由该类保序扩展得到。

证明：R是X上偏序关系，如果R∪Rc=X×X，即R是完全的，则R是X上全序关系；如果R∪Rc≠X×X，则将R保序扩展成R+，直至R∪Rc=X×X，所以偏序关系R经过有限次保序扩展最终成为全序关系。对于任意R⊂T的全序关系T，如果(R∪Rc)′≠∅，选(x0,y0)∈T∩(R∪Rc)′，则R+⊂T，T包含由偏序关系R经过有限次扩展而成的全序关系，所以T是R的一个保序扩展。证毕。

推论1R是X上偏序关系，则

T(R)={T∈T∶R⊂T}，

其中T(R)为二元关系R的全序解集合。

推论2对于X上任意二元关系R，总有:T(R+)⊂T(R)。

以下给出偏序关系R的全序解T(R)的生成算法：

步骤1如果R∪Rc=X×X，结束；否则转步骤2。

步骤2取(x,y)∈X×X-R∪Rc，得到R的两个扩展R1=R∪R(x,y)与R2=R∪R(y,x)，分别转步骤1。

例1对于集合X={1,2,3,4}，其偏序关系R={(1,1),(1,2),(1,3),(1,4),(2,2),(2,4),(4,4),(3,3)}，求它的全部全序解。

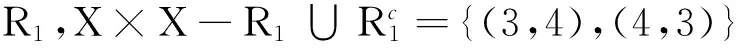
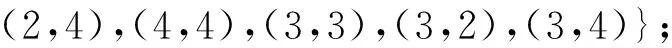
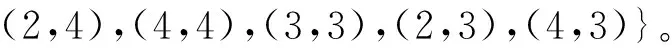
即对应的3个排序分别为：1,3,2,4；1,2,3,4；1,2,4,3。

3　预序关系的全序解

设R是X上预序关系，I={(x,x)∶x∈X}是恒等关系，将预序关系R分解成：R=(R-Rc)∪(R∩Rc)，则有以下结论。

定理6如果R是X上预序关系，则(R-Rc)∪I是X上偏序关系。

证明：(R-Rc)∪I显然满足自反性与反对称性。对于(x,y),(y,z)∈R-Rc，由R的传递性有(x,z)∈R，如果(z,x)∈R，则由(y,z)∈R-Rc，得(y,x)∈R，与(x,y)∈R-Rc矛盾，所以(x,z)∈R-Rc。证毕。

显然，R∩Rc是X上等价关系。

定理7设R是X上预序关系，则T(R)={T∈T∶R-Rc⊂T}。

证明：由于

|R∩T|=|(R-Rc)∩T|+|(R∩Rc)∩T|

所以|R∩T|达最大，当且仅当|(R-Rc)∩T|达最大，即T(R)=T(R-Rc)，又(R-Rc)∪I是一个偏序关系，所以T(R)={T∈T∶R-Rc⊂T}。证毕。

由于T(R)=T(R-Rc)，可依照偏序关系的全序解生成算法计算T(R-Rc)。

4　一般二元关系的全序解

对于序列x1,x2,…,xr，r>1，如果x1≠xr，称{(x1,x2),(x2,x3),…,(xr,x1)}为圈；如果x1,x2,…,xr两两不同，则称为简单圈，{(x,x)}称为自圈。显然，圈至少包含一个简单圈。

定理8关系R的传递闭包t(R)有圈当且仅当R有圈。

于是有正整数m1,m1,…,mr，分别使得(xi,xi+1)∈Rmi，i=1,2,…,r，所以R有圈。证毕。

推论3设R是X上二元关系，自反、传递闭包rt(R)是偏序关系的充分必要条件是R无圈。

定理9若R是X上无圈二元关系，则T(R)=T(rt(R))={T∈T∶rt(R)⊂T}。

证明：如果R是X上无圈二元关系，对于全序关系T，R⊂T当且仅当rt(R)⊂T。又自反、传递闭包rt(R)是偏序关系，所以T(R)={T∈T∶rt(R)⊂T}。证毕。

定理10二元关系R有唯一全序扩展的充分必要条件是：R为无圈、完全的关系。当条件成立时，R的唯一全序扩展为rt(R)。

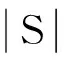
对于任意T∈T，S=R-T总是R的一个破圈，事实上，S⊂R，而R-S=R∩T是无圈的。

定理11设R是X上二元关系，如果S为R的一个最小破圈，则R-S的全序扩展T∈T(R)；如果T∈T(R)，则R-T为R的一个最小破圈，即T(R)={T∈T∶R-S⊂T,S∈S},其中，S为R的一个最小破圈全体。

证明：设R是X上二元关系，S0为R的一个最小破圈，T0为R-S0的全序扩展。对于任意T∈T，令S=R-T，则S⊂R且R-S=R∩T无圈，S为R的一个破圈，于是|S0|≤|S|。由于|R|=|R-S|+|S|=|R-S0|+|S0|，得|R-S|≤|R-S0|。又因为R-S0⊂T0，有R-S0⊂R∩T0，得|R∩T|≤|R∩T0|，所以T0∈T(R)。

设T0∈T(R)，令S0=R-T0，则S0⊂R，且R-S0=R∩T0，即S0为R的一个破圈。对于R的任意一个破圈S，由于R-S无圈，有全序扩展T∈T，使得R-S⊂T，得R-T⊂S，注意到R=(R-T)∪(R∩T)=(R-T0)∪(R∩T0)以及|R∩T|≤|R∩T0|，得|S0|=|R-T0|≤|R-T|≤|S|，所以S0=R-T0为R的一个最小破圈。证毕。

以下给出任意关系全序解T(R)的生成算法：

步骤1计算出所有简单圈O1,O2,…,Om；

步骤2从每个简单圈中选一条边，组成边集合Lk，k=1,2,…,|O1×O2×…×Om|，求出|Lk|达最小的边集合Lk，得到最小破圈边集合；

步骤3求R-Lk的自反、传递闭包rt(R-Lk)，它是一个偏序集；

步骤4将rt(R-Lk)全序扩展，得到全序关系。

例2设X={1,2,3,4}，关系R={(1,3),(3,1),(3,2),(1,4),(2,4),(4,2)}，求其全序解。

解：计算出所有的简单圈：

确定最小破圈边集合：

可得：

然后通过步骤3和步骤4的运算，最终得到全序解T(R)：3,1,4,2；3,1,2,4；1,3,4,2；1,3,2,4。

5　结语

人们在决策前会进行策略之间的比较，这种比较出来的策略集关系是一个二元关系。在对策略进行排序时，合理的选择是：将关系集中最接近的全序关系作为策略集的排序，这种全序关系不唯一，形成了一个最小全序解集合。本文给出最小全序解的表示及其生成算法，可用于指导决策。

[1]KatsikopoulosKV,GigerenzerG．One-reasondecision-making：modelingviolationsofexpectedutilitytheory[J].JournalofRiskandUncertainty，2008，37(1)：35-56．

[2]AndreoniJ,SprengerC.Certainanduncertainutility：theAllaisParadoxandfivedecisiontheoryphenomena[Z].Levine’sWorkingPaperArchive，2010：1-20．

[3]WongSKM,YaoYY,BollmannP,etal.Axiomatizationofqualitativebeliefstructures[J].IEEETransactionsonSystems,ManandCybernetics, 1991, 21(4):726-734.

[责任编辑尚晶]

Totalordersolutionofafinitestrategysetanditsgeneratingalgorithm

Chen Shaobai1,2，Xiong Liqiong1，Zhang Man1

(1.CollegeofScience,WuhanUniversityofScienceandTechnology,Wuhan430065,China;2.HubeiProvinceKeyLaboratoryofSystemsScienceinMetallurgicalProcess,WuhanUniversityofScienceandTechnology,Wuhan430065,China)

Allstrategiesinthestrategysetaresortedaccordingtothecomparisonresultsbetweenstrategies,whichisafundamentalbasisforpeopletomakedecision.Thispaperproposestheconceptofminimaltotalordersolution,andprovidestherepresentationsandgeneratingalgorithmsoftheminimaltotalordersolutionsofstrategysetswithpartialorder,pre-orderandarbitraryrelation,respectively.

strategyset;minimaltotalordersolution;partialorderrelation;totalorderrelation;decisionmaking

2016-01-25

湖北省自然科学基金资助项目(2013CFA131).

陈少白(1957-)，男，武汉科技大学教授，博士.E-mail:chenshaobai71@163.com

O225

A

1674-3644(2016)04-0317-04