步进式加热炉内板坯温度场模拟分析

金　明，倪红卫，张　华，孔勇江，郭满平

(1.武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉，430081；2.武汉钢铁股份有限公司炼钢总厂，湖北 武汉，430083)



步进式加热炉内板坯温度场模拟分析

金明1，倪红卫1，张华1，孔勇江2，郭满平2

(1.武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉，430081；2.武汉钢铁股份有限公司炼钢总厂，湖北 武汉，430083)

以某公司热轧带钢厂的三段步进式加热炉为研究对象， 通过建立三维数学模型，运用ANSYS软件分析板坯在炉内加热过程中的温度分布，并研究炉内均热段的温度和保温时间及氧化铁皮厚度对板坯温度场的影响。结果表明，板坯加热后最高温度分布在板坯端面角部，最低温度位于板坯中心部位 ，在设定的加热制度下,板坯经炉内加热后，其出炉温度、断面温差分别为1273.48、12.91 ℃，板坯温度分布比较均匀，满足轧制要求；随着均热温度的下降，板坯的出炉温度随之降低，而断面温差变化较小；随着保温时间的缩短，板坯的出炉温度变化不大，而断面温差明显增大；随着板坯表面氧化铁皮厚度的增加，板坯中心部位的温度明显降低、断面温差明显增大；在设定的加热制度下，适当降低均热段的温度和缩短保温时间，并控制板坯表面氧化铁皮的厚度，有利于提高板坯加热质量和节能降耗。

加热炉；板坯；温度场；均热温度；保温时间；氧化铁皮；温度模拟

板坯加热在钢铁材料生产过程中占有很重要的地位。不少研究者对板坯加热过程进行了模拟研究，文献[1-2]针对推钢式加热炉建立了一维数学模型，用有限差分法离散了板坯的导热微分方程，得到了板坯的温度场；青格勒等[3]建立三段步进式加热炉内板坯加热过程的二维数学模型，分析了板坯在加热炉内的温度变化情况；冯亮花等[4]建立了加热炉内板坯加热过程的二维数学模型，采用有限容积法对模型进行离散，模拟了板坯的温度场；有研究者开发了一套加热炉内火焰图像在线检测系统，为步进式加热炉内三维温度场的检测提供了可视化手段[5-7]。目前对板坯加热过程的一维和二维温度场模拟研究较多，对三维温度场的模拟研究有待深入，同时应考虑板坯表面氧化铁皮对其温度分布的影响。为此，本文以某公司热轧带钢厂的三段步进式加热炉为研究对象， 通过建立三维数学模型，运用ANSYS软件分析板坯在加热过程中的温度分布，并研究炉内均热段的温度和保温时间及氧化铁皮厚度对板坯温度场的影响，为优化步进式加热炉内板坯的加热工艺提供参考。

1　数学模型

1.1模型假设

某公司热轧带钢厂步进式加热炉的炉体有效长度为43.6 m，板坯在炉内加热过程中依次经过预热段、加热段和均热段，其中加热段又分加热一段和加热二段[8]。由于板坯在炉内加热是一个复杂的物理化学变化过程，建立模型时做如下简化和假设[9]：①忽略板坯加热过程的内热源；②同一时刻板坯各节点的热物性参数相同；③不考虑板坯传热的端部效应；④所研究截面传热是对称的；⑤板坯与辊道的接触传热忽略不计；⑥炉墙热特性和炉气黑度不随时间和温度变化；⑦不考虑步进梁与板坯之间的传热，认为板坯周围全是炉气；⑧板坯与炉气的对流、辐射传热视为与无限大环境的传热。

1.2导热微分方程

基于上述假设，在直角坐标系下建立板坯的导热微分方程：

(1)

式中：λ为板坯的导热系数，W/(m·K)；CP为板坯的比热，J/(kg·K)；T为板坯的温度，K；ρ为板坯的密度，kg/m3；x，y和z分别为板坯长度、宽度和厚度方向的坐标，m。

1.3加热板坯的热物性参数

加热板坯的钢种为DX51D+Z，其化学成分见表1、导热系数和比热见表2。板坯规格为0.23 m×1.30 m×8.80 m，板坯的密度为7850 kg/m3。板坯表面氧化铁皮的导热系数为3.2 W/(m·K)、比热为725 J/(kg·K)、密度为3950 kg/m3[10]。

表1　DX51D+Z钢的化学成分(wB/%)

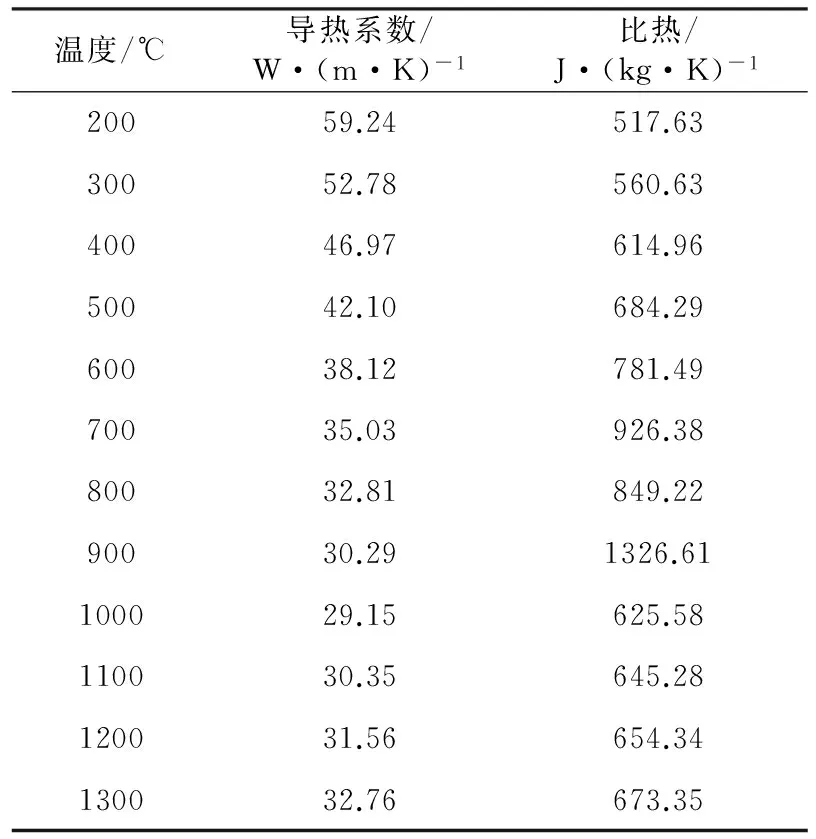
表2　不同温度下DX51D+Z钢的导热系数及比热

1.4初始条件和边界条件

初始条件为：板坯入炉温度为190 ℃。

边界条件包括对流、辐射边界和绝热边界。板坯外表面与炉气接触，是对流、辐射边界，板坯对称面是绝热边界。

当炉气流过钢坯表面时，钢坯表面不仅通过对流方式从炉气中得到热量，而且依靠炉气的辐射得到热量，总热流量的计算公式为[8]：

(2)

变形后得：

q=∂c(tg-tm)+∂r(tg-tm)

=∂Σ(tg-tm)

(3)

其中：

(4)

上述式中：q为总热流量；tg、tm分别为炉气和钢坯表面温度，℃；C为气体对固体表面辐射的导来辐射系数,W/(m2·K4)；∂c为对流换热系数，W/(m2·K)；∂r为辐射换热系数，W/(m2·K)；∂Σ为综合换热系数(∂Σ=∂c+∂r)，W/(m2·K)；εg为实际炉气黑度，取0.213；εm为板坯黑度，取0.79；σ为斯蒂芬玻耳兹曼常数，σ=5.67×10-8W/(m2·K4) ；φm为炉壁对钢坯表面的角系数，其值为1。

1.5几何模型和网格划分

运用ANSYS软件，取板坯的1/8进行建模，选定建模尺寸(单位：m)，设定建模比例为1∶1。采用手动划分的方式对所建模型进行网格划分，长度方向进行50等分，宽度方向进行20等分，厚度方向进行10等分，网格划分如图1所示。

图1　板坯的网格图

2　模拟结果与分析

2.1板坯的温度分布

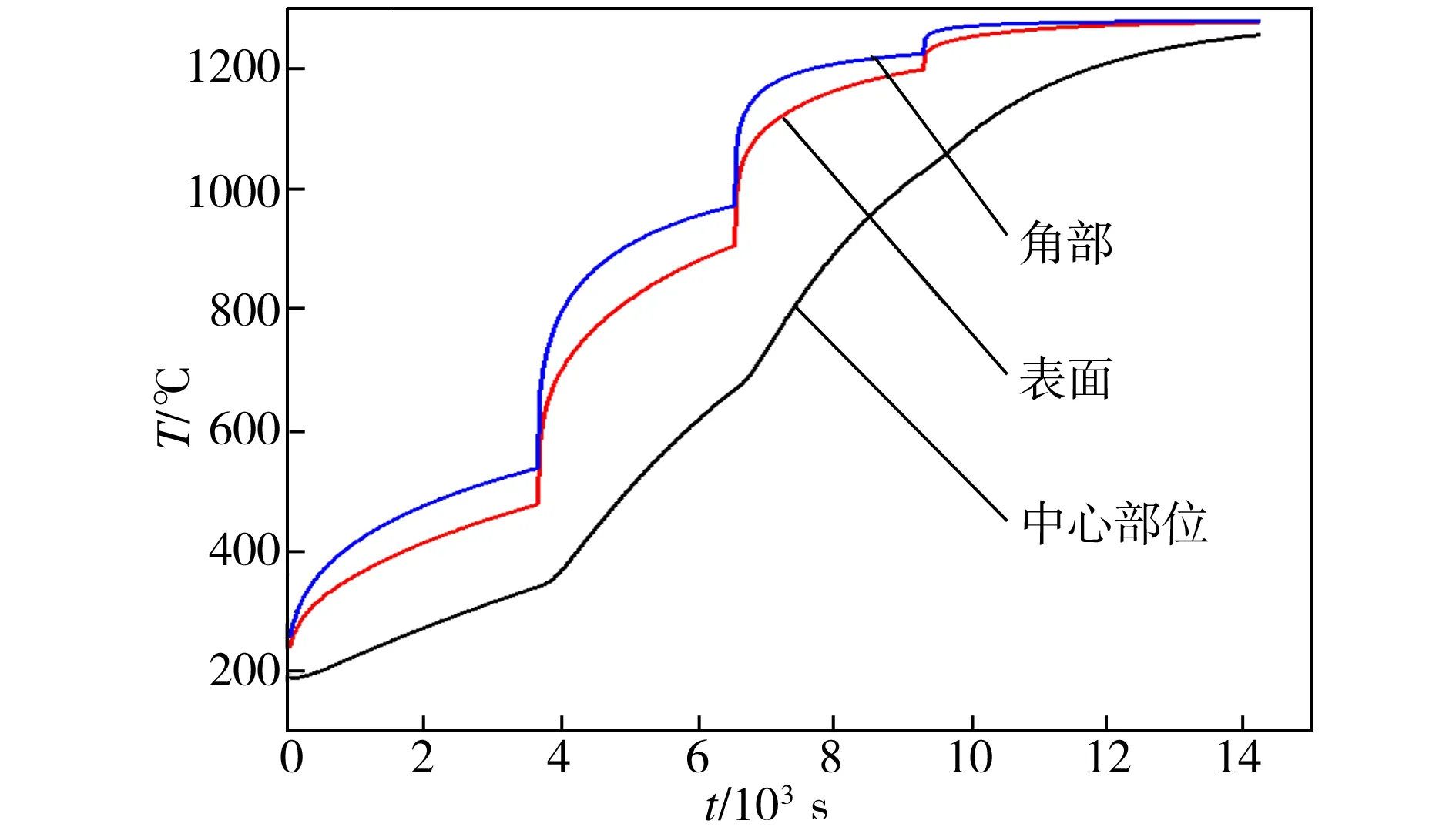
某公司热轧带钢厂板坯的加热制度如表3所示。板坯的出炉温度要求在1000～1300 ℃范围内，断面温差控制在25 ℃以内。在此加热制度下，板坯的角部、表面(取板坯长度1/2位置横断面)、中心部位的温度分布曲线如图2所示，板坯出炉后的温度分布如图3所示。从图2中可以看出，在加热过程中，板坯中心部位与板坯表面、角部的的温差先增大后减小，这是因为，在预热段和加热一段，板坯的初始温度与环境温差大，板坯表面的升温速率明显高于中心部位，进入加热二段和均热段，板坯表面温度不断上升，与环境温差逐渐缩小，加热热量主要用于板坯内部升温，此时板坯中心部位的升温速率迅速超过板坯表面的升温速率。经计算得到，在炉内预热段、加热一段、加热二段和均热段，板坯表面升温速率分别为4.59、8.99、6.49、0.96 ℃/min，而板坯中心部位的升温速率分别为2.59 、7.16 、8.05 、2.49 ℃/min，板坯表面和中心部位的最大温差分别为124.97、296.57、329.56、158.26 ℃。从图3中可以看出，板坯经炉内加热后，其出炉温度为1273.48 ℃，角部和中心部位的温差为14.25 ℃，断面温差为12.91 ℃，表明板坯的温度分布相对均匀，满足轧制的要求。从图3中还可看出，板坯的最高温度分布在板坯端面的角部，最低温度位于板坯的中心部位，这是因为，板坯角部与炉气直接接触，其加热条件最好，致使板坯角部温度最高，而板坯中心部位的热量需要先通过炉气的对流和辐射综合传热给板坯表面，再由板坯表面通过热传导传热到板坯中心部位，因此板坯中心部位的温度最低。

表3　板坯的加热制度

图2　加热过程中板坯不同部位的温度分布曲线

图3　板坯出炉后的温度分布

2.2板坯温度分布的影响因素

2.2.1均热温度

当保温时间为80 min时，不同均热温度下板坯的出炉温度和断面温差如表4所示。从表4中可以看出，随着均热温度的下降，板坯的出炉温度随之降低，断面温差逐渐缩小。与现有加热制度下设定的均热温度(1280 ℃)相比，均热温度降低30 ℃时，板坯的出炉温度降低28.87 ℃，断面温差减小1.91 ℃；均热温度降低60 ℃时，板坯出炉温度降低57.94 ℃，断面温差减小3.50 ℃；而当均热温度升高30 ℃时，板坯出炉温度升高29.6 ℃，断面温差增大0.8 ℃。由此表明，均热温度对板坯出炉温度影响较大，而对断面温差影响较小。因此，在满足板坯最低出炉温度的条件下，可以适当降低均热温度，达到节能降耗的目的。

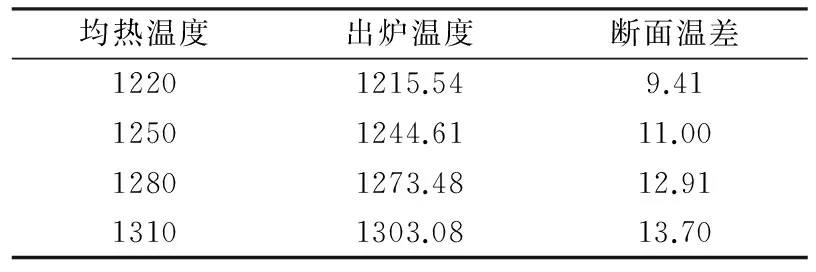
表4　不同均热温度下板坯的出炉温度和断面温差(单位：℃)

2.2.2保温时间

在1280 ℃的均热温度下保温不同时间后板坯的出炉温度和断面温差如表5所示。从表5中可以看出，随着保温时间的缩短，板坯出炉温度逐渐降低，断面温差明显增大。与现有加热制度下设定的保温时间(80 min) 相比，当保温时间缩短10 min时，板坯的出炉温度降低3.08 ℃，断面温差增大至18.08 ℃；保温时间缩短20 min时，出炉温度降低7.39 ℃，断面温差增大至25.27 ℃，已高出板坯所要求的出炉断面温差；而当均热时间延长10 min时，出炉温度升高2.18 ℃，断面温差减小至9.20 ℃。由此表明，均热段的保温时间对板坯断面温差影响较大，而对出炉温度影响较小。因此，在满足板坯断面温差要求时，可以适当缩短保温时间，达到节能降耗的目的。

表5　不同保温时间下板坯的出炉温度和断面温差

2.2.3氧化铁皮厚度

不同厚度氧化铁皮的板坯的温度分布曲线如图4所示。从图4中可以看出，虽然板坯表面氧化铁皮厚度不同，但板坯各部位的温度变化趋势基本一致，板坯表面温度变化不大，但中心部位的温度变化较为明显。与无氧化铁皮的板坯相比，当氧化铁皮厚2 mm时，板坯出炉时的表面温度降低了0.61 ℃，中心部位温度降低了8.86 ℃；而当氧化铁皮厚4 mm时，板坯出炉时的表面温度降低了1.35 ℃，中心部位温度降低了21.05 ℃。由此表明，随着板坯表面氧化铁皮厚度的增加，板坯中心部位的温度明显降低。

(a)0 mm

(b)2 mm

(c)4 mm

氧化铁皮的厚度对板坯出炉温度及断面温差的影响如表6所示。从表6中可以看出，随着板坯表面氧化铁皮的增厚，板坯出炉温度略有降低，但断面温差明显增大。与无氧化铁皮的板坯相比，当氧化铁皮厚2 mm时，板坯出炉温度降低了4.48 ℃，断面温差增大至21.16 ℃；而当氧化铁皮厚4 mm时，板坯出炉温度降低了10.63 ℃，断面温差已增大至32.61 ℃，大于板坯所要求的出炉断面温差。由此可见，板坯表面氧化铁皮的厚度对板坯加热质量影响较大，对于易生成氧化铁皮的钢种在确定其加热制度时，适当降低加热温度和缩短加热时间，以减少板坯的氧化烧损，从而控制板坯表面氧化铁皮的厚度。

表6　氧化铁皮厚度对板坯出炉温度及断面温差的影响

3　结论

(1)板坯在炉内加热后最高温度分布在板坯端面角部，最低温度位于板坯中心部位 ，在设定的加热制度下,板坯经炉内加热后，其出炉温度、断面温差分别为1273.48、12.91 ℃，板坯温度分布比较均匀，满足轧制要求。

(2)随着均热温度的下降，板坯的出炉温度随之降低，而断面温差变化较小；随着均热段保温时间的缩短，板坯的出炉温度变化不大，而断面温差明显增大；随着板坯表面氧化铁皮厚度的增加，板坯中心部位的温度明显降低、断面温差明显增大。

(3)在设定的加热制度下，适当降低均热段的温度和缩短保温时间，并控制板坯表面氧化铁皮的厚度，有利于提高板坯加热质量和节能降耗。

[1]陈海耿，杨泽宽，张卫军，等.太钢一轧厂加热炉数学模型优化控制[J].冶金能源,1995，14(4):39-43.

[2]李明.钢坯加热过程中氧化传热模型的研究[D].包头：内蒙古科技大学,2013.

[3]青格勒，程素森，杨天钧，等．步进梁式加热炉内的板坯温度场数值模拟[J]．北京科技大学学报，2004，26(2)：164-168．

[4]冯亮花，刘坤，康小兵，等．步进式加热炉板坯温度场数值模拟[J]．辽宁科技大学学报，2011，34(1)：39-43．

[5]娄春，周怀春，程强，等．工业炉内火焰图像在线检测系统及其试验[J]．工业加热，2005，34(3)：32-34．

[6]程强，周怀春，娄春，等．工业炉三维温度场可视化试验研究[J]．工业加热，2005，34(1)：19-23．

[7]邹敢，杨承志．加热炉钢坯温度场的预报模型[J]．青岛科技大学学报：自然科学版，2007，28(3)：250-252．

[8]蔡乔方.加热炉[M].北京:冶金工业出版社,2007.

[9]王良刚. 步进式加热炉内重轨钢坯温度场与应力场的数值模拟[D].包头： 内蒙古科技大学,2012.

[10]Martín Torres, Rafael Colás. A model for heat conduction through the oxide layer of steel during hot rolling[J]. Materials Processing Technology，2000, 105(3):258-263.

[责任编辑张惠芳]

Simulation analysis of temperature field of the slab in the walking beam reheating furnace

JinMing1,NiHongwei1,ZhangHua1,KongYongjiang2,GuoManping2

(1. Key Laboratory for Ferrous Metallurgy and Resources Utilization of Ministry of Education,Wuhan University of Science and Technology, Wuhan 430081, China;2.General Steelmaking Plant,Wuhan Iron and Steel Co., Ltd., Wuhan 430083, China)

With the 3-zone walking beam reheating furnace as the research object, the 3D mathematical model was established and the temperature field of the slab during the reheating process was analyzed by ANSYS . The effects of the temperature,the holding time of the soaking zone in the reheating furnace and the thickness of oxide scale on the temperature field of the slab were investigated. The results show that the highest temperature of the hot slab is located at the corner of the end face , and the lowest temperature is found at the central region of the hot slab. Under the given heating system, the tapping temperature and temperature difference in cross section of the slab after reheating are 1273.48 and 12.91 ℃, respectively. The temperature distribution of the slab is relatively uniform, which meets the requirements of rolling process. With the decrease of the soaking temperature,the tapping temperature of the slab decreases and temperature difference in cross section of the slab shows little change. With the decrease of the soaking time, the tapping temperature of the slab has little change while temperature difference in cross section of the slab is increased obviously. With the increase of the thickness of oxide scale, the central region temperature of the slab is dramatically decreased, and temperature difference in cross section of the slab increases significantly. Under the given heating system, by reducing the soaking temperature and soaking time and controlling the thickness of oxide scale properly at the same time, the reheating quality of the slab can be improved and energy consumption can be reduced.

reheating furnace; slab; temperature field; soaking temperature; soaking time；oxide scale; temperature simulation

2016-02-29

湖北省自然科学基金资助项目(2015CFA128).

金明(1990-)，男，武汉科技大学硕士生.E-mail:506112846@qq.com

倪红卫(1967-)，男，武汉科技大学教授，博士生导师.E-mail:nihongwei320@sohu.com

TG307

A

1674-3644(2016)04-0248-05