资本资产定价模型应用研究——对上海机电股份贝塔系数的测算

张 宸，高芸芸

（兰州理工大学 经济管理学院，甘肃 兰州 730050）

资本资产定价模型应用研究
——对上海机电股份贝塔系数的测算

张 宸，高芸芸

（兰州理工大学 经济管理学院，甘肃 兰州 730050）

经典的资本资产定价模型中所指的风险，按照是否可以利用多元化投资加以驱除区分为系统风险和非系统风险，而系统风险的大小主要靠β值进行测量。文章以上海机电股份为研究对象，运用图形分析和最小二乘法探究上海机电的预期收益率与风险之间的关系，并预测其β系数。实证结果说明：上海机电股份的风险与其收益之间显示出简单的线性关系，并且为正的线性相关关系；进一步通过预测其β系数发现该股票的风险比整体市场投资组合的风险要高，相应的其收益也大于整体市场投资组合的平均收益率。

贝塔系数；资本资产定价模型；上海机电股份

现代金融学理论的核心问题之一是权衡金融资产风险和收益之间的关系。经典的资本资产定价模型（CAPM）将资产的风险分为可以通过充分分散投资加以消除的特质风险和无法通过分散投资加以消除的系统风险（Markowitz，1952；Sharpe，1964）[1-2]。这一模型显示，一项资产的特定风险能够使用多元化分散投资完全消除掉，然而系统性风险无法完全清除，需要得到补偿。此时，该项资产的投资预期收益只由无风险利率、市场风险溢价以及用于描述该项资产市场风险程度的β系数决定，因此准确预测β系数，探究股票市场的预期收益率与其风险之间的关系就显得至关重要（郭艳萍，2013；王静，2015）[3-4]。

一、文献综述

（一）国内外关于资本资产定价模型的研究

1.资本资产定价模型的缘起与演进。Markowitz（1952）在“证券组合投资理论”中首次将资产定价理论定量化，对投资者行为进行了规范化，提出了一套完整的“均值-方差”分析框架，力求使投资多样化和预期收益这两个相互制约的指标达到均衡，标志着现代组合投资理论的开端（王静，2015）。之后，Sharpe等人（1964）在Markowitz（1952）研究的基础上，通过将单个投资者行为的研究转到研究整个市场，通过设定许多研究假设条件，创造性的构建出经典的资本资产定价模型。这些假设包括以下两点：第一，投资理性；第二，市场完全有效。

经典的资本资产定价模型形式如下：

E（rp）=rf+βp[E（rM）-rf]

模型中，E（rp）代表证券（P）或证券组合（P）的预期收益率；rf用来衡量资本市场中的无风险利率；βp表示证券或证券组合p的贝塔系数；E（rM）表示市场资产组合的期望收益率。

随着人们对该模型的逐渐熟悉，相关的思考更加深入，越来越多的困惑推动着模型向两个方向演进：第一，围绕经典资本资产定价模型，对其前提假设进行放宽和修改，相继提出了零β CAPM模型（Black，1972）[5]、跨期CAPM模型（Merton，1973）[6]以及消费CAPM模型（Breeden，1979），所有这些相关模型的推广使得经典的CAPM模型更加体系化，更加精细化，从而越加的接近于现实的市场环境；第二，另外一些学者继续延续资本资产定价模型按照能否通过多元化分散投资来将一项资产的风险区分为系统风险和特定风险的中心思想，但避开了先前的研究范式，探究出了新的研究思路和研究方法，从而进一步研究提出了新形式的资本资产定价模型。如期权定价模型（Slack& Scholes，1973）、多因素模型或套利定价理论（Ross，1976）[7]。所有这些演进共同丰富着资产定价理论（王晨曦，2015）[8]。

2.资本资产定价模型的检验。理论发展的演进与实证关系的检验总是密不可分的（王静，2015），之后学者们把该模型广泛应用在人力资本定价、战略管理、项目投资、社会保障（李媛媛，2013）[9]等领域，通过大量实证研究来检验风险—收益之间的关系，并得出以下三种结论：风险与收益正相关（Fama&Macbeth，1973[10]；Blume&Friend，1973；Tinic&West，1984；French等人，1987；Harrison&Zhang，1999；Bollerslev，1988；Bali&Peng，2006；Lanne&Luoto，2008；Jiang &Lee，2014；徐剑刚、唐国兴，1995；陈浪南、黄杰银，2002；陈守东等人，2003；刘勇、周宏，2005；陈梦根，2013[11]）、风险与收益负相关（Campbell，1987；Nelson，1991；Pagan&Hong，1991；Whitelaw，1994；Lettau&Ludivigson，2003；Brandt&Kang，2004；张思奇等人，2000；游宗君等人，2010[12]）以及风险与收益不相关（Chan等人，1992；何兴强、孙群燕，2003）或关系较为复杂（Turner等人，1989；Glosten等人，1993；Harvey，2001；Kinnunen，2014；刘金全、崔畅，2002；左浩苗、刘振涛，2011[13]；王天一等人，2014[14]）。可见，真实市场中的经验证据难以对传统资本资产定价模型中风险与收益正相关的理论提供有力支持（王静，2015）。然而一些学者认为以上检验所出现的矛盾性结论依赖于研究所选取的模型、外生变量（Harvey，2001）以及方差估计方法（Ghysels等人，2005；Bollerslev&Zhou，2006）等。

目前，国内外学术界和实务界对于资本资产定价模型的思考和探索仍未停止。认为其在未来至少有两大发展方向：第一，随着行为科学与经济学逐步深入地交叉，行为金融学研究兴起。这直接影响到资本资产定价模型的基础，即投资者理性假设和金融市场有效假设；第二，资本资产定价模型虽然最初用于金融资产收益率的测定，但是风险和不确定性无处不在，其内在的对风险的深刻洞见使其具有了向金融领域之外（人力资本定价、战略管理、项目投资等领域）推广应用的潜力（王晨曦，2015）。

（二）国内外关于β系数的研究

β系数作为资本资产定价模型最有意义的研究成果，其大小能够反映出某一风险资产所对应的风险与其收益之间的相关程度。夏普（1964）以及林特纳（1965）的相关研究成果表明某项风险资产按照其风险是否可以使用多元化分散投资加以消除来区分为系统风险和特质风险，其中特质风险能够利用多元化的投资组合有效进行清除，然而系统风险则是难以避免的，这部分难以避免的风险可以用风险系数（β系数）来表示。经典的CAPM模型假设系统风险β系数是个常量（夏普，1964），之后大量实证研究发现资本市场的系统风险显著不稳定（Andrew，1997[15]；靳云汇、刘霖，2001），β系数并非常量，而是实时变化的（Blume，1971[16]；Jagannathan&wang，1996[17]；陈浪南、屈文洲，2000；丁志国、苏治、赵晶，2012）[18]，并且不同状态下系统风险是不同的（刘丹红、张世英、苏为东，2003；简志宏、李彩云，2013[19]）。

可见，由于β系数是对未来系统风险的估计，而风险又是不确定的，因而不能很准确的确定出来β系数，它只是一个估计的值（阎志儒，2015）[20]。

综上研究发现，伴随着理论界对资本资产定价模型相关基础理论的丰富和发展，实务界也不断地将该理论广泛的应用于很多相关实践领域。本文借鉴前人的研究成果及相关理论，以上海机电股份为研究对象，运用计量经济学的最小二乘回归法估计上海机电股份的β系数，以验证前人的理论成果，从而丰富资本资产定价模型的应用。

二、理论基础

β系数体现了特定资产的价格对整体经济波动的敏感性，即股票与大盘之间的连动性，系统风险比例越高，连动性越强（张矢的、高明宇、吴斌，2014）[21]。其绝对值越大，显示其收益变化幅度相对于大盘的变化幅度越大；绝对值越小，显示其变化幅度相对于大盘越小（郭艳萍、李娇，2013）。

β值可能大于、等于或小于1（也可能是负值）。当β=1时，表示该资产的风险收益率与市场组合平均风险收益率呈同方向同比例变化，其风险情况与市场投资组合的风险情况一致；当β>1时，说明该单项资产的风险收益率高于市场组合平均风险收益率，则该单项资产的风险大于整个市场投资组合的风险；当β<1时，说明该单项资产的风险收益率小于市场组合平均风险收益率，则该单项资产的风险程度小于整个市场投资组合的风险（郭艳萍、李娇，2013）。

投资组合的β系数是所有单项资产β系数的加权平均数，权数为各种资产在投资组合中所占的比重。具体表示为βp=∑in=1Xiβi。 如果一个高β值股（β>1）被加入到一个平均风险组合（βp）中，则组合风险将会提高；反之，被加入到一个平均风险组合中，则组合风险将会降低。所以一种股票的β值可以度量该股票整个组合风险的贡献，β值可以作为对这一股票风险程度的一个大致度量（郭艳萍、李娇，2013）。

三、研究方法

已有研究发现，检验风险与收益之间的相关性的方法有滚动窗口模型（RW）、GARCH族模型、混合数据抽样方法（MIDAS）以及随机波动率一均值模型（SV-M模型）等等（王静，2015）。一些学者认为相较于RW模型和GARCH模型来讲，MIDAS方法模型可以更加准确的评估出一项资产的条件方差（Ghysels等人，2005）。最小二乘法是估计β系数最常用的方法，利用 Eviews6.0软件，对经典的资本资产定价模型中的参数值进行估计。本文以上海机电股份为研究对象，运用计量经济学的最小二乘回归法计算出上海机电股份的贝塔系数。

四、上海机电股份β系数的实证检验

（一）公司简介

上海机电股份有限公司（以下简称：本公司，原名上海上菱电器股份有限公司，经本公司2003年第二次临时股东大会决议更名为上海电气股份有限公司；经本公司2004年第一次临时股东大会决议更名为上海机电股份有限公司）是1993年7月29日经上海市经济委员会以沪经企字第331号文批准设立的股份有限公司。公司于1999年10月27日换领了注册号为企股沪字第019028号《企业法人营业执照》。本公司所发行普通股A股（600835）和境内上市外资股B股（900925），已在上海证券交易所上市。

公司主要经营机电一体化产品、设备的设计、生产，销售自产产品，提供相关售后服务；以上同类商品及技术的批发、进出口，提供相关配套服务。具体以相关政府部门的审批为准。公司是国内电梯产品的龙头企业，主营电梯及自动扶梯，约占国内市场份额的16%；主营的印刷机械业务主要来自全资子公司上海电气印机集团，主要产品在国内的市场占有率约37.6%；公司的冷冻空调业务主要来自于合资公司一冷开利，占市场份额15%以上。

（二）样本选取

本文选取2010—2014年共涉及 5年 的59个有效数据，来测算上海机电股份的β系数。为了保证数据的及时性以及准确性，该研究过程中所利用到的相关数据信息均来自深圳国泰安数据库。相关研究数据如表1所示，其中整体市场投资的回报率K（M）=（Pt-Pt-1）/Pt-1。其中，Pt代表的是第 t月月末的上证综指；Pt-1代表的是第t-1月月末的上证综指。

（三）模型构建

1.数据分析

利用 Eviews6.0软件进行计算检验，先对时间序列数据分析，首先将上海机电股份的股票收益率和大盘指数的收益率分别导入软件，绘制出上海机电股份的公司个股收益率和大盘整体收益率的散点图，如图1所示。

根据散点图可以大致看出所选样本的分布情况，由图1可知X和Y大致满足线性关系。即风险与收益之间存在着简单的线性相关性（陈小先，2014）[22]，并且为正相关关系，这与Sharpe等人（1964）的理论研究结论一致。按照以上图形显示出的线性规律性，从而能够构建出上海机电股份这一单个资产的β系数的相关一元线性回归模型Ki=βi×K（M）+ε。其中，Ki代表的是上海机电股份的月个股收益率；K（M）代表的是上海证券交易所的市场整体的收益率；ε代表的是模型的随机扰动项。

2.参数估计

从表2中可以看到，利用最小二乘估计法，计算出的上海机电股份的证券特征线的斜率，该直线的斜率代表的就是上海机电股份的β系数，采用 Eviews表，我们在相关自由度为59的条件之下，可以看出回归的临界值T（0.025 =2.000），同时解释变量 X的T值为3.052 872，且通过显著性检验，说明所选择的解释变量对被解释变量的影响是显著的。

3.回归结果分析

表1 相关数据

从以上回归结果（见表2）可以看出，调整后回归R2为12.54%，说明该模型的拟合优度良好。回归方程的斜率为0.672 539，说明上海机电股份2010年 2月至2014年 12月收益率的 β系数为 0.672 539>0，该结论说明上海机电股份这一风险资产的风险要比整个资本市场当中投资组合的风险要大，相应的其个股收益率也会大于整个资本市场当中投资组合的平均风险收益率。同时也说明，如果上证资本市场整体的综合指数每上升 1%，则相应的上海机电股份的个股收益率将会上升0.672 539%；反之亦然。可见上海机电股份受市场收益率变化的影响较大，投资者选择上海机电股份投资还是存在一定的风险。

图1 散点图

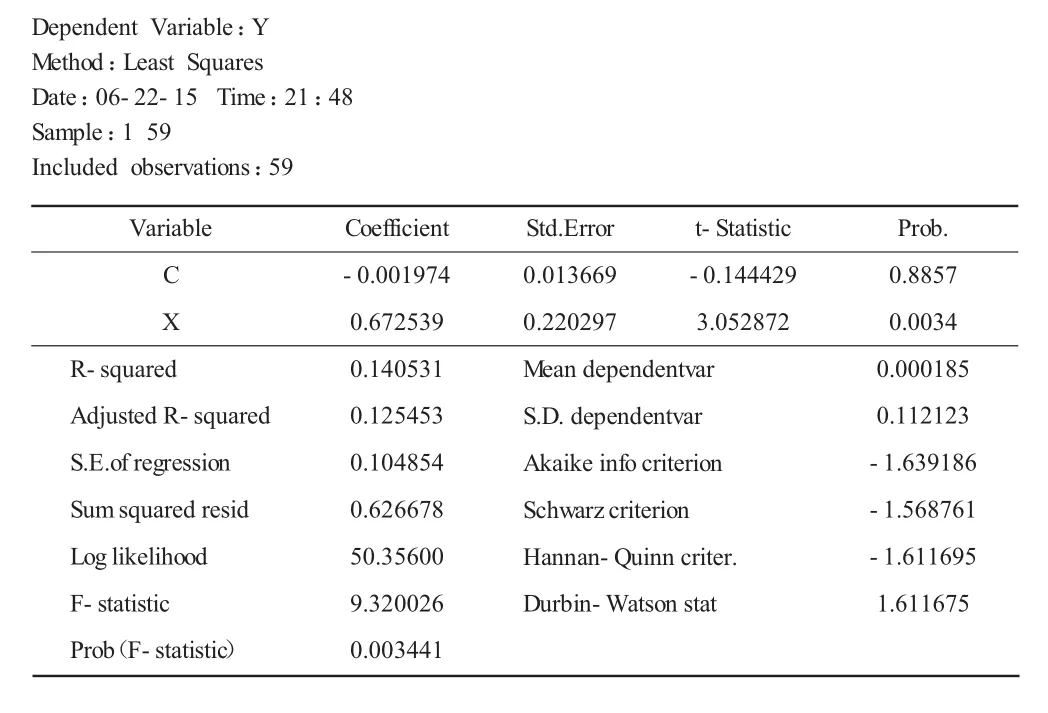
表2 回归结果

五、结论

对系统性风险β系数的准确估计，有助于揭示资本市场的均衡性以及投资者的行为特质，对于资产定价、投资组合的有效管理、交易性金融资产的风险度量意义重大。

本文经过系统的分析，使用时间序列对上海机电股份的β系数进行测算，采用了图形分析和最小二乘法探究上海机电股票市场的预期收益率与其风险之间的关系，预测其β系数，得出以下结论：

（1）上海机电股票的预期收益率与其风险之间存在正的线性关系。根据散点图发现上海机电股份的风险和收益之间存在简单的线性相关性，且为正相关关系。

（2）上海机电股份受市场收益率变化的影响较大。利用最小二乘法，最终计算出上海机电股份的贝塔系数为0.672 539。即：上海机电股份这一风险资产的风险要比整个资本市场当中投资组合的风险要大，相应的其个股收益率也会大于整个资本市场当中投资组合的平均风险收益率。可见上海机电股份受市场收益率变化的影响较大，投资者选择上海机电股份投资还是存在一定的风险。

考虑到本文研究所选择的研究观测值的数量的局限性，本文研究结果的说服力也是非常有限的。因此，在未来的研究中，可以考虑扩大样本数量，使预测结果更加接近现实。

[1]Markowitz.Portfolio Selection[J].Journal of Finance，1952，7：77-91.

[2]Sharpe.Capital asset prices：A theory of market equilibrium under conditions of risk[J].Journal of Finance，1964，19：425-442.

[3]郭艳萍，李娇，2013.资本资产定价模型应用研究——对伊泰股份贝塔系数的测算[J].经济论坛（5）：95-98.

[4]王静.投资者意见分歧与风险——收益权衡关系[D].东北财经大学，2015.

[5]Black F.Capital Market Equilibrium with Restricted Borrowing[J]. Journal of Business，1972，（45）：444-454.

[6]R.Merton.An Intertemporal Capital Asset PricingModel[J].Econometrica，1973，41（5）：867-887.

[7]Ross S.The arbitrage theory[J].Journal of Economic Theory，1976，13：341-360.

[8]王晨曦，2015.资本资产定价模型的缘起、演进与展望[J].智富时代（5）：63-63.

[9]殷俊，李媛媛，2013.基于资本资产定价模型的全国社会保障基金投资组合研究[J].理论与改革（2）：83-84.

[10]Fama Eugene F.，MacBeth James D.Risk，Return and Equilibrium：Empirical Tests[J].Journal of Political Economy，May-June 1973，（81）.

[11]陈梦根，2013.基于混频抽样方法的股市风险-收益关系研究[J].当代财经（11）：47-55.

[12]游宗君，王鹏，石建昌，2010.中国股票市场的收益与波动关系[J].系统管理学报（4）：183-190.

[13]左浩苗，刘振涛，2011.跳跃风险度量及其在风险-收益关系检验中的应用[J].金融研究（10）：170-184.

[14]王天一，刘浩，黄卓，2014.中国股票市场的风险收益关系研究——基于波动率反馈和APARCH-NIG模型的新视角[J].浙江社会科学（10）：16-24.

[15]Andrew Count J.Jennifer Roberts，Mills C.Parameter Stability in the Market Model：Test and Time Varying Parameter Estimation with UK Data[J].The Statistician，1997，46：57-70.

[16]Blume，M.E.On the Assessment of Risk[J].Journal of Finance，1971，26（4）：275-288.

[17]Jagannathan R.，Wang Z.The Conditional CAPMand the Cross-section of Expected Returns[J].The Journal of Finance，1996，51：3-54.

[18]丁志国，苏治，赵晶，2012.资产系统性风险跨期时变的内生性：由理论证明到实证检验[J].中国社会科学（4）：83-102.

[19]简志宏，李彩云.系统性跳跃风险与贝塔系数时变特征[J].中国管理学，2013，21（3）：20-27.

[20]阎志儒.资本资产定价模型的贝塔系数时变性研究[D].西安工业大学，2016.

[21]张矢的.高明宇.吴斌，2014.未充分分散投资下的资本资产定价模型：基于中国 A股市场的实证检验[J].管理评论（10）：24 -37.

[22]陈小先，2014.中国股市动态贝塔系数有效性研究[J].亚太经济（4）：40-45.

（责任编辑：C 校对：T）

F224；F832.51

A

1004-2768（2016）12-0150-04

2016-09-22

张宸（1974-），男，甘肃天水人，兰州理工大学经济管理学院副教授，研究方向：公司理财、会计控制；高芸芸（1991-），女，甘肃高台人，兰州理工大学经济管理学院，研究方向：会计理论、财务会计。