长直管道阀门水击压强变化规律数值模拟研究

李　佳　蒋定国　王　煜

(三峡大学 水利与环境学院， 湖北 宜昌　443002)



长直管道阀门水击压强变化规律数值模拟研究

李佳蒋定国王煜

(三峡大学 水利与环境学院， 湖北 宜昌443002)

摘要：有压管阀门的突然关闭通常伴随水击现象的发生，且不同阀门的关闭对水击的影响也不同．本文利用Fluent软件中的滑移网格技术对3种典型阀门(球阀、蝶阀和闸阀)在突然关闭引起的水击现象进行了三维数值模拟．计算结果表明：各个阀在关阀时间为0.5 s下的最大水击压强要比0.77 s下的高，其中蝶阀的最大水击压强对时间的敏感性相对较低，在一定范围内，通过延长关阀时间来降低水击压强，闸阀和球阀相对于蝶阀而言会更为有效；各阀在关阀时间一定的情况下，碟阀前压强变化相对较缓，其水击压强高峰先于球阀和闸阀出现，且其最大水击压强值要远低于球阀和闸阀，其中闸阀的水击压强最大．在启闭方式和关阀时间一定的情况下，为了减小管路系统遭受水击压强的危害，可优先考虑蝶阀．

关键词：水击；压强；Fluent；滑移网格；阀门

水击作为有压管路中一种重要的水力现象，是以一种压力波的形式沿着管壁传播，使得管壁、阀门或其它管路元件承受极大的动水压力，严重影响了管路系统的正常运行和安全．国内外对水击现象的研究方法主要采用有图解法、解析法和数值方法，其中以数值方法具有计算精度高、方法成熟且适用各类边界条件等多种优点的特征线法得到广泛应用[1-2]．然而，随着计算流体动力学(CFD)不断发展，借助动网格技术不仅实现了阀门动态开关过程中的流动状态和阀体受力情况的模拟，而且还对管道阀门水击过程的压力计算提供了新的方法和技术．沙海飞[3]采用动网格技术对闸门开启过程中的非恒定水流特性进行了数值模拟．刘华坪、陈浮[4]采用动网格技术对管路系统常见的4种典型阀门流场进行了动态数值模拟．华晔[5]、Nikpour[6]分别运用CFX和Fluent软件对管道中的阀门关闭进行了动态模拟，并将计算结果与特征线法及试验进行了对比分析，指出CFD技术可作为计算水击压强的一种方法．郭兰兰[7]运用Fluent软件对球阀变速关闭过程中的水击压强进行了三维数值模拟，分析了关阀时间和关阀方式对水击压强的影响．以上表明，CFD技术在管路水击压强计算的应用中具有可行性．

阀门是一种调节流量和改变压力的调节元件和压力元件，不同阀门具有不同的工作特性，对水流的调节作用不尽相同[8]．因此，有必要针对不同阀门对水击压强的影响进行具体分析．本文在前人的基础上利用滑移网格技术主要对3种典型阀门(球阀、蝶阀和闸阀)在两种不同关阀时间下的水击压强进行了计算，简要地分析关阀时间和阀门型式对水击压强的影响．在一定程度上，可为有压管阀门型式的选择及设计优化提供一些参考．

1研究对象和基本参数

本文采用文献[9]中实验管路为计算模型，针对3种阀门关闭过程所产生的水击现象进行三维动态数值模拟．计算模型的基本参数如图1所示，管道为一水平放置的直管，全段长24.97 m，直径0.1 m，阀芯位置距离管道进口端24.47 m，管道出口端0.5 m．管道进口处为恒定水头，压力水头为2 m，管道出口末端连通大气，表压为0．本文先采用ANSYS前处理软件ICEM CFD对这3种阀门及管道进行了网格划分，考虑到各个模型纵横比较大及计算精度的要求，所有模型都采用六面体结构网格，并对管壁处采用边界层网格进行加密，管道截面及阀门局部处网格如图2所示．网格单元及节点数见表1．

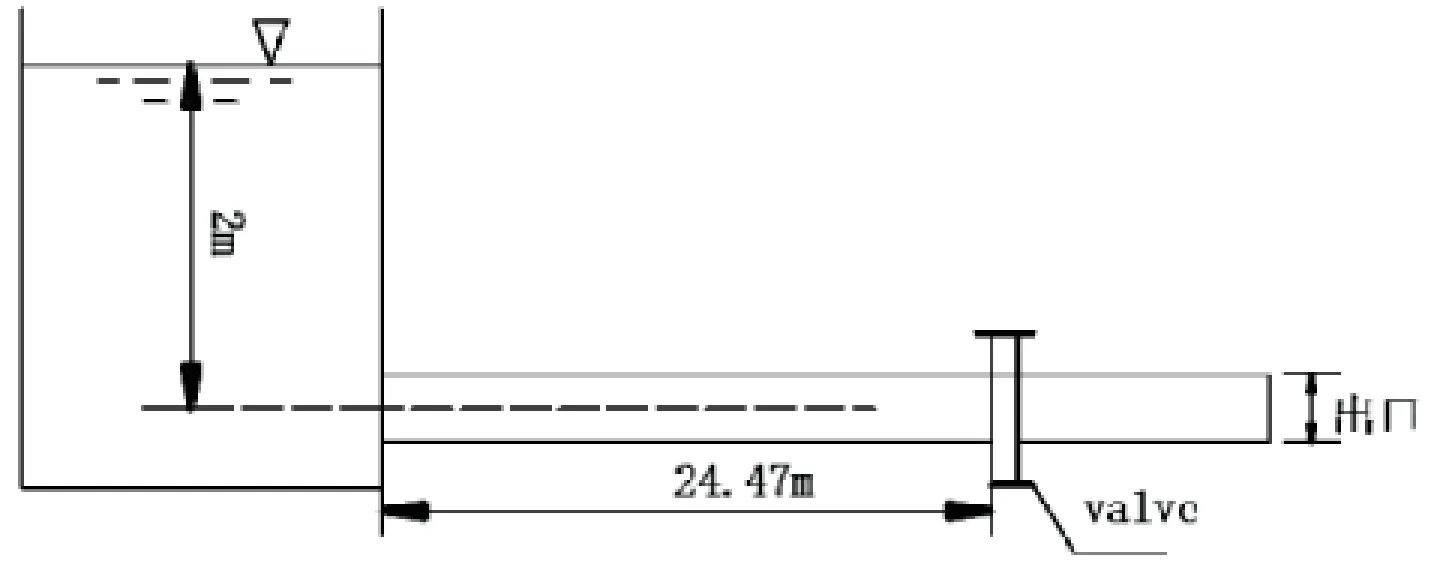
图1　计算模型

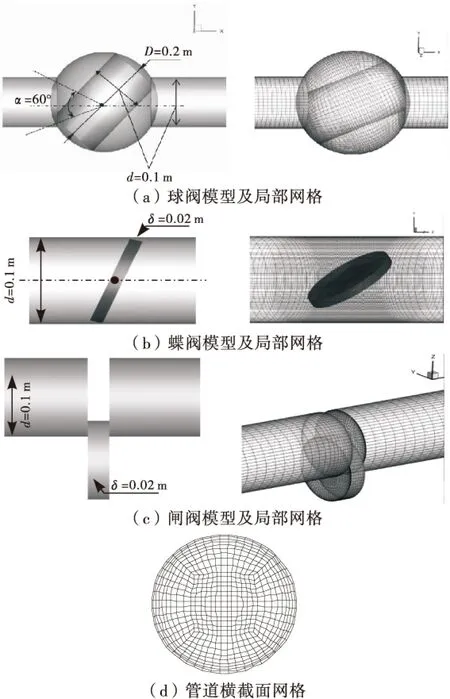
图2　各个阀的模型参数及局部网格

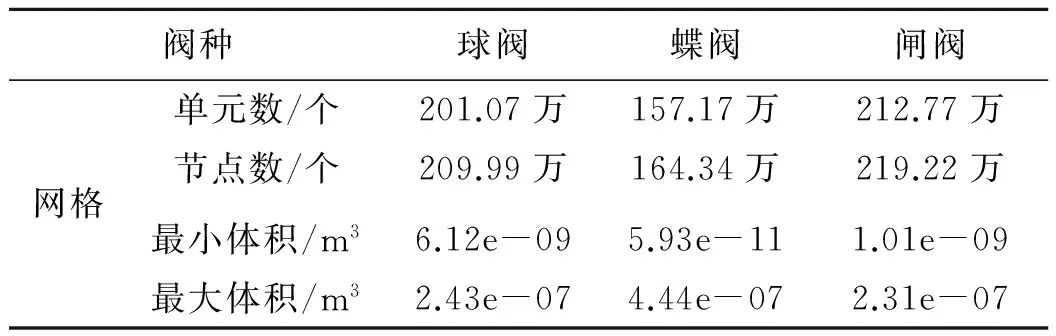
阀种球阀蝶阀闸阀网格单元数/个201.07万157.17万212.77万节点数/个209.99万164.34万219.22万最小体积/m36.12e-095.93e-111.01e-09最大体积/m32.43e-074.44e-072.31e-07

2数值模型及计算方法

2.1流体控制方程

阀门的启闭是一个动态过程，管道中流体呈非定常湍流流动，湍流数值模拟采用标准k-ε两方程模型，流体所遵循的控制方程[10]如下：连续方程

(1)

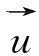
动量守恒方程：

(2)

紊动能方程(k方程)：

(3)

耗散率方程(ε方程)：

(4)

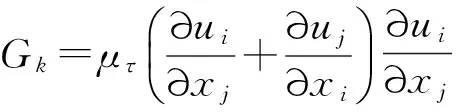
2.2计算方法

各阀芯的运动由滑移网格技术实现．将阀芯与左右管道的接触面分别定义为交界面，即滑移面，自定义函数(UDF)控制阀芯的运动，随着阀芯与滑移面接触面积的缩小直至变为零，实现阀门由全开到完全关闭．其中，闸阀为位移随时间的函数，蝶阀(启闭角90°)和球阀(启闭角60°)采用角速度随时间的函数．为提高计算的收敛性和准确性，每个模型先进行阀门全开的定常计算，然后将计算结果作为瞬态计算的初始值．为研究水击压强随关阀时间的变化关系，设置了两种不同的关阀时间，分别是0.77 s和0.5 s．由于阀门处水击压强最大且持续时间最长，因此取靠近阀门处的管道横截面为监测面，计算出该监测面上所受压强平均值即为最大水击压强．计算时选用耦合压力求解器，二阶迎风格式，PISO瞬态算法，壁面采用无滑移边界，近壁区用标准壁面函数处理．各个模型的计算时间步长为0.002 s，每隔0.02 s自动保存一次计算结果．

2.3计算结果与分析

1)各个阀门在不同关阀时间下的水击压强变化过程分析

图3中a，b和c分别是蝶阀，球阀和闸阀在关阀时间为0.77 s和0.5 s时计算的压强变化曲线．

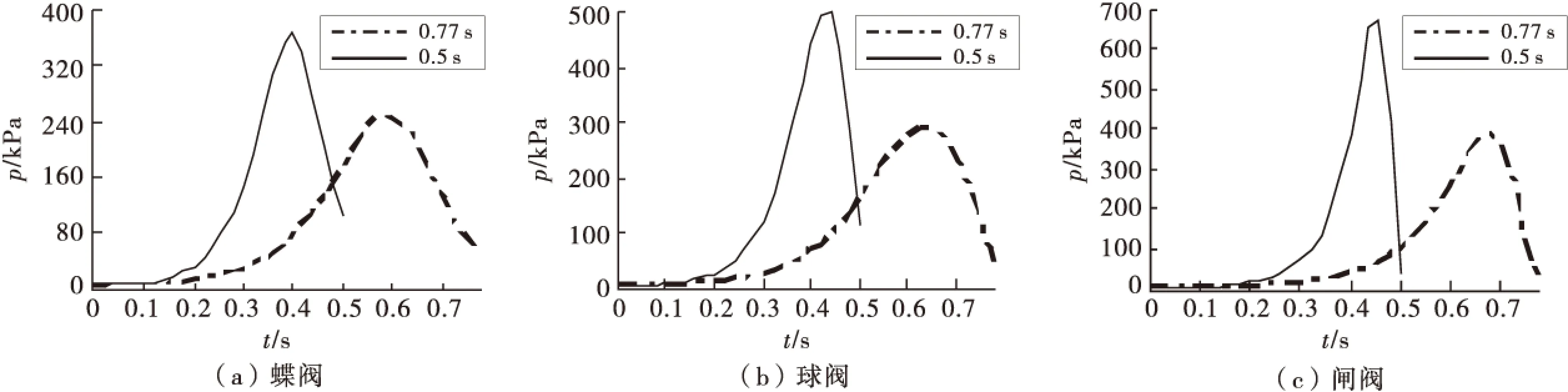
图3　各个阀门在不同关阀时间下水击压强变化曲线

从图3可以看出，在0.5 s关阀时间下的蝶阀、球阀和闸阀出现的最大水击压强都要比0.77 s下的大．显然，以上3种阀门的水击压强随关阀时间都呈相同的变化趋势，说明结果具有普遍性，能反映客观规律，通过延长关阀时间，能有效地降低水击压强．在关阀时间为0.77 s和0.5 s下各阀出现的最大水击压强及时刻见表2，其压力云图如图4所示．从表中所显示的两种关阀时间下的前后最大压强增率上看，闸阀和球阀前后最大压强增率明显高于蝶阀，闸阀的最高．从中可以分析出，闸阀和球阀由突然关阀引起的水击压强对于关阀时间的敏感性要高于碟阀．在一定范围内，通过延长关阀时间来降低出现的最大水击压强大小，闸阀和球阀相对于蝶阀而言会更为有效．

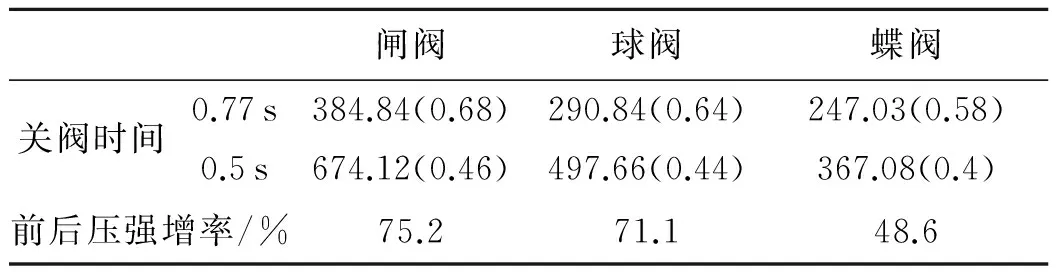
表2　不同关阀时间下出现最大水击压强及其时刻

图4　各个阀的最大压强云图和相应时刻

2)3种阀门在同一关阀时间下的水击压强变化过程分析

图5是3种阀在同一关阀时间(0.77 s或0.5 s)下的压强变化曲线．从图中可以看出，在关阀时间一定的情况下，各个阀出现的水击压强变化曲线有所不同．在关阀时间为0.77 s和0.5 s时，闸阀出现的最大水击压强明显要高于球阀和蝶阀，蝶阀的水击压强最小．出现这种现象的原因主要与阀门处的流场有关．

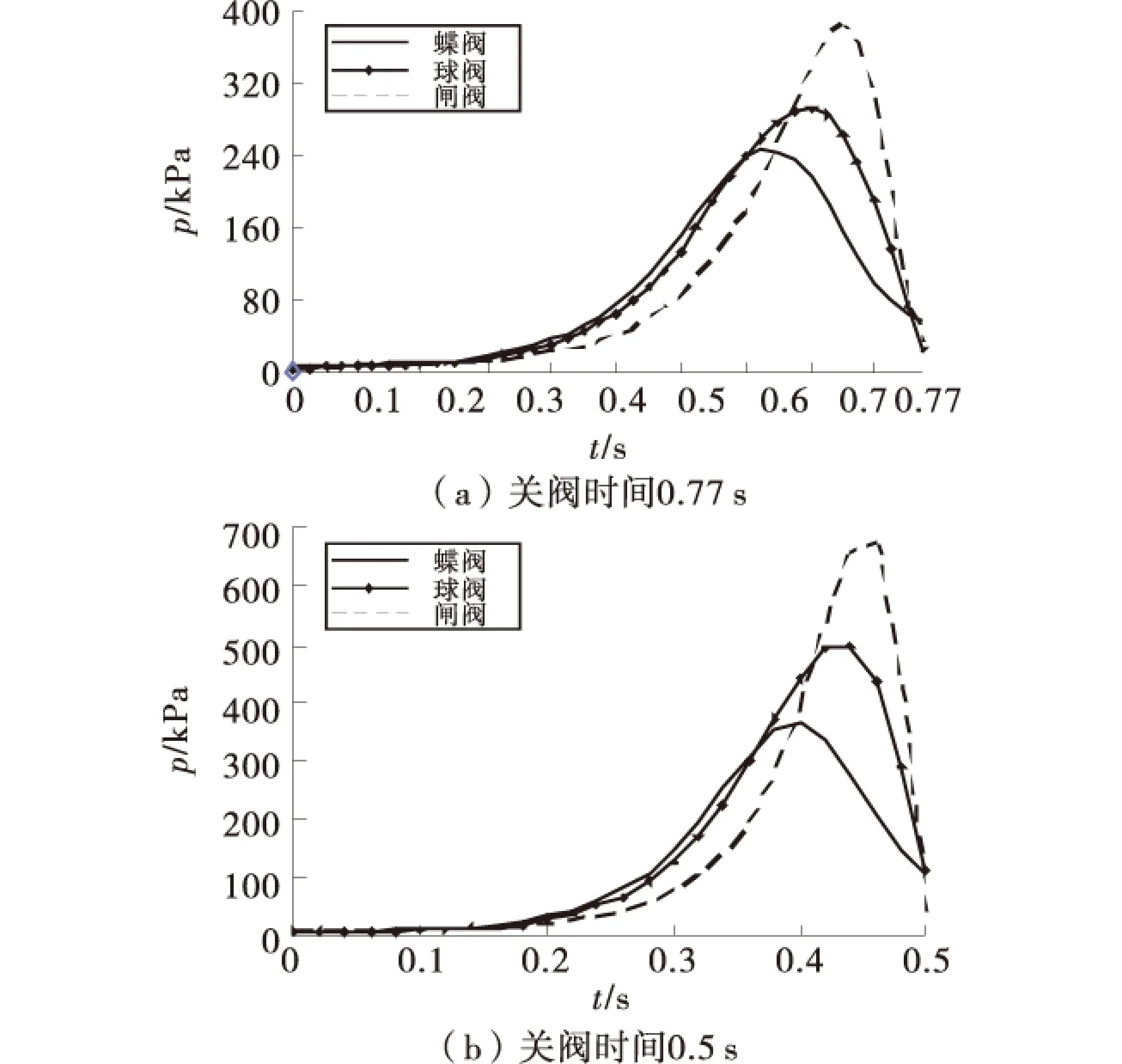
图5　不同关阀时间下各个阀前水击压强的变化曲线

图6是以上3种阀门运动到某时刻下的流线图，从图6可以看出，3种阀门的流线分布差异较大．球阀和闸阀的拐角处出现了漩涡，部分流体被阀体阻隔；蝶阀处没有漩涡，流线被分成两股，以射流的形式从蝶板两端折向下游．这种现象与实际情况非常符合，当任一型式的阀门瞬时关闭时，都会阻碍紧靠阀门处的流体单元流向下游．由于动量突然减小，压强将迅速增大，同时，流体连续性被中断的区域将出现负压状态，这使得阀前后呈现明显的压强差．在压强差的作用下，流体成为高速射流并从阀门与管道的空隙中射向下游，高速射流与低速流体发生剪切，掺混作用，形成漩涡．蝶阀前没有出现漩涡，说明该邻近层的流体单元间流速梯度不大，不足以发生剪切作用产生漩涡，自然水击压强上升的幅度不大．球阀和闸阀前虽有漩涡出现，但是两者的差异在于球阀后的流线随阀门转动有向上折的趋势，缩小了阀上后方的负压区范围；闸阀后的流线则始终以平行于管轴线的方向从阀门下方射出，并未对阀上后方的负压区产生作用．因而，球阀前后压强差没有闸阀的大，当压强差减小时，漩涡强度、范围随之减小，被阻滞的流体也会相应的减少，最终阀体的关阀能力减弱，即阀体受到的水击压强降低．所以，在关阀时间一定的情况下，蝶阀的水击压强就远远低于球阀和闸阀，闸阀最大，球阀次之．从图6(a)和图6(b)可以看出，无论关阀时间为0.77 s还是0.5 s，3种阀门的水击压强变化趋势基本一致，说明计算结果符合普遍规律，可以用来评估水击压强变化规律．为了有效降低水击压强，应优先选用蝶阀作为启闭元件．同时，从图6还可以看出，蝶阀的水击压强波峰出现的时间要先于球阀和闸阀，使得整个管路系统遭受水击危害持续的时间最短，这充分说明了选择蝶阀来降低水击压强具有相当大的优势．

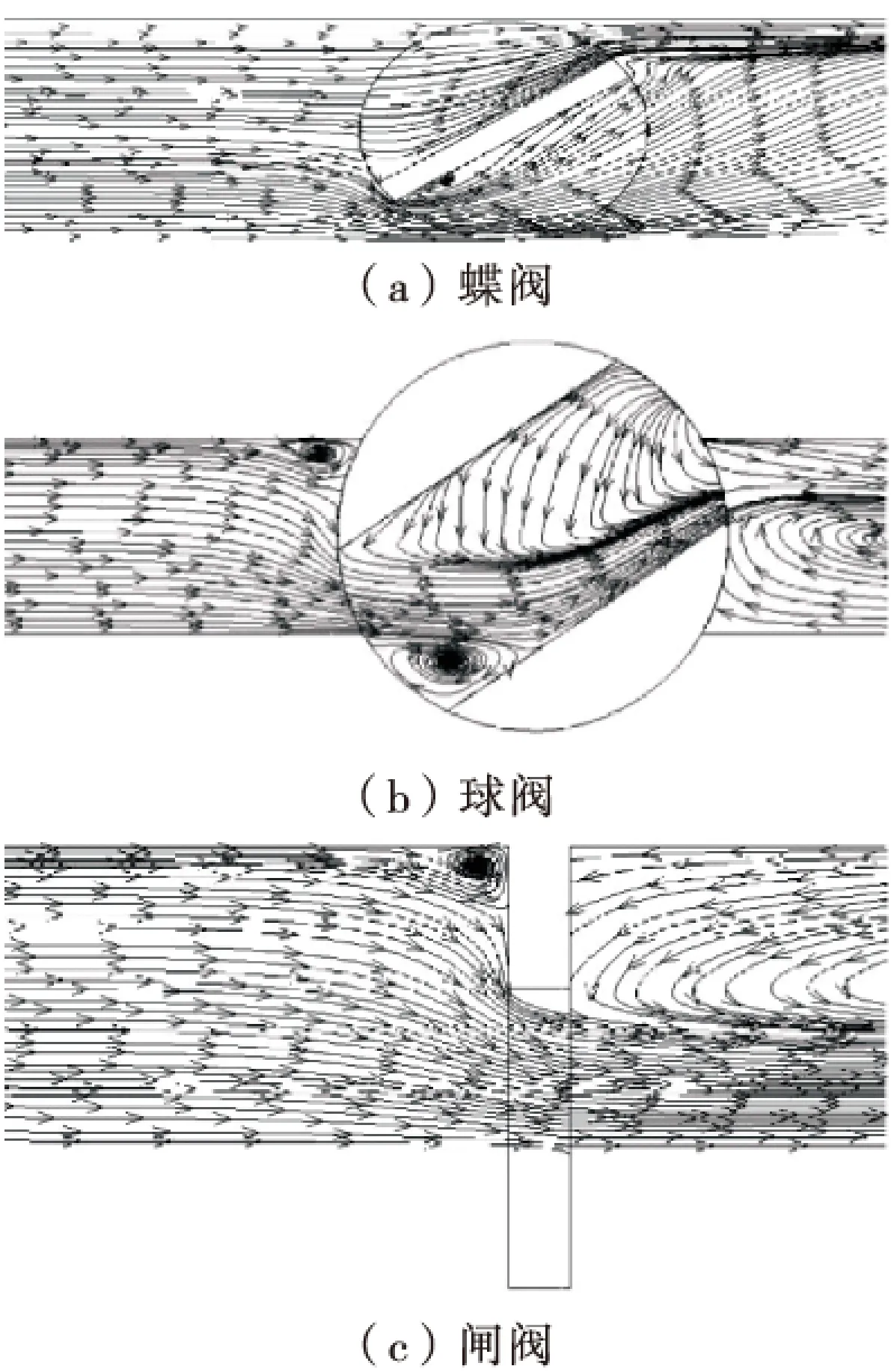
图6　3种阀门某瞬时流线图

3结论

本文利用CFD技术对管路系统中的3种典型阀门的水击压强进行了三维数值模拟，通过对3种阀门压强变化过程的对比，分析了不同阀门型式和关阀时间对水击压强的影响．结果表明：1)不同关阀时间下，各个阀在关阀时间为0.5 s下的最大水击压强要比0.77 s下的高，且闸阀和球阀的最大

水击压强增率显著高于蝶阀，说明蝶阀的最大水击压强对时间的敏感性相对较低，在一定范围内，通过延长关阀时间来降低水击压强大小，闸阀和球阀相对于蝶阀而言会更为有效；2)在关阀时间一定的情况下，蝶阀的最大水击压强要低于球阀和闸阀，闸阀最大，球阀次之．同时，蝶阀的水击压强波峰出现的时间要先于球阀和闸阀，使得整个管路系统遭受水击危害持续的时间最短．由于各个阀门在关阀时间为0.77 s或0.5 s时，产生的水击压强变化趋势基本一致，说明计算结果符合普遍规律，可以用来评估水击压强变化规律．因此，在启闭方式和关阀时间一定的情况下，为了降低管路系统遭受水击压强的危害程度，可优先考虑蝶阀作为管路系统的启闭元件．

参考文献：

[1]朱永忠，索丽生，张健．简单管水力系统水击的级数解析解[J]．河海大学学报：自然科学版，2007(5)：577-580．

[2]HIMR D． Numerical Simulation of Water Hammer in Low Pressurized Pipe： Comparison of Simhydraulics and Lax-Wendroff Method with Experiment[C]． Ostrava： Czech Republic， 2013．

[3]沙海飞，周辉，吴时强，等．用动网格模拟闸门开启过程非恒定水流特性[A]．中国水利学会．中国水利学会第二届青年科技论坛论文集[C]．中国水利学会，2005：6．

[4]刘华坪，陈浮，马波．基于动网格与UDF技术的阀门流场数值模拟[J]．汽轮机技术，2008(2)：106-108．

[5]华晔，廖伟丽．CFD技术在管道阀门水击计算中的应用[J]．电网与清洁能源，2009(3)：72-75．

[6]Nikpour M R, Nazemi A H, A． Hosseinzadeh Dalir, et al． Experimental and Numerical Simulation of Water Hammer[J]． Arabian Journal for Science and Engineering, 2014：394．

[7]Guo L, et al, Study of the Phenomenon of Water Hammer Based on Sliding Mesh Method, in Development of Industrial Manufacturing, S.B. Choi, F.S. Hamid, and L. Han, Editors， 2014：236-239．

[8]汤跃，汤玲迪，刘二会，等．闸阀调节过程的三维模拟及其动态模型[J]．排灌机械工程学报，2012(2)：219-224．

[9]倪昊煜，杨玲霞，吴建平，等．水击计算与方程的实验验证[J]．河南科学，2004(4)：505-507．

[10] 王福军．计算流体动力学分析-CFD软件原理与应用[M]．北京：清华大学出版社，2004：7-9．

[责任编辑周文凯]

收稿日期：2015-12-21

基金项目：国家自然科学基金资助项目(51409151)；三峡大学人才科研启动基金资助项目(KJ2012B031)

通信作者：蒋定国(1980-)，男，副教授，博士研究生，研究方向为计算流体力学．E-mail：jiangdingguo@aliyun.com

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.002

中图分类号：TV137

文献标识码：A

文章编号：1672-948X(2016)02-0007-04

Numerical Simulation of Change Rule of Water Hammer Pressure of a Long Straight Pipe Valve

Li JiaJiang DingguoWang Yu

(College of Hydraulic & Environmental Engineering, China Three Gorges Univ., Yichang 443002, China)

AbstractSudden closing of the pressure pipe valve is usually accompanied by the occurrence of water hammer phenomenon; the impacts of different valves close on water hammer are also different. In this paper, the three-dimensional numerical simulation of the water hammer phenomenon caused by the sudden closure of three kinds of typical valves (ball valve, butterfly valve and gate valve) is carried out by using the sliding grid technology of Fluent software. The water hammer pressures of these three typical valves are calculated. The results show that the maximum water hammer pressure of the valve under closing time of 0.5s is higher than that of 0.77s; the maximum water hammer pressure of butterfly valve has a relatively low sensitivity to time; in a certain range, by extending the valve closure time to reduce the size of the water hammer pressure, the gate valve and ball valve relative to the butterfly valve are more effective. At the same time, when the valve closing at a certain time, the pressure change at the butterfly valve is relatively slow; and its water hammer pressure peak was ahead of ball valve and gate valve appeared; the maximum water hammer pressure of the butterfly value is lower than that of the ball valve and gate valve; and the maximum water hammer pressure of the gate valve is the highest. When the valve closing mode and closing time are fixed, in order to reduce the risk of water hammer pressure in the pipeline system, the butterfly valve has priority over other valves.

Keywordswater hammer;pressure;Fluent;sliding mesh;valve