混凝土细观模拟的不同建模技术影响分析
2016-08-01叶永余欢罗威卢强
叶 永 余 欢 罗 威 卢 强
(三峡大学 水利与环境学院, 湖北 宜昌 443002)
混凝土细观模拟的不同建模技术影响分析
叶永余欢罗威卢强
(三峡大学 水利与环境学院, 湖北 宜昌443002)
摘要:建立了圆形、正多边形、随机多边形3种不同形状骨料的150 mm×150 mm随机骨料模型,且将随机多边形骨料模型单元等效均质化后得到细观单元等效化模型,进行4种不同随机模型的影响分析.结果表明:随机多边形骨料模型的计算精度最高,正多边形骨料模型次之,且4种模型与试验结果的误差均在7%以内;随机骨料模型中,细观单元等效化模型运算效率较高,且能保证一定的计算精度.
关键词:混凝土;细观模拟;等效均质化;建模技术;运算效率
0引言
从细观的角度,一般将混凝土材料视作由骨料、砂浆和界面等多相材料构成.在混凝土的制备过程中,骨料构成了混凝土材料的骨架,对混凝土材料的力学性能具有显著的影响,研究表明骨料对混凝土各项力学性能均具有决定性的作用[1].所以从细观角度研究骨料形状及其在砂浆中的分布对混凝土材料力学性能的影响具有重要的意义.
为模拟混凝土不同的骨料形状,众多学者进行了探讨,如进行二维混凝土模拟时骨料常采用圆或椭圆近似模拟[2],对于三维混凝土骨料常采用圆球或椭球等简单形状近似模拟[3],在此基础上进一步提出了多边形乃至任意形状混凝土骨料的模拟[4].然而随着混凝土骨料形状的模拟越来越接近真实骨料形状,在提高计算精度的同时带来了另外一个研究难点——计算效率问题.骨料的不断细致化,划分的网格数量越来越多,导致计算的时间愈长,运行效率愈低,不利于研究的进行.为提高运行效率,杜修力等基于复合材料力学均质等效化理论提出了混凝土细观单元等效化力学模型[5],该模型增加了网格单元尺寸,使网格数量大大减少,节省了计算资源,提高了运算效率.
分别选用圆形骨料、正多边形(八边形)骨料、随机多边形骨料,建立平面二维混凝土细观随机骨料模型,并根据均质等效化理论将随机多边形骨料模型进行单元等效均质处理,建立细观单元等效化模型.以混凝土单轴拉伸试验为例进行模拟,并与实际试验结果进行对比,分析不同模型的计算结果误差大小,并比较4种模型的计算时间,分析模型的计算效率.
1建模技术
1.1随机骨料模型
按照富勒的理想最大密实度级配曲线计算的各粒径骨料级配,可以制备得到结构布局最合理和强度最大的混凝土.混凝土试件的横截尺寸为150 mm×150 mm,然后按照二级配骨料计算,小石∶中石为0.45∶0.55.模拟计算试件为二维平面结构,根据学者Walraven提出的富勒级配曲线的三维向二维的转换公式:
(1)
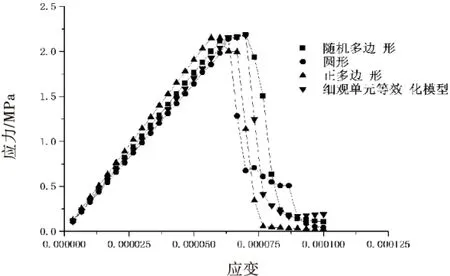
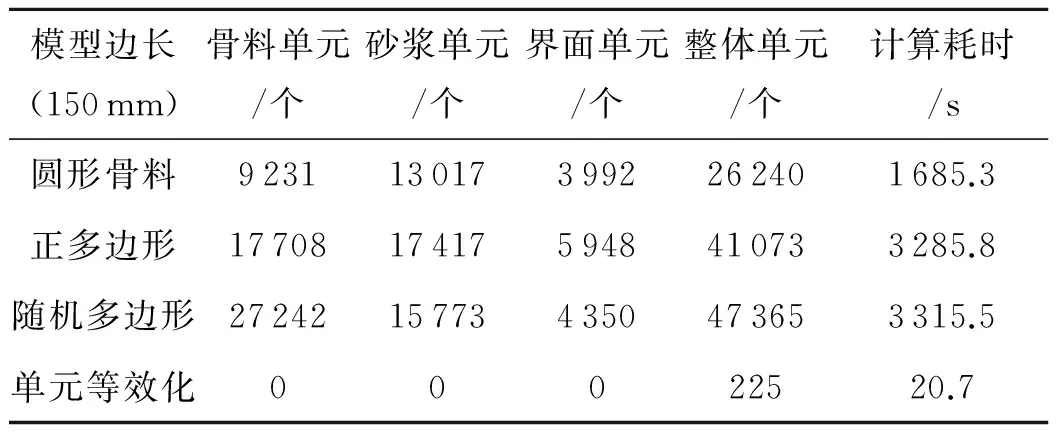
式中,PC(D 骨料投放按照以下步骤: Step1:由式(1)计算二级配骨料的半径与数量,在给定的150 mm×150 mm投放空间内,利用Monte Carlo法随机生成骨料的坐标. Step2:判断骨料是否合格,如果新生成骨料与原有骨料相交则重新生成骨料. Step3:判断生成骨料的数量是否满足该级配要求,若满足要求则生成下一级配骨料,否则继续生成相关骨料. Step4:在已有的圆形骨料基础上内接多个顶点,逆时针连接各顶点即可得到正多边形骨料和随机多边形骨料,计算内接多边形的面积,然后再重新生成骨料,直到满足级配要求. 由Step1~Step3即可得到圆形骨料随机模型,通过Step4计算多边形的顶点坐标,即可得到正多边形骨料模型和随机多边形模型. 1.2细观单元等效化模型 杜修力[6]认为细观力学模拟是通过考虑细观层次多相材料之间的相互影响来研究复合材料的宏观力学性能.复合材料的非均匀性从本质上导致了复合材料力学行为的非线性,因此只要抓住材料非均匀性这个本质特征就可以确定材料宏观力学特性.基于此,提出了细观单元等效化模型:Voigt并联模型,并采用复合材料力学的等效方法推导了单元等效化后各单元的等效力学参数.经过多次模拟计算,10 mm×10 mm的网格划分方案能够得到稳定数值解且误差在允许范围内. 2算例分析 2.14种模型的建立 根据水工混凝土试验规程[7],二级配混凝土标准试件尺寸为150 mm×150 mm×150 mm,骨料最大粒径为40 mm.采用Monte Carlo法依照上文所述步骤,建立二维随机骨料模型试件,分别向试件投放3种不同形状的随机骨料,生成相应的细观模型,如图1(a)~(c)所示.试件中不同粒径骨料比重:代表中石骨料(直径d=20~40 mm)的面积比为25%,小石骨料(d=5~20 mm)的面积比为20%.再根据单元等效化方法将随机多边形骨料模型进行等效均质得到细观单元等效化模型,如图1(d)所示,计算各单元的等效力学参数. 图1 随机骨料模型与细观单元等效化模型 材料力学参数,骨料弹性模量E=60 GPa,泊松比ν=0.167,抗拉强度σ0=10 MPa;砂浆弹性模量E=22 GPa,泊松比ν=0.22,抗拉强度σ0=3.5 MPa;界面弹性模量E=15.4 GPa,泊松比ν=0.22,抗拉强度σ0=1.75 MPa. 2.2混凝土单轴拉伸模拟 本算例利用有限元软件ANSYS进行计算,模型中各相材料视为弹脆性,本构关系如图2所示,选取最大拉应变准则作为混凝土单元拉伸失效的破坏准则,即单元最大拉应变超过阈值则认为单元破坏,通过修改其刚度矩阵实现强度折减;未超过其阈值时为弹性阶段,不发生破坏.在4种混凝土试件模型中,试件底部施加全约束;两侧为自由边界,无约束作用;上部边界施加载荷.荷载施加采用的是位移加载控制,逐级加载步长0.005 mm. 图2 弹脆性本构示意图 图3是单轴拉伸条件下,利用4种模型分别计算获得的混凝土试件的应力-应变关系曲线图.可以看出,利用4种模型对混凝土试件进行分析,得到的应力应变曲线均具有完整的上升段、峰值点以及刚度退化对应的下降段,能够完整的模拟出单轴拉伸试验中混凝土试件的应力-应变变化情况. 图3 不同模型应力应变曲线图 2.3抗拉强度计算 采用4种模型得到混凝土抗拉强度分别为2.16 MPa(圆形)、2.17 MPa(正多边形形)、2.18 MPa(随机多边形)、2.15 MPa(细观单元等效化模型),与试验结果[8]相比,吻合效果较好,见表1. 表1 4种模型计算值与试验值的误差 可以看出,4种模型的计算值与试验值的误差均较小,都未超过10%,其中随机多边形骨料模型的误差最小,正多边形骨料模型次之.3种不同形状骨料模型的计算精度排序:随机多边形>正多边形>圆形,与预期结果相符.细观单元等效划模型相对随机多边形骨料模型误差有所增大,但也未超过7%,说明细观单元等效化模型在提高运算效率的同时也保证了计算结果的可靠性与准确性. 2.4运算效率分析 通常在混凝土细观力学模型中,为使模型得到稳定的宏观力学特性,其网格剖分尺寸需不大于骨料最小颗粒粒径的1/4[9-10],即在二级配混凝土平面模型算例中将至少采用2 500个单元(50×50)才能获得稳定解.本文中采用的4种模型的网格数和计算耗时对比见表2. 表2 计算量对比 由表2可知,圆形骨料模型,正多边形模型和随机多边形模型采用传统的网格划分方法,单元数巨大,每一次计算耗时较多,运算效率较低.相比于前3种模型,细观单元等效化模型的单元数量极少,单元自由度数大大减小,每次计算时间都只有数十秒,运算效率极高,且计算结果能保证有一定的精度,适合重复多次计算.针对二维细观模型,采用普通网格划分方法模型的单元数已有数万,计算一次需要近30 min.若推广到三维细观模型,采用传统的网格划分方法单元数将极大增加,运算效率更为低下,不利于研究进展.若采用细观单元等效化模型的网格划分方法,即便在三维模型的情况下,单元数也只有3 375个,运算效率极高,其优越性非常明显. 3结论 1)采用相同的骨料粒径和骨料比重,对3种不同骨料形状的混凝土试件模型进行断裂过程的数值模拟,结果表明,不同骨料形状的混凝土试件在单轴拉伸时的应力峰值不同,但差别很小,与试验值对比,误差在允许的范围内.3种不同形状骨料模型的计算精度:随机多边形>正多边形>圆形,表明骨料形状的细致化越接近真实情况,计算结果的精度越高. 2)对比传统细观力学网格划分方法,细观单元等效化模型网格数量大大减小,模型的运算效率也随之大大提高,且能够保证一定的准确性.在运算速度上具有极大的优越性,可以进一步推广到三维立体模型中. 参考文献: [1]潘子超,阮欣,陈艾荣.基于任意级配的二维随机骨料生成方法[J].同济大学学报:自然科学版,2013,41(5):759-764. [2]Bazant Z P, Tabbara M R. Random Particle Models for Fracture of Aggregate or Fiber Composites[J]. Journal of Engineering Mechanics, ASCE, 1990,116(8):1686-1705. [3]李运成,马怀发,陈厚群,等.混凝土随机凸多面体骨料模型生成及细观有限元剖分[J].水利学报,2006,37(5):588-592. [4]杜成斌,孙立国.任意形状混凝土骨料的数值模拟及其应用[J].水利学报,2006,37(6):662-667. [5]杜修力,金浏.基于随机多尺度力学模型的混凝土力学特性研究[J].工程力学,2012,28(1):151-155. [6]杜修力,金浏.混凝土材料宏观力学特性分析的细观单元等效化模型[J].计算力学学报,2012,29(5):654-661. [7]SL352-2006,水工混凝土试验规程[S].2006. [8]杨木秋,林泓.混凝土单轴受压受拉应力-应变全曲线的试验研究[J].水利学报,1992,23(6):60-66. [9]彭一江,黎保琨,刘斌.碾压混凝土细观结构力学性能的数值模拟[J].水利学报,2001,32(6):19-22. [10] 马怀发,陈厚群,黎保琨.混凝土试件细观结构的数值模拟[J].水利学报,2004,35(10):27-35. [责任编辑周文凯] 收稿日期:2016-01-19 基金项目:国家自然科学基金项目(编号:11302119) 通信作者:叶永(1969-),男,教授,博士,主要从事固体力学研究.E-mail:yyeeong@yahoo.com.cn DOI:10.13393/j.cnki.issn.1672-948X.2016.02.008 中图分类号:TV43 文献标识码:A 文章编号:1672-948X(2016)02-0033-04 Analysis of Impact of Different Modeling Techniques on Concrete Mesoscopic Simulation Ye YongYu HuanLuo WeiLu Qiang (College of Hydraulic & Environmental Engineering, China Three Gorges Univ., Yichang 443002, China) AbstractA 150mm×150mm random aggregate model with three different shapes aggregates of circular, regular polygon and random polygon is established; and the micro-unit equivalent model is established by the equivalent homogenization of random polygon aggregate model unit; and then the influences of four different stochastic models are analyzed. The results show that the accuracy of the random polygon aggregate model is the highest; the regular polygon aggregate model followed; and the errors of the four models with the experimental results are within 7%; in the random aggregate models, the micro-unit equivalent model has higher computational efficiency, so as to ensure the certain degree of accuracy. Keywordsconcrete; mesoscopic simulation; equivalent homogenization; modeling techniques; computational efficiency