基于蒙特卡罗法的库岸滑坡可靠度分析——以三峡库区某滑坡为例

闫国强　易　武　邓永煌　柳　青　黄海峰

(1. 三峡大学 土木与建筑学院， 湖北 宜昌　443002； 2. 三峡大学 三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌　443002； 3. 湖北长江三峡滑坡国家野外科学观测研究站， 湖北 宜昌　443002； 4. 三峡大学 科技学院， 湖北 宜昌　443002)



基于蒙特卡罗法的库岸滑坡可靠度分析
——以三峡库区某滑坡为例

闫国强1，2，3易武1，2，3邓永煌4柳青1，2，3黄海峰1，2，3

(1. 三峡大学 土木与建筑学院， 湖北 宜昌443002； 2. 三峡大学 三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌443002； 3. 湖北长江三峡滑坡国家野外科学观测研究站， 湖北 宜昌443002； 4. 三峡大学 科技学院， 湖北 宜昌443002)

摘要：本文基于蒙特卡罗随机抽样算法，进行3 000次模拟抽样对三峡库区某库岸滑坡进行两种工况下稳定性对比分析．结果表明：考虑了175 m库水及孔隙水压力的工况2较工况1稳定系数均值，可靠度指标均减小，失效概率增大，最不利组合稳定系数相差不大，最优组合稳定系数相差较大；滑体重度与稳定系数呈现微弱负相关，滑体的粘聚力和内摩擦角与稳定系数呈正相关，且内摩擦角的相关性远大于粘聚力，滑床各参数与稳定系数相关性为0；工况2与1相比，重度、内摩擦角与稳定系数的相关性减弱，粘聚力与稳定系数的相关性增强．

关键词：蒙特卡罗法；可靠度分析；三峡库区；滑坡

滑坡是一种常见的地质灾害，随着人类的发展，滑坡对人类的生命财产破坏性也越来越大．因此对于滑坡稳定性的研究一直是困扰工程界学术界的热门话题[1-3]．目前，对滑坡稳定性的计算一般有如下几种方法：以极限平衡为主的传统算法、有限元模拟方法[4-6]以及现今发展的非线性、数字信息技术的新技术方法．传统的不同算法，虽然各自的假设条件和应用范围有所不同，但是它们大多都是以滑坡岩土体确定的强度参数为基础进行稳定性计算的．不幸的是，作为大型滑坡岩土体物理参数具有不均一性、空间变异性，而这都与模拟计算采取的确定的岩土体参数不一致，这也往往造成了计算出看似很“安全、可靠”的稳定系数，但也仍然不乏发生滑坡灾害的工程实例[7]．因此基于概率敏感性计算的可靠度理论成为滑坡稳定计算的一种趋势．可靠度理论考虑了滑坡岩土体本身的复杂性和不确定性，如岩土体参数粘聚力c，内摩擦角Φ，重度γ的离散型和不确定性．相较于传统的确定单一的稳定系数法，通过稳定系数、可靠度指标、失效概率、各参数敏感性等对滑坡进行综合分析评价，更加符合工程实际[8]．本文以三峡库区某库岸滑坡为例，基于蒙特卡罗随机抽样法进行可靠度分析，同时耦合Seep、Slope模块，按照是否考虑库水及孔隙水压力作用划分两种不同的工况．对两种工况的可靠度、稳定系数等进行对比分析，以期揭示库水及空隙水压力对滑坡稳定性的影响，

最后对滑坡岩土体各物理力学参数进行敏感性分析，以期研究岩土体各参数对滑坡稳定性的相关性．

1滑坡地质背景

滑坡位于长江左岸，距三峡大坝48.2 km．滑坡为斜逆向陡坡，地貌上为一典型的长条圈椅状凹槽地形，中下部为坡型较缓的平台，上部为圈椅状较陡斜坡．滑体纵长800 m，平均宽约260 m，前缘高程80 m，后缘高程390 m．滑体面积约20.8×104m2，滑体均厚约30 m，滑体规模约624×104m3(如图1所示)．

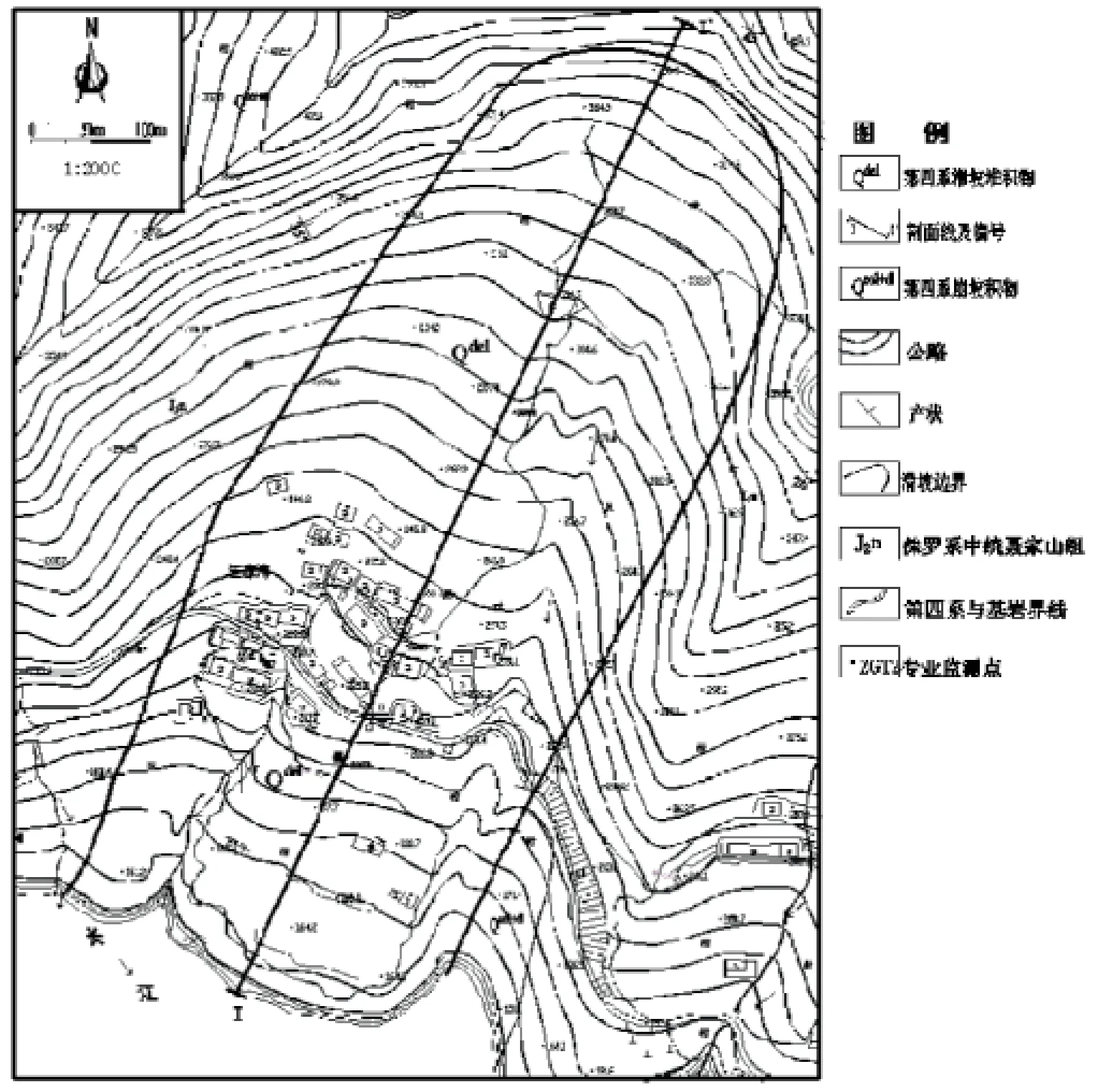
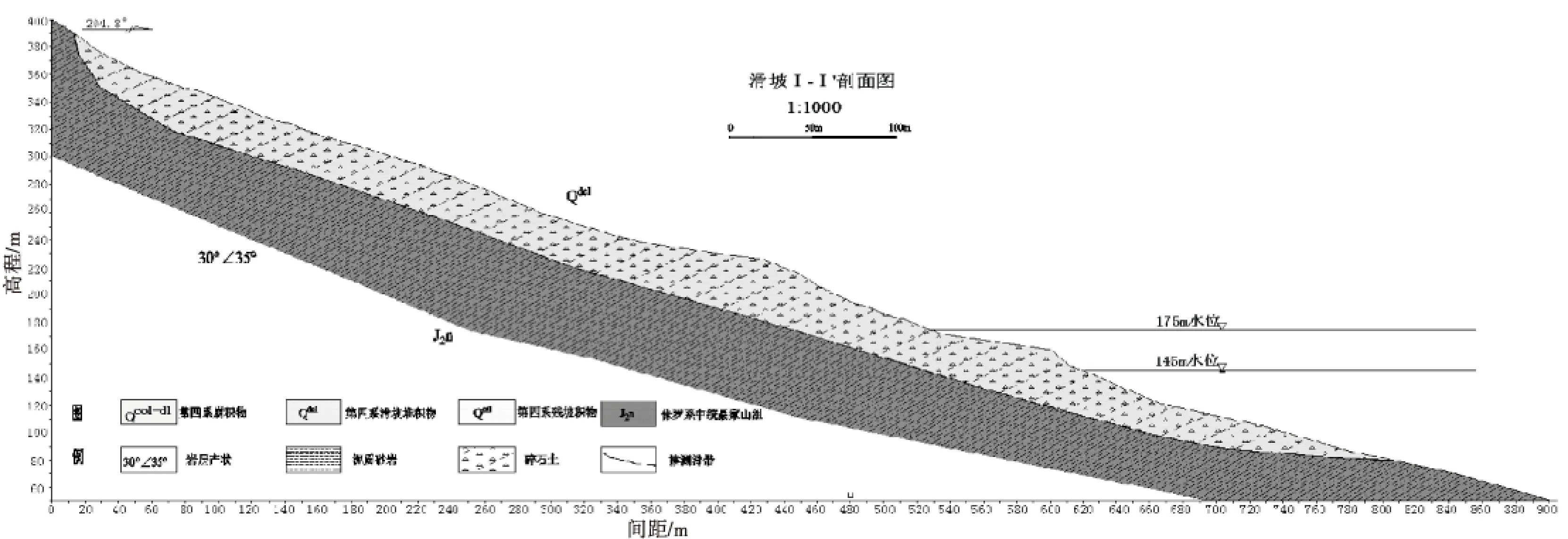
图1　滑坡平面图及1-1剖面图

滑坡体物质主要由第四纪崩坡积物构成，为砂岩块石、碎石土及粉质粘土堆积层．滑带为堆积层与基岩的接触带，以碎石土及软弱粉质土为主，为隔水层．滑床为向坡体内倾的逆向侏罗纪砂泥岩层，岩层产状：30°∠35°．

2基本原理及模型建立

2.1可靠度分析基本原理

岩土体参数一般符合正态分布，基于此，设计蒙特卡罗抽样实验时，滑坡岩土体的物理参数粘聚力c，内摩擦角Φ，重度γ都服从式(1)：

(1)

其中，x为变量(c、Φ、γ)；μ为相对应变量的均值；σ为标准差．计算稳定系数时，从岩土体物理参数对应的式子中，分别进行随机抽样，然后运用同时考虑力及力矩平衡的morgenstern price(M-P)算法，计算出其稳定性．在滑坡失稳概率及可靠度计算研究中，一般对c、φ、γ抽样1 000次即可满足可信度80%的要求[9]．本文采用3 000次的抽样．此时可求得3 000个稳定系数F的样本值，从而得出随机变量F的分布，经统计即可得F<1.0的概率，则破坏概率为

(2)

其中，NI为F小于1的抽样次数；N为抽样模拟的总次数．研究表明稳定性系数F通常服从正态分布．若用β表示可靠性指标，将其标准化后则可定义为：

(3)

其中，μF为稳定系数均值；σF为稳定系数分布函数的标准差．则滑坡失效概率为：

(4)

其中，φ(β)为标准正态分布函数，则由数理统计知识不难看出，可靠指标β越大，φ(β)值也就越大，则滑坡的稳定状况越好，滑坡失效概率PF越小，滑坡越不易失稳．反之，可靠指标β越小，φ(β)值也就越小，则

滑坡的稳定状况越差，滑坡失效概率PF越大，滑坡越易失稳．

2.2模型建立

综合运用Geostudio中的Seep、Slope两个模块并结合Slope中蒙特卡罗随机抽样法对滑坡进行可靠度分析．Slope进行稳定性计算时，采用M-P算法，考虑拉裂缝的影响，采用完全指定滑面同时对滑面进行优化计算．建立滑坡地质模型如图2所示，网格划分为5 219个节点，5 113个单元．

图2　滑坡地质模型

2.3模型材料物理属性

岩土体物理力学参数符合正态分布曲线，结合野外剪切试验、室内直剪试验、地质类比及反演分析等方法综合取值，该滑坡体的物理力学参数见表1．其中滑体、滑床的物理力学参数：重度γ，粘聚力c，内摩擦角Φ的正态分布曲线如图3～4所示．

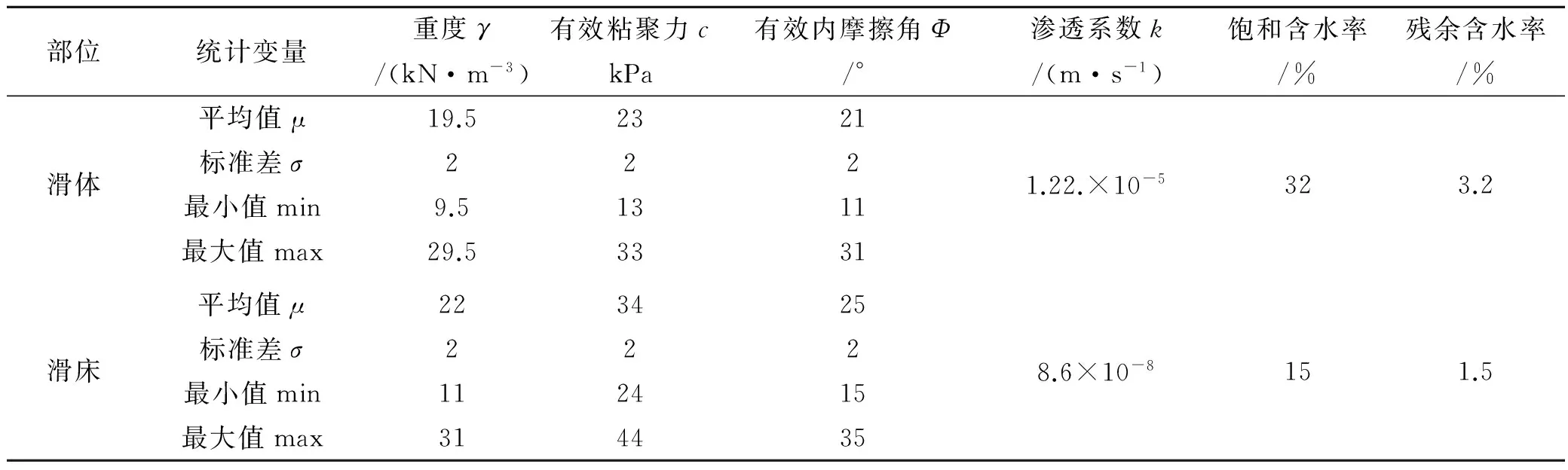
表1　滑坡土体物理力学参数表

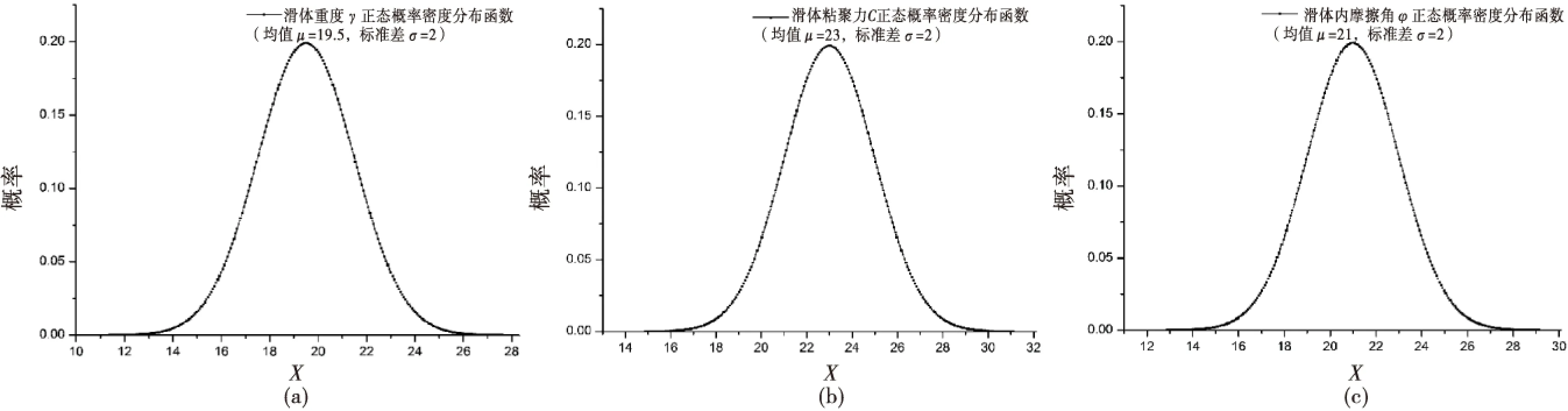
图3　滑体γ、c、Φ正态概率密度分布函数

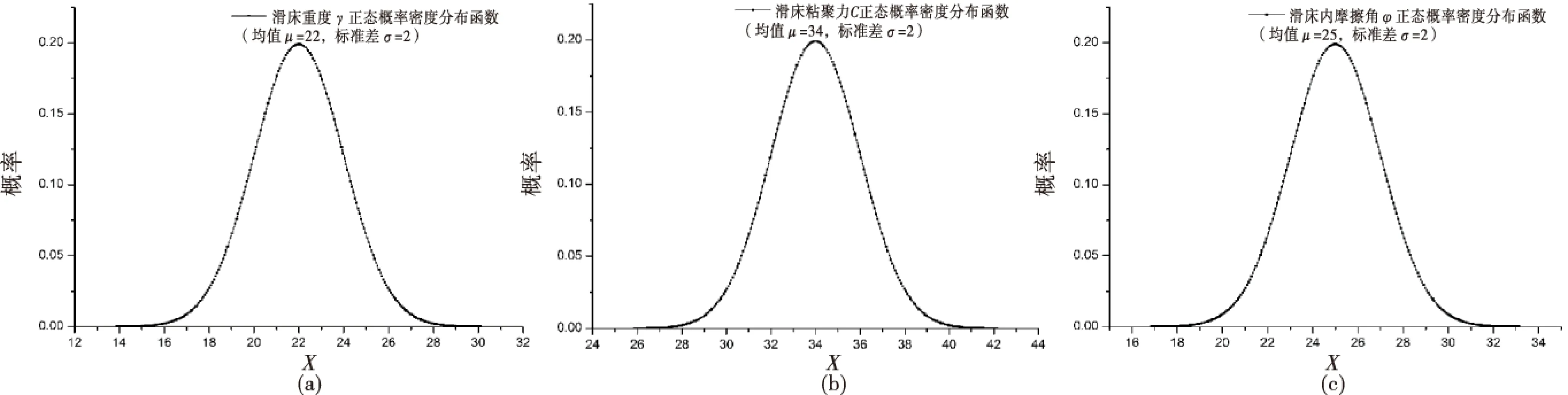
图4　滑床γ、c、Φ正态概率密度分布函数

3可靠度分析及敏感性分析

本文主要设计了两种工况，工况1是不考虑库水及孔隙水压力作用，岩土体强度参数按照正态分布，基于蒙特卡罗随机抽样模拟方法，计算滑坡本身的稳定系数、可靠度指标、失效概率等．同时将岩土体各物理力学参数按照均匀分布进行敏感性分析，计算岩土体各参数与滑坡稳定系数的相关性．工况2则是考虑了库水及孔隙水压力作用，剩下计算步骤同工况1，值得注意的是，本文联合运用Seep和Slope来考虑库水位及孔隙水压力的作用，库水位选择最高水位175 m，同时Slope中采用M-P极限平衡算法，考虑拉裂缝的影响，完全指定滑面同时沿滑面考虑优化计算．在敏感性分析中，为了便于统一叙述，将滑体、滑床的岩土体物理力学参数重度γ，粘聚力c，内摩擦角Φ，统一归化为0-1的区间内，0代表最小值，1代表最大值，以本文工况1滑体的内摩擦角Φ为例，0代表Φ为22.5°，1代表Φ为27.5°，Φ在22.5～27.5°均匀分布，组中值为25°，以每隔0.5°取一个值，共计11个值，为了控制变量，滑体和滑床的其他的参数采取同样方法步骤取值，工况1和工况2岩土体各参数敏感性曲线如图7～8所示．曲线的斜率大小即为相对应的参数与稳定系数相关性的大小(相关系数)，正值为正相关，负值为负相关，且斜率的绝对值越大说明相关系数越大，相关性越强，表征该参数对滑坡的稳定系数影响也越大，各参数敏感性曲线交点所对应得稳定系数为各参数均取组中值时计算出的值，一般的等于可靠度分析中的稳定系数均值．

3.1可靠度分析

观察图5(a)可知，由蒙特卡罗随机抽样3 000次模拟计算得，工况1滑坡平均稳定系数μF为1.129，最小稳定系数Fmin为0.673，最大稳定系数Fmax为1.658，标准差σF为0.106，则代入公式(3)可得可靠性指标β为1.211，则φ(β)为0.89，将φ(β)代入式子(4)可得失效概率PF为11%，稳定系数概率分布函数即失效概率分布函数如图5(b)所示．

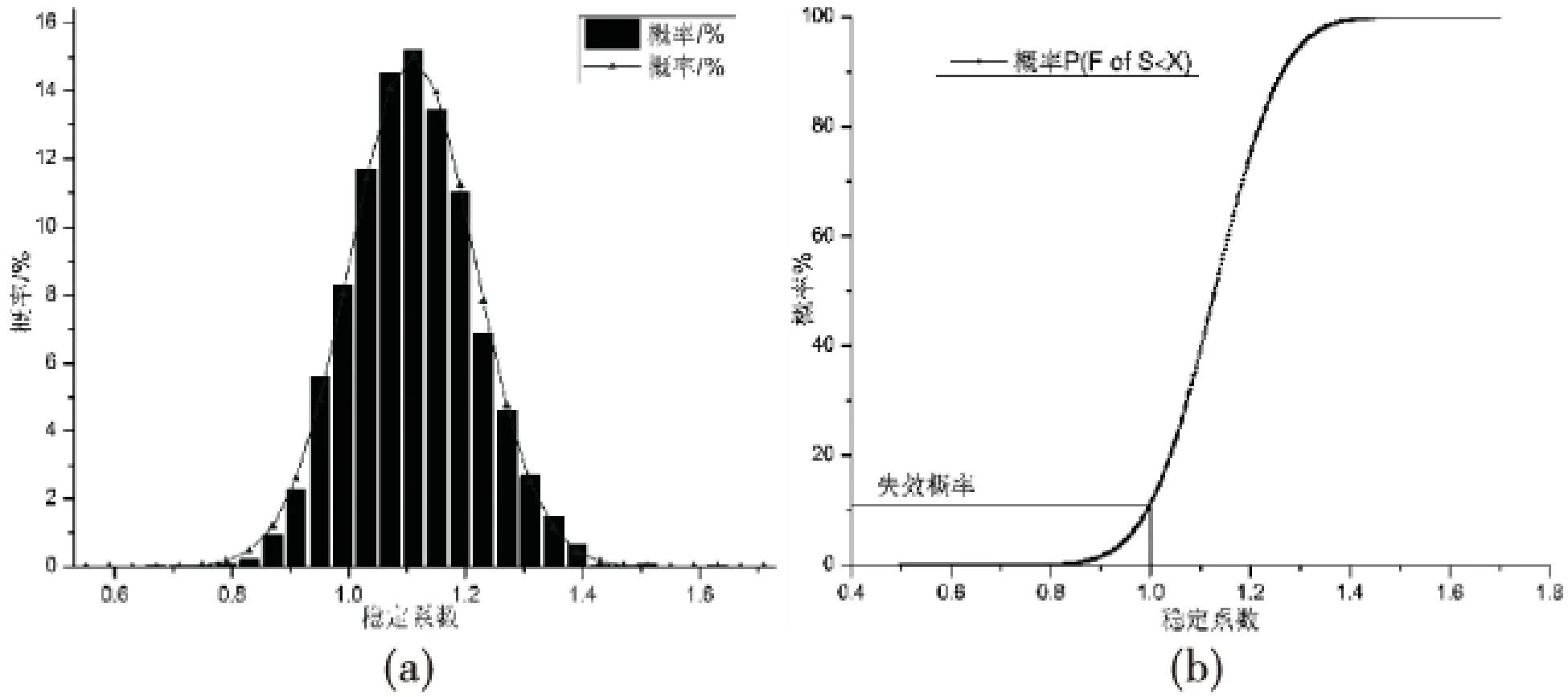
图5　工况1稳定系数概率密度函数与稳定系数概率分布函数

观察图6(a)可知，由蒙特卡罗随机抽样3 000次模拟计算得，工况2滑坡平均稳定系数μF为1.103，最小稳定系数Fmin为0.668，最大稳定系数Fmax为1.611，标准差σF为0.101，则代入公式(3)可得可靠性指标β为1.016，则φ(β)为0.85，将φ(β)代入式(4)可得失效概率PF为15%，稳定系数概率分布函数即失效概率分布函数如图6(b)所示．

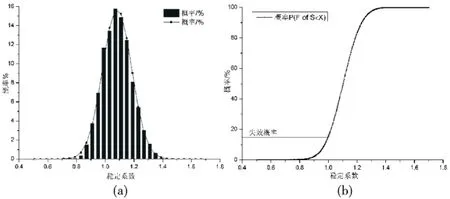
图6　工况2稳定系数概率密度函数与稳定系数概率分布函数

对比工况1和工况2可知，工况2的平均稳定系数μF和可靠性指标β均大于工况1的相应值，这和设计工况相符．分析认为：工况2考虑了库水作用及孔隙水压力作用，相较于工况1稳定性有所下降，同时工况2和工况1的最小稳定系数Fmin几乎一致，这反映了两种工况下，最不利组合是相似的，都是采取抽样岩土体最小的粘聚力c，内摩擦角Φ，最大重度γ计算出的，考虑库水及孔隙水压力后对其最不利组合稳定性影响并不大，但工况2和工况1的最大稳定系数Fmax相差较大，这说明考虑了库水重力及孔隙水压力作用对其最有利组合计算出的稳定系数影响较大．

3.2敏感性分析

观察图7可知，滑体重度γ的敏感性曲线斜率为-0.033 28，粘聚力c的敏感性曲线斜率为0.027 74，内摩擦角Φ的敏感性曲线斜率为0.259 73，而滑床岩土体参数：重度γ，粘聚力c，内摩擦角Φ的敏感性曲线斜率为0．分析认为：滑体重度γ的敏感性曲线斜率为负值，表明滑体重度与稳定系数呈现负相关关系，随着滑体重度的增加，稳定系数下降，且由其斜率绝对值可以看出，这种负相关的相关性并不明显，这是符合工程实例的．粘聚力c、内摩擦角Φ敏感性曲线的斜率为正，表明滑体粘聚力c、内摩擦角Φ与稳定系数呈现正相关关系，即随着滑体粘聚力c、内摩擦角Φ的提高，稳定系数增加，且对比粘聚力c、内摩擦角Φ敏感性曲线斜率的绝对值，内摩擦角Φ相应斜率绝对值明显大于粘聚力c相应斜率绝对值，表征滑体内摩擦角Φ与稳定系数的正相关性远大于粘聚力c与稳定系数的正相关性．而滑床岩土体各参数敏感性曲线斜率为0，表征了滑床岩土体各参数与滑坡稳定系数不相关或相关性极小，可忽略不计．观察工况1最危险画面(如图9所示)，经优化计算后的滑面全部位于滑体内部，与滑床无相交，即滑床各物理参数与稳定系数不相关．

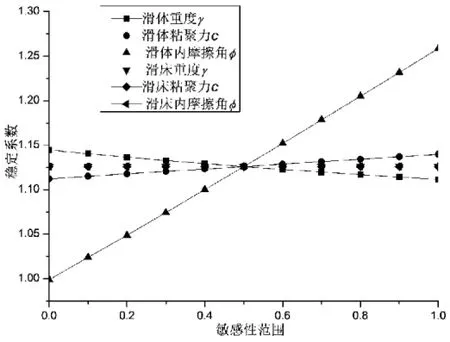
图7　工况1岩土体各参数敏感性分析曲线

同理，对比图8，可得到与工况1即图7中相似特征，值得注意的是，工况2中滑体重度γ的敏感性曲线斜率为-0.030 36，粘聚力c的敏感性曲线斜率为0.032 45，内摩擦角Φ的敏感性曲线斜率为0.247 68，滑床岩土体各参数敏感性曲线斜率为0，与工况1相比，滑体重度γ与内摩擦角Φ对应敏感性曲线斜率绝对值有所变小，粘聚力c对应敏感性曲线斜率绝对值有所增大．分析认为：工况2考虑了库水作用及孔隙水压力作用后，削弱了滑体重度γ、内摩擦角Φ对滑体稳定性的相关性，同时凸显了粘聚力c对滑坡稳定系数的影响，相关性增强．

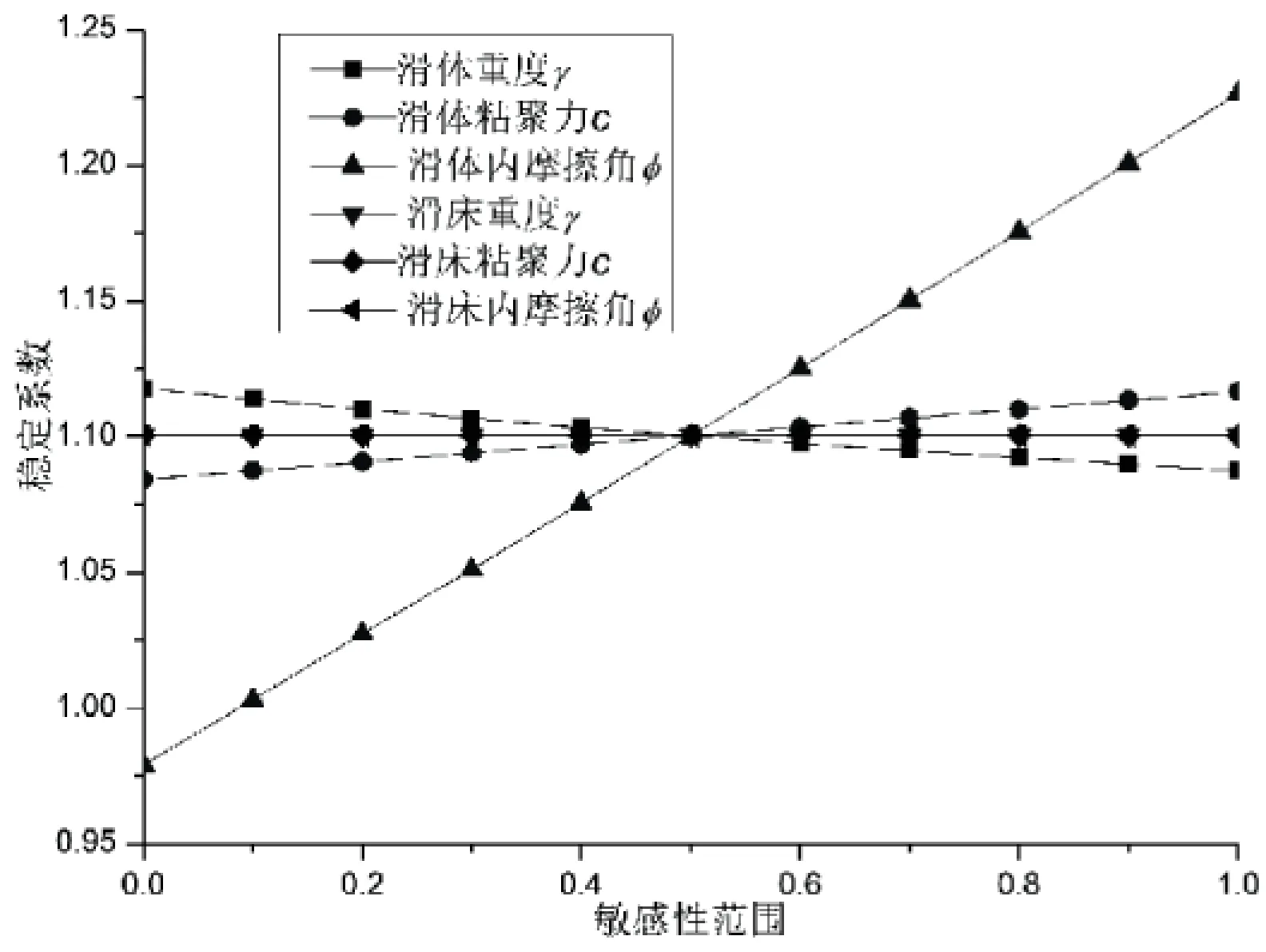
图8　工况2岩土体各参数敏感性分析曲线

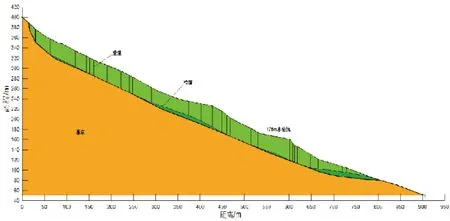
图9　工况1最危险滑动面

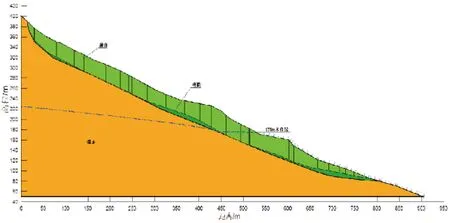
图10　工况2最危险滑动面

4结语

1)相较于传统单一确定的稳定系数法，基于可靠度理论的蒙特卡罗随机模拟算法，给出了滑坡的可靠度指标，失稳概率，最优、最不利组合的稳定系数，对滑坡稳定性评价更加客观全面．

2)考虑了库水及孔隙水压力作用后的工况2相较于工况1而言，稳定系数均值和可靠度均有所下降，工况2与工况1最不利组合的稳定系数相差不大，但工况1最优组合的稳定系数明显大于工况2，表明考虑库水及孔隙水压力作用后对其最优组合稳定系数影响较大．

3)滑坡工况1及工况2敏感性分析表明，滑体重度γ与稳定系数呈现微弱负相关，滑体粘聚力c、内摩擦角Φ与稳定系数呈正相关，且内摩擦角Φ与滑坡稳定系数的正相关性远大于粘聚力c与稳定系数的正相关性，滑床各物理力学参数与稳定系数的相关性为0，滑坡的稳定性与滑床不相关或相关性极小，观察临界滑面，符合工程实例．

4)工况2滑体重度γ与内摩擦角Φ对应敏感性曲线斜率绝对值小于工况1，粘聚力c对应敏感性曲线斜率绝对值大于工况1．表明考虑了库水作用及孔隙水压力作用后，削弱了滑体重度γ、内摩擦角Φ对滑体稳定性的相关性，同时凸显了粘聚力c对滑坡稳定系数的影响，相关性增强．

参考文献：

[1]易武，孟召平，易庆林．三峡库区滑坡预测理论与方法[M]．北京：科学出版社，2011．

[2]尹小涛，王水林．基于可靠度理论的滑坡稳定性及其影响因素分析[J]．岩土力学，2008，29(6)：1151-1156．

[3]郑颖人，赵尚毅．有限元强度折减法在土坡与岩坡中的应用[J]．岩石力学与工程学报，2004，23(19)：3381-3388．

[4]Morgenstern N R．The Influence of Groundwater on Stability，Instability in open Pit Ming (Brawner CO，.and Milligan V.eds.)[J]． Society of Mining Engineers，American Institute of Mining，Metallurgical and Petroleum Engineers，New York, 1971：65-81．

[5]陈祖熠．土质边坡稳定分析(原理·方法·程序)[M]．北京：水利水电出版社，2003．

[6]赵尚毅，时为民，郑颖人．边坡稳定性分析的有限元法[J]．地下空间，2001，21(5)：450-454．

[7]郑惠峰，汪卫明，陈胜宏．弹粘塑性块体单元法在龙滩水电站右坝肩边坡稳定分析中的应用[J]．岩土力学，2006，27(1)：107-111．

[8]夏元友，熊海丰．边坡稳定性影响因素敏感性人工神经网络分析[J]．岩石力学与工程学报，2004，123(16)：2703-2707．

[9]陈伟，许强，王朝阳．蒙特卡洛法在滑坡稳定性可靠度分析中的应用[J]．路基工程，2011(4)：135-137．

[责任编辑张莉]

收稿日期：2015-12-21

基金项目：湖北省科技支撑计划项目(2015BCE070)；水电工程智能视觉监测湖北省重点实验室开放基金 (2014KLA11)；国家自然科学基金青年基金(41302260)

通信作者：易武(1966-)，男，教授，硕士生导师，研究方向为边坡稳定性及其预测预报．E-mail：yiwu@ctgu.edu.cn

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.005

中图分类号：P642.22

文献标识码：A

文章编号：1672-948X(2016)02-0019-05

Reliability Analysis of Reservoir Bank Landslide Based on Monte Carlo Simulating Method——Taking a Landslide in Three Gorges Reservoir Area for Example

Yan Guoqiang1,2,3Yi Wu1,2,3Deng Yonghuang4Liu Qing1,2,3Huang Haifeng1,2,3

(1. College of Civil Engineering & Architecture, China Three Gorges Univ., Yichang 443002, China; 2. The Collaborative Innovation Center for Geo-Hazards & Eco-Environment in Three Gorges Area, China Three Gorges Univ., Yichang 443002, China； 3. National Field Observation & Research Station of Landslides in Three Gorges of Yangtze River, Yichang 443002, China; 4. College of Science & Technology, China Three Gorges Univ., Yichang 443002, China)

AbstractIn this paper, based on Monte Carlo random sampling algorithm, by sampling 3000 times of simulation to the Three Gorges reservoir bank landslide analysis of the stability of two kinds of working conditions, the results show that：considering the 175 m reservoir water level and pore water pressure, the average stability coefficient and reliability index is lower while the failure probability is higher in the condition 2; the stability coefficient of the most unfavorable combination shows no big differences while the optimal combination differs greatly; the gravity density of slide mass showed slight negative correlation to safety factor while the cohesive force and angle of internal friction are positively related to stability coefficient; and internal friction angle is greater than the cohesive force; there is no correlation between the slide bed parameters and stability coefficient; Compared to condition 1, the correlation between stability coefficient with the gravity density and angle of internal friction weakens and the correlation between cohesive force and stability coefficient enhances in condition 2.

KeywordsMonte Carlo simulating method;reliability analysis;Three Gorges reservoir area;landslide