近距离空间交叉盾构隧道列车振动响应特性研究
2016-08-01晏启祥徐亚军段景川
晏启祥,徐亚军,陈 诚,段景川,耿 萍
(1.西南交通大学交通隧道工程教育部重点实验室,成都 610031;2.中国电建集团成都勘测设计研究院有限公司,成都 610072;3.中水电南方建设投资有限公司,广东深圳 518000)
近距离空间交叉盾构隧道列车振动响应特性研究
晏启祥1,徐亚军1,陈诚2,段景川3,耿萍1
(1.西南交通大学交通隧道工程教育部重点实验室,成都610031;2.中国电建集团成都勘测设计研究院有限公司,成都610072;3.中水电南方建设投资有限公司,广东深圳518000)
摘要:针对目前国内近距离空间交叉盾构隧道工程,采用拟合的列车振动荷载公式,考虑列车的行驶效应,通过在轮轴对上施加振动力时程曲线,同时给予轮轴一定的行驶速度来研究列车振动作用下空间交叉盾构隧道的动力特性。在特定列车行驶速度和围岩条件下,交叉位置对应上下隧道截面的应力和加速度情况进行分析,并对上下交叉隧道纵向不同位置的加速度时程响应进行研究。获得上部和下部隧道交叉截面第一主应力和加速度分布形态及其相对不同交叉净距的变化趋势,揭示了列车在隧道内行驶时,特定观测点出现明显动力响应存在一个对应的影响区,对比下部隧道交叉处(纵向中截面)位置点的加速度响应值与其左右各点相应加速度在数值大小和一阶频率上的区别。研究所得结论对高速铁路空间交叉盾构隧道的设计具有一定的参考价值。
关键词:空间交叉隧道;列车振动效应;行驶效应;包络线;时程曲线
随着国内大中城市着力构建立体的现代化交通体系以及提速铁路和高速铁路的快速发展,出现了越来越多的空间交叉隧道。如新建渝利铁路引入重庆综合交通枢纽火风山隧道,上跨渝怀铁路新人和场隧道,交叉部位的最小距离仅5.47 m,皖赣双线铁路与九景衢铁路在景德镇市出现隧道交叉,其最小交叉距离仅为4.5 m;温福铁路琯头岭隧道下穿同温福高速公路琯头岭隧道,铁路隧道拱顶距公路隧道基底约2.91 m;新建扒挪块隧道与既有贵昆线狮子口隧道交叉,其岩层净距为13.85 m;其他如湘黔铁路增建Ⅱ线坪口隧道和流潭隧道、贵昆铁路六沾复线乌蒙山与新梅花山隧道也出现了多处空间交叉隧道工程。一般而言,空间交叉隧道根据其相对关系可划分为空间正交型交叉隧道、空间斜交型交叉隧道、空间平行型交叉隧道3类,其中,尤以空间正交型交叉隧道最为典型。
空间交叉隧道在高速列车振动荷载作用下,隧道自身和邻近隧道不可避免地会产生损伤。通常而言,列车振动不会立即引起隧道结构的破坏,但在动力荷载的长期反复作用条件下,尤其是在隧道结构工作数十年性能逐渐劣化的情形下,持续的列车振动效应可能会使隧道结构自身以及周围邻近的隧道发生较大的强度衰减,从而危及隧道和列车的运行安全。因此,研究列车振动荷载作用下隧道结构及其相邻隧道、尤其是空间交叉隧道结构的动力响应特性,对于今后分析隧道的稳定性和长期安全性具有十分重要的意义。
1列车振动研究现状
目前,国内外针对列车振动对隧道结构的动力响应已经开展了较多的研究工作。高峰、关宝树等[1]以深圳地铁某重叠隧道为例,分别针对上行、下行和上下交会动载情况下重叠隧道的动力响应进行研究;白冰和李春峰[2]对列车荷载作用下近距离平行隧道的土体-隧道结构体系进行了弹塑性动力响应分析;龚伦、郑余朝等[3]采用三维有限元对列车振动荷载作用下下穿隧道的动力响应进行模拟和研究;Sheng等[4]基于移动格林函数发展了离散波数虚拟力法,以此分析研究铁路隧道在移动谐载作用下的振动响应;李德武[5]采用现场测试的手段,分析研究了列车振动荷载对隧道衬砌结构的影响;晏启祥、陈诚等[6]采用拟合的列车振动荷载,对不同列车速度以及不同围岩情况下盾构隧道联络横通道的动力特性进行分析;丁祖德、彭立敏等人[7]针对既有铁路隧道底部结构,开展了低速列车动载作用下的隧道底部结构动力响应的数值分析;丁伯阳、宋新初等[8]根据两相饱和介质Green函数,推导了集中冲击荷载与简谐荷载圆形断面隧道内振动位移反应表达式闭合解;张曦、唐益群等[9]研究了地铁经过时引起隧道周围饱和软黏土的动力响应和超孔隙水压力;王鑫,刘增荣等[10]研究了隧道半径、壁厚、长度以及隧道埋深对隧道结构振动特性的影响;汪伟松[11]结合新梅花山隧道和乌蒙山隧道立体交叉问题,针对上跨隧道列车荷载与下穿隧道单线列车荷载等多个工况开展了动力响应分析,除此以外,高玄涛、宁茂权等[12-14]也针对列车振动作用下地层与隧道衬砌的动力响应做了相应的研究。
上述研究大多集中在单条隧道或平行隧道的动力瞬态响应问题上,且主要依托列车荷载-平面隧道结构-围岩二维模型开展固定位置振动荷载的研究,对于空间正交隧道,建立列车荷载-隧道结构-围岩三维模型,考虑列车荷载的行驶效应对结构自身和邻近隧道的振动响应的影响研究尚不多见。
2空间交叉隧道模型
列车振动分析采用隐式H.H.T法时间积分法[15]求解,振动系统阻尼采用Rayleigh阻尼,阻尼比ζ0取为0.05,动力计算边界条件采用三维一致黏弹性人工边界,其切向与法向黏弹性人工边界修正系数分别取为0.67和1.33。列车振动荷载采用国际通行的时程拟合公式生成,对于列车轴重为170 kN,簧下质量为M0=750 kg,时速350 km/h的列车振动问题,其荷载时程拟合曲线见图1。

图1 350 km/h速度下车轮轴振动荷载曲线

图2 空间交叉结构数值模型
由于目前国内尚未有超近距离两两正交高速铁路隧道的工程实例,为分析方便,数值模型选用虚拟的相同结构和截面的正交盾构隧道组成,两正交盾构隧道外径都为10.8 m,内径都为9.8 m,不考虑管片之间的接头效应,上部隧道埋深保持35 m不变,下部隧道与上部隧道的垂直净距分别取为2.0、3.0、4.0 m,隧道空间交叉模型如图2所示。围岩选用向蒲铁路戴云山隧道上统长林组(J3C)Ⅲ级粉砂岩。数值模型尺寸为长500.0 m×宽160.0 m×高80.0 m,地层假定为均一地层,上边界为地面,其余边界均为一致黏弹性人工边界。
考虑列车编组为8节车厢,单长度为25.0 m,每节车辆的前后各有两对靠近的轮轴,共计32对轮轴。衬砌、轨道、围岩均采用实体单元模拟,弹塑性本构关系,屈服准则选用摩尔库伦准则。衬砌、轨道、岩土体的物理力学参数见表1。

表1 物理力学参数
在列车行驶的上部隧道(以下简称A隧道)中建立轨道模型,模拟列车在A隧道中行驶对自身和下部隧道(以下简称B隧道)的影响。列车开始实施振动的初始位置为车头,位于入口内200 m处。考虑列车的行驶效应,在列车初始轮轴对上施加随时间变化的振动荷载,并同时随列车向前行驶持续改变荷载的作用位置,模拟列车行进距离300 m。从轨道所受荷载来看,这种大小在时间上变化,作用点在空间上变化的荷载施加方式相对过去的在特定区段固定位置上施加随时间变化振动荷载的方式,能更加有效地模拟列车的真实运动情况、揭示列车振动的行驶效应,列车振动荷载施加示意如图3所示。
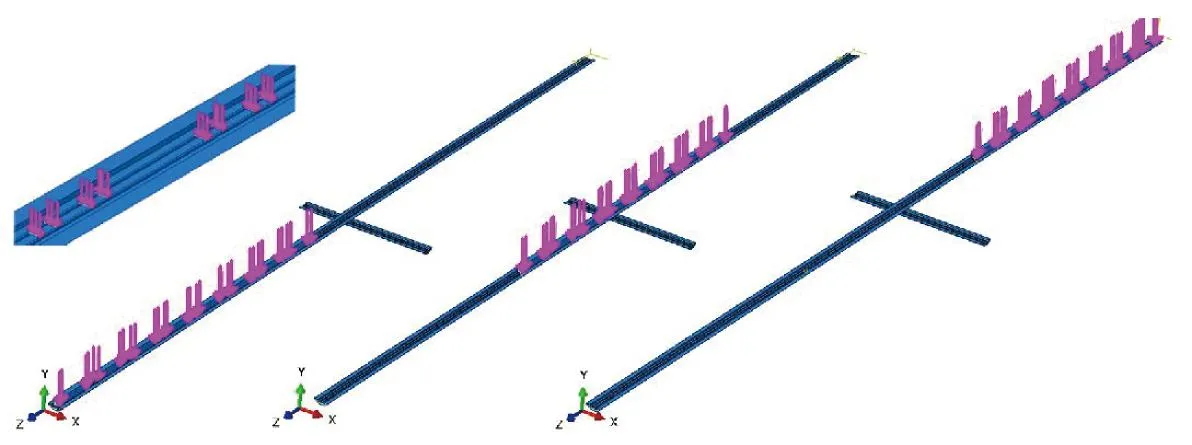
图3 列车振动荷载施加示意
3衬砌结构振动响应特性
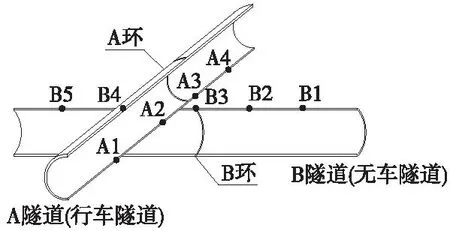
图4 位置点和典型截面示意
为便于分析,首先需要在交叉隧道上选取典型截面和数值提取点。将B隧道纵向中剖面与正交A隧道相交所形成的截面称为A截面,将A隧道纵向中剖面与正交B隧道相交所形成的截面称为B截面,如图4所示。并在A隧道拱底沿列车行进方向设置了A1、A2、A3、A4四个数值提取点,A1、A2、A3、A4离A隧道入口的距离分别为72、144、288、360 m,在B隧道拱顶设置了B1、B2、B3、B4、B5五个数值提取点,B1、B2、B3、B4、B5离B隧道右侧入口分别为16、48、80、112、144 m。围岩级别为Ⅲ级,列车行驶速度为350 km/h。
3.1不同净距下列车振动对A隧道的影响
列车振动传播效应不仅与结构自身有关,也与周边隧道围岩和邻近隧道结构的分布位置有关,对于围岩和隧道结构型式确定的地下空间交叉结构,分布位置中一个最显著因素就是两相邻隧道的净距。图5为A隧道所属A截面在不同净距时的时程范围内第一主应力包络线。可以看出,管片第一主应力包络线大致沿竖向对称分布,第一主应力最大值出现在左右下方45°位置附近,最小值出现在拱顶,拱底处会出现一个相对最大值较小的极大值;2.0、3.0 m和4.0 m三种不同净距对应的第一主应力最大值分别为26 191.0,22 035.0、11 336.1 Pa,对应的最小值分别为624.0、561.0和198.3 Pa,表明A截面第一主应力最大值和最小值均随着交叉隧道净距的增加而减小。

图5 A截面在不同净距时σ1最大值包络线(单位:Pa)
图6为3种净距下A截面时程范围内加速度包络线。加速度包络线大致沿竖向对称,在隧道底部中央加速度最大;2.0、3.0和4.0 m 3种不同净距对应的加速度最大值分别为7.173、4.766和2.573 cm/s2,加速度最小值分别为0.175、0.181、0.223 cm/s2,表明A截面加速度最大值随着净距的增大而减小,且在一定净距范围内,最小值随着净距的增大而增大。
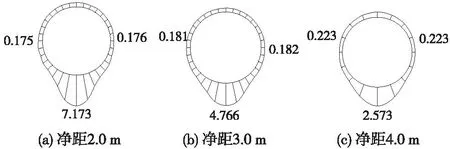
图6 A截面不同净距加速度最大值包络线(单位:cm/s2)
3.2不同净距下列车振动对B隧道的影响
图7为列车在A隧道行驶时,振动引起的B隧道所属B截面在3种垂直净距下的第一主应力时程范围包络线。可以看出,第一主应力最大值均出现在顶拱上,最小值均出现在左右拱腰部位,第一主应力从拱顶到拱底呈现先减小再增大的趋势;2.0、3.0和4.0 m三种不同净距下,第一主应力最大值分别为5 665.0、4 424.0 Pa和3 548.0 Pa,第一主应力最小值分别为150.0、194.0 Pa和324.0 Pa,表明第一主应力最大值随着净距的增大而减少,且在一定净距范围内,最小主应力随着净距的增大而增大。

图7 B截面在不同净距时σ1最大值包络线(单位:Pa)
图8为B截面加速度包络线。图中可以看出,B截面加速度最大值均出现在隧道顶拱上,最小值均出现在隧道底拱上,加速度的值以拱顶为中心,向两侧大致呈均匀减少并至拱底达最小值的趋势。且加速度最大值随着净距的增大而减小,在一定净距范围内,加速度最小值随着净距的增大而增大。
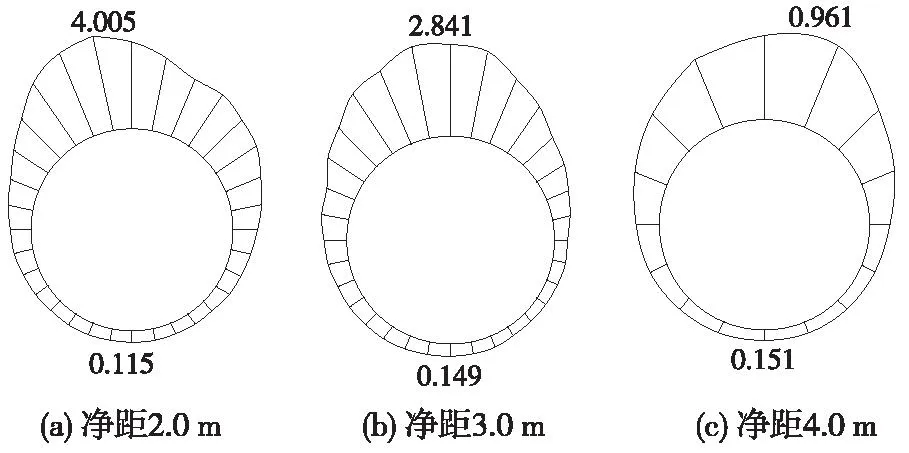
图8 B截面不同净距加速度最大值包络线(单位:cm/s2)
3.3A隧道不同位置加速度时程特性
前述分析可知,当列车在空间正交相邻结构上部隧道行驶时,上部隧道的加速度最大值通常出现在隧道底拱中央,下部隧道加速度最大值通常出现在隧道顶拱附近,为此,选取3.0 m净距的两隧道,分析350 km/h速度下,上部A隧道底拱中央纵向A1、A2、A3、A4四个数值提取点的加速度时程曲线,分别见图9~图12。
图9可以看出,由于A1点位于列车开始行驶振动位置中编组的后半段,大致在第6节车辆的前端,因此其加速度很快达到5.0 cm/s2的较大水平,并在0.72 s后,即列车车尾通过A1点后加速度开始快速下降并逐渐消失。图10表明,当列车尾部通过A2点,即1.44 s时,加速度才开始明显下降;在整个[0 s,1.44 s]之间,列车的第三节至最后第八节依次通过A2点,其加速度最大值始终在5.0 cm/s2附近波动。
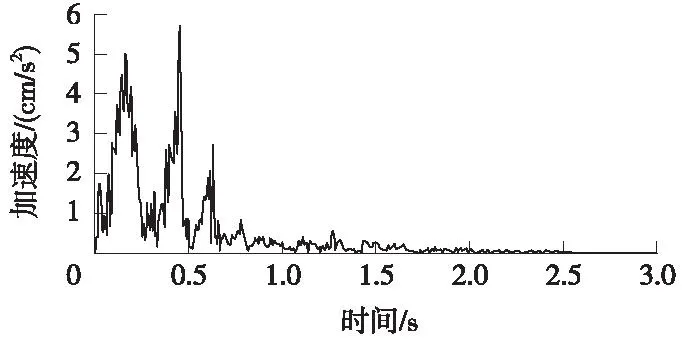
图9 A1点加速度时程曲线
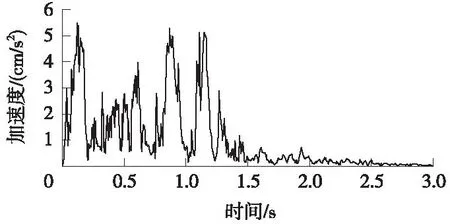
图10 A2点加速度时程曲线
图11表明,随着列车向A3点驶来,在0.42 s时刻加速度开始逐渐上升,当列车车头通过A3点时,即0.88 s时,A3的加速度突然呈现明显上升,在列车通过A3点[0.88 s,2.88 s]整个时段内,第2节和第6节车辆通过时加速度响应最大。图12中列车到达A4点的时间为1.60 s,到达前1.20 s即0.4 s时加速度响应已然非常明显。

图11 A3点加速度时程曲线
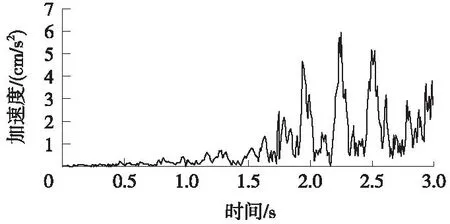
图12 A4点加速度时程曲线
上述加速度时程曲线表明,列车车头通过直至车尾通过特定点的整个过程,加速度响应最为明显,且隧道纵向各位置点的加速度最大值较为接近;与此同时,就本算例而言,列车车头到达观测点前120 m和车尾驶离观测点后80 m,也有明显的加速度响应存在;A1、A2、A4相对更加邻近下部隧道的A3点而言,加速度频谱只出现轻微变化。
3.4B隧道沿长度方向不同位置加速度时程特性
图13~图17为下部B隧道拱顶5个数值提取点的加速度时程变化曲线。每条加速度曲线变化形态均相似,时程曲线中部幅值较高、加速度波动较大,列车接近交叉位置前和驶离交叉位置后加速度较低,表现为时程曲线两侧幅值较低,加速度波动较小。交叉位置对应点B3的加速度最大值达2.05 cm/s2,其他B1、B2、B4、B5各点的加速度最大值在0.37~0.40 cm/s2,表明距离交叉位置对应点B3一定距离各点的加速度下降非常明显。从振动频率来看,处于交叉位置的B3点,其振动基本以低阶振动频率为主导,振动周期非常明显,一阶频率相对其他各数值提取点的一阶频率低,且离交叉点越远,其一阶振动频率越大。
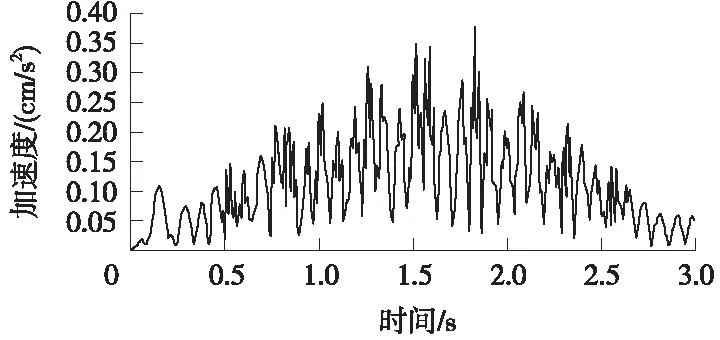
图13 B1点加速度时程曲线
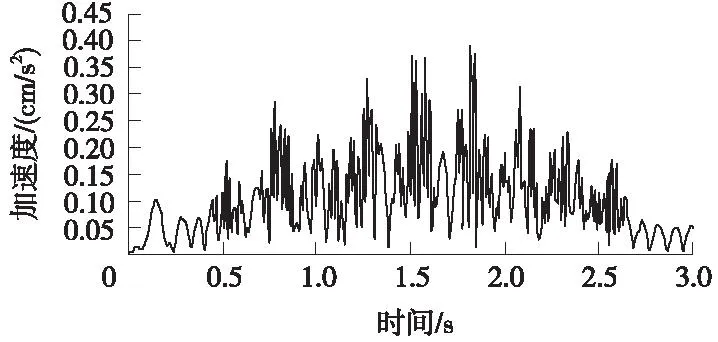
图14 B2点加速度时程曲线
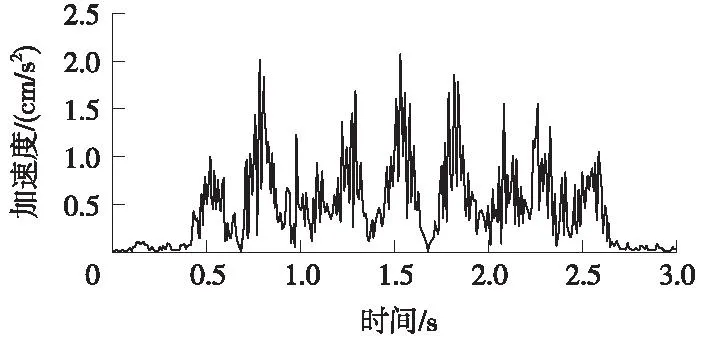
图15 B3点加速度时程曲线
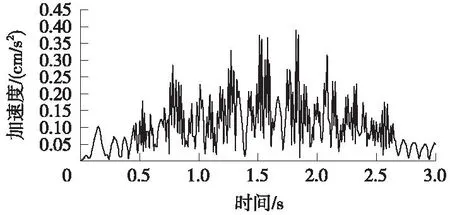
图16 B4点加速度时程曲线
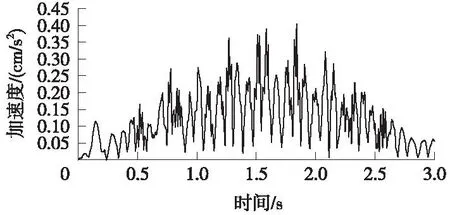
图17 B5点加速度时程曲线
4结论
利用列车振动荷载拟合公式,采用H.H.T法时间积分法对某算例进行了两两空间正交隧道动力特性分析,模拟了列车在上部隧道高速行驶对隧道自身和下部隧道的影响,得到以下结论。
(1)通过在轮轴对上施加振动力时程曲线,并在列车车轮上施加列车前进方向的行驶速度场,可以模拟振动荷载的大小和位置变化,从而可以较为精确地模拟列车振动荷载的行驶效应,揭示隧道结构动力响应随列车行驶速度和位置的发展变化。
(2)空间正交隧道中,列车振动荷载将引起上部隧道左右侧下方45°附近部位和下部隧道顶拱部位第一主应力响应最大,而上部隧道拱顶和下部隧道左右拱腰部位第一主应力响应最小;列车振动荷载将引起上部隧道底部中央和下部隧道顶部附近加速度响应最大,上部隧道顶部和下部隧道底部加速度响应最小。
(3)空间正交隧道交叉位置对应上部和下部隧道第一主应力和加速度的动力响应最大值随着净距的增大而减小,而其第一主应力和加速度动力响应的最小值在一定净距范围内可能出现随净距增大而增大或随净距增大而减小两种情况。
(4)无论是上部隧道还是下部隧道上的特定点,当列车整个编组通过该点的整个过程当中,其加速度响应最大,就本算例而言,列车车头到达观测点前和车尾驶离观测点后一定距离范围,加速度响应依然较为明显,说明列车振动相对某一特点观测点,存在一个列车行驶振动的影响区。
(5)下部隧道交叉点位置的加速度响应明显大于其左右各点的加速度响应。由于上部隧道的存在,下部隧道交叉点振动响应的一阶频率相对其左右各点的一阶频率低,且离交叉点越远,其一阶振动频率越大。
上述结论是在某一算例的条件下获得的,具有一定的局限性,今后应在实体工程的基础上开展深入的分析工作,包络研究不同隧道长度、不同列车编组和列车行驶速度、不同围岩条件和净距、不同隧道断面面积和型式等因素对交叉隧道振动响应的影响分析工作。
参考文献:
[1]高峰,关宝树,仇文革,等.列车荷载作用下地铁重叠隧道的响应分析[J].西南交通大学学报,2003,38(1):38-42.
[2]白冰,李春峰.地铁列车振动作用下近距离水平隧道的弹塑性动力响应[J].岩土力学,2009,30(1):123-128.
[3]龚伦,郑余朝,仇文革.列车动载引起下穿隧道振动三维数值分析[J].现代隧道技术,2008,45(4):23-27,43.
[4]SHENG. X,JONES. C J C,THOMPSON.D J.A theoretical model for ground vibration from trains generated by verttical track irregularities[J].Sound and Vibration,2004,272(3-5):937-965.
[5]李德武.列车振动对隧道衬砌影响的分析[J].兰州铁道学院学报,1997,16(4):24-27.
[6]晏启祥,陈诚,黄希,等.盾构隧道与横通道交叉结构的列车振动响应特性分析[J].土木工程学报,2015,48(S1):228-235.
[7]丁祖德,彭立敏,雷明峰,等.高速铁路隧道列车振动响应影响因素分析[J].铁道科学与工程学报,2011,8(4):1-6.
[8]丁伯阳,宋新初,袁金华.饱和土隧道内集中荷载作用下振动位移反应的Green函数解答[J].工程力学,2009,26(6):153-157.
[9]张曦,唐益群,周念清,等.地铁振动荷载作用下隧道周围饱和软黏土动力响应研究[J].土木工程学报,2007,40(2):85-88.
[10]王鑫,刘增荣,李云璋.基于土与结构相互作用的隧道结构振动特性的理论研究[J].地震工程与工程振动,2010,30(5):142-149.
[11]汪伟松.列车荷载作用下立体交叉隧道结构动力响应分析[D].成都:西南交通大学,2009.
[12]高玄涛.高速铁路列车振动荷载对下穿隧道地层动力响应分析[J].铁道标准设计,2014,58(6):93-97.
[13]宁茂权.列车荷载作用下深厚饱和软土盾构隧道沉降分析[J]. 铁道标准设计,2015,59(10):94-98.
[14]李宇杰,王梦恕,宋国侠,等.地铁列车振动对既有矿山法隧道衬砌裂缝的影响研究[J].土木工程学报,2015,48(S1):346-350.
[15]黄胜,陈卫忠,杨建平,等.地下工程地震动力响应及抗震研究[J].岩石力学与工程学报,2009,28(3):483-490.
收稿日期:2015-10-18; 修回日期:2015-11-24
基金项目:国家自然科学基金资助项目(51278425,U1134208,51178400)
作者简介:晏启祥(1971—),男,教授,博士,E-mail:764365015@qq.com。
文章编号:1004-2954(2016)06-0060-05
中图分类号:U451+.3
文献标识码:A
DOI:10.13238/j.issn.1004-2954.2016.06.013
The Characteristic Analysis of Short Distance Space Geometry Shield Tunnel under Train Vibration
YAN Qi-xiang1,XU Ya-jun1,CHEN Cheng2,DUAN Jing-chuan3,GENG Ping1
(1.Key Laboratory of Transportation Tunnel Engineering,Ministry of Education,Southwest Jiaotong University, Chengdu 610031,China; 2.Powerchina Chengdu Engineering Corporation Limited,Chengdu 610072,China; 3.Sinohydro South Construction Investment Co.,Ltd.,Shenzhen 518000,China)
Abstract:This paper aims at solving the current problem of short distance space geometry shield tunnel engineering in China by using the fitting train vibration load formula and applying vibration force time history curves and velocity to the wheel axles to simulate the effect of running train and analyze the dynamic characteristics of space geometry structures. This paper analyzes major principal stress and acceleration envelope curve of the cross position at a specific train speed and level of surrounding rock,and studies the response of acceleration time history at different locations of the upper and lower parts of the tunnel. The present study focuses on the distribution of the first main stress and acceleration and the trend of changes in different distances. The results conclude that when a train running in the tunnel,there is a train influencing area corresponding to the dynamic response of observation points,and difference exists between the intersection of lower tunnel and other observation points in acceleration response value and first frequency. The conclusion may serve as a reference for the space geometry shield tunnel construction of high-speed railway.
Key words:Space geometry tunnel; Effects of train vibration; Effects of traveling; Envelope curves; Time-history curves
