基于攻击增益的工业控制系统物理层安全风险评估
2016-08-01冯冬芹
梁 耀,冯冬芹
(浙江大学 智能系统与控制研究所 工业控制技术国家重点实验室,浙江 杭州 310027)
基于攻击增益的工业控制系统物理层安全风险评估
梁耀,冯冬芹
(浙江大学 智能系统与控制研究所 工业控制技术国家重点实验室,浙江 杭州 310027)
摘要:通过借鉴多输入多输出(MIMO)系统中变量配对的思想,基于相对增益阵列(RGA)设计衡量闭环状态下每个输出对不同攻击输入的敏感程度的指标,即闭环攻击增益矩阵.结合逼近理想解(TOPSIS)法,提出定量分析工业控制系统物理层安全风险的评估方法.通过精馏塔实验平台的案例分析,直观地展现攻击效果,验证闭环攻击增益矩阵的正确性,得出控制回流比的设备区域在该控制系统物理层中安全风险最大.实验结果表明,该评估方法能较全面地结合被控对象的客观属性,科学合理地量化评估工业控制系统物理层中潜在的安全风险.
关键词:安全风险评估;工业控制系统物理层;多输入多输出(MIMO)系统;相对增益阵列(RGA);闭环攻击增益矩阵;逼近理想解(TOPSIS)
工业控制系统(industrial control system,ICS)指的是由工业被控对象和控制单元所构成的有机整体,ICS在很多领域得到了应用,包括电力、水设施、石油和天然气、化工、交通、造纸和离散制造等[1].然而,随着通用的通信网络和多样化的信息技术(information technology,IT)组件在ICS中得到了应用,使得这些领域的ICS更容易受到安全威胁[2].如何对工业控制系统进行安全风险评估成了ICS安全性研究的热点,也是本文的研究重点.
工业控制系统安全问题不仅与信息层有关,也与物理层有关[3].传统的IT系统因为很少与物理系统相关联,所以即使出现了系统安全事故,也不会影响物理环境.但在工业领域则不同,不仅信息层与物理层结合,而且因为物理层中的工业对象或过程的特点,其本身就可能存在严重的安全威胁,比如高温、高压、腐蚀、强电等.那么,信息层中的某些漏洞可能被恶意操控,使物理层中的不安全因素超出人们的可控范围,因而一旦出现安全问题,不仅会造成信息资源的损失,还会造成物理环境的破坏,甚至产生巨大的经济、环境、生命财产的损失.
关于利用信息层中的漏洞来破坏工业控制系统的安全事件已经被诸多新闻媒体所报道[4-9].作为第一个被发现的网络攻击武器,“震网”病毒[10-12]直观地展现了信息层漏洞对ICS物理层造成的严重威胁,利用“零日漏洞”有效地避免反病毒软件的检测,为破坏铀浓缩工厂中的离心机保护系统提供了保障[13].由于这些保护系统中的控制器操控了每个离心机上的阀门和压力传感器,即控制了物理层设备,使得“震网”病毒可以通过感染这些控制器来达到破坏目的.换言之,“震网”病毒找到了物理层中的脆弱点.
工控系统安全性相关研究已经认识到物理层的重要性,并且开始结合具体的被控对象模型进行研究.Mo等[14]利用线性时不变模型作为被控对象,创新性地分析了重放攻击下的攻击模型,论证了重放攻击实现的条件,并给出了检测重放攻击的措施.Cárdenas等[15]对实际的Tennessee-Eastman PCS化工过程进行数学建模,设计了可行的攻击方式,并通过仿真说明了攻击破坏反应炉中压力的有效性.Kwon等[16]从系统的角度分别分析了攻击传感器和执行器对系统造成的影响,并就无人机的导航系统进行建模仿真,重现了攻击者劫持无人机的场景.Teixeira等[17]基于网络控制的四阶水箱系统进行仿真验证,给出了攻击的场景、影响和应对措施.但是,上述研究在考虑攻击行为时,只是随机地选取某个输入量或反馈量,然后分析攻击这些量对系统性能造成的影响,并没有给出攻击选取的依据和规则,也就是说并没有真正分析物理层中对象的安全风险究竟在何处.
传统的信息安全风险评估已经取得了一定的成果[18-20],但是,由于IT系统与工业控制系统存在巨大的差异性,使得信息安全风险评估的结论不能直接应用在工业控制系统中[21].由于应用场合的不同,上述研究不能结合实际的物理层对象,所得出的指标就不能全面地反映工业控制系统的安全风险.
针对上述可以改进的地方,本文从物理层对象出发,给出工业控制系统物理层的安全风险评估办法.通过数学建模,将安全风险评估问题转化为攻击增益计算问题,并提出攻击效果的量化指标——闭环攻击增益矩阵.将每个攻击输入对所有输出产生的攻击增益进行权衡,把风险评估问题进一步转化为多属性决策问题,采用逼近理想解(technique for order preference by similarity to ideal solution, TOPSIS)法,定量给出工业控制系统安全风险的综合评估值.基于精馏塔模型进行仿真,验证前述闭环攻击增益矩阵的正确性,并找出该控制系统中安全风险最大的区域.
1问题描述
在对系统进行安全风险评估时,比较常用的是攻防对抗模型,因为攻防双方都期望找到系统中安全风险最大的地方.另外,风险评估还可以从系统自身可靠性的角度出发,通过分析系统中一个或多个组件发生故障后对系统安全的影响,进而找到风险最大的地方.虽然攻击和故障存在本质上的区别,检测方法也不同,但是对于系统的安全风险评估问题,考虑的是两者的效果,本文选择进行统一分析.这样就可以将安全风险评估问题转化成攻击效果评估问题,而评价攻击效果的一个很重要的因素就是攻击的稳态增益,因此有必要对存在攻击的控制系统进行建模分析.
1.1MIMO控制系统模型
大型工业生产过程或被控对象都是多输入多输出的(multiple input and multiple output, MIMO),因此对工业控制系统的物理层对象进行安全风险分析时,以MIMO模型作为研究对象符合客观规律.如图1所示为MIMO控制系统简化后的结构图,包括控制器、控制网络、执行器、被控对象、传感器,图中省略了执行器和传感器.假设图1中的n输入n输出对象的数学模型可以用开环传递函数表示,在任意时刻k,对象的传递函数模型如下:
Yk(s)=Gk(s)·Uk(s),
(1)

(2)
式中:Yk(s)=L[y(k)],Uk(s)=L[u(k)],y(k)=[y1(k),y2(k),…,yn(k)]T.u(k)=[u1(k),u2(k),…,un(k)]T;u(k)∈Rn是k时刻的作用在对象上的n维输入向量,uj(k)表示u(k)的第j个元素,即第j个输入;y(k)∈Rn是k时刻对象的n维输出向量,yi(k)表示y(k)的第i个元素,即第i个输出,i,j=1,2,…,n.L是拉氏变换运算符,Gk(s)是k时刻对象的开环传递函数,并假设Gk(s)是非奇异的,即输出量之间不相关.第i个回路使用的控制器为Ci.
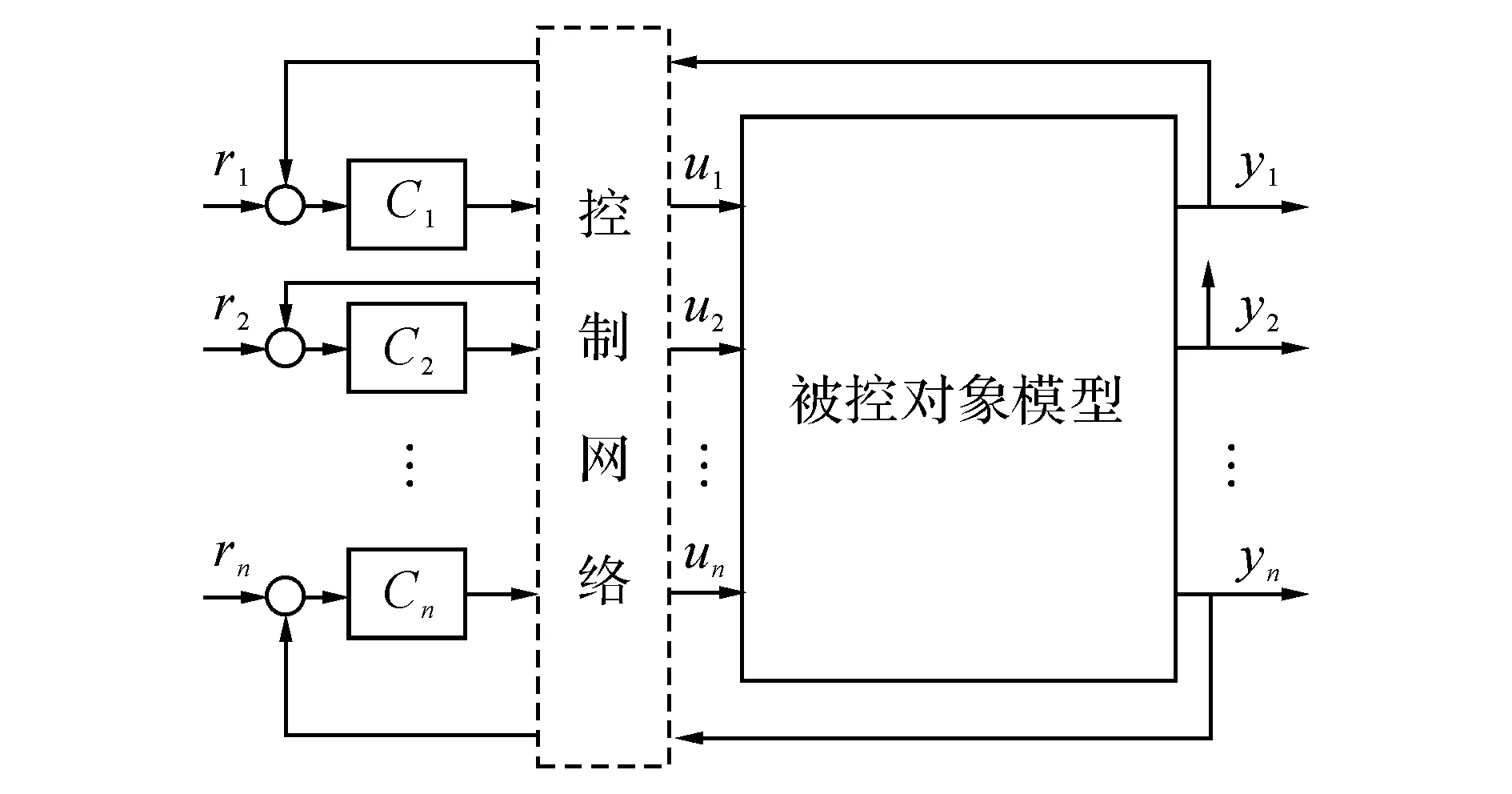
图1 多输入多输出控制系统示意图Fig.1 Schematic diagram of multiple input multiple output control (MIMO) control system
1.2攻击模型
为了找到系统中安全风险最大的区域,从攻击行为对系统的影响效果出发,假设攻击方具备下述的特点:
1) 攻击方了解控制系统的控制结构,即各回路的组成关系;
2) 攻击方了解被控对象的模型Gk(s),并且能从控制网络中获得对象任意时刻的输入、输出状态uj(k)和yi(k);
3) 攻击方能任意修改在控制网络中的数据,但攻击方仍然选择直接攻击输入向量u,因为直接攻击传感器的测量值向量y可能会造成异常检测器动作,而且攻击y最终也会通过控制器来改变作用在对象上的输入u;
4) 攻击方可以记录每个输出量的历史数据{yi(0),yi(1),…,yi(k)},并可以对任意输出量进行重放.
这样,在攻击存在的情况下,式(1)所描述的被控对象变为
(3)
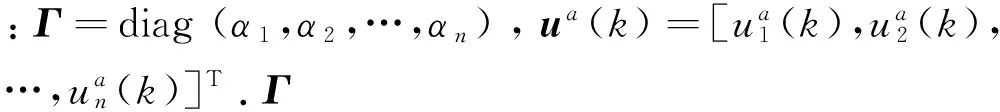
1.3主要问题
对攻击方而言,实施攻击步骤须进行3步:根据攻击目的确定关键输出量、选取攻击矩阵Γ、构造攻击数据ua(k).最理想的攻击方案选择一个最优攻击矩阵Γ,即选择一个最优攻击点,使单位攻击数据ua(k)对关键输出产生的增益最大.防御方也需要考察哪些输入对关键输出的影响程度较大,从而判断系统中可能存在的安全风险.这样就将安全风险评估问题转化为攻击增益计算问题.
但是,工业生产中的MIMO对象普遍存在耦合现象,并且MIMO对象大多处于闭环状态,这使得攻击增益的确定变得复杂,因而难以判断物理层对象中存在的安全风险.如何建立一种规则来计算攻击增益,并依此建立一种安全风险评估准则就是本文要解决的问题.
2闭环攻击增益矩阵
在MIMO控制领域,衡量输入输出耦合程度最有效的度量方法是Bristol提出的相对增益阵列(relativegainarray,RGA),而且RGA已经成功应用在实际工业过程中,如化工精馏过程、厂级能量循环等.本文借鉴RGA中输入输出关联的思想,并将这种方法应用在工业控制系统物理层对象安全风险分析中.
2.1相对增益阵列
定义1对于如图1所示的n输入n输出的对象,第j个输入uj对第i个输出yi的关联程度即相对增益(relativegain,RG)定义为除uj外其他输入量不变时输出yi对输入uj的增益与除yi外其他输出量不变时输出yi对输入uj的增益的比值,相对增益的表达式为


(4)
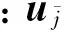
根据式(4)的定义,可以求出每个输入对每个输出的关联程度,一共n2个相对增益值,然后按照下标排列成矩阵,即构成对象的RGA:

根据Bristol[22]的研究,有
定理1RGA可以直接由开环稳态增益矩阵K求出:
(5)
式中:uss和yss分别是稳态输入和稳态输出,“.×”代表矩阵点乘,“-T”代表矩阵转置求逆;对于线性时不变系统:
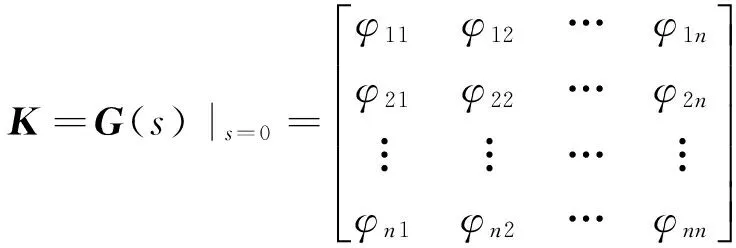
对定理1的证明如下.
令H=K-1,L=HT,则

(6)
显然,
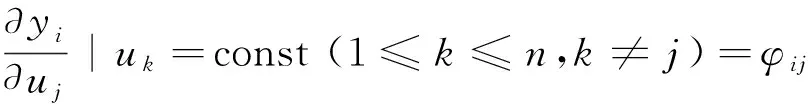
因此,如果要证明Λ=K.×K-T,只须证明式(7):
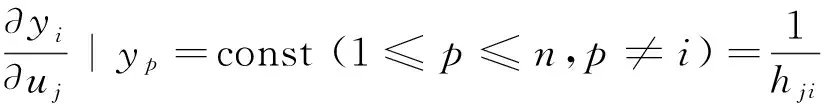
(7)
由于开环传递函数可逆,
y=K·u ⟹ u=K-1·y=H·y .
展开第j行,得
uj=hj1·y1+…+hji·yi+…+hjn·yn.
进一步转化为

(8)
即式(7)得证:
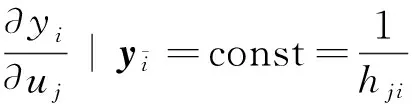
(9)
定理1得证.
2.2攻击效果量化指标
尽管RGA在分析变量关联程度上的最大优点是计算简单有效,但是,直接使用RG指标去分析物理层对象的安全风险存在2个问题:一是RGA只能定性分析MIMO对象变量的开环耦合程度,而实际的MIMO对象已经处于闭环控制结构;二是RGA只衡量了单个输出对单个输入在开环与闭环下增益的比值,而不是“相对”其他输入的增益,其结果不能描述某个关键输出对不同攻击输入对的敏感程度.因此,本节结合实际MIMO对象闭环的特点,不使用λij作为评估指标,而使用λij的分母,即输入对输出的闭环增益,作为量化值,并提出闭环状态下衡量关键输出yi对不同攻击输入敏感程度的量化指标——闭环攻击增益矩阵P,然后根据矩阵P进一步推导出MIMO系统的安全风险评估准则或攻击矩阵的选取规则.
定义2闭环攻击增益矩阵P为
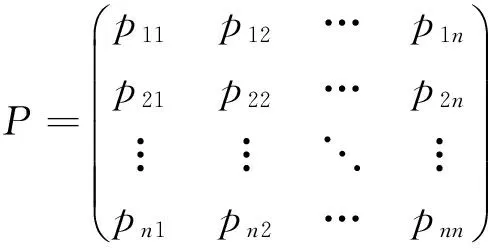
(10)
式中:
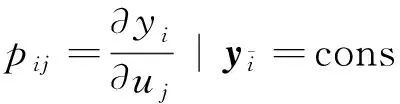
(11)
闭环攻击增益矩阵P的第i行表示在闭环条件下,选取不同的攻击输入分别对输出yi的稳态增益.选择该指标的原因有:一方面,RGA中的元素λij可以由稳态增益阵K直接求出,而且
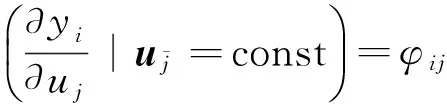
φij为矩阵K中第i行、第j列的元素,因此该指标计算简单有效;另一方面,该指标很好地满足了实际MIMO对象的闭环特征,因而能够量化闭环下不同的攻击输入对关键输出的影响程度.结果表明,矩阵P的计算同样只需要利用稳态开环增益矩阵,而不需要了解系统的精确模型,简单有效.

定理2在2种攻击情况下,攻击所产生的闭环增益为
(12)


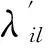
定理2的证明如下.


(13)
根据RGA的定义,
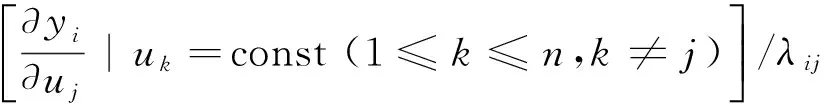
可得

(14)


(15)
根据开环传递函数可得

(16)
除去矩阵K中的第m行、第j列后,可以得到n-1个线性方程组.类似于式(8),通过求解上述线性方程组,可以将yi表达成式(17)的形式:
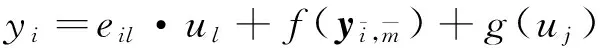
(17)
由于攻击是以增量的形式叠加在原运行点上的,可以写出式(17)形式的增量式:
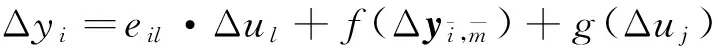
(18)
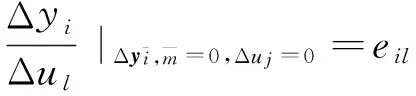
(19)
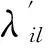
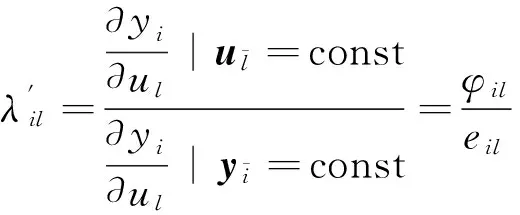
则
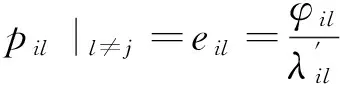
(20)

中对应下标的值.
定理2得证.
对闭环攻击增益矩阵的推导借鉴了RGA分析MIMO对象输入输出关联程度的思想.实际上,RGA的实质就是最大限度地利用开环信息对闭环性能进行预测.因此,即使闭环回路的控制器种类发生变化,抑或是控制结构发生变化,闭环攻击增益矩阵的算法仍然能保持正确性.
尽管推导来自攻击假设,但是从攻击和故障的效果分析,闭环攻击增益矩阵也可以用于分析系统可靠性问题.
3控制系统物理层安全风险评估
虽然闭环攻击增益矩阵P可以对攻击效果进行精确的衡量,但是矩阵P的元素只能反映某个攻击输入对一个目标输出的攻击增益.当控制系统存在多个输出与物理安全相关,就不能只考虑攻击对单个输出的增益,因此,有必要对攻击增益进行权衡,并给出一个综合的攻击增益评估值,然后利用这个综合评估值来衡量控制系统中物理层的安全风险.
3.1评估方法
安全风险评估问题又进一步转化成多属性决策问题,解决多属性决策问题的方法有很多,包括简单加权法、层次分析法、TOPSIS方法[23]等.其中,TOPSIS方法在多属性决策领域得到了广泛的研究和应用,其最大的优点在于计算简单,并能在统一的标准下定量给出决策集元素的评估值,因此本文选择TOPSIS方法作为安全风险评估的核心方法.
此时,输出集合Θ={y1,y2,…,yn}相当于属性集;输入集合Φ={u1,u2,…,un}相当于决策评价对象集.属性集与对象集之间的对应关系正好是闭环攻击增益矩阵P=(pij)n×n.
安全风险评估的步骤如下.
1) 属性归一化,得到标准决策矩阵
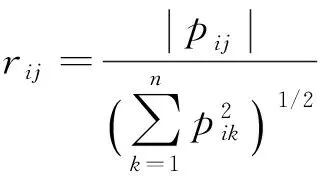
从攻击效果的角度看,安全风险评估应考虑增益的绝对值,因此标准决策矩阵Ω中的元素都取正值.
(2) 构造加权归一化矩阵T=(tij)n×n,并假设已经对每个输出的关键程度进行了评估,权重向量为
W=[ω1,ω2,…,ωn],
3) 求出正负理想解.攻击输入uj对输出yi的闭环增益绝对值越大,表征这个输入的安全风险越高,属于效益型指标:
这样就唯一地确定了n维空间中正负理想解的位置:
4) 计算每个评价对象与正负理想解的欧式距离.评价对象uj与正理想解A+、负理想解A-的距离分别为

5) 计算每个评价对象的综合效用值:

(21)
这样得到的综合效用值就是期望的综合评估值,ξj的实际意义就是攻击输入uj对所有输出产生的攻击增益的权衡值,也就是控制系统输入uj处的安全风险评估值.最后,选取这些指标构成控制系统物理层的安全风险评估向量:
ξ=(ξ1,ξ2,ξ3,…,ξn) .
(22)
式中:风险评估值ξj的取值始终在区间[0,1.0]内,因此有一个统一的标准,其越大说明输入uj的安全风险越大.
3.2评估算法时间复杂度分析
为了保证实时对系统安全风险进行评估,需要了
解工业对象的实时工作点,从而获得对象的开环传递函数,进而估算评估算法的时间复杂度问题.算法时间复杂度主要包括2个部分:闭环增益矩阵P计算和TOPSIS方法计算,并且都集中在矩阵运算中.
1) 闭环增益矩阵P时间复杂度分析.
一般来说,计算n阶矩阵的乘法和求逆所需的时间复杂度都是o(n3),因此,当根据开环稳态增益矩阵K求得RGA的复杂度为
t1(n)=o(n3)+o(n3);
另外还需要求出n2-n个n-1阶新RGA矩阵,其复杂度为
t2(n)=(n2-n){o[(n-1)3]+o[(n-1)3]}.
2) TOPSIS方法时间复杂度分析.
一般来说,计算n阶矩阵与向量的乘法所需的时间复杂度都是o(n2).对于TOPSIS的每一步计算所需的时间复杂度分别为t3(n)=n×o(n)、t4(n)=o(n2)、t5(n)=n×o(n)、t6(n)=o(n2)、t7(n)=o(n).从而可得整个评估算法的时间复杂度为
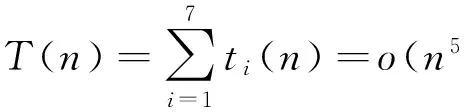
(23)
可以看出,整个评估算法的复杂度集中在闭环攻击增益矩阵的计算中.
4仿真结果及分析
为了形象地观察1.2节所述的攻击模型对MIMO控制系统的影响效果,并验证闭环攻击增益矩阵的正确性,考虑 Huang等[24]所使用的简化后的精馏塔过程模型:
[ΔT,ΔP,ΔL]T=G(s)·[ΔQB,ΔD,ΔR]T.
该式是系统处于稳态后的小增益模型,Δ表示增量其余变量如下:输入控制量QB为再沸器热载,D为塔顶馏出量,R为回流比;输出量T为控制塔板温度,P为控制塔内压强,L为回流釜液位.该模型可以模型简化为
[y1,y2,y3]T=G(s)·[u1,u2,u3]T.
(24)
其中,开环传递函数为
根据G(s)可以得到稳态增益矩阵K、相对增益阵列Λ:
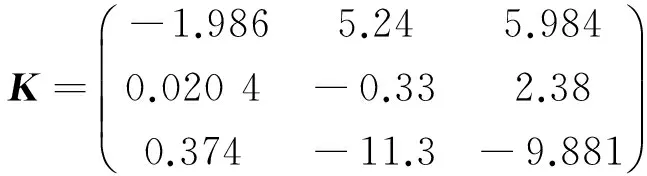

根据RGA配对规则[25],选择QB-T、P-R、L-D,即y1-u1、y2-u3、y3-u2构成回路进行闭环控制,控制器都采用比例积分(proportion-integration,PI)控制器,控制系统的结构如图2所示.
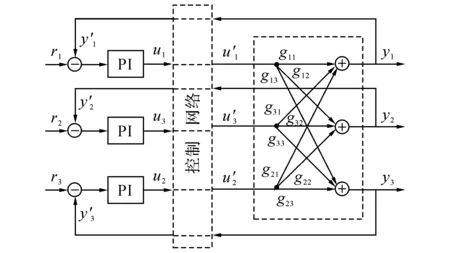
图2 精馏塔控制系统示意图Fig.2 Schematic diagram of rectifying tower control system
根据定理2,可以求出闭环攻击增益矩阵:
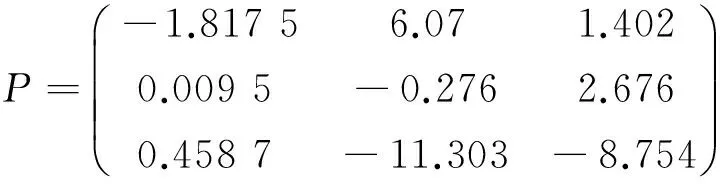
(25)
4.1闭环攻击矩阵验证
假设系统初始状态均为零,在t=0时刻给定参考输入,幅值分别为1、2、3的阶跃信号.设定在t>5 000 s之后,攻击行为才发生,攻击强度都是在t=5 000 s时刻输入的基础上附加相同的攻击增量:
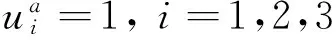

图3 不同攻击输入下目标输出随时间变化曲线Fig.3 History curve of target output under separated attack
根据单一变量原则,先选定一个输出作为攻击目标,再分别选取u1、u2、u3作为攻击点,绘制该输出随时间的变化曲线,仿真结果如图3所示.从定性角度看,当y1是与物理安全相关的变量时,攻击输入u2对y1的影响最大,这与矩阵P的第一行元素反映的规律是一致的.定量分析攻击后稳态输出y1,分别为-0.817 6、7.071 0、2.403 2,因此不同攻击输入对输出y3的闭环增益分别为-1.817 6、6.071 0、1.403 2,与矩阵P的第三行元素相同.图3(b)和(c)的分析结果相同,因此,仿真结果从定性和定量的角度均验证了闭环攻击增益矩阵提出的正确性.g12(s)中存在大延迟和大时滞环节,控制器没有采用微分环节,因此输出y1的响应存在超调和调节时间长的现象.
4.2安全风险评估
针对控制塔板温度T、控制塔内压强P、回流釜液位L对系统安全的影响程度,不妨选取权重矩阵为

根据第4章中提出的安全风险评估办法,可以得到该控制系统的安全风险评估向量:
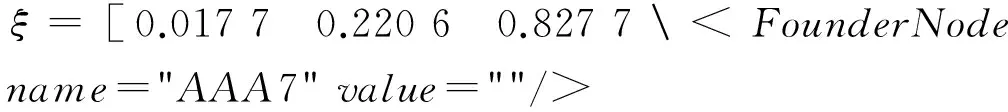
(26)
可以看出,输入u3(即回流比R处)的安全风险最高,其次是塔顶馏出量D,安全风险最低的是再沸器热载QB.因此,控制回流比R的相关设备,如:PLC、控制电机、阀门等,需要采用安全防护等级和可靠性较高的设备,而且控制网络中对应的信息通道也需要采取一定的信息安全措施.
5结语
本文提出了一种评估工业控制系统物理层安全风险的有效方法.该评估方法能较全面地结合工业被控对象的客观属性,科学合理地量化评估工业控制系统物理层中潜在的安全风险.但是,本文在工业控制系统安全风险评估问题上只考虑了物理层对象的安全风险,并没有考虑信息层,而且在权重向量W的选取上会出现“一票否决”问题.因此,如何结合信息层的风险来对工业控制系统进行全面的安全风险评估是下一步研究的方向.
参考文献 (References):
[1]STOUFFERK,FALCOJ,SCARFONEK.Guidetoindustrialcontrolsystems(ICS)security[J]. NIST special publication, 2011,800(82):16.
[2] ZHU Q, BASAR T. Game-theoretic methods for robustness, security, and resilience of cyberphysical control systems: games-in-games principle for optimal cross-layer resilient control systems [J]. Control Systems, IEEE, 2015, 35(1): 46-65.
[3] TEIXEIRA A, PEREZ D, SANDBERG H, et al. Attack models and scenarios for networked control systems [C] ∥ Proceedings of the 1st international conference on High Confidence Networked Systems. Beijing: ACM, 2012: 55-64.
[4] TURK R J. Cyber incidents involving control systems [R]. Idaho National Engineering and Environmental Laboratory, 2005.
[5] REED T. At the abyss: an insider’s history of the cold war [M]. New York: Presidio Press, 2007.
[6] SLAY J, MILLER M. Lessons learned from the maroochy water breach [M]. Berlin: Springer US, 2007, 253: 73-82.
[7] IGURE V M, LAUGHTER S A, WILLIAMS R D. Security issues in SCADA networks [J]. Computers and Security, 2006, 25(7): 498-506.
[8] OMAN P, SCHWEITZER E, FRINCKE D. Concerns about intrusions into remotely accessible substation controllers and SCADA systems [C]∥Proceedings of the Twenty-Seventh Annual Western Protective Relay Conference. Washington:WPRC, 2000, 160.
[9] HALPERIN D, et al. Pacemakers and implantable cardiac defibrillators: Software radio attacks and zero-power defenses [C] ∥ Security and Privacy, IEEE Symposium on. California: IEEE, 2008: 129-142.
[10] GREENGARD S. The new face of war [J]. Communications of the ACM, 2010, 53(12): 20-22.[11] CHEN T. Stuxnet, the real start of cyber warfare?[Editor’s Note] [J]. Network, IEEE, 2010, 24(6): 2-3.
[12] FIDLER D P. Was stuxnet an act of war? decoding a cyber attack [J]. IEEE Security and Privacy, 2011, 9(4): 56-59.
[13] FUBEERF. The secret of stuxnet [EB/OL]. (2015-08-04). [2015-07-01]. http:∥www.freebuf.com/articles/system/19059.html.
[14] MO Y L, SINOPOLI B. Secure control against replay attacks [C]∥ 47th Annual Allerton Conference on Communication, Control, and Computing. Allerton: IEEE, 2009: 911-918.[15] CRDENAS A A, AMIN S, LIN Z S, et al. Attacks against process control systems: risk assessment, detection, and response [C] ∥Proceedings of the 6th ACM symposium on information, computer and communications security. Hong Kong: ACM, 2011: 355-366.
[16] KWON C, LIU W, HWANG I. Security analysis for cyber-physical systems against stealthy deception attacks [C] ∥ American Control Conference (ACC), 2013. Washington: IEEE, 2013: 3344-3349.
[17] TEIXEIRA A, SHAMES I, SANDBERG H, et al. A secure control framework for resource-limited adversaries [J]. Automatica, 2015, 51: 135-148.
[18] KHAKZAD N, KHAN F, AMYOTTE P. Safety analysis in process facilities: comparison of fault tree and bayesian network approaches [J]. Reliability Engineering and System Safety, 2011, 96(8): 925-932.
[19] CUI X L, TAN X B, Z Y, et al. A Markov Game theory-based risk assessment model for network information system [C] ∥ 2008 International Conference on Computer Science and Software Engineering. Wuhan: IEEE, 2008: 1057-1061.
[20] HAWRYLAK P J, HANEY M, PAPA M, et al. Using hybrid attack graphs to model cyber-physical attacks in the smart grid [C]∥Resilient Control Systems (ISRCS) 2012 5th International Symposium on. Utah: IEEE, 2012: 161-164.
[21] ALVARO A, CRDENAS A A, SAURABH A. Research challenges for the security of control systems [C]∥Proceedings of the 3rd Conference on Hot Topics in Security, California: HOTSEC,2008:1-6.
[22] BRISTOL E. On a new measure of interaction for multivariable process control [J]. IEEE transactions on automatic control, 1966,11(1): 133-134.
[23] HWANG C L, LAI Y J, LIU T Y. A new approach for multiple objective decision making [J]. Computers and Operations Research, 1993, 20(8): 889-899.
[24] HUANG H P, OHSHIMA M, HASHIMOTO I. Dynamic interaction and multiloop control system design [J]. Journal of Process Control, 1994, 4(1): 15-27.
[25] GAGNEPAIN J P, SEBORG D E. Analysis of process interactions with applications to multiloop control system design [J]. Industrial and Engineering Chemistry Process Design and Development, 1982, 21(1): 5-11.
DOI:10.3785/j.issn.1008-973X.2016.03.025
收稿日期:2015-08-04.
基金项目:国家自然科学基金资助项目(61223004);工业控制系统安全脆弱性分析与建模的理论与应用研究.
作者简介:梁耀(1993-),男,硕士生,从事工业控制系统安全分析研究,ORCID:0000-0002-5505-0633.E-mail:liangyaoxp@zju.edu.cn 通信联系人:冯冬芹,男,教授,博导,ORCID:0000-0002-3034-0933.E-mail:dqfeng@iipc.zju.edu.cn
中图分类号:TP 11
文献标志码:A
文章编号:1008-973X(2016)03-08-0589
Security risks assessment for physical layer of industrial control system based on attack gain
LIANG Yao, FENG Dong-qin
(InstituteofCyber-SystemsandControl,StateKeyLaboratoryofIndustrialControlTechnology,ZhejiangUniversity,Hangzhou310027,China)
Abstract:Inspired by variable pairing applied in the multiple-input and multiple-output (MIMO) system, an indicator was raised to measure the sensitivity of each output to different attack inputs under close-loop conditions based on relative gain array (RGA), such as close-loop attack gain array. Combined with technique for order preference by similarity to ideal solution (TOPSIS), an assessment method was proposed to quantitatively analyze security risks in the physical layer of an industrial control system. The attack impact was presented intuitively, the correctness of close-loop attack gain array above was verified, and the area related to reflux ratio was found at most risks in the physical layer based on the case study of a rectifying tower testbed. Results show that the proposed assessment method can combine objective attributes of the controlled object more comprehensively, making a quantitative asessment of potential security risks that exist in the physical layer of an industrial control system scientifically and reasonably.
Key words:security risks assessment; physical layer of an industrial control system; multiple-input and multiple-output (MIMO) system; relative gain array (RGA); close-loop attack gain array; TOPSIS
