一种有效的地震动速度时程时域特性分析方法
2016-07-28赵国臣徐龙军谢礼立
赵国臣, 徐龙军, 谢礼立
哈尔滨工业大学(威海)土木工程系, 山东威海 264209
一种有效的地震动速度时程时域特性分析方法
赵国臣, 徐龙军*, 谢礼立
哈尔滨工业大学(威海)土木工程系, 山东威海264209
摘要在分析特殊型地震动如近场脉冲型地震动或远场类谐和地震动时,研究和设计人员更关注于地震动的时域特性.鉴于目前尚不具有一种成熟的用于分析地震动时域特性的方法,在研究中通常采用肉眼辨别地震动.但在肉眼辨别的过程中并没有定量的指标描述地震动的特性,因此这种方法容易引入人为的主观性误差.地震动的时域特性主要指地震动的振动周期和强度随时间的变化情况.如有一种定量描述这种变化的方法便能消除肉眼辨别中引入的主观性误差.为解决该问题,本文提出了一种简便、有效的分析地震动速度时程时域特性的速度零点法ZVPM(Zero Velocity Point Method).采用这种方法可以定量地分析地震动速度时程的振动周期和强弱程度随时间的变化情况,并可以通过定义的幅值参数、周期参数和相位参数获取等效的地震动速度时程.鉴于脉冲型地震动对结构具有特殊的破坏作用,本文采用速度零点法分析了24条典型的强脉冲型地震动,并基于速度零点法提出了一种简便的脉冲周期计算方法.为便于工程设计人员快速地获取本文所选脉冲型地震动的等效速度脉冲,文中给出了每一条地震动等效速度脉冲的数学表达式.
关键词时域分析方法; 地震动特性; 脉冲型地震动; 等效速度脉冲; 脉冲特性
1引言
地震动记录是认识地震,分析地震的重要数据资料,也是进行建筑结构和工程设施等抗震设计的主要依据(胡聿贤, 2006).在进行地震动反应谱分析、地震危险性分析和结构易损性分析等研究时,均需要选取一组具有代表性的地震动记录.在传统的研究中主要依据地震动的参数如幅值、频谱和持时等选取地震动.然而一些特殊的地震动虽然其参数之间相差不大,但结构在其作用下的反应却相差较大.为解决这个问题,通常采用肉眼辨别地震动.但在肉眼辨别过程中缺乏定量的评价指标,易引入人为的主观性误差.例如,在断层破裂方向性效应的影响下,近场地震动中常含有一个明显的速度脉冲,在研究中通常称此类地震动为近场脉冲型地震动(Somerville et al., 1997; Somerville, 2003).在面波和场地的共同作用下,远场软土场地地震动的时程后期常含有多个明显的长周期循环脉冲,在研究中通常称此类地震动为远场类谐和地震动(徐龙军等, 2008; 李雪红等, 2014).虽然肉眼可以辨别地震动中是否存在速度脉冲或者谐和波,但并不能定量地判别速度脉冲或者谐和波的强弱以及周期,仍需经繁琐的计算后才能给出最终的评价.当地震动的脉冲特性或谐和波不明显时,不同的学者所选取的地震动记录之间必然存在很大的差异.在选取这些特殊型地震动时,研究和设计人员更关注于地震动的时域特性.目前虽有很多成熟的时频分析方法,如小波分析等,已被引入到地震动的研究中(Baker, 2007;Ghahari et al., 2010; Vassiliou and Makris, 2011; 陈红等, 2011; 谢俊举等, 2012; 赵国臣等, 2013; Lu and Panagiotou, 2014).但这些方法均涉及复杂的数学理论,并不便于在工程实践中具体操作.地震动的时域特性主要表现为地震动的振动周期和强弱程度随时间的变化情况.如有一种能够定量描述这种变化的方法,便能解决肉眼辨别过程中的不足.
为解决上述问题,本文基于三角函数的性质提出了一种能够有效分析地震动速度时程时域特性的速度零点法ZVPM(Zero Velocity Point Method).采用这种方法能够有效地检测出地震动速度时程中的每一个循环振动区间,并定义了用于描述地震动速度时程在每一个循环振动区间的周期参数和强弱程度的功率参数.由此,通过这种方法可以定量地分析地震动速度时程的振动周期和振动强度随时间的变化情况.此外,本文基于速度零点法提出了一种用于等效地震动速度时程的方法,并给出了幅值、相位角和周期的计算公式.鉴于脉冲型地震动的特殊性,本文以24条典型的脉冲型地震动为例讨论了速度零点法在地震动时域特性分析中的有效性.脉冲周期是脉冲型地震动的重要参数之一.本文采用速度零点法检测到的速度脉冲的振动区间的长度作为脉冲周期,并对比了速度零点法、速度谱方法以及Shahi和Baker(2014)方法所求取的脉冲周期间的差异.最后本文给出了所选24条脉冲型地震动等效速度脉冲的数学表示式,以期能为断层区抗震设计中速度脉冲的选取等相关工作的理论研究和工程实践提供有价值的参考资料.
2速度零点法及相关参数
2.1数学原理
在研究中一般认为地震动加速度时程围绕零轴,即Acc=0振动,并且加速度时程的初始值并不一定为0.因此,一个频率为ω,幅值为A和相位角为θ的地震动加速度模型可以假定为
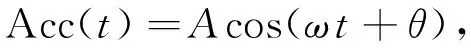
(1)
则,与其相对应的速度模型为
(2)
定义参数P:P=sign[Acc·Vel]·|Acc|·sign[Acc(1)]-Acc,
(3)其中sign(·) 是符号函数(当x>0时,sign(x)=1;当x=0时,sign(x)=0;当x<0时,sign(x)=-1);Acc(1)是加速度时程中的第一个非零值.
定义速度模型从0开始逐渐增大到最大值(或逐渐减小至最小值),然后返回0点,再减小至最小值(或再增大至最大值),最后返回0点的过程为速度模型的一个循环振动区间.定义ti(i=1,2,3,…)是速度模型第i个等于0的点.则Ik=[t2k-1, t2k+1] (k=1,2,3,…)是速度模型的第k个循环振动区间.显然,t=0是速度模型第一个等于0的点,I1=[t1,t3]是速度模型的第一个循环振动区间.如图1(a—d)所示,当θ∈{-π≤θ≤π,θ≠±0.5π}时,在区间[t2k-1, t2k]内P=0,在区间[t2k,t2k+1]内P≠0.如图1(e—f)所示,当θ=±0.5π时,P一直等于0.因此,当θ≠±0.5π时,在任意一个给定的循环振动区
间内,首先P=0然后P≠0.
图2是日本Kobe地震PortIsland台站的加速度和速度时程曲线.如图所示,t1—t3和t3—t5是该地震动速度时程中两个相邻的循环振动区间.由计算知,在区间t1—t2内P=0,在区间t2—t3内P≠0,在区间t3—t4内P=0,在区间t4—t5内P≠0.由于地震动的速度时程不能一直大于0或者一直小于0,所以不会出现图1e和1f中,即θ=±0.5π时的情况.因此通过这种方法可以检测出地震动速度时程中所有的循环振动区间.鉴于这种方法通过检测速度为0的点,本文称这种方法为速度零点法ZVPM(ZeroVelocityPointMethod).
2.2几个重要的地震动参数
2.2.1周期参数
在周期荷载作用下,结构周期与荷载周期之间的比值是决定结构动力响应的主要参数之一.在传统的研究中一般仅采用一个宏观的参数描述地震动的周期,如地震动绝对加速度反应谱、相对速度反应谱、相对位移反应谱或傅里叶幅值谱的峰值周期.然而地震动的振动周期随时间的变化而变化.采用一个特定的参数并不能够描述这种变化情况.
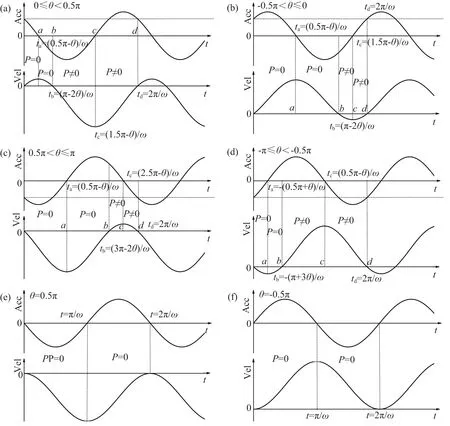
图1 参数P计算原理图(a) 0 ≤θ<0.5π; (b) -0.5π<θ≤0; (c) 0.5π<θ≤π; (d) -π≤θ<-0.5π; (e) θ=0.5π; (f) θ=-0.5π.Fig.1 Calculation schematic chart for parameter P
由上文分析知,地震动在第k个循环振动区间Ik的振动周期Tk即为该区间的长度.通过速度零点法便可以简便地求出地震动在每一个循环振动区间内的周期.虽然这种周期并不是地震动的瞬时周期,而是每一个循环振动区间的平均周期.但相对于采用一个特定的参数,这种方法能够描述地震动的振动周期在不同循环振动区间的变化情况.图3为两条地震动的Tk时程曲线.图3a所示地震动是一条典型的近断层脉冲型地震动,图中阴影区域为速度脉冲部分,图3b所示地震动是一条典型的远场类谐和地震动,图中阴影区域为谐和振动部分.为便于显示,图3a和3b中的速度时程均进行了调整.由图可知,通过速度零点法可以预估地震动在每一个循环振动区间内的周期.从图中可以定量地判别图3a所示地震动的脉冲周期约为2.5 s,图3b所示地震动谐和波的振动周期约为5 s.由此,通过本文方法无需繁琐的计算便可求出地震动在任意循环振动区间内的周期,这将为分析地震动的特性提供一种定量的指标,而非主观性判断.

图2 日本Kobe地震Port Island台站地震动加速度和速度时程Fig.2 Acceleration and velocity time histories of the ground motion recorded at the station of Port Island in Kobe, Japan earthquake
2.2.2强度参数
由图3知,Tk可以描述地震动在不同循环振动区间内的周期.但在各个循环振动区间内地震动的强弱程度并不一致.因此,需要一种可以描述地震动在每一个循环振动区间内强弱程度的参数.在研究中一般采用累积平方速度计算地震动的能量.由于地震动时程是离散数据,因此地震动的能量可以表示为
(4)
其中Δt是地震动时程的时间间隔;N是地震动时程中离散点的个数.
由此,地震动在循环振动区间Ik内的能量可以表示为
(5)
其中,Nk是地震动在循环振动区间Ik内的离散点的个数.
由于不同地震动的能量值之间有很大的差异,为消除这种差异,本文将Ek和E之间的比值定义为相对能量比,即
(6)
当速度幅值一致时,循环振动区间的周期越长,其相对能量比将越大.为消除周期的影响,本文采用相对能量比ERk和周期Tk之间的比值,即

图3 Tk时程曲线(a) 日本Kobe地震Port Island台站(脉冲型地震动); (b) 台湾集集地震ILA056台站(类谐和地震动).Fig.3 Tk time history(a) Port Island station in Kobe, Japan earthquake (Pulse-like ground motion);(b) ILA056 station in Chi-Chi, Taiwan earthquake (Harmonic-like ground motion).
(7)
EPk描述地震动在循环振动区间Ik内的强弱程度,并称这个参数为相对功率.可以证明地震动的相对功率在整个时程上的积分和为1.图4是图3所示两条地震动EPk的时程曲线.图4a和4b中阴影部分分别是速度脉冲和谐和波.为便于显示,图4中的速度时程也进行了调整,但所选取的调整系数与图3不同.由图知,通过EPk可以定量地描述地震动在不同循环振动区间内的强弱程度.图4a是典型的脉冲型地震动,因此在脉冲区间内的相对功率值较大.图4是典型的类谐和地震动,因此在谐和振动区间内的相对功率值较大.由图3a知地震动脉冲周期约为2.5 s,由图4a知速度脉冲的相对功率约为0.3,则速度脉冲的相对能量比约为0.75,即速度脉冲的能量约占地震动全部能量的75%,因此该地震动是强脉冲型地震动.由图4b知地震动中有5个连续的循环振动区间的相对功率均较大,因此该地震动具有5个循环振动的谐和波.结合图3可求出5个循环振动的谐和波的相对能量比约为0.8,即约占地震动全部能量的80%.由此,速度零点法提供了一种定量分析地震动强弱程度随时间变化的方法,这将为地震动的初步选取等研究工作提供科学的评判指标.
2.3等效地震动速度时程
根据式(2)知,在区间Ik内的地震动速度时程可以等效为
(8)
由图1可知:
(9)
因此
(10)
在本文中对地震动加速度时程作如下处理:
Acc=Acc·sign[Acc(1)],
(11)
其中Acc(1)是地震动加速度时程中的第一个非零值点.由图1知,经式(4)处理后,相位角θ∈(-0.5π,0.5π).
根据周期和频率间的关系,可求地震动在Ik区间内的圆频率为
(12)
由于在区间Ik内,地震动的速度时程类似于简谐波,因此地震动速度时程的幅值可以表示为
(13)
其中Vkmax和Vkmin分别是地震动速度时程在循环振动区间Ik内的最大值和最小值.
可以证明采用这种方法求得的等效速度时程在任意一个循环振动区间内的初始值和结束值均为0,因此采用这种方法求得的等效速度时程是连续的.图5为采用这种方法计算得到的等效速度时程与原始速度时程的对比图.由图知,等效的速度时程能够较好地反映原始速度时程的特性.在地震动的相关研究中有时需要获取等效速度脉冲或谐和波,本文的方法便可为这些研究工作提供一种简便、可行的途径.
由上述分析知,采用速度零点法可以检测出地震动中的每一个循环振动区间,并可以求取每一个循环振动区间的周期参数、强度参数、幅值参数和相位参数.通过这些参数可以定量地分析地震动的周期和强度随时间的变化情况,并可以通过所定义的参数获得等效的速度时程.需要指出的是,通过其他方法同样可以检测出速度值为0的点,但这些方法不能识别循环振动区间的起止点,也不能求出地震动在循环振动区间内的相位角.因此,本文所提出的速度零点法与传统的检测零点的方法是有区别的.
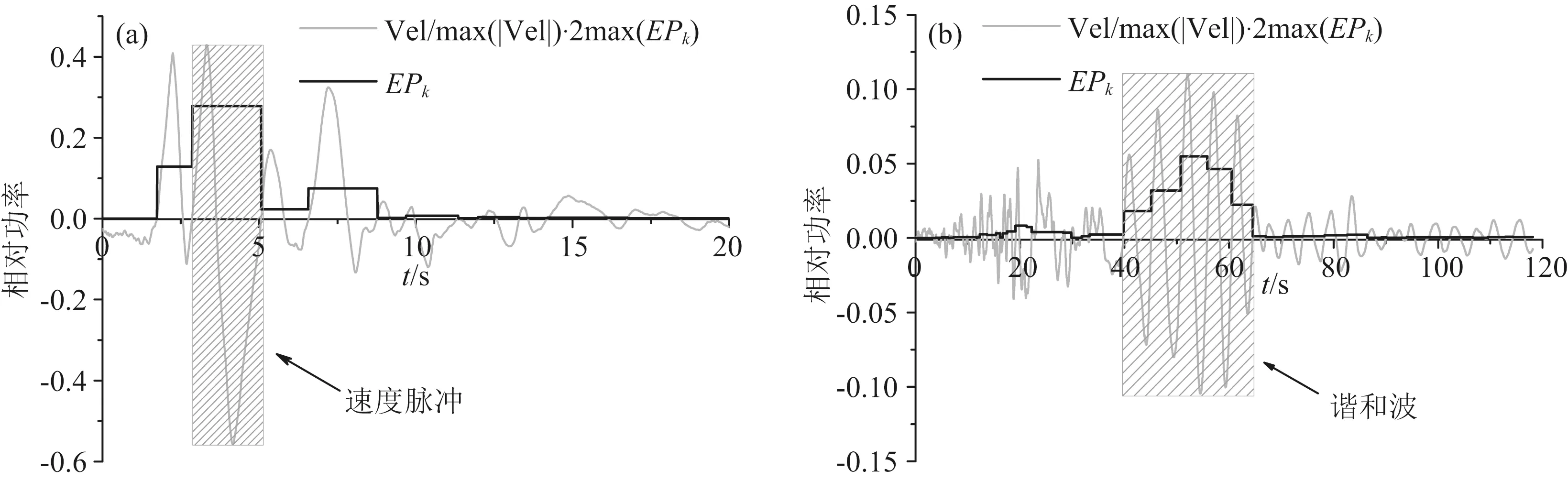
图4 EPk时程曲线(a) 日本Kobe地震Port Island台站(脉冲型地震动); (b) 台湾集集地震ILA056台站(类谐和地震动).Fig.4 EPk time history(a) Port Island station in Kobe, Japan earthquake (Pulse-like ground motion); (b) ILA056 station in Chi-Chi, Taiwan earthquake (Harmonic-like ground motion).
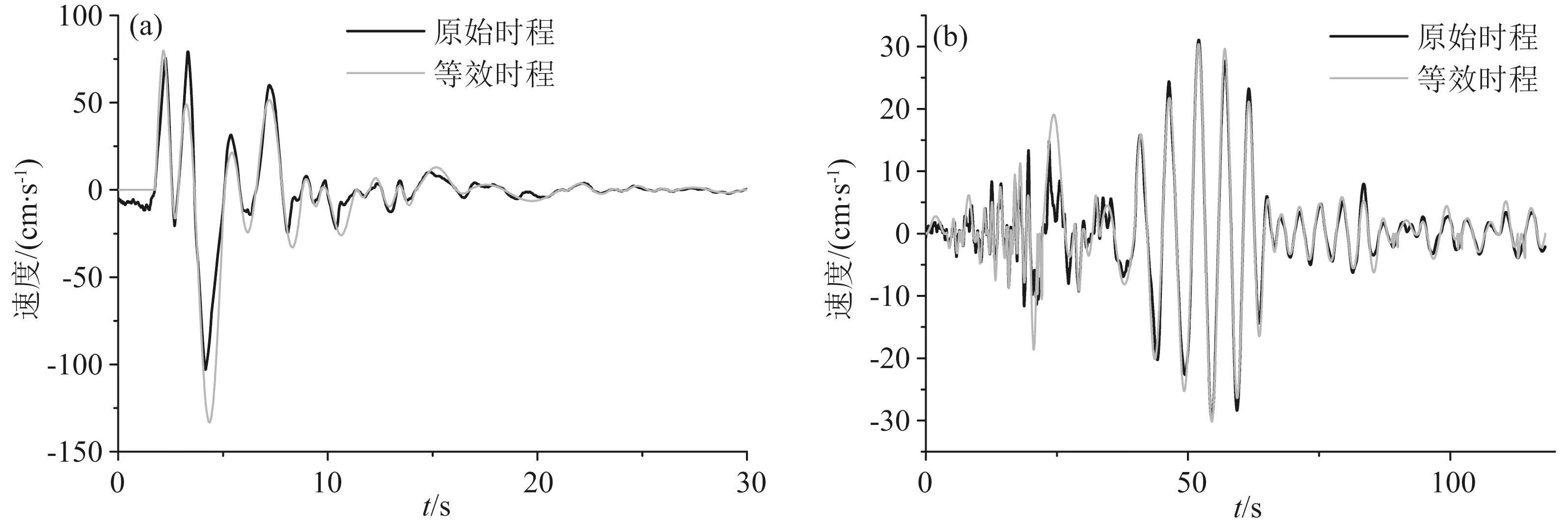
图5 等效速度时程与原始速度时程对比图(a) 日本Kobe地震Port Island台站(脉冲型地震动); (b) 台湾集集地震ILA056台站(类谐和地震动).Fig.5 Comparison for equivalent velocity time histories with original velocity time histories(a) Port Island station in Kobe, Japan earthquake (Pulse-like ground motion); (b) ILA056 station in Chi-Chi, Taiwan earthquake (Harmonic-like ground motion).
3采用速度零点法分析脉冲型地震动的特性
脉冲型地震动具有高速度、高位移幅值,短持时和长周期的特性.研究表明结构在该类地震动作用下需要具有更高的延性和强度需求(Halletal., 1995;Iwan, 1997;AlaviandKrawinkler, 2004;MakrisandBlack, 2004;Mavroeidisetal., 2004;Akkaretal., 2005;LucoandCornell, 2007; 赵国臣等, 2015).本节以脉冲型地震动为例,讨论速度零点法在分析地震动时域特性中的有效性,并希望通过速度零点法获取一组典型的脉冲型地震动的参数为工程设计人员选取速度脉冲时提供有价值的参考资料.为此,本文在前人研究的基础上选取了24条典型的强脉冲型地震动记录.本文所选地震动的震级均在6级以上,断层距在15km以内,峰值速度PGV大于30cm·s-1,速度时程中均含有明显的速度脉冲.所选地震动记录均从PEER强地震动数据库(http:∥ngawest2.berkeley.edu/)下载得到.台站和地震的详细信息见表1.
3.1脉冲周期
脉冲周期和脉冲幅值是描述脉冲型地震动脉冲特性最主要的两个参数.一般采用峰值速度PGV表示脉冲幅值,但对于脉冲周期的定义尚存在很大的争议.有的采用零交法计算脉冲周期,有的通过最优化方法计算等效脉冲然后求取脉冲周期(Menun and Fu, 2002; Mavroeidis and Papageorgiou, 2003; Bray and Rodriguez-Marek, 2004; Akkar et al., 2005).Shahi和Baker(2014)采用连续小波变换系数所对应的尺度求取脉冲周期.目前在国内外的相关研究中普遍认可采用速度反应谱的峰值周期作为脉冲周期.地震动的速度反应谱是多种频率成分共同作用的结果.当地震动频率成分较为复杂时,速度反应谱可能会出现多个幅值相近的峰值点.因此,采用速度谱法并不易于准确确定脉冲周期,所确定的脉冲周期也不直观.
由上文分析知,速度零点法能够检测地震动中的每一个循环振动区间,同样也可以检测速度脉冲的振动区间.本文将速度零点法检测到的速度脉冲的振动区间的长度作为脉冲周期.这样所确定的脉冲周期非常直观,物理意义也更明确.图6对比分析了采用速度零点法计算得到的脉冲周期TP、Shahi和Baker(2014)计算得到的脉冲周期TS和速度谱峰值法计算得到的脉冲周期TV.由图6a知,采用Shahi和Baker(2014)计算得到的脉冲周期TS的值较大,采用速度谱方法计算得到的脉冲周期TV的值较小,本文方法计算得到的脉冲周期TP的值较为适中.图6b为三种周期的回归关系图.由图知TS约为TV的1.1倍,TP约为TV的1.03倍,且TP与TV之间差的平方和小于TS与TV之间差的平方和.
3.2等效速度脉冲
为系统分析脉冲型地震动的脉冲特性,许多学者采用简化的速度脉冲模型等效地震动中的速度脉冲(Makris, 1997; Krawinkler and Alavi, 1998, Alavi and Krawinkler, 2000; Menun and Fu, 2002; Mavroeidis and Papageorgiou, 2003),或者采用分解方法分离地震动中的速度脉冲(Baker, 2007;Ghahari et al., 2010; Vassiliou and Makris, 2011; Lu and Panagiotou, 2014).这些方法对于认识该类地震动的脉冲特性提供了非常有价值的参考资料.但这些方法大都涉及到较为复杂的数学理论,并不便于在工程实践中应用.

表1 脉冲型地震动台站信息表
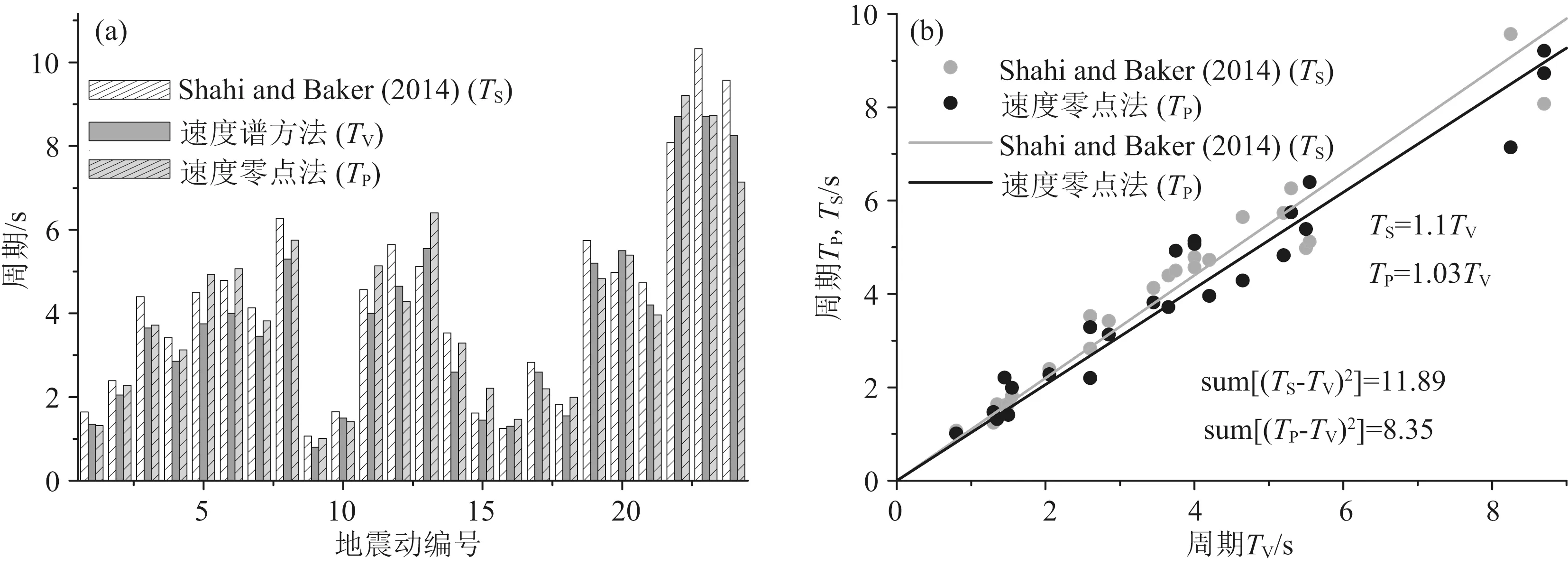
图6 三种周期(TS、TP和TV)对比(a) TS、TP和TV对比图; (b) TS与TV、TP与TV回归关系图.Fig.6 Comparison for the three kinds of period (TS、TP and TV)(a) Comparison for TS、TP and TV; (b) Regression relationship for TS and TV, TP and TV.

(14)其中VP为脉冲幅值;TP为脉冲周期;θP为脉冲相位角.
图7展示了24条脉冲型地震动的速度时程及采用速度零点法获取的等效速度脉冲.由图知,对于大多数地震动采用本文方法得到的等效脉冲均能较好地反映原始脉冲的特性.表1中给出了24条脉冲型地震动等效速度脉冲的参数.当进行断层区的抗震设计并需要考虑脉冲型地震动的影响时,若工程设计人员预选用本文中的脉冲型地震动记录,便可以根据表1中给出的参数快速地获取地震动的等效速度脉冲以用于相关的分析工作.速度零点法仅采用一个循环振动的正弦波等效速度脉冲,因此等效脉冲只能粗略反映原始脉冲的特征.但这种方法确实可以给工程设计人员提供一种简便可行的获取速度脉冲的途径.本文主要目的是探究一种有效的地震动的时域特性分析方法,而非获取脉冲型地震动的等效速度脉冲.当在理论研究中需获取等效速度脉冲时,仍需要对比前人所提出的几种等效速度脉冲方法,以判别哪种方法的等效效果更好.本文对此不作过多的讨论.

图7 24条脉冲型记录的等效速度脉冲Fig.7 Equivalent velocity pulse for the 24 pulse-like ground motions
4结论
为定量分析地震动的时域特性,本文提出了一种简便、有效的地震动速度时程时域特性分析方法,并定义了几种描述地震动速度时程时域特性的参数,最后采用这种方法分析了24条典型强脉冲型地震动的特性.本文的研究工作主要得到了以下几个方面的认识:
(1) 采用速度零点法可以有效地检测地震动速度时程中的每一个循环振动区间,并可以求取每一个循环振动区间的周期参数、强度参数、幅值参数和相位参数.通过这种方法可以定量地分析地震动速度时程的振动周期和强弱程度随时间的变化情况,这将为地震动的初步选取等研究工作提供一种定量的评判指标.
(2) 本文基于速度零点法提出了一种有效的用于等效地震动速度时程的方法,并可以根据所定义的参数获取等效速度时程的数学表达式.在地震动的相关研究中有时需要获取等效速度脉冲或谐和波,本文方法便可为这些研究工作提供一种简便、可行的途径.
(3) 本文基于速度零点法,采用脉冲型地震动速度脉冲循环振动区间的长度作为脉冲周期.虽然采用本文方法计算得到的脉冲周期与采用速度谱方法计算得到的脉冲周期相差不大,但本文方法比较直观,所求周期的概念更易于理解,且不需经过复杂的数学计算就可以求得,非常便于地震动的初步选取等相关工作.
(4)本文采用速度零点法获取了24条典型强脉冲型地震动的等效速度脉冲并给出了具体的数学表达式.在进行断层区的抗震设计时,若工程设计人员预选用本文中的脉冲型地震动记录,便可以根据文中给出的参数快速地获取地震动的等效速度脉冲以用于相关的分析工作.
References
Akkar S, Yazgan U, Gülkan P. 2005. Drift estimates in frame buildings subjected to near-fault ground motions.JournalofStructuralEngineering, 131(7): 1014-1024.
Alavi B, Krawinkler H. 2000. Effects of near-fault ground motions on frame structures.Technical Report 138.Stanford, California: John A Blume Earthquake Engineering Center, Stanford University. Alavi B, Krawinkler H. 2004. Behavior of moment-resisting frame structures subjected to near-fault ground motions.EarthquakeEngineering&StructuralDynamics, 33(6): 687-706.
Baker J W. 2007. Quantitative classification of near-fault ground motions using wavelet analysis.BulletinoftheSeismologicalSocietyofAmerica, 97(5): 1486-1501.
Bray J D, Rodriguez-Marek A. 2004. Characterization of forward-directivity ground motions in the near-fault region.SoilDynamicsandEarthquakeEngineering, 24(11): 815-828.
Chen H, Peng Z M, Wang J, et al. 2011. Spectral decomposition of seismic signal based on fractional Gabor transform and its application.ChineseJournalofGeophysics(in Chinese), 54(3): 867-873, doi:10.3969/j.issn.0001-5733.2011.03.028.
Ghahari S F, Jahankhah H, GhannadM A. 2010. Study on elastic response of structures to near-fault ground motions through record decomposition.SoilDynamicsandEarthquakeEngineering, 30(7): 536-546. Hall J F, Heaton T H, Halling M W, et al. 1995. Near-source ground motion and its effects on flexible buildings.EarthquakeSpectra, 11(4): 569-605.
Hu Y X. 2006. Earthquake Engineering (in Chinese).2nd ed. Beijing:Seismological Press.
Iwan W D. 1997. Drift spectrum: Measure of demand for earthquake ground motions.JournalofStructuralEngineering, 123(4): 397-404. Krawinkler H, Alavi B. 1998. Development of improved design procedures for nearfault ground motions. ∥SMIP98, Seminar on Utilization of Strong Motion Data.Oakland, CA.
Li X H, Wang W K, Wu D, et al. 2014. The bounded method and characteristics analysis for long-period ground motions.JournalofVibrationEngineering(in Chinese), 27(5): 685-692.
Lu Y, Panagiotou M. 2014. Characterization and representation of near-fault ground motions using cumulative pulse extraction with wavelet analysis.BulletinoftheSeismologicalSocietyofAmerica, 104(1): 410-426.
Luco N, Cornell C A. 2007. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions.EarthquakeSpectra, 23(2): 357-392.
Makris N. 1997. Rigidity-plasticity-viscosity: Can electrorheological dampers protect base-isolated structures from near-source ground motions.EarthquakeEngineering&StructuralDynamics, 26(5): 571-591. Makris N, Black C J. 2004. Dimensional analysis of bilinear oscillators under pulse-type excitations.JournalofEngineeringMechanics, 130(9): 1019-1031. Mavroeidis G P, Papageorgiou A S. 2003. A mathematical representation of near-fault ground motions.BulletinoftheSeismologicalSocietyofAmerica, 93(3): 1099-1131.
Mavroeidis G P, Dong G, Papageorgiou A S. 2004.Near-fault ground motions, and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems.EarthquakeEngineering&StructuralDynamics, 33(9): 1023-1049.
Menun C, Fu Q. 2002. An analytical model for near-fault ground motions and the response of SDOF systems.∥Proceedings of the 7th U.S. National Conference on Earthquake Engineering.Boston, Massachusetts:Mira Digital Publishing.
Shahi S K, Baker J W. 2014. An efficient algorithm to identify strong-velocity pulses in multicomponent ground motions.BulletinoftheSeismologicalSocietyofAmerica, 104(5): 2456-2466.
Somerville P G, Smith N F, Graves R W, et al. 1997.Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity.SeismologicalResearchLetters, 68(1): 199-222.
Somerville P G. 2003.Magnitude scaling of the near fault rupture directivity pulse.PhysicsoftheEarthandPlanetaryInteriors, 137(1-4): 201-212. Vassiliou M F, Makris N. 2011. Estimating time scales and length scales in Pulse like earthquake acceleration records with wavelet analysis.BulletinoftheSeismologicalSocietyofAmerica, 101(2): 596-618.
Xie J J, Wen Z P, Li X J, et al. 2012. Analysis of velocity pulses for near-fault strong motions from the Wenchuan earthquake based on wavelet method.ChineseJournalofGeophysics(in Chinese), 55(6): 1963-1972, doi:10.6038/j.issn.0001-5733.2012.06.017.
Xu L L, Hu J J, Xie L L. 2008. On characteristics of ground motion parameters for special long-period ground motions.JournalofEarthquakeEngineeringandEngineeringVibration(in Chinese), 28(6): 20-27.
Zhao G C, Xu L L, Xie L L. 2013. On near-fault ground motion characteristics through multi-scale method.ChineseJournalofGeophysics(in Chinese), 56(12): 4153-4163, doi:10.6038/cjg20131219.
Zhao G C, Xu L L, Xie L L. 2015. On inelastic response spectra of pulse-type ground motion based on decomposed method.ChineseJournalofGeophysics(in Chinese), 58(8): 2962-2974, doi:10.6038/cjg20150828.
附中文参考文献
陈红, 彭真明, 王峻等. 2011. 地震信号分数阶Gabor变换谱分解方法及应用. 地球物理学报, 54(3): 867-873, doi:10.3969/j.issn.0001-5733.2011.03.028.
胡聿贤. 2006. 地震工程学. 2版. 北京: 地震出版社.
李雪红, 王文科, 吴迪等. 2014. 长周期地震动的特性分析及界定方法研究. 振动工程学报, 27(5): 685-692.
谢俊举, 温增平, 李小军等. 2012. 基于小波方法分析汶川地震近断层地震动的速度脉冲特性. 地球物理学报, 55(6): 1963-1972, doi:10.6038/j.issn.0001-5733.2012.06.017.
徐龙军, 胡进军, 谢礼立. 2008. 特殊长周期地震动的参数特征研究. 地震工程与工程振动, 28(6): 20-27.
赵国臣, 徐龙军, 谢礼立. 2013. 基于多尺度分析方法的近断层地震动特性分析. 地球物理学报, 56(12): 4153-4163, doi:10.6038/cjg20131219.
赵国臣, 徐龙军, 谢礼立. 2015. 基于分解方法的脉冲型地震动非弹性反应谱分析. 地球物理学报, 58(8): 2962-2974, doi:10.6038/cjg20150828.
(本文编辑胡素芳)
基金项目国家自然科学基金重点项目(51238012),山东省科技发展计划(2014GSF122001)和山东省蓝色经济区工程建设与安全协同创新中心资助.
作者简介赵国臣,男,博士研究生,主要从事防灾减灾工程研究. E-mail: zgc011@126.com *通讯作者徐龙军,男,教授,主要从事防灾减灾工程研究. E-mail: xulongjun80@163.com
doi:10.6038/cjg20160619 中图分类号P631, P315
收稿日期2015-06-18,2016-03-11收修定稿
An effective method for investigating the time-domain characterizations of ground motion velocity time history
ZHAO Guo-Chen, XU Long-Jun*, XIE Li-Li
DepartmentofCivilEngineering,HarbinInstituteofTechnologyatWeihai,ShandongWeihai264209,China
AbstractResearchers and designers will more prefer to learn the time-domain characterizations of ground motions when selecting special ground motions such as pulse-like ground motions or harmonic-like ground motions. In consideration of that there is no mature method to investigate ground motion characterization in time-domain, visual identification is always used. But there is no quantitative index used for describing ground motion characterization in the process of visual identification, so subjectivity errors caused by human are often involved. Ground motion time-domain characterization mainly indicates the variation of vibration period and the intensity of ground motions with time history. If there is a quantitative method to describe the variation, then the subjectivity errors can be eliminated. To solve the problem, this article proposed a simple and effective method which is named as Zero Velocity Point Method (ZVPM) to analyze the time-domain characterizations of ground motions. This method could quantitatively analyze the variation of vibration period and the intensity of ground motions with time history. And the equivalent velocity time-history can be obtained by the predefined amplitude parameter, period parameter and phase parameter. Considering the special destructive effects of pulse-like ground motions to structures, this article analyzed 24 typical pulse-like ground motions and proposed a simple method to calculate the pulse period based on Zero Velocity Point Method. In order to quickly obtain the equivalent velocity pulse of the ground motions utilized in this paper for engineering designers, the arithmetic expression of equivalent velocity pulse for each ground motion is given out.
KeywordsTime-domain analysis method; Ground motion characterization; Pulse-like ground motion; Equivalent velocity pulse; Impulsive characteristic
赵国臣, 徐龙军, 谢礼立. 2016. 一种有效的地震动速度时程时域特性分析方法. 地球物理学报,59(6):2138-2147,doi:10.6038/cjg20160619.
Zhao G C, Xu L J, Xie L L. 2016. An effective method for investigating the time-domain characterizations of ground motion velocity time history.ChineseJ.Geophys. (in Chinese),59(6):2138-2147,doi:10.6038/cjg20160619.
