过套管电阻率测井的地层电阻率快速反演算法

刘福平， 王安玲， 刘华群， 杨长春

1 北京印刷学院， 北京　102600　2 中国科学院地质与地球物理研究所， 北京　100029



过套管电阻率测井的地层电阻率快速反演算法

刘福平1, 2， 王安玲1， 刘华群1， 杨长春2

1 北京印刷学院， 北京1026002 中国科学院地质与地球物理研究所， 北京100029

摘要过套管电阻率测井是通过测量套管壁电势实现测量地层的视电阻率，基于传输线方程理论，针对层状地层，给出了套管壁电势、电流对地层横向电阻导数的微分方程(称Jacobi矩阵微分方程)及边界条件；利用Jacobi矩阵微分方程边值问题导出了过套管电阻率测井反演地层参数的Jacobi矩阵系数的解析表示, 利用Marquardt方法实现了过套管测井的地层电阻率反演；通过计算对Jacobi矩阵的特性进行了探讨，并获得了较快的计算速度(因为Jacobi矩阵是用解析解表示的),反演结果与地层模型取得了较好的逼近.本文实现了过套管电阻率测井地层参数的Jacobi系数矩阵的快速计算及地层电阻率反演，为进一步开展电阻率测井数据处理提供了理论依据和快速反演算法.关键词过套管电阻率测井； Jacobi矩阵； 传输线方法； 测井响应； 反演计算

1引言

过套管电阻率测井是油气井在开发过程中油气藏动态监测和剩余油地层重新评价的重要测井方法之一(Askey et al., 2002; Kaufman,1990; Kaufman and Wightman,1993; 尹军强等，1998；高杰等,2008; 刘福平等,2007; Vail, 1993; 谢树棋等,1999)，但自从20世纪30年代过套管电阻率测井被提出后的几十年间一直未取得突破性进展(Vail,1989,1991; Vail et al.,1993,1995; Schenkel and Morrision,1994,1990;Xie et al.,1999; 刘福平等,2013)．直到20世纪90年代初Kaufman发表了基于传输线方程的套管井电阻率测井近似理论模型和测量理论后(Benimeli et al., 2002; Kaufman,1990; Kaufman and Wightman,1993; 刘福平等,2013)，在过套管电阻率测井理论上和在测井仪器的研制上才取得了实质性进展(Aulia et al., 2001; Zhou et al.,2002；高杰等,2008; 刘福平等, 2007)．然而到目前为止，尚未涉及到过套管电阻率测井的参数反演问题.由于金属套管的电阻率与地层的电阻率存在巨大的差别(有的相差1010)，致使有限元、有限差分法离散方程的矩阵系数大小存在巨大差别，用这两种方法实现套管电阻率测井的正演计算仍然存在困难(目前还没见到成功的算例)，传输线方法已成为过套管电阻率测井成熟的正演计算方法(高杰等,2008; Fondyga et al.,2004；刘福平等,2013)，因此过套管电阻率测井参数反演的正演计算利用传输线方法目前应为一种好的选择(目前过套管电阻率测井的地层参数反演及Jacobi矩阵的计算尚未见到算法报道).要实现地层参数的反演关键是如何实现Jacobi矩阵的计算，反演计算时间的长短和精度取决于Jacobi矩阵的计算方法(魏宝君和张庚骥,2002; 丁继才等,2007; 张美根等，2003; 刑光龙等，2007；刘福平和杨长春,2003; Liu et al.,2012)，因此针对层状地层开展Jacobi矩阵算法研究具有重要意义.本文研究了套管壁电势、电流对地层横向电阻导数的Jacobi矩阵计算方法，导出了过套管电阻率测井反演地层参数Jacobi矩阵的解析表示，并探讨了Jacobi矩阵的特性，为进一步实现电阻率测井资料反演和测井数据解释都将具有实际意义.

2场分布的正演计算

设金属套管单位长度的电阻为Rc，金属套管单位长度所对应的地层的横向电阻为T(漏电电阻)，则传输线方程可写为(高杰等,2008; 刘福平等,2007)

(1)

(2)

(3)

其中

(4)

考虑n+1层地层后有

(5)

由于在n+1层中z可以取无限远，为保证电流I(z)有限，应取An+1=0， 设电源在坐标原点，则I1(0)=I0，其中I0为由电源流出而流向上半个空间的电流.利用电流源条件和方程(5)可得Bn+1、A1、B1，再利用公式(3)可得任意一层中的解.

3过套管电阻率测井的Jacobi矩阵

(6)

矩阵形式为

(7)

其中

(8)

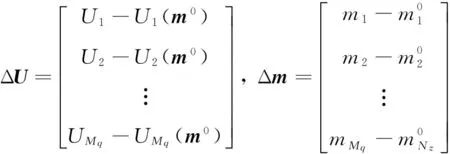
(9)

(8)式即为过套管电阻率测井观测数据对地层模型参数的导数(称Jacobi矩阵或敏感系数).

4Jacobi矩阵的计算方法

为了利用解析结果计算Jacobi矩阵，设观测数据也有Nz个(这样可以得到计算Jacobi矩阵的解析结果，利用这个解析解可以计算任意一个观测数据的Jacobi矩阵)，与网格个数相同.将方程(1)对Tj求导得第p层中电势、电流对Tj的导数方程

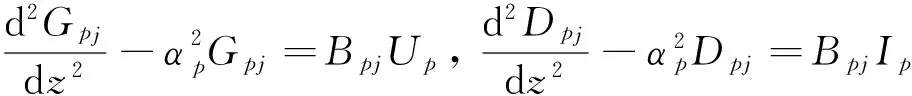
(10)

其中

(11)

在纵向多层状地层的界面电流、电势是连续的(方程同时对地层参数求导等式仍成立)，因此由于某一网格ΔTj的微小变化，在相邻两层中所引起的变化ΔU、ΔI(电荷守恒)也应该相等，所以Gpj、Dpj在地层界面是连续的(Zhangetal.,2003)，即Gp j(dp)=G(p+1)j(dp)，Dp j(dp)=D(p+1)j(dp).

(12)

(13)

(14)

(15)

由(13)(14)及(15)式得

(16)

实际上当观测数据少于网格个数时，因为p只是取整数，当p≠j时(第p、j层不在同一地层)，方程(10)为齐次方程，其通解为

(17)

由(13)式得

(18)

当p=j时(即第p、j层为同一地层)，观测点和方程(10)为非齐次方程，其特解

(19)

非齐次方程解为

(20)

同理

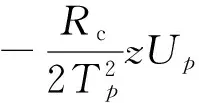
(21)

其中Ip、Up为方程(1)的解.若纵向有Nz层地层，利用Gpj、Dpj在地层界面连续可得两相邻地层均为齐次方程时的系数递推关系

(22)

其中

(23)

在方程(10)中每选一个j则有Nz个微分方程，只有当p=j时，微分方程为非齐次，在该层中由上界面连续边界条件(12)及(20)、(21)式得

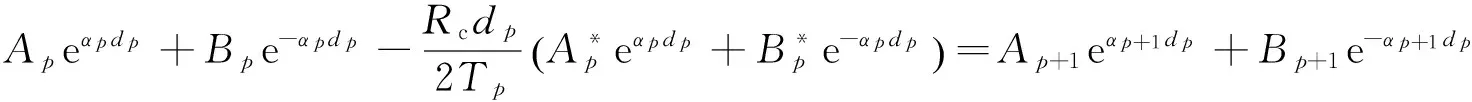
(24)

=Ap+1ηp+1eαp+1dp-Bp+1ηp+1e-αp+1dp,

(25)

写成矩阵形式有

(26)

其中

(27)

在第p层中由下界面连续边界条件(12)及(20)、(21)式得

(28)

(29)

由(22)式得

(30)

(31)

将(30)、(31)式代入(26)、(28)式得

(32)

由电流源(16)式得

(33)

在(32)、(33)式中只有A1、B1、An+1、Bn+1为未知常数，考虑到在z→∞时Gpj有限，则An+1=0，利用(32)、(33)式可计算A1、B1、Bn+1，再利用 (26)(28)及(22)式可确定全部待定系数，从而实现Jacobi矩阵的解析计算.

5过套管电阻率测井的地层电阻率反演方法

设反演目标函数为

(34)

其中Ud为过套管电阻率测井电势实际测量结果，U为地层模型电势响应(由地层模型计算的电势分布).设f(m)=U-Ud，则f(m)为地层模型电势响应与过套管电阻率测井电势实际测量结果所构成的参差函数，若设mk为m的第k次反演迭代近似.使反演目标函数极小得迭代公式

(35)

(36)

(37)

其中I为n阶单位矩阵，αk为一个正实常数，根据计算精度要求通过试算适当选取.

6数值算例及分析

6.1Jacobi矩阵特性分析

下面取四层状地层模型为算例，电极供电电流I0=6 A，电源位于坐标原点，套管电阻率为ρc=2.0×10-7Ωm, 套管半径a=0.1 m，套管厚度Δa=0.01 m,四层状地层界面位于dp=15,18,22 m，取观测数据点的坐标为z0=10,17,20,24 m(表1及图1均使用上述统一参数).表1的3种情况的差别仅是地层的电阻率不同，表的第2，3，4，5列分别为在z0=10,17,20,24 m测量点电势对第1，2，3，4层地层横向电阻的导数，表1中Case 1四层状地层的电阻率比较接近(ρb=1.1, 1.0,1.1,1.0 Ωm),表1中Case 3四层状地层的电阻率差距较大(ρb=20, 1,20,1 Ωm).表1显示地层电阻率对电势敏感系数(电势对地层横向电阻的导数)影响较大.图1为电势对地层横向电阻的导数随z坐标的变化曲线，由于金属套管的高导电性的影响(电势沿套管的变化缓慢，接近线性)，使得电势敏感系数随z坐标的变化基本呈线性关系，曲线1、2、3、4分别为测量点位置变化时(z坐标是变化的)，测量电势对第1，2，3，4层地层横向电阻的导数，图1中曲线1，2是重合的.在该算例中第4层是一个半无界的空间层，电势敏感系数与其他层的差别较大.

表1　电势对地层横向电阻的导数

cond(E)=2.372855356002384，4.141677504127008，3.873081055865031

6.2数值反演算例

为考察Jacobi矩阵的可靠性及反演方法的可行性,下面以三层状和五层状地层实现了过套管地层电阻率反演,除地层参数外,其余计算条件与前面图1算例相同.图2为三层状地层模型,其初值为15 Ωm,反演的最大相对误差为1.3%,反演结果与地层模型取得很好的逼近.图3为五层状地层模型, 其初值分为2段,第1,2层为8 Ωm,第3,4,5层为13 Ωm,反演结果见表2,其最大相对误差为2.2%,反演结果与地层模型也取得很好的逼近,验证了方法的可靠性与可行性.算例说明该方法是可以用于过套管电阻率的反演.

图1　电势对地层横向电阻的导数曲线Fig.1　Curves of derivations of potential with respect to transverse resistance of formation

地层序号12345模型参数Rs-mod/Ωm5.0010.0020.0010.0020.00反演初值Rs-st/Ωm8.008.0013.0013.0013.00反演结果Rs-inv/Ωm5.1110.2319.829.7819.79

7结论

本文针对层状地层，导出了过套管电阻率测井套管壁电势、电流对地层横向电阻导数(Jacobi系数矩阵)的解析表示，实现了地层参数反演中Jacobi系数矩阵的计算，选择Marquardt反演方法实现了过套管测井的地层电阻率反演.由于Jacobi系数矩阵计算的解析表示，可获得较快的计算速度.本文通过算例对Jacobi系数矩阵的特性进行了探讨，结果表明由于金属套管的高导电性影响使得电势敏感系数随z坐标的变化接近线性关系，且变化缓慢，地层电阻率的差异对电势敏感系数有较大影响；本算法是基于传输线方程实现的，同样克服了由于金属套管的电阻率与地层电阻率存在巨大差别给有限元、有限差分法模拟过金属套管问题所造成的困难.算例还考察了Jacobi矩阵特性，发现由Jacobi矩阵组成的反演方程属病态方程,针对反演迭代矩阵通过试验发现，利用每次反演迭代矩阵每行代数和的模作为Marquardt反演方法中每行的迭代校正因子,较好地改善了反演迭代系数矩阵条件数.本文提出了地层参数反演中Jacobi系数矩阵的计算方法及地层电阻率反演算法，并用解析的形式实现了Jacobi系数矩阵的计算，不仅计算精度高而且计算速度快(推导过程没有新的近似)，反演算例表明,反演结果能较好地逼近地层模型,为进一步的过套管电阻率测井数据处理提供了理论依据和方法.

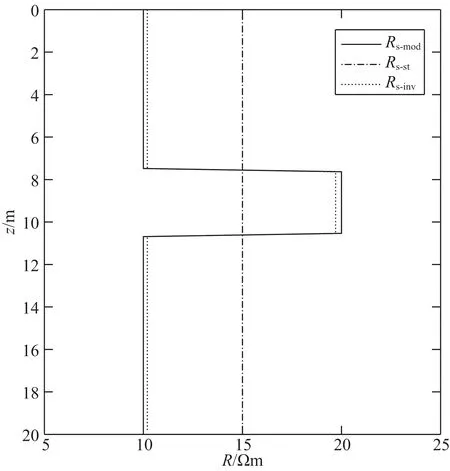
图2　地层电阻率反演结果(三层状地层)Fig.2　Inversion result of formation resistance (3-layer model)

图3　地层电阻率反演结果(五层状地层)Fig.3　Inversion result of formation resistance (5-layer model)

References

Askey S, Farag S, Logan J, et al. 2002. Cased Hole Resistivity Measurements Optimize Management of Mature Waterflood in Indonesia. ∥ SPWLA 43rd Annual Logging Symposium. Oiso, Japan: Society of Petrophysicists and Well-Log Analysts.

Aulia K, Poernomo B, Richmond W, et al. 2001. Resistivity behind casing.OilfieldReview, 13(1): 1-25.

Benimeli D, Levesque C, Rouault G, et al. 2002. A new technique for faster resistivity measurements in cased holes. ∥ SPWLA 43rd Annual Logging Symposium. Oiso, Japan: Society of Petrophysicists and Well-Log Analysts.

Ding J C, Chang X, Liu Y K, et al. 2007. Layer by layer waveform inversion of seismic reflection data.ChineseJ.Geophys. (in Chinese), 50(2): 574-580.

Fondyga A, Sherba G. 2004. Cased hole density, neutron, sonic and resistivity logging in South America, case histories, lessons learned, and a methodology for including the technology in formation evaluation programs.∥ SPWLA 45th Annual Logging Symposium. Noordwijk, Netherlands: Society of Petrophysicists and Well-Log Analysts.Gao J, Liu F P, Bao D Z, et al. 2008. Responses simulation of through-casing resistivity logging in heterogeneous-casing wells.ChineseJ.Geophys. (in Chinese), 51(4): 1255-1261.Kaufman A A. 1990. The electrical field in a borehole with a casing.Geophysics, 55(1): 29-38.

Kaufman A A, Wightman W E. 1993. A transmission-line model for electrical logging through casing.Geophysics, 58(12): 1739-1747.Liu F P, Yang C C. 2003. The numerical calculation of sensitivity coefficients of permeability field.ChineseJ.Geophys. (in Chinese), 46(1): 131-137.Liu F P, Gao J, Sun B D, et al. 2007. Forward calculation of the resistivity logging response through casing by transmission line equation for multi-layer formations.ChineseJ.Geophys. (in Chinese), 50(6): 1905-1913.Liu F P, Meng X J, Xiao J Q, et al. 2012. Applying accurate gradients of seismic wave reflection coefficients (SWRC) to the inversion of seismic wave velocities.ScienceChinaEarthSciences, 55(12): 1953-1960.

Liu F P, Chen X A, Zhao B C, et al. 2013. Instability analysis of through casing resistivity logging responses in higher resistance formation.WellLoggingTechnology(in Chinese), 37(1): 85-89.Schenkel C J, Morrision H F. 1994. Electrical resistivity measurement through metal casing.Geophysics, 59(7): 1072-1082.Schenkel C J, Morrision H F. 1990. Effects of well casing on potential field measurements using downhole current sources.GeophysicalProspecting, 38(6): 663-686.

Vail W B. 1989. Methods and apparatus for measurement of electronic properties of geological formations through borehole casing. U. S. Patent No. 4882542. November 21.

Vail W B. 1991. Methods and apparatus for measurement of the resistivity of geological formations from within cased well in presence of acoustic and magnetic energy sources. U. S. Patent No. 5043669. August 27.

Vail W B. 1993. Measuring resistivity changes from within a first cased well to monitor fluids injected into oil bearing geological formations from a second cased well while passing electrical current between the two cased wells. U. S. Patent No. 5187440. February 16.Vail W B, Momii S T, Woodhouse R, et al. 1993. Formation resistivity measurements through metal casing.∥ SPWLA 34th Annual Logging Symposium. Calgary, Alberta, Canada: Society of Petrophysicists and Well-Log Analysts.

Vail W B, Momii S T, Haines H, et al. 1995. Formation resistivity measurements through metal casing at the MWX-2 well in Rifle, Colorado.∥ SPWLA 36th Annual Logging Symposium. Paris, France: Society of Petrophysicists and Well-Log Analysts.Wei B J, Zhang G J. 2002. Forward modeling and inversion of 3-D cross-hole electromagnetic fields.ChineseJ.Geophys. (in Chinese), 45(5): 735-743. Xie S Q, Chu Z T, Li K P, et al. 1999. On methodology of resistivity logging through casing.WellLoggingTechnology(in Chinese), 23(5): 338-343.

Xing G L, Yang S D, Li S G. 2007. On the fast algorithm and characteristic analysis of Jacobi matrix in the inversion of electromagnetic wave logs.ChineseJ.Geophys. (in Chinese), 50(2): 642-650.

Yin J Q, Feng Q N, Zhu L D, et al. 1998. Feasibility study on formation resistivity measurement through metal casing.WellLoggingTechnology(in Chinese), 22(5): 376-379.

Zhang M G, Wang M Y, Li X F, et al. 2003. Full wavefield inversion of anisotropic elastic parameters in the time domain.ChineseJ.Geophys. (in Chinese), 46(1): 94-100.

Zhou Q, Julander D, Penley L. 2002. Experiences with casedhole resistivity logging for reservoir monitoring. ∥ SPWLA 43rd Annual Logging Symposium. Oiso, Japan: Society of Petrophysicists and Well-Log Analysts.

附中文参考文献

丁继才, 常旭, 刘伊克等. 2007. 反射地震数据的逐层波形反演. 地球物理学报, 50(2): 574-580.

高杰, 刘福平, 包德洲等. 2008. 非均匀套管井中的过套管电阻率测井响应. 地球物理学报, 51(4): 1255-1261.

刘福平, 杨长春. 2003. 渗透率场敏感系数的数值计算. 地球物理学报, 46(1): 131-137.

刘福平, 高杰, 孙宝佃等. 2007. 实际井眼条件下过套管电阻率测井响应的传输线方程正演算法. 地球物理学报, 50(6): 1905-1913.

刘福平, 陈小安, 赵宝成等. 2013. 过套管电阻率测井高电阻率层段不稳定性分析. 测井技术, 37(1): 85-89.

魏宝君, 张庚骥. 2002. 三维井间电磁场的正反演计算. 地球物理学报, 45(5): 735-743.

谢树棋, 储昭坦, 李克沛等. 1999. 套管井电阻率测井方法研究. 测井技术, 23(5): 338-343.

刑光龙, 杨善德, 李曙光. 2007. 电磁波测井资料反演中Jacobi矩阵的快速算法及其特性分析. 地球物理学报, 50(2): 642-650.

尹军强, 冯启宁, 朱龙德等. 1998. 通过金属套管测量地层电阻率的可行性研究. 测井技术, 22(5): 376-379.

张美根, 王妙月, 李小凡等. 2003. 时间域全波场各向异性弹性参数反演. 地球物理学报, 46(1): 94-100.

(本文编辑何燕)

基金项目北京市自然科学基金重点项目B类(KZ201510015015)；北京市自然科学基金(4142016)；北京市教委项目 (KM201510015009，KM201410015006，PXM2016_014223_000025)资助.

作者简介刘福平，男，1960年生，教授，1994年于石油大学勘探系获硕士学位，2002年于中国科学院地质与地球物理研究所获博士学位，2004年于中国科学院地质与地球物理研究所博士后出站，主要从事电磁波传播理论、数值计算及油藏数值模拟方面的研究和教学工作. E-mail: fupingliu@bigc.edu.cn, fupingliu60@sina.com.cn

doi:10.6038/cjg20160634 中图分类号P631

收稿日期2014-12-29，2015-12-05收修定稿

A fast inversion algorithm of formation resistivity for resistivity logging through casing

LIU Fu-Ping1,2， WANG An-Ling1， LIU Hua-Qun1， YANG Chang-Chun2

1BeijingInstituteofGraphicCommunication,Beijing102600,China2InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China

AbstractThe resistivity logging through casing is that the potential distribution on the metal casing is measured to realize the measurement of formation resistivity. For this method, this study derived the differential equations of Jacobi matrix from the transmission line equation and its boundary conditions for a multi-layered formation, which are the derivative equations of the potential and current with respect to the transverse resistance of formation. With the differential equations we have given the analytic formula of the Jacobi matrix and realized the inversion of formation resistivity (Marquardt inversion method). With computing examples, the characteristics of Jacobi matrix were discussed, and the fast computing speed was obtained, in which the results of inverse are in excellent agreement with the model of formation. The realization of formation resistivity inversion and its fast computation of Jacobi matrix provide a theoretical basis and a fast inversion algorithm for the further development of the resistivity logging and data processing.

KeywordsResistivity logging through casing; Jacobi matrix; Transmission line approach; Logging response; Inversion calculation

刘福平， 王安玲， 刘华群等. 2016. 过套管电阻率测井的地层电阻率快速反演算法. 地球物理学报，59(6):2326-2332,doi:10.6038/cjg20160634.

Liu F P, Wang A L, Liu H Q, et al. 2016. A fast inversion algorithm of formation resistivity for resistivity logging through casing.ChineseJ.Geophys. (in Chinese),59(6):2326-2332,doi:10.6038/cjg20160634.