基于GRACE KBRR数据的动力积分法反演时变重力场模型
2016-07-28罗志才周浩李琼钟波
罗志才, 周浩, 李琼, 钟波
1 武汉大学测绘学院, 武汉 430079 2 华中科技大学物理学院, 武汉 430074 3 华中科技大学地球物理研究所, 武汉 430074 4 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079
基于GRACE KBRR数据的动力积分法反演时变重力场模型
罗志才1,4, 周浩2,3*, 李琼2,3, 钟波1,4
1 武汉大学测绘学院, 武汉4300792 华中科技大学物理学院, 武汉4300743 华中科技大学地球物理研究所, 武汉4300744 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉430079
摘要基于动力积分法恢复了一组60阶的时变重力场模型WHU-Grace01s,且在位系数解算过程中仅使用KBRR数据.通过与CSR、GFZ和JPL发布的Release 05模型的阶方差和位系数误差谱对比可知,WHU-Grace01s模型在高阶次部分的阶方差较小,且对轨道共振现象不敏感.将WHU-Grace01s时变重力场模型与CSR、GFZ、JPL、DEOS、Tongji、ITG、AIUB和GRGS等8家机构发布模型通过相同的滤波处理,获得了全球地表质量变化的时空分布,从结果可以看出:各个模型计算的时变信号在空域上分布十分接近,且WHU-Grace01s模型计算的太平洋中心和撒哈拉沙漠区域的质量变化较小;对比几个典型质量变化区域,WHU-Grace01s模型和JPL模型计算的长江流域和珠江流域时变信号呈强相关,其相关系数分别为0.948和0.976,且与上述8个模型计算的两个流域时变信号的相关系数均达到0.9以上;在南极区域和格陵兰岛,WHU-Grace01s模型和其他各个模型均能反映区域冰川质量的积累或消融,且各模型计算获得的长期趋势变化结果相当.研究结果表明,WHU-Grace01s模型和国内外已发布机构模型具有很好的一致性,且受到轨道共振影响较小.
关键词时变重力场模型; GRACE; 动力积分法; 卫星重力
1引言
GRACE卫星任务的成功实施为人类了解地球内部构造及浅层物质运移开启了新纪元.自Wahr等(2004)发布第一组月重力场模型以来,基于GRACE卫星时变重力场模型的全球或局域陆地水储量变化研究(Chen et al.,2005a;Hu et al.,2006;Zhong et al.,2009;李琼等,2013;Feng and Zhong,2015)、极区冰盖质量变化研究(Luthcke et al.,2006a;Chen et al.,2008;Luo et al.,2012;Ju et al.,2014)等均取得了丰硕的研究成果,对地球物理学、大地测量学、海洋学和冰川学等领域的发展具有重要意义.
基于GRACE L1b数据获取时变重力场模型需要充分考虑各个载荷的误差特性和综合影响,且数据观测量大,时间跨度长,解算复杂.迄今为止,国际上仅有少数几家知名机构完成该项复杂工作,分别是德克萨斯大学空间研究中心(CSR,Center for Space Research)、美国宇航局喷气推进实验室(JPL,Jet Propulsion Laboratory)、德国地学研究中心(GFZ,GeoForschungsZentrum Potsdam)、波恩大学理论大地测量研究所(ITG,Institute of Theoretical Geodesy)、代尔夫特地球观测与空间系统研究所(DEOS,Delft institute of Earth Observation and Space system)、伯尔尼大学天文研究所(AIUB,Astronomical Institute, University of Bern)和法国空间研究中心空间大地测量研究所(GRGS,Groupe de Recherche de Geodesie Spatiale)等.国内的学者也长期致力于GRACE卫星任务恢复时变重力场模型,具有代表意义的有Shen等(2013)、冉将军等(2014)分别基于短弧法解算了时变重力场模型Tongji-GRACE01和IGG-CAS,且与国际知名机构发布模型的精度相当.表 1给出了国内外已发布时变重力场模型的统计信息,大部分机构选用动力积分法进行解算.在国内,周旭华(2005)、肖云(2006)、邹贤才(2007)、张兴福(2007)和王庆宾(2009)等在动力积分法恢复地球重力场静态信息方面做了大量研究.Zhao等(2011)联合轨道和KBRR观测数据,比较了经验参数的处理方式对时变重力场模型解算精度的影响.本文将在上述研究基础上编写一套动力积分法软件,以实现时变重力场模型反演.此外,Luthcke等(2006b)关于基线法的研究结果表明,由于轨道几何特性和共振周期等综合影响,仅使用KBRR(K-Band Range Rate)观测能够使某些特殊阶次的时变重力场模型精度更高.因此,本文仅采用KBRR观测值解算时变重力场模型.
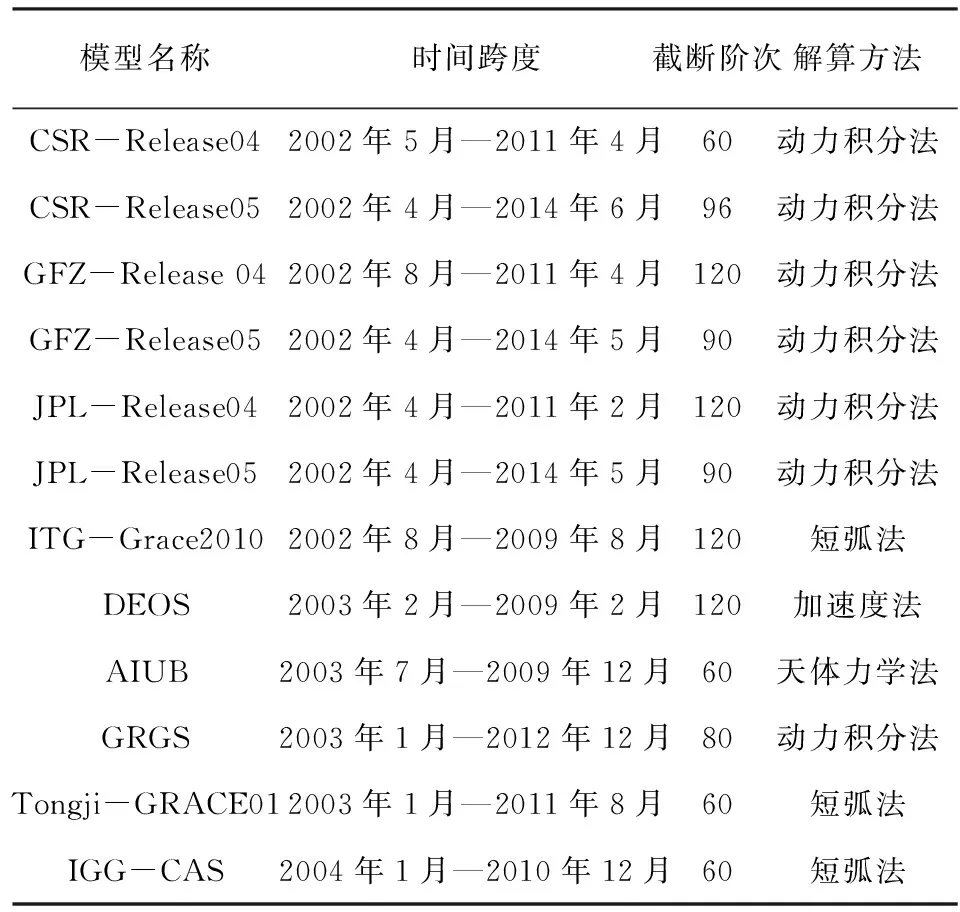
表1 已发布的时变重力场模型
2利用动力积分法反演时变重力场模型的基本原理
动力积分法是将卫星星历扰动作为地球重力场信息的泛函,通过建立轨道摄动与地球重力场位系数之间的关系,精密获取地球重力场模型的方法.
2.1基于HL-SST技术的动力积分法
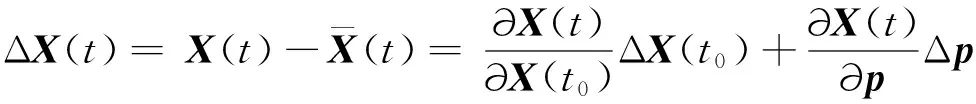
(1)
考虑到力模型误差的累积影响,动力积分法通常分弧段进行.待解算的未知数中,与弧段相关的变量称为局部变量,如整周模糊度和钟差等与GPS观测相关的变量、初始状态和加速度计校准参数等与轨道积分相关的变量;影响整个观测时段内的变量称为全局变量,这里主要指重力场位系数.根据对局部参数处理方式的不同,动力积分法可分为一步法、两步法和三步法.其中,一步法是基于公式(1)分弧段积分并构建法方程,然后通过法方程约化和叠加同时求解所有局部变量和全局变量;二步法首先利用载波和伪距完成定轨,然后将与轨道积分相关的局部变量和全局变量一并求解;三步法是依次求得局部变量,最后叠加弧段法方程求解全局变量.Luthcke等(2006b)采用三步法实现了基于KBRR观测解算时变重力场模型的基线法,取得了很好的计算结果.鉴于此,本文也将采用三步法实现动力积分法反演时变重力场模型.
精密校准星载加速度计是基于动力积分法获取高精度地球重力场模型的关键.本文引入加速度计三个观测方向的尺度因子k、偏差因子b.
(2)
其中,fobs为加速度计观测的非保守力,R为星固系转换至惯性系的旋转矩阵.在计算参数敏感矩阵时需要非保守力相对于校准因子的偏导数,依次表示为:
(3)
考虑到力模型误差对轨道积分的累积影响,通常在加速度计校准过程中引入尺度和偏差因子的先验参数,该参数可由地面数据处理中心获得(Bettadpur,2009).邹贤才(2007)的研究结果表明,静态重力场模型对基于参考模型的加速度计校准影响较大.因此,本文选用最新发布的纯GRACE重力场模型GGM05s为参考重力场模型.
2.2基于LL-SST技术的动力积分法



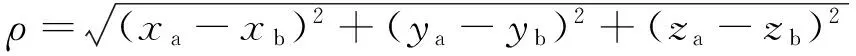
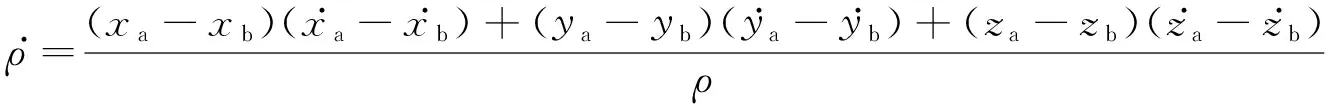
(4)
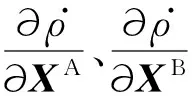
(5)
(6)

(7)
距s为:
(8)
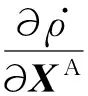
考虑到地球重力场同时作用于两颗卫星,根据偏导数计算的链式法则,星间距离变率对球谐系数c的偏导数可表示为:
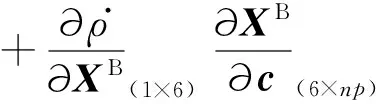
(9)
特别地,对于加速度计校准参数等与单个卫星飞行状态有关的力模型参数,距离变率对该类参数偏导数的计算方式与距离变率对初始状态的偏导数相一致;对于潮汐模型参数、三体引力参数等同时作用于两颗卫星的力模型参数,距离变率对该类参数偏导数的计算方式与距离变率对地球重力场位系数的偏导数相一致.
基于上述讨论,即可根据GRACE卫星LL-SST技术获取初始状态、加速度校准因子以及位系数等参数的最佳估值,获取精密动力学轨道,并更新地球重力场模型.需要注意的是,本文在更新地球重力场模型时,仅采用KBRR观测信息,未考虑轨道的影响.最后,利用各个月份观测数据解算重力场模型,减去平均重力场模型,即可获得各个月份的时变信息.
3基于GRACE L1b数据的时变重力场模型反演
本文利用动力积分法反演软件确定了GRACE时变重力场模型(周浩, 2015;Zhou et al.,2015),所有解算过程均采用联合OpenMP和MPI的并行函数库(周浩等,2011,2015),轨道积分和变分方程解算均采用Gauss-Jackson数值积分器(罗志才等,2013),力模型包括地球中心引力、非球形引力、三体摄动力、固体潮、海潮、大气潮、极潮、相对论效应、低阶次位系数的长周期变化和非保守力,非保守力由加速度计观测数据提供,地固系与惯性系的坐标旋转采用IERS2003协议,具体描述见表2.

表2 各项摄动力模型及其主要参数
本文计算均采用JPL提供的GRACE轨道数据、加速度计数据、星象仪数据和星间距离变率数据.考虑到观测数据存在空白和粗差等情况(郑伟等,2009),采用GRACE用户手册中提供的内插、重采样和剔除粗差的方法进行观测数据的预处理(Wu et al.,2006).以每个月的观测数据为一个单元,每24小时积分一个弧段,步长选为5 s,解算一组截断阶次为60的月重力场模型WHU-Grace01s.
4时变重力场模型分析
4.1模型解算精度
为了分析WHU模型(为表述方便,后文中均采用各个模型的发布机构代替相应的时变重力场模型名称)的解算精度,首先从2005年时变模型中减去全年的平均重力场信号,然后计算剩余时变信号的阶方差,与CSR、JPL、GFZ的Release05模型比较结果如图1所示.计算结果表明:第一,仅仅采用KBRR观测值解算的WHU模型在前20阶与其他三种模型的阶方差一致.第二,各个模型在2阶的阶误差RMS(Root Mean Square Error)差异较为明显,且WHU模型最小.Luthcke等(2006b)采用基线法的反演结果表明,仅使用KBRR观测值计算时变重力场模型的低阶次信号小于联合轨道和KBRR观测值的情况.第三,WHU模型在高阶次的阶方差逐步优于CSR、JPL和GFZ模型,全年的阶方差在60阶时均优于上述三个模型.Zhao等(2011)的研究结果表明,GRACE时变重力场模型的信号主要集中在前30阶次左右,随着阶次的增加,条带误差会淹没时变信号.由于没有引入轨道观测误差,仅采用KBRR观测值解算的WHU模型能够更好地抑制高频误差.

图1 WHU和CSR、JPL、GFZ的阶方差(2005年)Fig.1 Degree variance of CSR, JPL, GFZ and WHU (2005)

图2 WHU和CSR、JPL、GFZ的位系数误差谱(2005年9月)Fig.2 Coefficient error spectral of WHU, CSR, JPL and GFZ (September 2005)

图3 各种时变重力场模型计算的全球等效水高(2005年4月)Fig.3 Global EWH computed from different time-variable gravity field models (April 2005)
为了进一步分析模型解算精度,给出了2005年9月WHU和JPL、CSR、GFZ时变重力场模型的位系数误差谱,如图2所示.整体而言:由于GRACE卫星采用的南北飞行模式对带谐系数敏感,四种模型在带谐项误差小,扇谐项精度较差,且GFZ模型的误差最大.具体而言:在低阶次部分,WHU模型的位系数误差小于CSR、JPL和GFZ模型;在40阶次后,CSR、JPL和GFZ模型的相关误差较大,而WHU模型的相关误差也不如其他三个模型明显;特别地,由于仅采用KBRR观测数据,WHU模型在15、30、45阶等与轨道共振关系密切的阶次在位系数谱图中没有明显偏大的现象,而CSR、JPL和GFZ均有出现该现象.
4.2时变信号的空间分布
时变重力场模型可反映某个特定时间分辨率内全球或局部地表质量的变化特征,通常将时变重力场模型转换到空间域,利用等效水高(EWH,Equivalent Water Height)反映地表质量迁移的分布状况.由于观测误差以及先验地球物理场模型误差等综合影响,直接采用时变重力场模型计算的全球等效水高将会存在明显的南北向条带误差和高频误差(Swenson and Wahr,2006),而Gauss滤波、Fan滤波可有效削弱高频误差的影响(Wahr et al.,2004;Zhang et al.,2009),去相关滤波可以有效削弱南北向条带误差(Swenson and Wahr,2006).为了更加有效地削弱这部分影响,本文选用Fan滤波和去相关滤波的组合滤波方式(Luo et al.,2012),其中,Fan滤波半径取为500 km,去相关滤波选用P3M6.此外,由于对C2,0项不敏感,本文采用激光测卫数据解算的二阶项替代GRACE时变重力场模型中的C2,0项(Chen et al.,2005b).
将国内外9个机构发布的时变重力场模型转换到空间域,采用上述处理方式计算了2005年4月的全球等效水高变化,如图 3所示.与其他机构解算的时变重力场模型相比,WHU模型在全球大部分区域的时变信号分布趋于一致.结合Liu(2008)对流域的划分,各个模型计算的亚马逊流域的等效水高最大,处在雨季;非洲的刚果河和赞比西河等效水高均为正值;北美洲的密西西比河、马更些河流域,欧洲的多瑙河流域,俄罗斯境内的鄂毕河和叶尼塞河流域均为正值;北美洲的育空河流域,印度北部的恒河流域以及中国境内的珠江流域均为负值.
此外,选取了太平洋中心(146°W—134°W,17°S—23°S)和撒哈拉沙漠(10°E—20°E,20°N—30°N)等全年质量变化较小的区域,以评估时变重力场模型的反演精度.以2005年1月至2006年12月为例,计算上述两个区域在不加入任何滤波和加入组合滤波的EWH,截断阶次分别为20阶和60阶,最后给出了各个模型在该时间段内EWH的RMS(如表3所示).结果表明:滤波前,DEOS、WHU和GRGS模型的精度较高;滤波后,DEOS、Tongji、WHU和GRGS模型的精度较高.
4.3时变信号在特征流域的检核
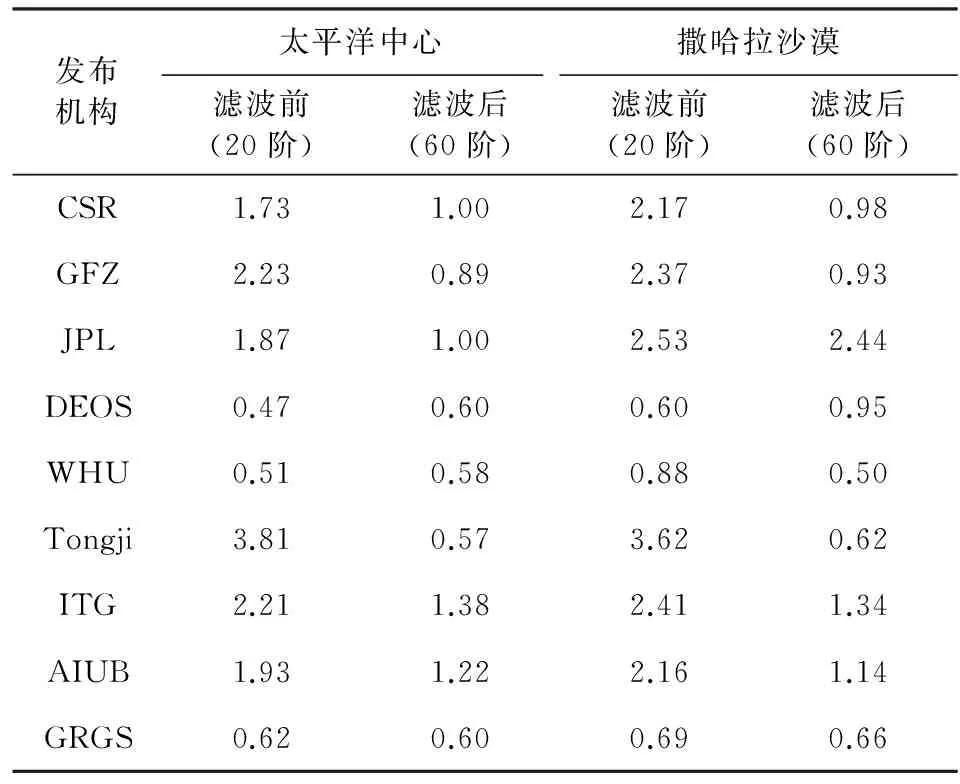
表3 各种时变重力场模型计算的EWH RMS(单位:cm)
为了更详细地分析WHU时变重力场模型与其他模型的一致性,计算了2003年1月至2008年12月的月重力场模型.以我国的长江流域和珠江流域为例,利用各个时变重力场模型分别计算了其水储量变化的时间序列(如图4和图 5所示),基于各时间序列得到了各个流域水储量变化的周年振幅A、周年相位φ和变化趋势P(如表 4所示),并比较了WHU模型与其他模型计算各个流域水储量变化的相关系数(如表5所示).其中,长江流域和珠江流域的相关系数平均值分别为0.900和0.949,WHU模型和JPL模型的相关系数最高,分别达到了0.948和0.976,且与CSR、GFZ、JPL、ITG、Tongji和GRGS在两个流域的相关系数均超过了0.90;以两个流域相关系数平均值为基准,WHU模型与各个机构模型的相关系数从大到小依次为JPL、Tongji、GRGS、CSR、ITG、GFZ、AIUB和DEOS.整体而言,WHU模型计算的流域水储量变化与其他模型的结果较为一致.
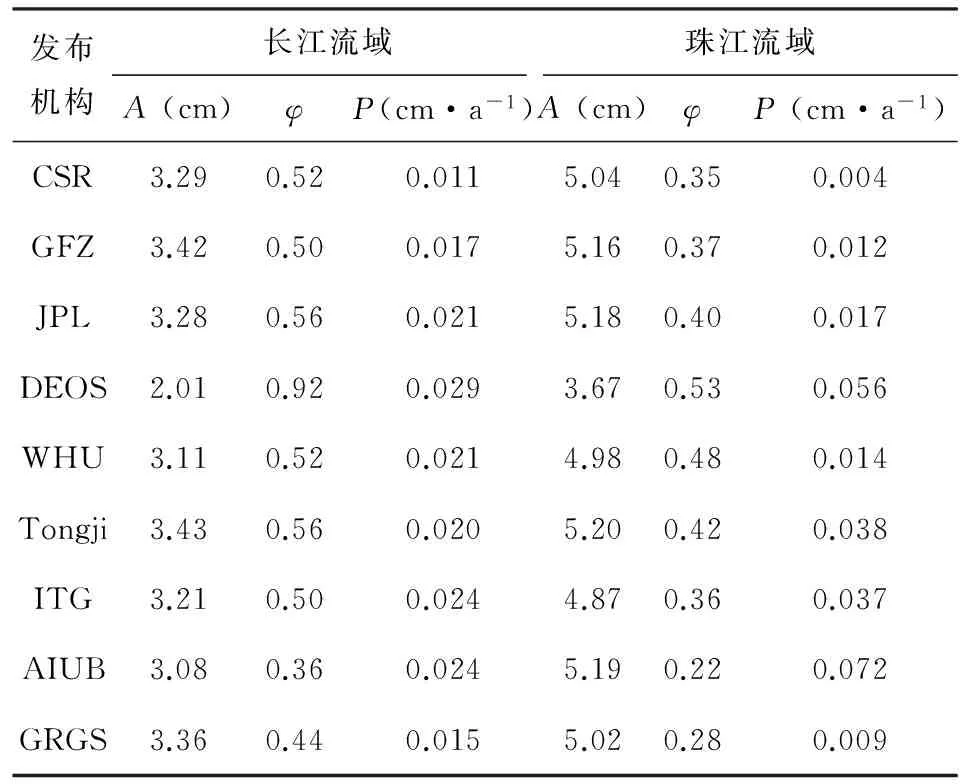
表4 各种时变重力场模型计算各个流域的统计信息

表5 WHU模型与其他模型计算各个流域水储量变化的相关系数

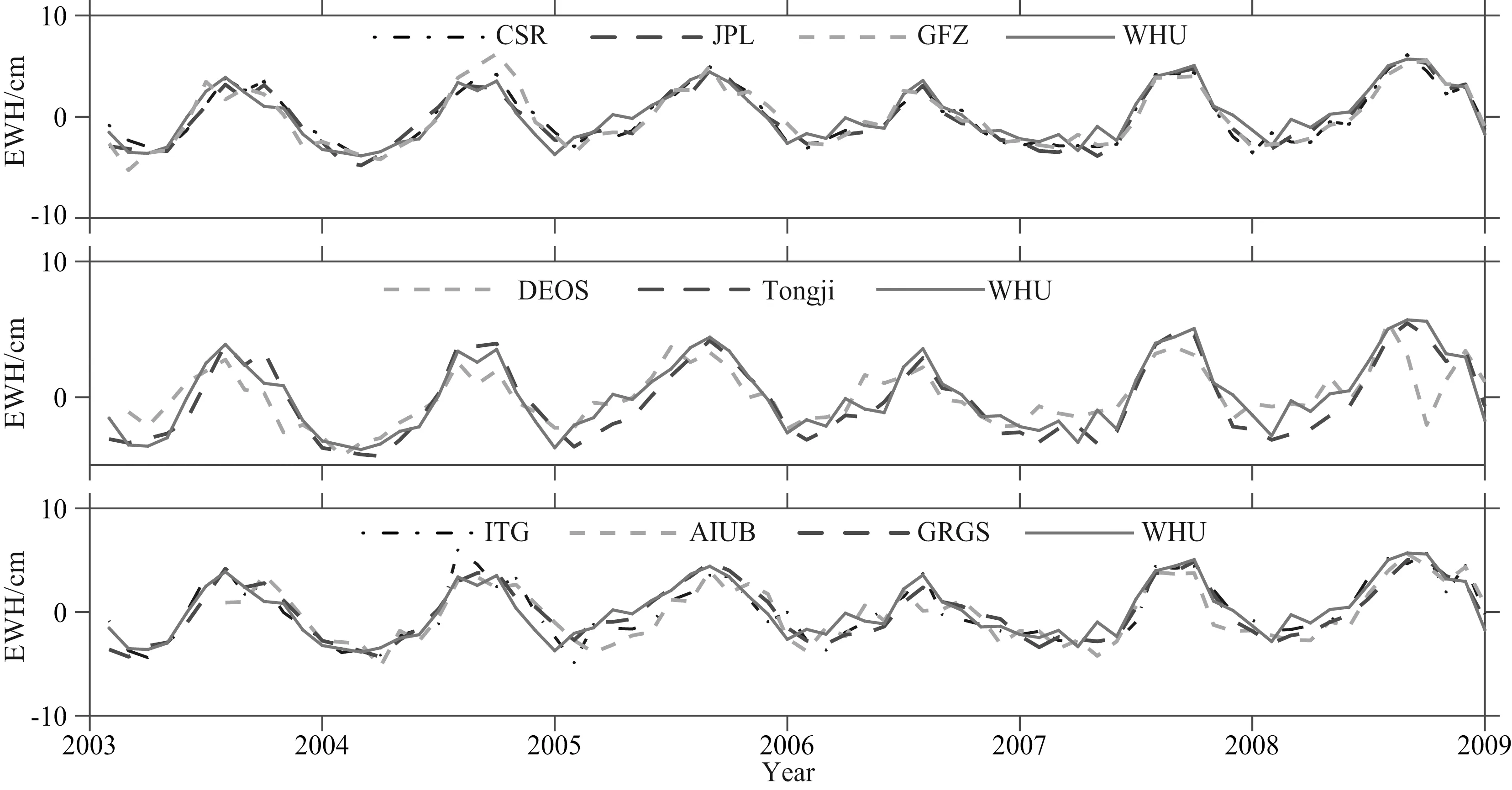
图4 各种时变重力场模型计算的EWH(长江流域)Fig.4 EWH of Yangtze river basin computed from different time-variable gravity field models

图5 各种时变重力场模型计算的EWH(珠江流域)Fig.5 EWH of Pearl river basin computed from different time-variable gravity field models
4.4时变信号在冰盖区域的检核
南极和格陵兰岛作为南北两极具有代表性意义的冰盖区域,是地球物理学、大地测量学、海洋学和冰川学等领域的热点研究区域,也是基于GRACE卫星探测全球质量变化的重要组成部分,因此,本文分别利用9个时变重力场模型计算了南极和格陵兰岛区域的地表质量变化率(如图6和图7所示).由于仅用于评价各个时变重力场模型,冰后回弹和泄露误差等对解算结果的影响是一致的,计算中并未考虑这些改正项.
对于南极区域,西南极Amundsen海湾(图6中A点)均表现为明显的质量减少趋势,是整个南极地区质量变化率最大的区域;B点Ronne冰架均表现为质量累积;C点北方为横贯南极的山脉,各个模型结果均表明该点附近的质量呈现增加趋势;各个模型在D点Wilkes Land的冰川呈现消融趋势,其中CSR和WHU模型的质量减少趋势最明显.
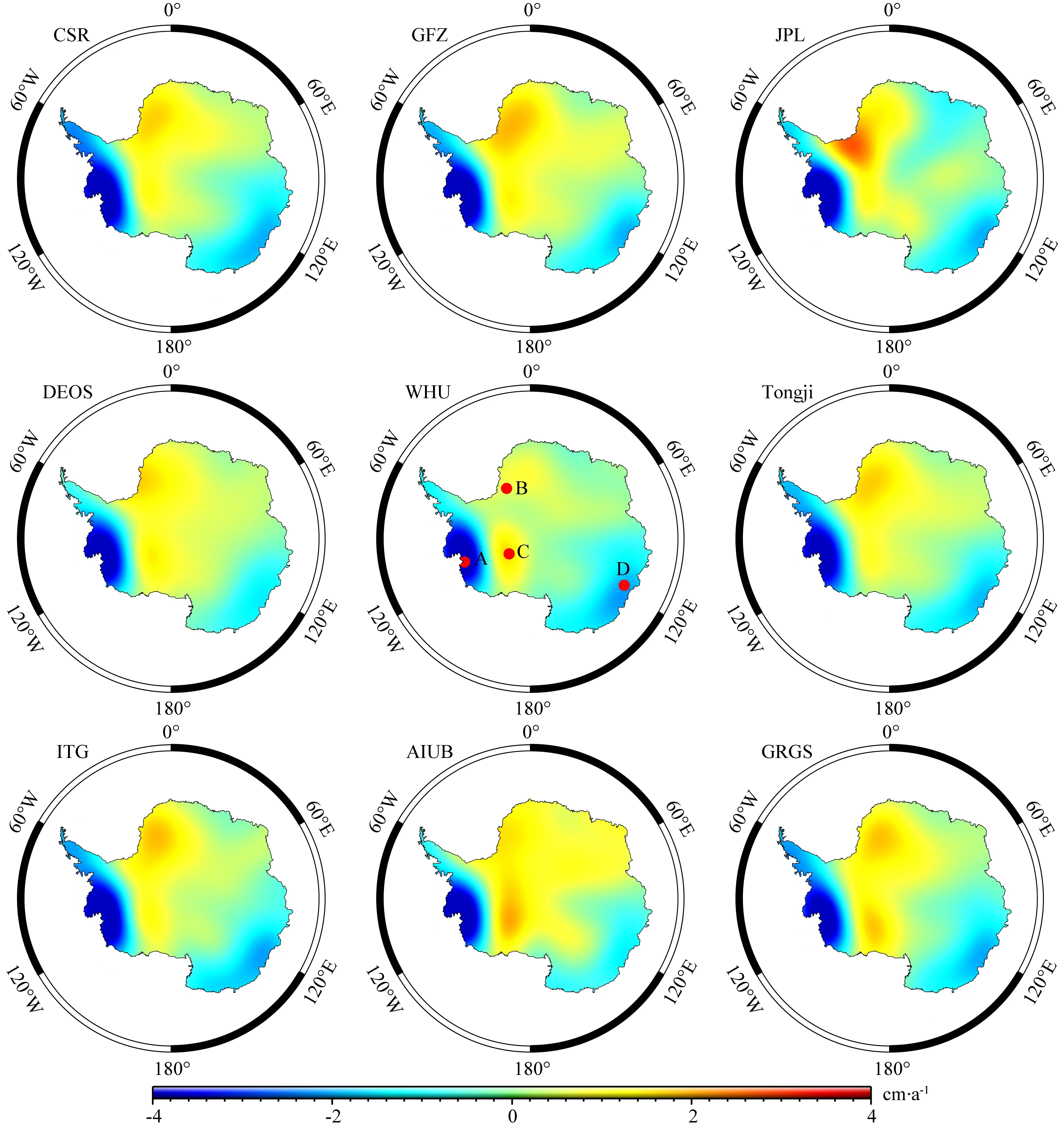
图6 各种重力场模型计算的南极地表质量变化率(2003年至2005年)Fig.6 The rate of Antarctic mass change recovered from released time-variable gravity field models (2003 to 2005)
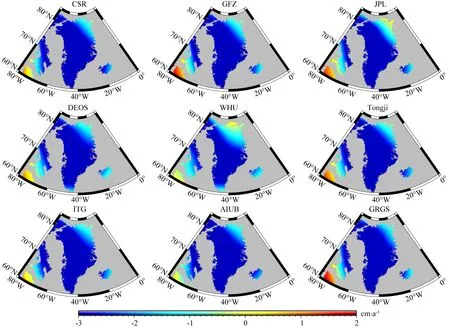
图7 各种时变重力场模型计算的格陵兰岛地表质量变化率(2003年至2005年)Fig.7 The rate of Greenland mass change recovered from released time-variable gravity field models (2003 to 2005)
对于格陵兰岛区域,各个模型计算的地表质量变化率表明,冰盖整体呈现消融的趋势,且中部和南部消融速度快,东北部的消融速度相对较小;格陵兰岛区域附近岛屿的地表质量变化率也趋于一致.特别的,WHU模型和JPL模型计算的格陵兰岛东北部有小部分出现质量增加现象,具体原因有待进一步查明.此外,利用CSR、GFZ、JPL、DEOS、WHU、Tongji、ITG、AIUB和GRGS等模型计算了2003年至2005年格陵兰岛冰盖质量年变化率,依次为-101 Gt/a、-98 Gt/a、-93 Gt/a、-81 Gt/a、-95 Gt/a、-91 Gt/a、-96 Gt/a、-95 Gt/a、-102 Gt/a,均与Luthcke 等(2006a)中采用Mascon解算结果-99 Gt/a相当.
5结论
本文实现了基于GRACE L1b数据反演时变重力场模型的动力积分法,仅采用KBRR观测数据解算了一组时间分辨率为1个月、截断阶次为60的时变重力场模型WHU-Grace01s,并通过多组数值计算比较了该模型与国内外知名机构发布模型的精度,得到如下结论:
(1) 通过与GFZ、JPL和CSR的Release 05模型对比可知,WHU模型在5至20阶次左右与上述三个模型的阶方差一致,而在高阶次部分的阶方差较小;相比于GFZ、JPL和CSR模型,WHU模型的位系数误差谱在15及其整数倍的阶次误差没有出现明显偏大的现象.
(2) 通过Fan滤波和去相关滤波的组合滤波处理后的全球等效水高表明,仅采用KBRR观测值解算的WHU模型在时变信号的空间分布上与其他模型相似,可明显探测大尺度范围的质量变化,且太平洋中心和撒哈拉沙漠等质量变化较小区域的精度较高.
(3) WHU模型与CSR、GFZ、JPL、DEOS、Tongji、ITG、AIUB和GRGS等8个模型计算的长江流域和珠江流域质量变化一致性较高,在上述两个流域的相关系数平均值分别可达0.900和0.949;WHU模型和JPL模型的相关系数最高,分别达到了0.948和0.976;与CSR、GFZ、JPL、ITG、Tongji和GRGS在两个流域的相关系数均超过了0.90.
(4) WHU模型与CSR、GFZ、JPL、DEOS、Tongji、ITG、AIUB和GRGS等8个模型计算的南极和格陵兰岛冰盖区域的质量变化率一致性较高.在南极,上述9个模型均能反映出Amundsen海湾、Ronne冰架、横贯南极山脉西南部部分区域、Wilkes Land等区域的质量增加或者减少;在格陵兰岛,上述9个模型计算的质量变化率依次为-91 Gt/a、-101 Gt/a、-98 Gt/a、-93 Gt/a、-81 Gt/a、-91 Gt/a、-96 Gt/a、-95 Gt/a、-102 Gt/a,均与Luthcke 等(2006a)仅使用KBRR观测数据解算的-99 Gt/a相当.
综上所述,本文解算的WHU-Grace01s模型与目前国内外主要机构发布的时变重力场模型精度相当.致谢感谢JPL提供解算所需的GRACE卫星观测数据,感谢两位匿名审稿专家对本文提出的宝贵修改意见.
References
Bettadpur S. 2009. Recommendation for a-priori bias and scale parameters for Level-1B ACC Data (Version 2). GRACE TN-02.
Chen J L, Wilson C R, Tapley B D, et al. 2005a. Seasonal global mean sea level change from satellite altimeter, GRACE, and geophysical models.J.Geodesy, 79(9): 532-539.
Chen J L, Rodell M, Wilson C R, et al. 2005b. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates.GeophysicalResearchLetters, 32(14): L14405.
Chen J L, Wilson C R, Tapley B D, et al. 2008. Antarctic regional ice loss rates from GRACE.EarthPlanet.Sci.Lett., 266(1-2): 140-148. Feng W, Zhong M. 2015. Global sea level variations from altimetry, GRACE and Argo data over 2005—2014.GeodesyandGeodynamics, 6(4): 274-279.
Hu X G, Chen J L, Zhou Y H, et al. 2006. Seasonal water storage change of the Yangtze River basin detected by GRACE.ScienceinChinaSeriesD, 49(5): 483-491.
Ju X L, Shen Y Z, Zhang Z Z. 2014. GRACE RL05-based ice mass changes in the typical regions of Antarctica from 2004 to 2012.GeodesyandGeodynamics, 5(4): 57-67.

Li Q, Luo Z C, Zhong B, et al. 2013. Terrestrial water storage changes of the 2010 southwest China drought detected by GRACE temporal gravity field.ChineseJ.Geophys. (in Chinese), 56(6): 1843-1849, doi: 10.6038/cjg20130606.Liu X L. 2008. Global gravity field recovery from satellite-to-satellite tracking data with the acceleration approach [Ph. D. thesis]. Delft: Delft University of Technology.
Luo Z C, Li Q, Zhang K, et al. 2012. Trend of mass change in the Antarctic ice sheet recovered from the GRACE temporal gravity field.ScienceChinaEarthSciences, 55(1): 76-82.
Luo Z C, Zhou H, Zhong B, et al. 2013. Analysis and validation of Gauss-Jackson integral algorithm.GeomaticsandInformationScienceofWuhanUniversity(in Chinese), 38(11): 1364-1368.
Luthcke S B, Zwally H J, Abdalati W, et al. 2006a. Recent Greenland ice mass loss by drainage system from satellite gravity observations.Science, 314(5803): 1286-1289.
Luthcke S B, Rowlands D D, Lemoine F G, et al. 2006b. Monthly spherical harmonic gravity field solutions determined from GRACE inter-satellite range-rate data alone.GeophysicalResearchLetters, 33(2): L02402.Ran J J, Xu H Z, Zhong M, et al. 2014. Global temporal gravity filed recovery using GRACE data.ChineseJ.Geophys. (in Chinese), 57(4): 1032-1040, doi: 10.6038/cjg20140402.Shen Y Z, Chen Q J, Xu H Z, et al. 2013. A modified short arc approach for recovering gravity field model. ∥GRACE Science Team Meeting. Austin, TX: Center for Space Research, University of Texas.Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data.GeophysicalResearchLetters, 33(8): L08402.
Wahr J, Swenson S, Zlotnicki V, et al. 2004. Time-variable gravity from GRACE: First results.GeophysicalResearchLetters, 31(11): L11501. Wang Q B. 2009. Study on the recovery of gravitational potential model with dynamical method [Ph. D. thesis](in Chinese). Zhengzhou: PLA Information Engineering University.
Wu S C, Kruizinga G, Bertiger W. 2006. Algorithm theoretical basis document for GRACE level-1B data processing V1. 2. Jet Propulsion Laboratory, California Institute of Technology.
Xiao Y. 2006. Research on the earth gravity field recovery from satellite-to-satellite tracking data [Ph. D. thesis] (in Chinese). Zhengzhou: PLA Information Engineering University.
Zhang X F. 2007. The earth′s field model recovery on the basis of satellite-to-satellite tracking missions [Ph. D. thesis] (in Chinese). Shanghai: Tongji University. Zhang Z Z, Chao B F, Lu Y, et al. 2009. An effective filtering for GRACE time-variable gravity: Fan filter.GeophysicalResearchLetters, 36(17): L17311.
Zhao Q L, Guo J, Hu Z G, et al. 2011. GRACE gravity field modeling with an investigation on correlation between nuisance parameters and gravity field coefficients.AdvancesinSpaceResearch, 47(10): 1833-1850.
Zheng W, Xu H Z, Zhong M, et al. 2009. Effective processing of measured data from GRACE key payloads and accurate determination of Earth′s gravitational field.ChineseJ.Geophys. (in Chinese), 52(8): 1966-1975, doi: 10.3969/j.issn.0001-5733.2009.08.003.
Zhong M, Duan J B, Xu H Z, et al. 2009. Trend of China land water storage redistribution at medi- and large-spatial scales in recent five years by satellite gravity observations.ChineseScienceBulletin, 54(5): 816-821.
Zhou H, Zhong B, Luo Z C, et al. 2011. Application of parallel algorithms based on OpenMP to satellite gravity field recovery.JournalofGeodesyandGeodynamics(in Chinese), 31(5): 123-127.
Zhou H. 2015. Study on the determination of the earth′s gravity field from the combination of multi-type satellite gravimetry data [Ph. D. thesis] (in Chinese). Wuhan: Wuhan University.
Zhou H, Luo Z C, Zhong B, et al. 2015. MPI parallel algorithm in satellite gravity field model inversion on the basis of least square method.ActaGeodaeticaetCartographicaSinica(in Chinese), 44(8): 833-839. Zhou H, Luo Z C, Zhong B. 2015. WHU-Grace01s: a new temporal gravity field model recovered from GRACE KBRR data alone.GeodesyandGeodynamics, 6(5): 316-323.
Zhou X H. 2005. Study on satellite gravity and its application [Ph. D. thesis] (in Chinese). Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences.
Zou X C. 2007. Theory of satellite orbit and earth gravity field determination [Ph. D. thesis] (in Chinese). Wuhan: Wuhan University.
附中文参考文献
李琼, 罗志才, 钟波等. 2013. 利用GRACE时变重力场探测2010
罗志才, 周浩, 钟波等. 2013. Gauss-Jackson积分器算法分析与验证. 武汉大学学报(信息科学版), 38(11): 1364-1368.
冉将军, 许厚泽, 钟敏等. 2014. 利用GRACE重力卫星观测数据反演全球时变地球重力场模型. 地球物理学报, 57(4): 1032-1040, doi: 10.6038/cjg20140402.
王庆宾. 2009. 动力法反演地球重力场模型研究[博士论文]. 郑州: 中国人民解放军信息工程大学.
肖云. 2006. 基于卫星跟踪卫星数据恢复地球重力场的研究[博士论文]. 郑州: 中国人民解放军信息工程大学.
张兴福. 2007. 应用低轨卫星跟踪数据反演地球重力场模型[博士论文]. 上海: 同济大学.
郑伟, 许厚泽, 钟敏等. 2009. GRACE卫星关键载荷实测数据的有效处理和地球重力场的精确解算. 地球物理学报, 52(8): 1966-1975, doi: 10.3969/j.issn.0001-5733.2009.08.003.
周浩, 钟波, 罗志才等. 2011. OpenMP并行算法在卫星重力场模型反演中的应用. 大地测量与地球动力学, 31(5): 123-127.
周浩. 2015. 联合多类卫星重力数据反演地球重力场的研究[博士论文]. 武汉: 武汉大学.
周浩, 罗志才, 钟波等. 2015. 利用最小二乘直接法反演卫星重力场模型的MPI并行算法. 测绘学报, 44(8): 833-839.
周旭华. 2005. 卫星重力及其应用研究[博士论文]. 武汉: 中国科学院测量与地球物理研究所.
邹贤才. 2007. 卫星轨道理论与地球重力场模型的确定[博士论文]. 武汉: 武汉大学.
(本文编辑何燕)
基金项目国家自然科学基金项目(41131067,41374023,41474019,41504014,41504015);大地测量与地球动力学国家重点实验室开放基金项目(SKLGED2015-1-3-E);中国博士后科学基金项目(2016M592337)资助.
作者简介罗志才,男,1966年生,工学博士,教授,博士生导师,现主要从事物理大地测量学和卫星重力学研究.E-mail:zhcluo@sgg.whu.edu.cn*通讯作者周浩,男,1987年生,工学博士,主要从事卫星重力数据处理及应用研究.E-mail:lengyeshanren@126.com
doi:10.6038/cjg20160606 中图分类号P223 年中国西南干旱陆地水储量变化. 地球物理学报, 56(6):1843-1849, 10.6038/cjg20130606.
收稿日期2015-01-27,2015-06-15收修定稿
A new time-variable gravity field model recovered by dynamicintegral approach on the basis of GRACE KBRR data alone
LUO Zhi-Cai1,4, ZHOU Hao2,3*, LI Qiong2,3, ZHONG Bo1,4
1SchoolofGeodesyandGeomatics,WuhanUniversity,Wuhan430079,China2SchoolofPhysics,HuazhongUniversityofScienceandTechnology,Wuhan430074,China3InstituteofGeophysics,HuazhongUniversityofScienceandTechnology,Wuhan430074,China4KeyLaboratoryofGeospaceEnvironmentandGeodesy,MinistryofEducation,WuhanUniversity,Wuhan430079,China
AbstractA new monthly time-variable gravity field model WHU-Grace01s truncated to 60 degrees and orders is determined solely from GRACE KBRR data using dynamic integral approach in this paper. Compared with the Release 05 models from CSR, GFZ and JPL, the degree variance of WHU-Grace01s are smaller in high degrees, and it is not very sensitive to orbit resonance phenomenon. After applying the same filter to the temporal signals derived from the time-variable gravity field models published by WHU, CSR, GFZ, JPL, DEOS, Tongji, ITG, AIUB and GRGS, we can get several useful conclusions as follows, the distribution of temporal signal computed by WHU-Grace01s is similar to the other models, and its signal in the Pacific Ocean center and Sahara desert is relative smaller. The correlation coefficients of the temporal signal in Yangtze river and Pearl river basin between WHU-Grace01s and JPL can reach to 0.948 and 0.976 respectively, the average correlations coefficients between WHU-Grace01s and the aforementioned 8 time-variable gravity field models is bigger than 0.90. All of the aforementioned time-variable gravity field models can detect the mass loss or accumulation in the Antarctica and Greenland, and the mass loss rate is similar to each other. In short, the accuracy of WHU-Grace01s has a good consistency with the previously published GRACE solutions, while the impact of orbit resonance on WHU-Grace01s is unconspicuous.
KeywordsTime-variable gravity field model; GRACE; Dynamic integral approach; Satellite gravity
罗志才, 周浩, 李琼等. 2016. 基于GRACE KBRR数据的动力积分法反演时变重力场模型.地球物理学报,59(6):1994-2005,doi:10.6038/cjg20160606.
Luo Z C, Zhou H, Li Q, et al. 2016. A new time-variable gravity field model recovered by dynamic integral approach on the basis of GRACE KBRR data alone.ChineseJ.Geophys. (in Chinese),59(6):1994-2005,doi:10.6038/cjg20160606.
