陕西省地形起伏度最佳计算单元研究

陈学兄, 张小军, 常庆瑞

(1.山西农业大学 资源环境学院, 山西 太谷 030801; 2.山西农业大学 园艺学院,山西 太谷 030801; 3.西北农林科技大学 资源环境学院, 陕西 杨凌 712100)



陕西省地形起伏度最佳计算单元研究

陈学兄1, 张小军2, 常庆瑞3

(1.山西农业大学 资源环境学院, 山西 太谷 030801; 2.山西农业大学 园艺学院,山西 太谷 030801; 3.西北农林科技大学 资源环境学院, 陕西 杨凌 712100)

摘要：[目的] 确定陕西省地形起伏度最佳计算单元,分析地形起伏度的空间分布规律,为地貌类型划分提供基础数据。[方法] 以陕西省90 m×90 m的航天飞机雷达地形测绘使命(SRTM)数字高程模型(DEM)数据为基础,首先利用邻域统计分析法〔矩形邻域选取2×2,3×3,4×4,…,35×35共34个不同大小的邻域窗口,圆形邻域窗口选取20个(邻域半径R为2～21)〕对陕西省地形起伏度进行提取,然后统计不同矩形窗口和圆形窗口下的各种地形起伏度类型所占面积比例,接着运用均值变点分析法计算最佳计算单元,最后完成陕西省地形起伏度分级图的绘制,并对地形起伏度特征进行分析。[结果] 不同地形起伏度类型所占面积比例的变化各有不同。按矩形邻域计算的地形起伏度最佳计算单元为12×12,对应面积为898 704 m2,按圆形邻域计算的地形起伏度最佳计算单元为R=8,对应面积为1 254 191.4 m2,这说明在使用邻域分析法提取地形起伏度时,采用圆形邻域有别于采用矩形邻域。陕西省地形总体较平缓,主要以小起伏、中起伏为主。[结论] 简单实用的均值变点分析法,是确定最佳计算单元的一种较为理想的方法。

关键词：土壤侵蚀; 航天飞机雷达地形测绘使命; 数字高程模型; 地形起伏度; 最佳计算单元; 陕西省

文献参数： 陈学兄, 张小军, 常庆瑞.陕西省地形起伏度最佳计算单元研究[J].水土保持通报，2016,36(3)：265-270.DOI:10.13961/j.cnki.stbctb.2016.03.046

水土流失是土地退化的主要原因，也是生态环境恶化的重要因素[1]。陕西省是中国水土流失、沙化等环境问题最严重的地区之一，水土流失面积占全省土地总面积的66.9%，是制约区域经济发展的重要因素[2]。水土流失发生和发展的潜在条件主要有气候、土壤、地形、地质、植被等。地形对水土流失的影响包括坡度、坡长、坡向、坡形及地形起伏度等因素的影响[3]，其中地形起伏度又是区域水土流失评价的地形指标[4]。为此，选用适用于区域尺度的90 m×90 m SRTM DEM数据，对陕西地形起伏度进行准确地提取，是开展水土流失定量评价的基础性工作。

地形起伏度(relief amplitude)是指在某一个确定面积内最大高程与最小高程之差[5]。它是定量描述地貌形态、划分地貌类型的重要指标，是描述一个区域地形特征的宏观性指标，它反映地面的起伏状况和切割程度。近年来，地形起伏度被广泛应用于土壤侵蚀敏感性评价、区域滑坡灾害评价、水土流失定量评价、地质环境质量评价等方面[4,6-9]。利用数字高程模型(digital elevation model, DEM)为基本数据进行地形起伏度的提取与分析，是获取所需地表信息的快速有效手段[5]。目前，利用DEM对地形起伏度的提取已有一些研究成果[4,10-15]，已有研究发现不同地区、不同地貌类型对应不同的地形起伏度最佳分析区域。鉴于此，本研究利用邻域分析法对陕西省地形起伏度因子进行了提取，为避免主观因素的影响，选用均值变点分析法确定陕西省地形起伏度的最佳计算单元，并对其地形起伏度特征进行了分析，以期为地貌类型划分提供基础数据，也为地形起伏度的进一步研究和应用提供参考。

1研究区概况

陕西省地处中国西北地区(105°29′—111°15′E，31°42′—39°35′N)，东邻山西、河南省，西连宁夏、甘肃省，南抵四川、重庆、湖北省，北接内蒙古，居于连接中国东、中部地区和西北、西南的重要位置。陕西省地域狭长，地势南北高，中间低，有高原、山地、平原和盆地等多种地形，全省总面积为2.058×105km2。研究区横跨3个气候带，南北气候差异较大。陕南属北亚热带气候，关中及陕北大部属暖温带气候，陕北北部长城沿线属中温带气候。年平均降水量340～1 240 mm，降水南多北少，陕南为湿润区，关中为半湿润区，陕北为半干旱区。

2材料与方法

2.1数据来源与处理

本研究的基础数据为:全国数字高程模型(SRTM DEM,90 m分辨率),数据采样格网大小为79 m,其数据格式为ArcGIS的Grid格式,地理坐标系为:WGS_1984_Albers;陕西省矢量边界图,其地理坐标系与SRTM DEM数据相同,利用该矢量边界图从全国DEM栅格数据上截取出陕西省范围的DEM数据。

2.2研究方法

2.2.1邻域分析法地形起伏度的提取利用邻域分析法进行。邻域统计计算过程中的分析窗口有矩形、圆形、环形和扇形共4种[16]。本文选取矩形窗口和圆形窗口，矩形窗口大小为n×n像元(n=2,3,4,…,35)，圆形窗口的邻域半径R为2～21。计算过程为(以矩形窗口为例)：首先统计n×n窗口内像元的最大值(max)与最小值(min)；然后计算出最大值与最小值的差值，该差值即为n×n窗口的地形起伏度值；接着用n×n窗口的地形起伏度栅格数据统计各窗口下的平均起伏度值(表1)。利用同样的计算步骤对圆形邻域窗口下的陕西省地形起伏度进行计算，结果见表2。

2.2.2确定最佳计算单元地形起伏度研究的关键是确定最佳计算单元[5]，即得出一确定面积，能恰到好处地反映地貌体的完整性，并具有一定范围内较强的代表性，即普适性。目前，国内关于这方面的研究也越来越受到关注，且取得了一些研究成果[4,10-15]，如刘新华等[4]利用1∶100万DEM数据分析中国水土流失地形因子时，确定的地形起伏度的最佳计算单元为5 km×5 km；高守英等[10]利用1∶1万的DEM数据分析龙口市泳汶河流域的地貌形态时，使用的最佳计算单元为2.5 km×2.5 km；唐飞等[11]利用1∶25万的DEM数据提取新疆克拉玛依地区地形起伏度时，得出准格尔盆地及其西北山区地形起伏度计算的最佳单元为20×20的网格大小(即4 km2)；王玲等[12]利用1∶25万DEM数据计算得出8×8的网格大小(2.56 km2)为新疆地形起伏度计算的最佳单元，并绘制了新疆地形起伏度分级图；王岩等[13]利用贵德地区1∶5万地形图等高线数据，分析得到该区地形起伏度计算的最佳单元为400 m×400 m，并制作了地形起伏度专题图；曹伟超等[14]利用ASTER GDEM数据，得到了整个西南地区19种地貌类型的分布图，同时得出2.34 km2为西南地区地形起伏度计算的最佳单元；郎玲玲等[15]基于1∶25万和1∶10万的DEM分析了福建省地形起伏度最佳计算单元的大小，得出对于福建地区1∶25万DEM下，4.41 km2为最佳计算单元，而1∶10万DEM下，0.4 km2为最佳计算单元。可见不同地区、不同分辨率DEM、不同DEM数据类型，所使用的最佳计算单元大小是有区别的。

3结果与分析

3.1邻域面积与地形起伏度关系分析

对不同矩形邻域所对应的面积进行了计算，结果见表1。从表1可知，最大起伏度起初随着邻域面积的增大而迅速增大，但当达到一定的阀值时其增大的趋势逐渐平缓，变化幅度不是很稳定，而平均起伏度在邻域面积达到一定大小时，其变化幅度是很平稳的；同样对不同圆形邻域所对应的面积进行了计算，结果见表2。圆形邻域窗口下的最大起伏度及平均起伏度的变化趋势与矩形邻域窗口下的比较相似。

表1　矩形邻域面积与地形起伏度关系

表2　圆形邻域面积与地形起伏度关系

3.2各种类型地形起伏度变化分析

根据中国1∶100万数字地貌制作规范[17]可对地形起伏度做如下划分：平原(≤30 m)、台地(30～70 m)、丘陵(70～200 m)、小起伏山地(200～500 m)、中起伏山地(500～1 000 m)、大起伏山地(1 000～2 500 m)、极大起伏山地(>2 500 m)。因研究区域地形起伏度均小于2 500 m，所以地形起伏度可划分为平原、台地、丘陵、小起伏山地、中起伏山地及大起伏山地6种类型。按此划分标准对陕西省不同矩形窗口和圆形窗口下的地形起伏度进行分级，统计每种地形起伏度类型的面积，并绘制每种地形起伏度类型所占面积百分比随邻域窗口增大的变化曲线图(如图1所示)。

从图1a可以看出，每个级别所占面积比例的变化各有不同。其中，地形起伏度小于30 m的平原地区、30～70 m之间的台地，其所占面积比例随邻域窗口增大呈逐渐减少的趋势；70～200 m之间的丘陵地区，所占面积比例随邻域窗口增大呈先增后减的趋势，邻域窗口为5×5时，丘陵所占面积比例达到峰值，占全区面积的56.44%；对于200～500 m之间的小起伏山地，所占面积比起初随邻域窗口增大而迅速增大，但当邻域窗口为12×12时，增加趋势很平缓，增幅很小；对于500～1 000 m之间的中起伏山地，起初所占面积极少，当邻域窗口达到8×8之后，随邻域窗口增大呈明显上升趋势；对于地形起伏度大于1 000 m的大起伏山地，起初所占面积为0，当邻域窗口达到22×22之后，随邻域窗口增大呈现缓慢增加的趋势。

由图1b得知，矩形邻域和圆形邻域两种情况下各种地形起伏度所占面积比例的变化趋势大致相同，但也略有差异。地形起伏度介于70～200 m之间的丘陵地区，所占面积比例的最高值出现在邻域面积为0.176 4 km2(R=3)对应的位置上，较矩形邻域对应的0.156 0 km2大，所占面积比例为55.92%；地形起伏度在200～500 m之间的小起伏山地，所占面积比例在邻域面积为0.960 24 km2(R=7)时，其增加趋势开始平缓的，比矩形邻域下的0.898 7 km2(12×12)大，所占面积比例为36.65%；地形起伏度在500～1 000 m之间的中起伏山地，起初所占面积也为0，当R=4时，随邻域窗口增大呈明显上升趋势，所对应的邻域面积为0.313 55 km2，较矩形邻域下的0.399 424 km2(8×8) 小；圆形邻域下在对应面积为3.311 849 km2(R=13)的位置出现地形起伏度大于1 000 m的情况，而在矩形邻域下这个面积为3.020 64 km2(22×22)。上述结果表明，使用邻域窗口分析法提取地形起伏度时，圆形邻域有别于矩形邻域。

图1　地形起伏度类型面积百分比的变化曲线

3.3确定最佳尺度地形起伏度

3.3.1最佳计算单元确定原则地形起伏度最佳计算单元需要满足山体完整性和区域普适性原则[5]。山体完整性原则，即统计区域需能恰当地反映山体的完整性。以山体上的任一点为邻域中心，随着邻域范围的增加，会将更大和更小的山体包括进来，使区域内高程极值范围发生改变，目标栅格点起伏度也随着发生变化。这个高差值一般随着分析窗口的增大而增大，当范围增加到把整个山体都包括时，高差值的增幅变得较小，将地形起伏度增加幅度由大变小的尺度定义为变点，变点所对应的尺度即为最佳计算单元，这一尺度下的地形起伏度，恰到好处地反映了山体的起伏状况，要提取适合一个地区的计算单元，需将满足最大山体山体完整性的计算单元求出，此计算单元一定会满足较小山体的山体完整性原则，从而达到区域普适性的要求。

3.3.2确定最佳计算单元确定一个合适的分析区域或分析窗口半径，使得在宏观范围内的起伏度能够准确地反映地面的起伏状况，是地形起伏度提取中的核心步骤和决定区域起伏度信息提取效果与有效性的关键[15]。起伏度随邻域面积的变化曲线呈逻辑斯蒂克曲线[12]，最佳计算单元的大小确定即在该曲线由陡变缓处。利用Excel软件的统计功能对表1中的邻域面积与平均起伏度及表2中的邻域面积与平均起伏度分别进行对数方程拟合，得出拟合曲线(图2)。图2中x轴为邻域面积；y轴为平均起伏度。由图2可见，矩形邻域窗口下的平均起伏度与邻域面积的拟合曲线为y=62.002 ln(x)-64.032，决定系数R2=0.982 9，而圆形邻域窗口下的平均起伏度与邻域面积的拟合曲线为y=64.586 ln(x)-79.747，决定系数R2=0.986 4，拟合效果要比矩形邻域的好一些。

一般依靠目视判断来确定拟合曲线上由陡变缓的这一点，但目视判断易受主观因素的影响，所以本研究选用统计学上的均值变点分析法来计算所拟合的曲线上由陡变缓的这一点，均值变点分析法对恰有1个变点的检验最为有效，已被国内学者用于计算地形起伏度最佳单元[12]。所谓的变点是指模型或输出序列在某未知时刻起了突然变化，该时刻即为系统的变点，均值变点分析的目的是判断和检验变点的存在位置，并估计出变化的跃度[12]。

图2　邻域面积与平均地形起伏度对应关系拟合

在使用均值变点分析法计算变点之前，先要对表1—2中的数据分别进行一些处理，以构建一个样本序列，在此以表1数据为例说明其计算过程：

(1) 利用公式(1)计算各个分析窗口下单位面积上的地势大小序列T(单位地势度)：

Ti=ti/si(i=2，3，4，…，35)

(1)

式中:Ti——分析窗口下的单位地势度;ti——分析窗口下的平均起伏度;si——分析窗口的邻域面积(m2);i——矩形邻域的边长(m)。

(2) 对序列T取对数ln(T),得序列X,X为{xi，i=1，2，3，…，34}。

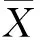
(2)

(3)

(4)

表3　均值变点分析的统计结果

利用统计软件做出S与Si差值的变化曲线(图3)。由图3可看出矩形邻域分析法在第11个点时S与Si的差值达到了最大，而圆形邻域分析法在第7点时S与Si的差值最大，这一点就是所要求的点。

由此得出，基于90 m×90 m SRTM DEM数据的陕西省地形起伏度最佳计算单元大小为12×12和R=8两个尺度。

3.4地形起伏度特征分析

附图12为最佳计算单元(12×12和R=8)地形起伏度分级图，从分级图可清晰的看出陕西地区地形起伏的分布格局。

统计两种邻域计算方法得出的最佳尺度地形起伏度各种类型所对应的像元数及面积百分比(如表4所示)。

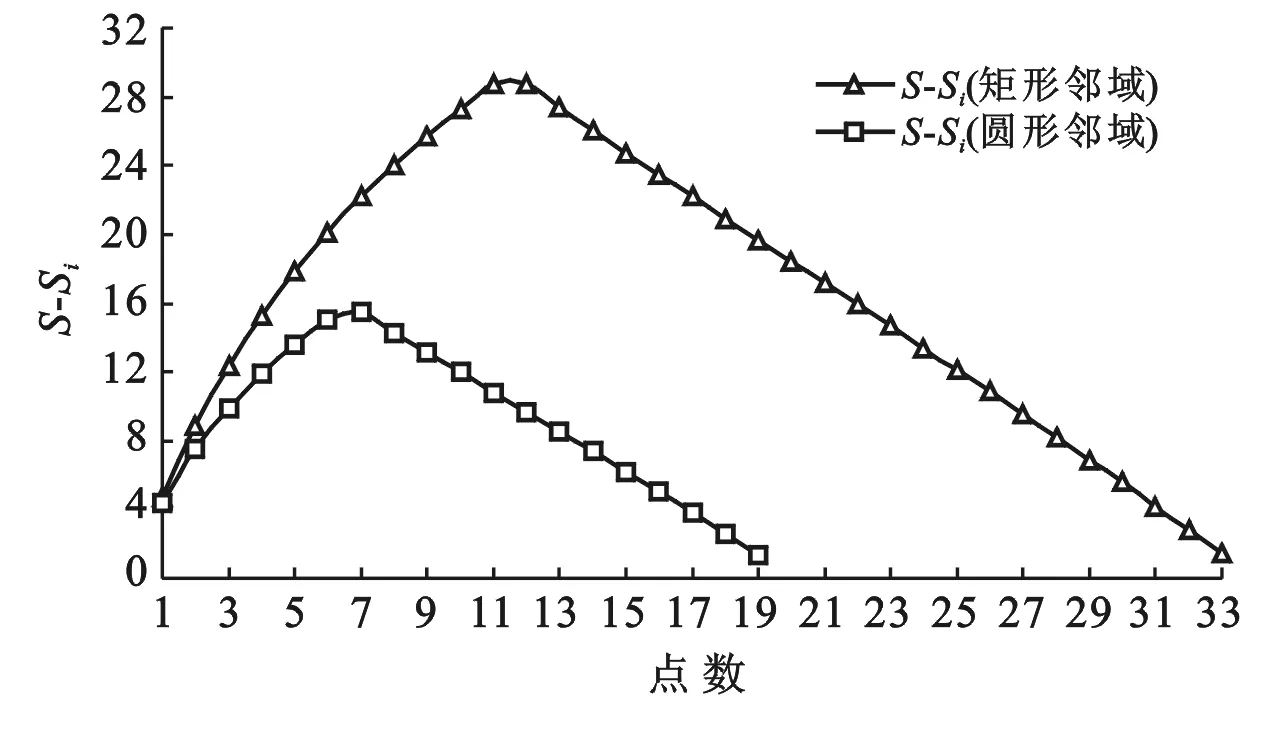
图3　S与Si差值的变化曲线

矩形邻域和圆形邻域的多尺度地形起伏度计算方法十分类似，只是邻域范围的设定方法有所不同，最佳尺度所对应的面积相差0.355 487 km2。由附图12可看出，平原、丘陵、山地的分界线清晰可见，陕西省地形起伏度以小、中起伏为主，微起伏次之；小起伏主要分布在陕北及铜川、咸阳及宝鸡北部一带，汉中、商洛及安康地区分布较少；中起伏主要分布在陕南地区、关中西南地区，在咸阳、延安地区和宝鸡地区北部一带均有分布，但较少；大起伏主要分布在陕南一带。

从表4可看出，最佳尺度地形起伏度各种类型所占面积比例十分接近，只是最佳计算单元大小为12×12时，其平坦、微起伏及小起伏所占面积比例比R=8时大一些，而其他起伏所占面积比例小一些。小起伏山地和中起伏山地的总面积占研究区面积的2/3之余，平坦面积占研究区面积的1/10之余，而微起伏与大起伏山地所占比例相当，面积比例都较小，极大起伏山地所占比例最小，在矩形邻域下像元仅有83个，这说明研究区局部地形起伏度较大，主要以中、小起伏为主，总体上地形较平缓，多为平原、丘陵及小起伏山地。

表4　各级地形起伏度所对应的像元数及面积百分比

4讨论与结论

(1) 利用邻域分析法提取不同矩形窗口和圆形窗口下的地形起伏度，并统计不同矩形窗口和圆形窗口下的每种地形起伏度类型所占面积比例，分析得出不同地形起伏度类型所占面积比例的变化各有不同。

(2) 对邻域面积与平均地形起伏度进行对数方程拟合，从拟合曲线(图2)得知，拟合效果较好，且圆形邻域面积与其平均起伏度的拟合效果要比矩形邻域的好，这意味着圆形邻域下地形起伏度划分的结果较矩形邻域更接近实际面积，但还需要进一步研究。

(3) 运用均值变点分析法确定了地形起伏度的最佳计算单元，该方法清晰直观、易于分析，对只有1个突变点的检验最有效，其结果也较为理想。通过此方法得到陕西地区按矩形邻域窗口计算的地形起伏度最佳尺度为12×12(898 704 m2)；按圆形邻域计算的地形起伏度最佳尺度为R=8(1 254 191.4 m2)，圆形邻域有别于矩形邻域。

(4) 利用最佳计算单元输出陕西地形起伏度分级图，通过统计分析，可知陕西地区以小起伏、中起伏为主，二者总面积占研究区面积的2/3之余，这说明地形起伏整体较平缓，多为平原、丘陵及小起伏山地。

[参考文献]

[1]彭珂珊.水土流失是生态环境恶化的根源[J].地质灾害与环境保护,2001,12(2):25-31.

[2]中华人民共和国水利部.全国水土流失公告[R].北京:中华人民共和国水利部,2002.

[3]王占礼.中国土壤侵蚀影响因素及其危害分析[J].农业工程学报,2000,16(4):32-36.

[4]刘新华,杨勤科,汤国安.中国地形起伏度的提取及在水土流失定量评价中的应用[J].水土保持通报,2001,21(1):57-59.

[5]涂汉明,刘振东.中国地势起伏度最佳统计单元的求证[J].湖北大学学报:自然科学版,1990,12(3):266-271.

[6]徐天献,王玉宽,傅斌.汶川地震重灾区土壤侵蚀敏感性评价[J].中国水土保持,2011(1):39-42.

[7]祁元,刘勇,杨正华,等.基于GIS的兰州滑坡与泥石流灾害危险性分析[J].冰川冻土,2012,34(1):96-104.

[8]马晓微,杨勤科.基于GIS的中国潜在水土流失评价指标研究[J].水土保持通报,2001,21(2):41-44.

[9]闫满存,李华梅,王光谦.广东沿海陆地地质环境质量定量评价研究[J].工程地质学报,2000,8(4):416-425.

[10]高守英,吴泉源,安国强.基于GIS的龙口市泳汶河流域地貌形态定量分析[J].遥感技术与应用,2003,18(2):87-90.

[11]唐飞,陈曦,程维明,等.基于DEM的准噶尔盆地及其西北山区地势起伏度研究[J].干旱区地理,2006,29(3):388-392.

[12]王玲,吕新.基于DEM的新疆地势起伏度分析[J].测绘科学,2009,34(1):113-116.

[13]王岩,刘少峰.基于DEM的青海贵德地区地形起伏度的研究[J].地质通报,2008,27(12):2117-2121.

[14]曹伟超,陶和平,孔博,等.基于DEM数据分割的西南地区地貌形态自动识别研究[J].中国水土保持,2011(3):38-41.

[15]郎玲玲,程维明,朱启疆,等.多尺度DEM提取地势起伏度的对比分析:以福建低山丘陵区为例[J].地球信息科学,2007,9(6):1-6.

[16]陈述彭,鲁学军,周成虎.地理信息系统导论[M].北京:科学出版社,1999:15-75.

[17]中国科学院地理研究所.中国1∶1000000地貌图制图规范(试行)[M].北京:科学出版社,1987:33-34.

收稿日期：2015-10-26修回日期：2015-12-01

通讯作者：常庆瑞(1959—),男(汉族),陕西省子洲县人,硕士,教授,博导,主要从事资源环境与“3S”技术应用研究。E-mail:changqr@nwsuaf.edu.cn。

文献标识码：B

文章编号：1000-288X(2016)03-0265-06

中图分类号：P931, S157

A Study on Optimal Statistical Unit for Relief Amplitude of Land Surface in Shaanxi Province

CHEN Xuexiong1, ZHANG Xiaojun2, CHANG Qingrui3

(1.CollegeofResourcesandEnvironment,ShanxiAgriculturalUniversity,Taigu,Shanxi030801,China; 2.CollegeofHorticulture,ShanxiAgriculturalUniversity,Taigu,Shanxi030801,China;3.CollegeofNaturalResourcesandEnvironment,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)

Abstract：[Objective] To determine the optimal statistical unit, analyze the spatial distribution of topographical relief in Shaanxi Province in order to provide basic data for the classification of geomorphic types. [Methods] Based on the 90 m resolution SRTM(shuttle radar topography mission)， DEM (digital elevation model data), the relief amplitude of Shaanxi Province was extracted with neighborhood statistics analysis. We selected 34 rectangular neighborhood windows (2×2, 3×3,4×4,…,35×35) and 20 circular neighborhood windows(the radius ranged from 2 to 21 ), and calculated the ratio of relief amplitude at different rectangular windows and circular windows. The optimal calculation unit was calculated by using the mean change-point analysis method. Classification map of relief amplitude in Shaanxi Province was obtained, and the features of relief amplitude were analyzed. [Results] The ratios of different topographic relief types varied greatly. The optimal statistical unit at rectangular neighborhood was 12×12, with an area of 898 704 m2, while the optimal statistical unit at circular neighborhood was R=8, with an area of 1 254 191.4 m2, indicating that the circular neighborhood was different from the rectangular neighborhood. Generally, the terrain in Shaanxi Province was relatively flat, and the relief amplitude was mainly at small and medium level. [Conclusion] The mean change-point analysis is an ideal method to determine the optimal statistical unit.

Keywords:soil erosion; shuttle radar topography mission; digital elevation model; relief amplitude; best calculation unit; Shaanxi Province

资助项目：山西农业大学引进人才博士科研启动项目“多尺度DEM提取地形起伏度的对比分析：以山西省为例”(2014YJ02); 国家“863”计划项目(2013AA102401-2)

第一作者：陈学兄(1986—),女(汉族),青海省乐都县人,博士,讲师,主要从事基于GIS的水土流失评价研究。E-mail:chenxx0505@126.com。