无穷区间上多点边值问题多个正解的存在性

李梦菲（山东协和学院，山东 济南 250000）



无穷区间上多点边值问题多个正解的存在性

李梦菲
（山东协和学院，山东 济南 250000）

摘 要：利用Leggett-Williams 不动点定理，研究无穷区间边值问题.的多个正解的存在性

关键词：边值问题；正解；不动点

1 引言

在本文中，我们利用Leggett-Williams不动点定理讨论了问题

（H1）p（t）∈C［0,∞）；p（t）＞0,t∈（0,∞）且在［0,∞）任意有界子区间上可积

（H2）f：［0,∞）×［0,∞）×R→［0,∞）是连续的

记x（t）=（1+t）y1（t）,x'（t）=y2（t）,f（t,x,x'）=g（t,y1,y2）

2 预备知识

引理1 对任意常数0＜a*＜b*＜∞都存在0＜c*＜1,使得

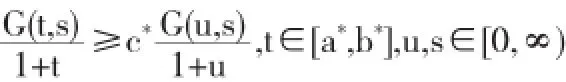
我们称一个泛函α在P上非负连续的凹泛函，如果α：P→［0,∞）是连续的，且对所有x,y∈P和0≤λ≤1有α（λx+ （1-λ）y）≥λα（x）+（1-λ）α（y）成立.

令0＜a＜b,r＞0为常数，P和α如上所定义，再定义Pr｛xP|||x||1＜r｝，P（α,a,b）=｛x∈P|a≤α（x）,||x||1≤b｝.

定理1［1］（Leggett-Williams不动点定理）设P是BanachE空间E上的一个锥.α是P上非负连续凹泛函，T：Pc→Pc是全连续的，假设存在正数0＜a＜b＜d≤c使得下列条件成立

（C1）｛x∈P（α,b,d）|α（x）＞b｝≠Ø,且对x∈P（α,b,d）有α（Tx）＞b.

（C2）||Tx||1＜a,∀||x||1≤a.（C3）∀x∈P（α,b,d）满足||x||1＞d,有α （Tx）＞b.

则 T至少有三个不动点 x1,x2,x3使得||x1||1＜a.b,α（x2）, ||x3||1＞a,且α（x3）＜b.

3 主要结果

设P上算子T：

则算子T的不动点x（t）就是BVP（1）的解

引理2［2］设M⊆Cl（［0,∞）,R）,则M在Cl（［0,∞）,R）中是相对紧的，当且仅当（a）M在Cl中一致有界，（b）对M中任意x（t）在［0,∞）上局部等度连续，（c）对M中任意x（t）在t=∞点等度连续，即∀ε＞0,∃T＞0,当t≥T时，有|x（t）-x（∞）|＜ε,∀x∈M.

引理3 算子T：P→P是连续的

证明 由f的非负性知（Tx）（t）≥0,且∀x∈P由于（H3）有

所以（Tx）（t）∈E.另外，由引理1可知t∈［a*,b*］时，对于∀u∈［0,∞）

下证T是连续的.设｛x0｝⊆P,x0∈P,满足||xn-x0||1→0,（n→∞）.从而∃M＞0,s.t||xn||1≤M.由控制收敛定理得

于是||Txn-Tx0||1→0,（n→∞）.T：P→P是连续的.

引理4 算子T：P→P是紧的

证明 设Ω⊆P为任意有界集.从而∃M＞0,s.t||x||1≤M, ∀x∈Ω.当x∈Ω时根据（2）（3）式易知T在Ω上是一致有界的.

另一方面∀T＞0,若t1,t2∈［0,T］,∀x∈Ω由于（H3）,当t1→t2时有

由T的任意性知，T在［0，∞）局部等度连续的，∀x∈Ω, 有

定理2 设（H1）-（H3）成立,并设存在常数0＜2m＜a＜b＜c*c,使得

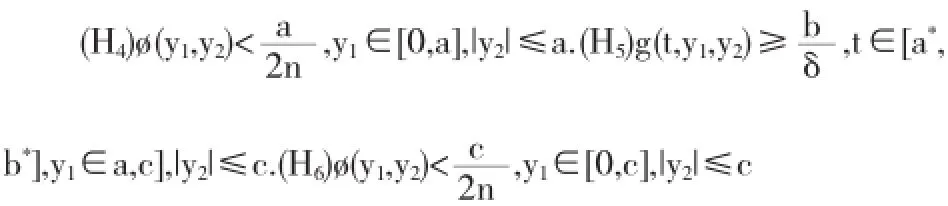
则BVP（1）至少有三个正解x1,x2,x3,满足||x1||1＜a.b＜α（x2）, ||x3||1＞a,且α（x3）＜b

证明 引理3，4知,T：P→P是全连续的,又由α的定义得，α*（x）≤||x1||1,∀x∈P.下面证明定理1中条件都满足.

由（H）5有g（t,y1,y2）≥,t∈［a*,b*］,y1∈［a,］,|y2|≤.现取x∈P（α,b,）则b≤≤,x'（t）≤,t∈［a*,b*］.于是

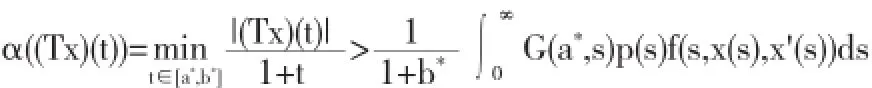
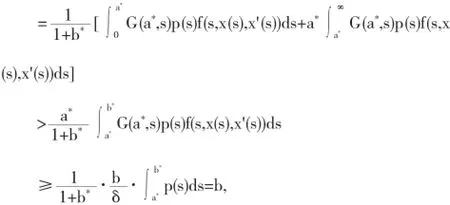
最后验证定理1中条件（C3）成立.假设x∈P（α,b,c）满足||Tx||＞.分两种情况讨论.

1

所以α（Tx）≥c*||Tx||0＞c*=b.

2）||Tx||1=||Tx||，则由（H5）得，

参考文献：

〔1〕Leggett R,Williams L.Multiple positive fixed points of nonlinear operators on ordered banach spaces.Indiana University Math.J.,1979,28：673-688.

〔2〕Corduneanu C.Integral Equation and Stability of Feedback Systems.Academic Press,New York,1973.

中图分类号：O175.8

文献标识码：A

文章编号：1673-260X（2016）05-0001-03

收稿日期：2016-03-24

基金项目：“山东协和学院科技计划项目”课题（XHXY201506）阶段性成果