序约束下一类指数分布族参数的Bayes估计

王秋平

（昌吉学院数学系　新疆　昌吉　831100）



序约束下一类指数分布族参数的Bayes估计

王秋平

（昌吉学院数学系新疆昌吉831100）

摘要：在平方损失和熵损失函数下，分别讨论序约束下先验分布选取杰佛莱准则时两个单参数指数分布族总体参数的Bayes估计，进而给出了序约束下不同损失函数时的两个单参数指数分布族总体参数精确的Bayes估计形式，并证明了该估计的容许性。

关键词：序约束；Bayes估计；平方损失；熵损失

近年来对序约束下多总体参数估计的研究文献很多，参考文献［1］给出了序约束下伽马分布、泊松分布以及二项分布参数的Bayes估计，参考文献［2］讨论了序约束条件下，不同先验分布时，平方损失和熵损失函数下两个几何总体参数的Bayes估计，参考文献［3］探讨了序约束下当选取熵损失和对称熵损失函数时，两个Burr分布总体参数的Bayes估计，参考文献［4］给出了序约束下两Pareto总体参数的Bayes估计。而将序约束的条件与指数分布族相关联的文献还很少涉及，本文将在平方损失和熵损失函数下，讨论一类单参数指数分布族中总体参数在序约束下的Bayes估计。该指数分布族包含了常见的几大分布，如，伽马分布、帕累托分布以及威布尔分布等，在工业、可靠性等领域应用广泛，因此对其研究具有一定的实际意义和理论价值。

1　先验分布的选取

本文讨论形如［5］

的一类单参数指数分布族中（其中k＞0，c为归一化常数）未知参数θ在半序约束条件下的贝叶斯估计。

设两样本总体X，Y均服从密度函数为（1）式的分布，其密度分别为分别为来自于实直线的某个子集，根据实际问题所提供，有

根据参考文献［3］，本文（θ1，θ2）在约束条件（2）下，当两样本总体的先验分布选为杰佛莱准则下的先验分布时，此时的（θ1，θ2）的先验密度为

2　参数（θ1，θ2）的Bayes估计

一般地，两个总体的平方损失函数定义为

引理1［6］在平方损失函数（4）下，对任何先验分布，当两总体分布为（1）时参数（θ1，θ2）的Bayes估计为后验期望向量

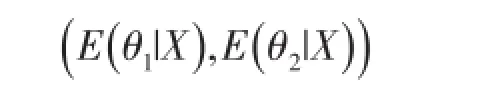
一般地，两个总体的熵损失函数定义为

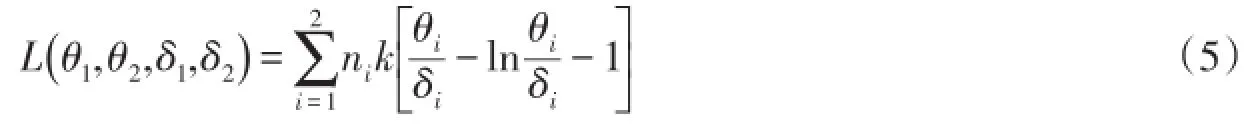
引理2［7］在熵损失函数（5）下，对任何先验分布，当两总体分布为（1）时参数（θ1，θ2）的Bayes估计为

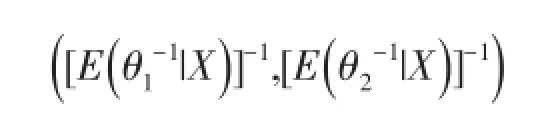
证明过程见参考文献［3］定理1，此处略。

3　序约束下参数（θ1，θ2）的Bayes估计

3.1平方损失下总体参数的Bayes估计

定理1在平方损失（4）下，先验分布为（1）式，则在约束（2）下两个指数族分布总体参数（θ1，θ2）的后验期望为

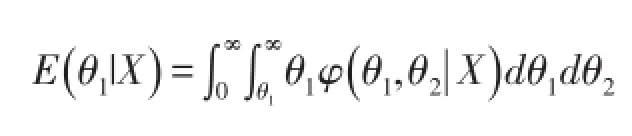
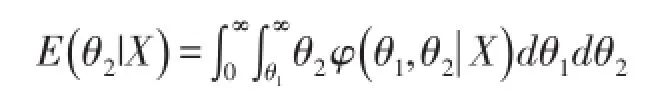
其中

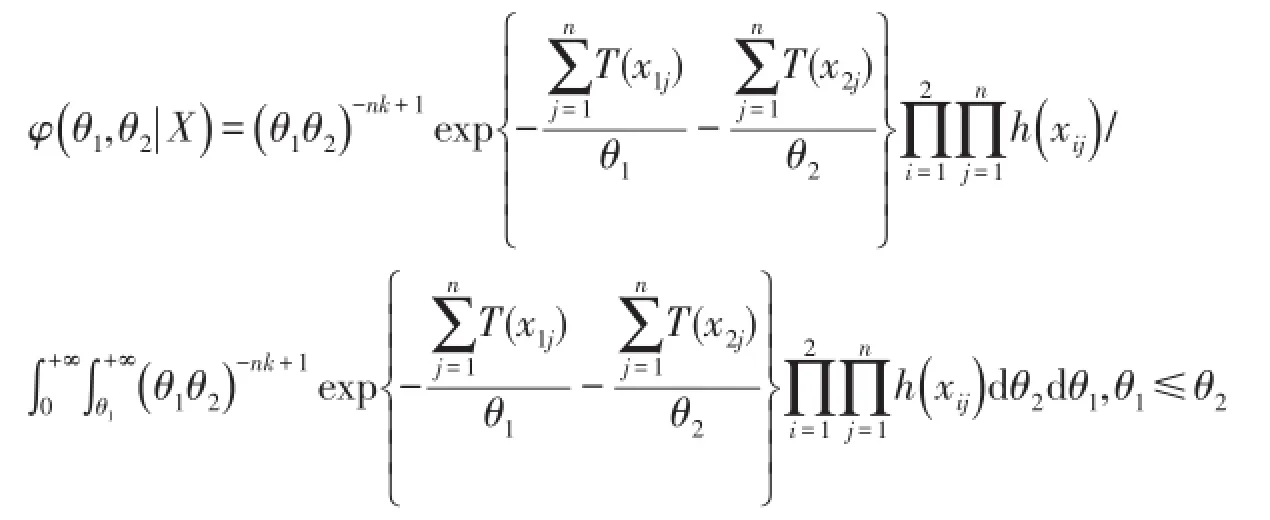
证明：先求X的边际密度和后验密度，然后再求后验期望。因X是来自同一单参数指数分布族总体，且相互独立，即有X关于的条件密度为

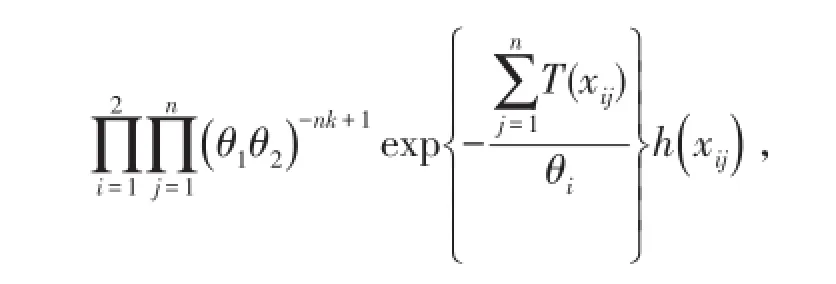
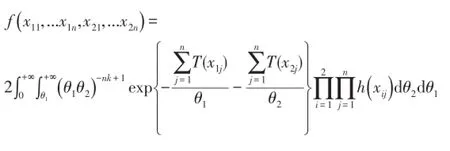
由条件密度公式知，此时（θ1，θ2）的后验密度为

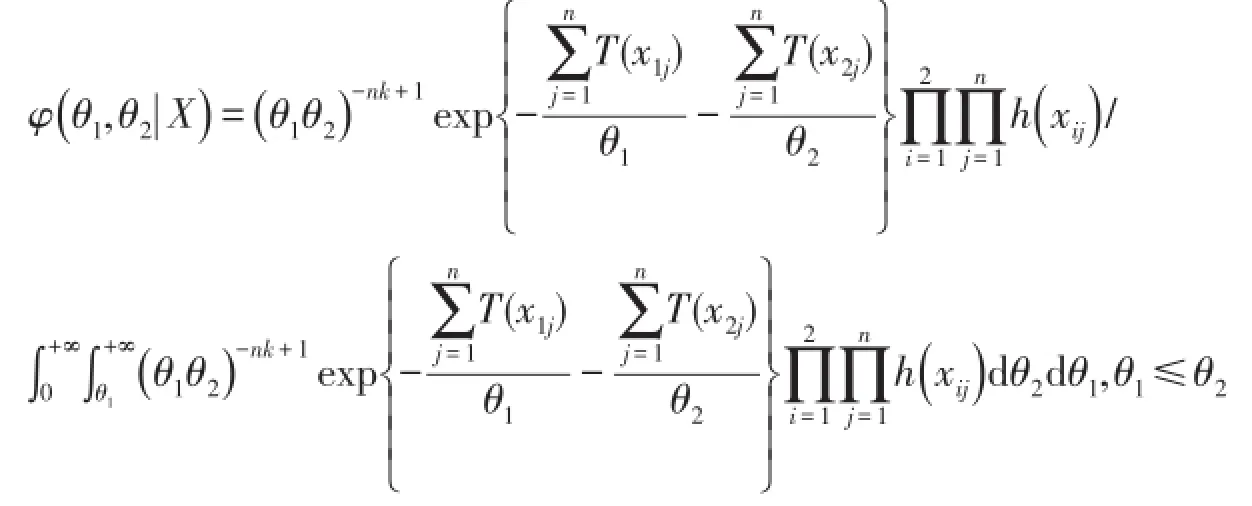
于是有

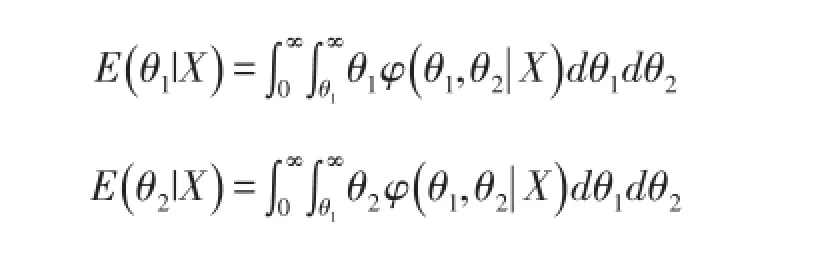
定理2在熵损失函数（5）式下，先验分布为（1）式，则在约束（2）下两个指数分布族总体参数（θ1，θ2）的Bayes估计为

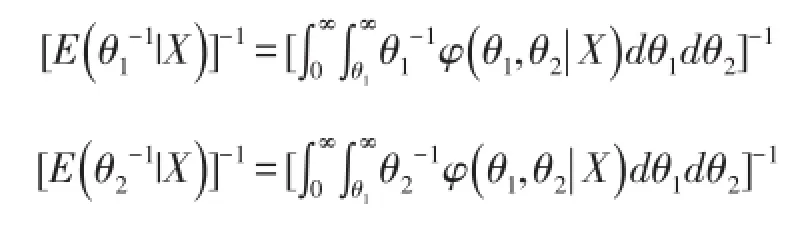
证明：证明过程同定理1类似，篇幅过长，此处略。

4　井估计的容许性

引理3［8］设，统计判决问题的损失函数为，参数θ的先验分布为，那么：

（1）若损失函数L（ ）θ，δ关于δ为严凸函数，则该统计判决问题的Bayes解几乎处处唯一。

（2）若θ的Bayes估计是唯一的，则它是容许的。

容许估计。

证明：同定理3，此处略。

参考文献：

［1］［6］赵世舜，宋立新，高秋阳.序约束下两样本总体参数的Bayes估计［J］.吉林大学学报（自然科学版），1998，1（1）：19-23.

［2］［7］周伟萍，张德然，杨兴琼.序约束下两个几何总体参数的Bayes估计［J］.山东理工大学学报（自然科学版），2007，21（6）：35-37.

［3］［8］柴媛媛，宋立新，等.序约束下两个Burr分布总体参数的Bayes估计［J］.渤海大学学报（自然科学版），2009，30 （3）：242-244.

［4］李艳颖.序约束下两Pareto分布总体参数的Bayes估计［J］.廊坊师范学院（自然科学版），2009，9（3）：16-19.

［5］张娅莉，查新月.一类指数分布族的参数估计问题［J］.南阳师范学院学报，2007，（6）：22-24.

中图分类号：O212.5

文献标识码：A

文章编号：1671-6469（2016）03-0121-04

收稿日期：2016-04-05

基金项目：昌吉学院科研项目“序约束下一类指数分布族参数的贝叶斯估计”（2014SSQD006）。

作者简介：王秋平（1986—），女，吉林榆树人，昌吉学院数学系讲师，研究方向：统计、金融。