基于RQA与SVM的声发射信号检测识别方法

司　莉， 毕贵红， 魏永刚， 陶　然， 张寿明

(1.昆明理工大学 信息工程与自动化学院，昆明　650500；2.昆明理工大学 电力工程学院，昆明　650500；3.昆明理工大学 冶金与能源工程学院，昆明　650093；4.云南省特种设备安全检测工程技术研究中心，昆明　650050)



基于RQA与SVM的声发射信号检测识别方法

司莉1,4， 毕贵红2,4， 魏永刚3,4， 陶然4， 张寿明1

(1.昆明理工大学 信息工程与自动化学院，昆明650500；2.昆明理工大学 电力工程学院，昆明650500；3.昆明理工大学 冶金与能源工程学院，昆明650093；4.云南省特种设备安全检测工程技术研究中心，昆明650050)

摘要：针对裂纹声发射信号检测问题，提出基于递归定量分析与支持向量机相结合的新型检测方法。利用小波阈值去噪原理，对采集的声发射信号进行去噪，将递归定量分析引入声发射信号检测，提取递归定量分析的量化特征参数，结合支持向量机对模拟裂纹声发射信号进行识别。并实验验证该方法的可行性。

关键词：声发射信号；小波阈值去噪；递归定量分析；支持向量机

各类压力管道、高压锅炉使用过程中由于腐蚀、磨损等原因会造成材料破损导致泄漏，一旦泄漏点不能及时处理，极易发生工业事故，造成严重的经济损失及人员伤亡。通常泄漏发生前材料内部产生裂纹，断裂部分内部应力超过屈服极限进入不可逆的塑性变形阶段，产生瞬态弹性波形，即声发射(Acoustic Emission，AE)[1]，对检测的声发射信号进行分析处理，可获得早期裂纹大量信息，以便及时采取措施。因此，研究可靠的声发射信号检测识别技术具有重要意义。

裂纹声发射信号为具有一定频域、非平稳非线性突发型信号。对此类信号处理的时域参数法、时域波形发、频域法、小波分析及检验模态分解等均从不同角度描述该信号特征，提供诸多声发射信号检测方法。文献[2]利用声发射技术对管道泄漏检测进行试验研究，通过时频分析实现对泄漏信号识别。文献[3]利用高压泄漏检测实验装置采集泄漏及各种干扰音波信号，进行时、频域及时频域结合的综合分析，降低音波泄漏检测的误报率。文献[4]利用小波分包分析方法提取分解后各频带能量作为特征向量，输入神经网络分类器进行分量。文献[5]在海洋模拟平台实验中利用Nielson源测试法(断铅法)模拟产生裂纹测试信号，用敲击及砂纸摩擦模拟背景声发射信号，以局域波法提取裂纹声发射信号各频带能量作为神经网络输入的特征参数，有效识别海洋平台结构声发射信号。文献[6]在退役的混流水轮机上利用断铅法模拟裂纹声发射信号，用基于BP神经网络的智能定位方法定位混流式水轮机裂纹声发射源。文献[7]利用SVD、Fast Kurtogram算法对滚动轴承声发射故障进行有效识别。文献[8-11]对此种模拟裂纹声发射信号进行基于小波包分析的声发射信号界面衰减规律、小波神经网络定位、基于核主成分分析及支持向量机的源定位及对裂纹信号进行稀疏编码等研究。

递归图即将相空间中递归状态可视化，直观表示高维相空间中轨迹的递归关系[12]。Zbilut等[13]通过测定递归图中基本图形点及线段分布，提出量化递归图方法，即定量递归分析 (Recurrence Quantification Analysis, RQA)，且已广泛用于各种非线性非平稳信号检测与诊断中，如脑电信号、心音信号、语音信号、泄漏电流信号等，并取得良好效果。

支持向量机(Support Vector Machine, SVM) 即在统计学习理论基础上发展的通用学习机器。基于结构风险最小化准则计算实际风险，能有效提高算法泛化能力，为处理有限样本学习的有效工具[14]。

鉴于RQA在脑电、心因、语音等非平稳信号处理中的成功应用，本文提出新的声发射信号检测识别方法，即将非平稳信号处理方法RQA引入声发射信号检测，结合SVM对模拟声发射信号进行识别。利用小波阈值去噪原理，对采集的声发射信号去噪，提取RQA 量化特征参数作为SVM 输入参数，实现对声发射信号检测识别。

1小波阈值去噪

小波分析即用Mallat塔式算法对信号进行降阶分解。该算法在每尺度下将信号分解成概貌分量与细节分量。信号s(t)的分解过程由j+1～j尺度逐步分解，分解公式为

小波去噪实质为抑制信号中无用部分、增强有用部分过程。该过程的几个步骤为：① 分解过程，即选定一种小波对信号进行n层小波分解。② 作用阈值过程，即对分解的各层系数进行阈值处理，获得估计小波系数。③ 重构过程，据去噪后小波系数进行小波重构，获得去噪信号。小波阈值去噪过程见图1。

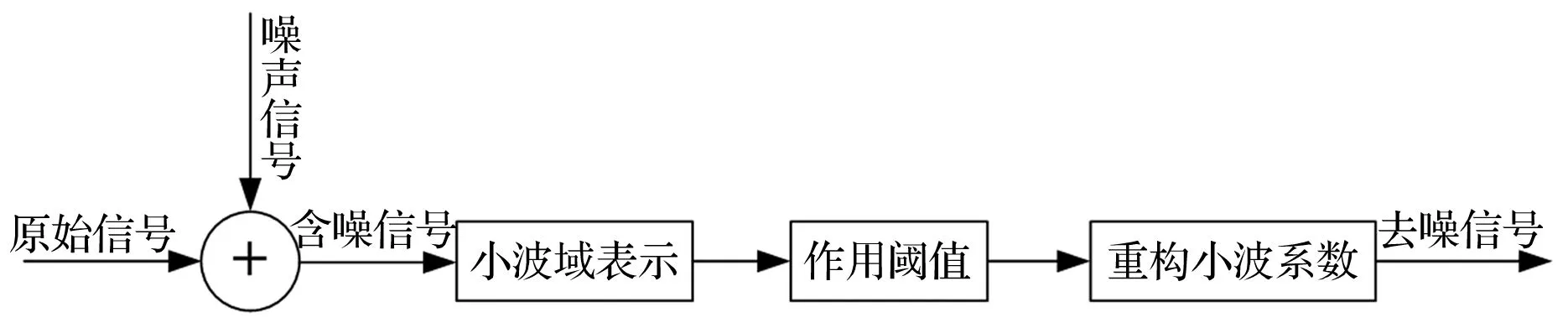
图1　小波阈值去噪过程Fig.1 Process of wavelet threshold de-noising

基于小波分析阈值去噪关键在于阈值门限选取，某种程度上关系到信号去噪的质量。不同小波系数估计方法，对应不同阈值去噪方法，即硬、软阈值方法。硬阈值函数的表达式为

(1)

软阈值函数表达式为

(2)

硬阈值函数为不连续函数，数学上不易处理，会产生间断点；而软阈值函数为连续函数，能较好克服此种缺点。

从实测声发射信号中截取长度1 000点一段信号，选小波函数db3，分解层数为5层，对信号进行去噪。结果见图2。可见去噪后断铅信号波形较光滑，并保留声发射信号的主要特征成分。

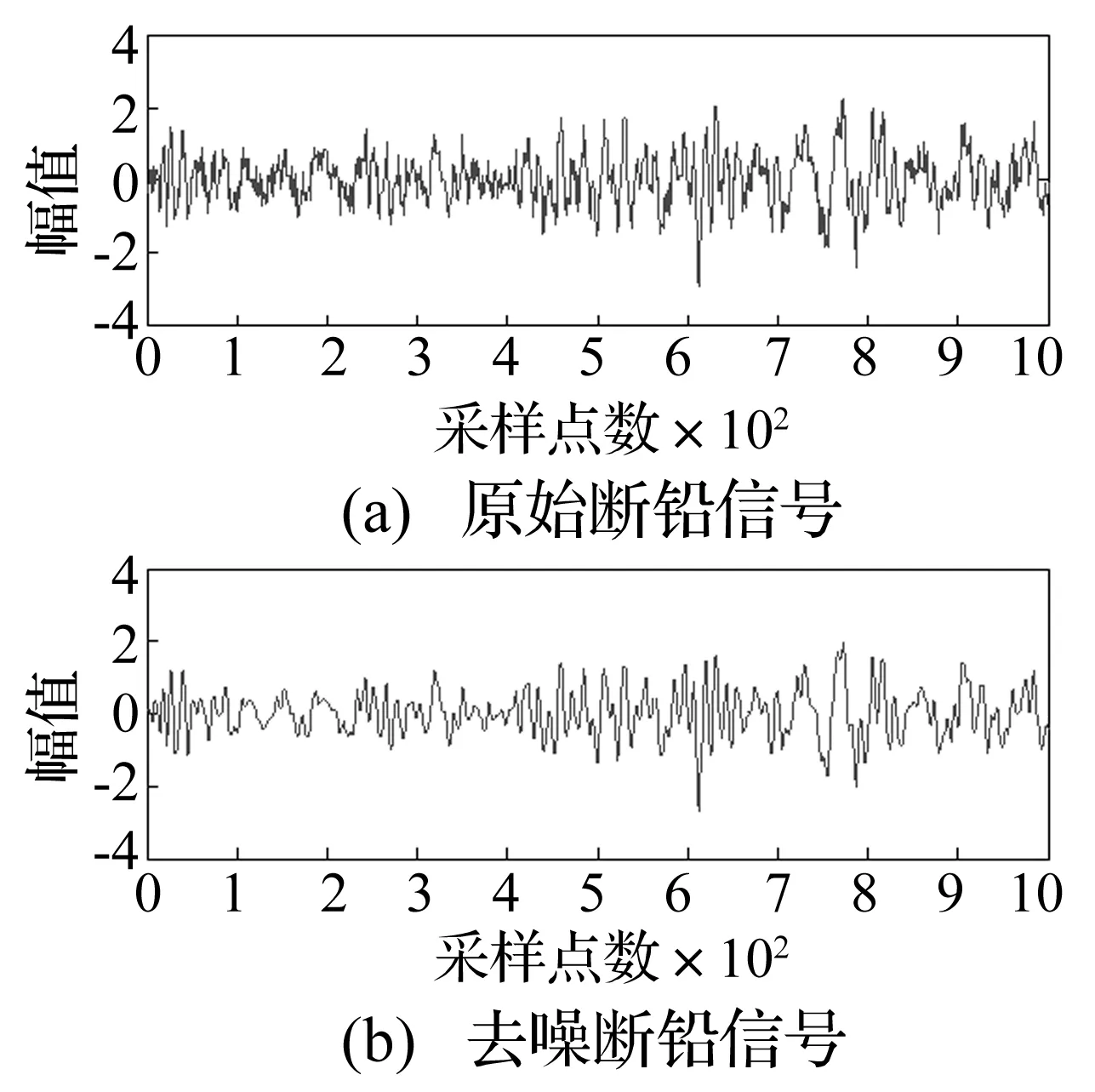
图2　小波去噪实验结果Fig.2 Experimental result of wavelet de-noising

2基于递归分析的特征参数提取

2.1递归图

递归图作为将重构相空间中递归状态以可视化方式呈现的绘图方法，通过提取系统中时间序列，重现系统递归行为。在递归图中，i、j时刻递归状态通过二维方阵中黑点或白点表示，其中黑点表示坐标横轴、纵轴对应的状态发生递归现象，白点表示不发生递归现象，二者形成的拓扑、纹理结构能较好揭示系统的内在状态，从而对系统进行定性分析。递归图具体算法为：

(1) 对采集的时间序列用Takens理论、C-C算法选取恰当嵌入维数m及时间延迟τ，重构的时间序列为

(3)

(2) 计算重构时间序列中第i点xi、第j点xj的距离，即

(4)

(3) 计算递归值

(5)

式中：εi为阈值常数，可选固定值，使半径为εi的球中含一定邻域数；H(x)为Heaviside函数。

(4) 在以i为横坐标、j为纵坐标图中绘制R(i,j)(i、j称时间序列标号)，从而得到递归图。

据递归图计算过程知，阈值εi的取值对递归图影响较大，其大小直接决定递归图中所含递归点数量。选择阈值主要方法有：① 阈值约为原始信号标准差的25%；② 阈值为相空间直径的10%；③ 按噪声选阈值为信号中可测噪声标准差的5倍。

2.2递归定量分析参数

为从递归图中得到更丰富信息，Zbilut等通过测定递归图中基本图形点及线段分布，提出量化递归图方法，定量表征递归图结构特征，即定量递归分析。主要包括7种特征参数，即递归率、确定率、最长对角线、熵、趋势、层流率及平均垂直线段长度。有诸多研究对比率(Ratio)、平均重标距离(Mean Rescaled Distance)、分叉性(Divergence)等参数进行补充定义，完善对递归图的量化分析。

2.2.1递归率

递归率(Recurrent Rate,RR)指递归图平面中递归点占平面可容纳总点数百分比，表明m维相空间中邻近相空间点所占比例，表达式为

(6)

2.2.2确定率

确定率(Determinism,DET)指递归图中构成沿对角线方向线段递归点占总递归点百分比，可将递归图中孤立的递归点与有组织形成连续对角线方向线段递归点进行区分，通过对角线长度分部特征可大致分析出系统确定性特征，表达式为

(7)

式中：p(l)为l长度线段数。

2.2.3最大对角线长度

最大对角线长度(Maximum Length,Lmax)指除主对角线外，对角线方向线段长度最大值，表达式为

Lmax=max(li)

(8)

2.2.4熵

熵(Entropy，ENTR)反映递归图中对角线方向线段频次分布，揭示系统确定件结构复杂性，表达式为

(9)

2.2.5递归趋势

(10)

2.2.6层流率

层流率(Percent Laminarity，LAM)与确定率相似，指递归图中沿垂直/水平方向线段递归点占总递归点百分比，即

(11)

式中：p(v)为v长度垂直/水平线段分布概率；vmin为最小分析长度，一般取2。

2.2.7平均垂直线段长度(Trapping Time，TT)

(12)

3支持向量机

3.1支持向量机原理

SVM为在统计学习理论基础上发展的通用学习机器，基于结构风险最小化准则计算实际风险，能有效提高算法的泛化能力，是处理有限样本学习的有效工具。基本思想即寻找原空间或经投影的高维数空间中最优分类平面，该平面能将两类训练样本无误分开，且使分类空隙最大。

对线性可分样本集(xi,yj)(i=1,2,…n)，x∈Rd，yj∈{-1,+1}。分类线方程可表示为wTx+b=0，将其归一化，使样本集满足约束条件为

yi(wTxi+b)-1≥0，(i=1,2,…n)

(13)

(14)

式(13)中使等号成立的样本称支持向量，两类样本的分类空隙为2/‖w‖。在约束条件下最优分类面问题可表示为约束优化问题，即求函数式(14)的最小值。为此，可定义Lagrange函数为

式中：αi≥0为Lagrange系数，由此将原问题转化为凸二次规划的对偶问题，即

(16)

(17)

f(x)=sgn[(w*)Tx+b*]=

(18)

式中：sgn()为符号函数。

对线性不可分样本，将输入向量映射到一高维数的特征空间，寻找能将特征空间分为两个区域的最优超平面，通过定义核函数，利用原空间核函数取代高维数特征空间中内积运算，即K(xi,xj)=φ(xi)φ(xj)，避免维数灾难。当用一个超平面不能将两类点完全分开时(只有少数点被错分)，可引入松弛变量ξi及惩罚参数C，将寻找最优分类面问题转化为

(19)

最优分类函数可表示为

f(x)=sgn[(wTx+b]=

(20)

3.2多分器构造

SVM算法最初为二值分类问题设计，处理多类问题时则需构造合适的多类分类器。构造SVM多类分类器方法主要有直接法及间接法。前者直接在目标函数上进行修改，将多个分类面参数求解合并到一个最优化问题中，通过求解该最优化问题“一次性”实现多类分类。此方法看似简单，但计算复杂度较高，实现较困难，只适于小型问题；后者则通过组合多个二分类器实现多分类器构造，常见方法有“一对多”、“一对一”两种[16]。 一对多法，即在训练时依次将某个类别样本归为一类，剩余样本归为另一类，n个类别样本构造出n个SVM分类器。对测试样本分类时输出结果为具有最大分类函数值的那类。缺点为训练样本大，训练困难，推广误差无界。一对一法，即在任意两类训练样本间设计一个SVM分类器，n个类别样本需设计n(n-1)/2个SVM分类器。对测试样本进行分类时，用测试样本询问每个两类分类器，获得n(n-1)/2个分类结果，再用投票法决定测试样本所属类别。本实验所用台湾大学的libsvm工具箱即据该方法实现[17]。以3分类问题说明分类过程，原理见图3。

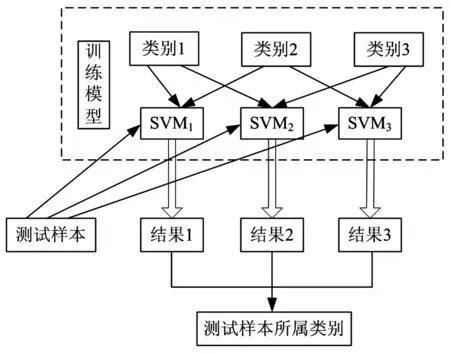
图3　多分类器构造原理Fig.3 Schematic structure of multiple classifiers

4基于RQA与SVM声发射信号检测分类方法

基于RQA与SVM的声发射信号检测识别方法流程见图4。实际声发射信号检测过程中常伴有高频随机信号，影响检测及信号处理效果，因此，需在信号处理初期有效除去随机噪声信号。本文采用较成熟的小波软阈值去噪方法，对采集的声发射信号进行噪声去除，并将去噪后信号经定量递归分析计算获得一系列特征参数，选择性将特征参数作为SVM分类器输入值，实现对采集信号的检测分类。

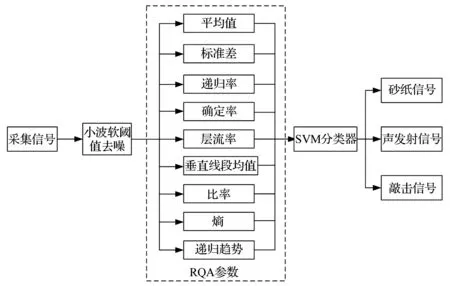
图4　声发射信号检测识别方法流程Fig.4 Process of acoustic emission detection and identification

5实验装置及实验结果

5.1实验装置

采用北京声华兴业科技有限公司的SAEU2S 数字声发射系统采集试验数据。该系统可实现最大30 MB/s连续波形数据、40 万组/s连续特征参数传输速率，可充分满足现场及实验室各种要求。该系统见图5。金属压力管道裂纹声发射信号频率主要分布在几十～几百kHz，实验所用传感器型号为谐振频率150 Hz的SR150 M传感器，设置采样频率2 000 kHz，采样长度10 ms，参数间隔2 ms，闭锁时间1 ms，波形门限50 DB。

实验时保持传感器与事故点位置不变，在事故点分别模拟包括断铅信号在内的三种工况声源，记录实验数据。为验证方法的有效性，在实验室中按国际无损检测界规定，用0.5 mmHB铅笔芯进行断铅试验，获得模拟裂纹声源；用砂纸、金属棒，在相同断铅位置模拟出另外两种不同工况声源。测量管道见图6。

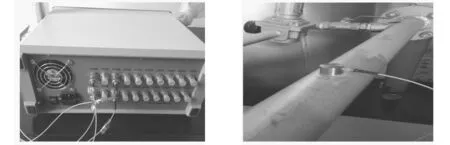
图5 声发射信号采集装置Fig.5Signalacquisitiondeviceofacousticemission图6 模拟声发射源Fig.6Sourceofsimulatedacousticemission

5.2实验验证及分析

实验共采集断铅、砂纸及敲击信号各10组，总计30组数据。采样频率及时间决定每帧波形采样点数为2×104，从3类信号中随机各选1个波形样本及频谱，见图7。图中敲击信号为一次金属棒敲击采集信号，敲击发生点即为波形图对应的突变点，由于声发射信号反射叠加在波形图中形成多个突变毛刺。敲击信号频率范围较窄，分布在0～180 kHz内，主要能量集中在40 kHz。砂纸信号幅值较小，且均匀分布，其能量范围为10～400 kHz，在约40 kHz、180 kHz出现能量峰值，180 kHz处波峰更小。断铅信号幅值较其它两类信号幅值大，频率主要分布在10～300 kHz，在50 kHz附近能量幅值较大，200 kHz处有较小峰值。

图7　不同类型信号波形及频谱图Fig.7 Waveforms and spectrum map of different signals

在采集的数据样本中，从起始端取1 500个点进行递归分析，获得不同类型声发射源信号递归图见图8。由图中可明显区分出3种不同类型信号。图8(a)为敲击信号递归点主要沿45°对角线平行分布，平行线间隔近似相等且基本无孤立点，反应出敲击信号的准周期特性。图8(b)为砂纸信号的递归点总体平行主对角线分布，水平空白间距不明显，说明该信号各特征参数变化较缓慢，但在300点附近隐约出现十字带，此分块交替变化说明砂纸信号在该处有轻微的阶段性突变。图8(c)中断铅信号递归点被一条明显十字带分为4块

图8　不同类型信号递归图Fig.8 Different kinds of recurrence plot

区域，在带附近断铅信号发生明显突变。每个小区域中仍存在沿主对角线平行分布的递归点。

通过研究不同类型信号的递归图结构分布，可直观区分模拟声发射信号，实现对其RQA定性分析。计算的定量递归特征参数，结果见表1。其中类别1为敲击信号，2为砂纸信号，3为断线信号。统计3类信号主要递归定量特征参数平均值见表2。由表2看出，不同类别信号平均重标距离、垂直线段均值、熵及趋势参数值存在明显差异，而递归率、确定率及层流率则类别1、3数值相近并略大于2，类别2、3最大线长相似且明显大于类别1最大线长平均值，3类信号熵值存在差异，但差别不大。

不同类别信号在不同递归定量参数值上或多或少存在差异，为SVM分类提供可能。

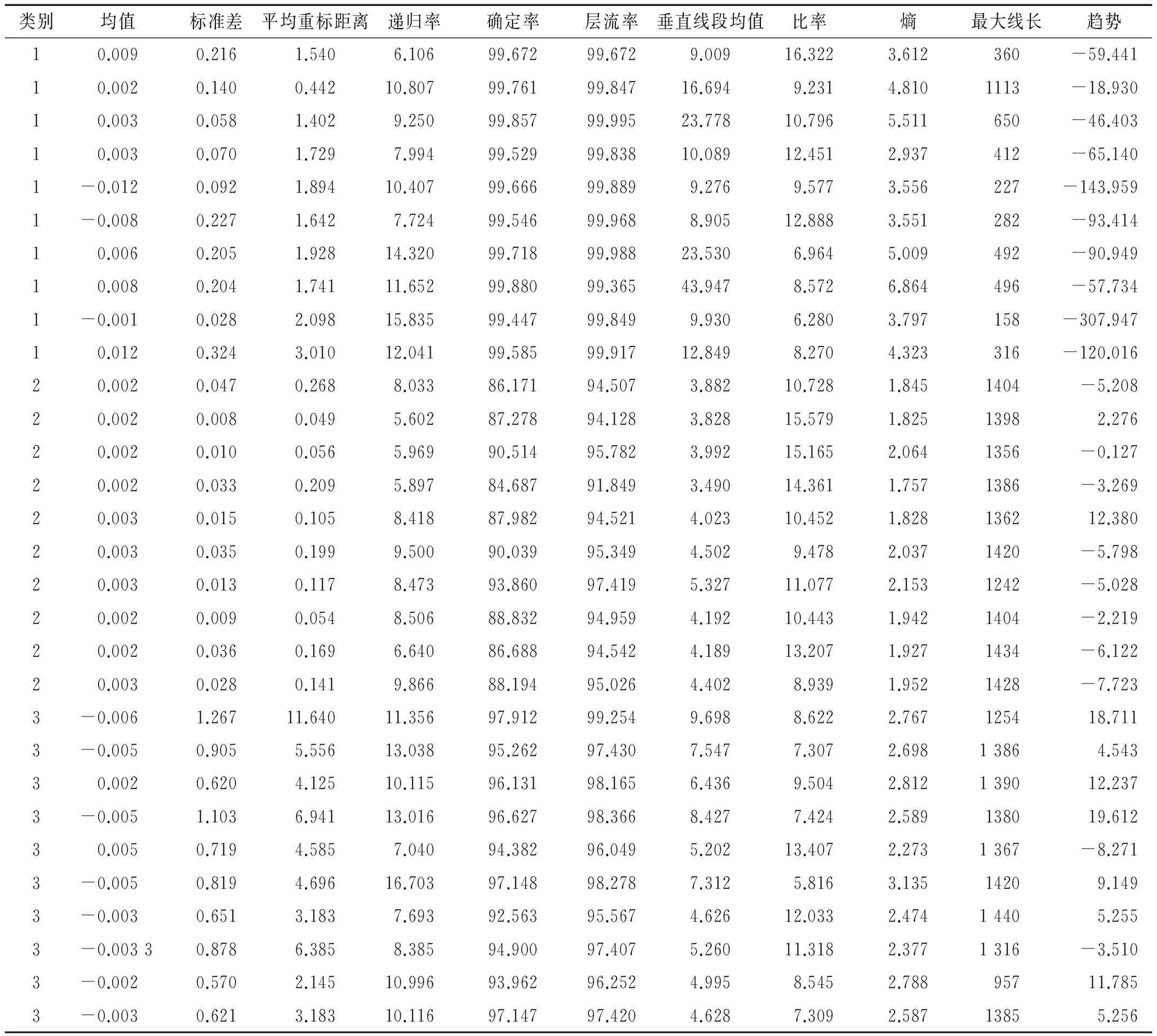
表1　递归定量分析参数

表2　主要递归定量参数均值统计

每类样本取7组作为训练样本，其余3组为测试样本。训练分类器时选核函数类型为高斯径向基核函数，即K(xi,xj)=exp(-γ‖xi-xj‖2)，γ=0.02，惩罚因子C=2。选表1中均值、标准差、平均重标距离、递归率、确定率、层流率、垂直线段均值、比率、熵9个特征参数作为SVM输入训练参数时，对训练样本可视化见图9。此时，9组测试样本仅一组分类错误，分类精度为88.89%。

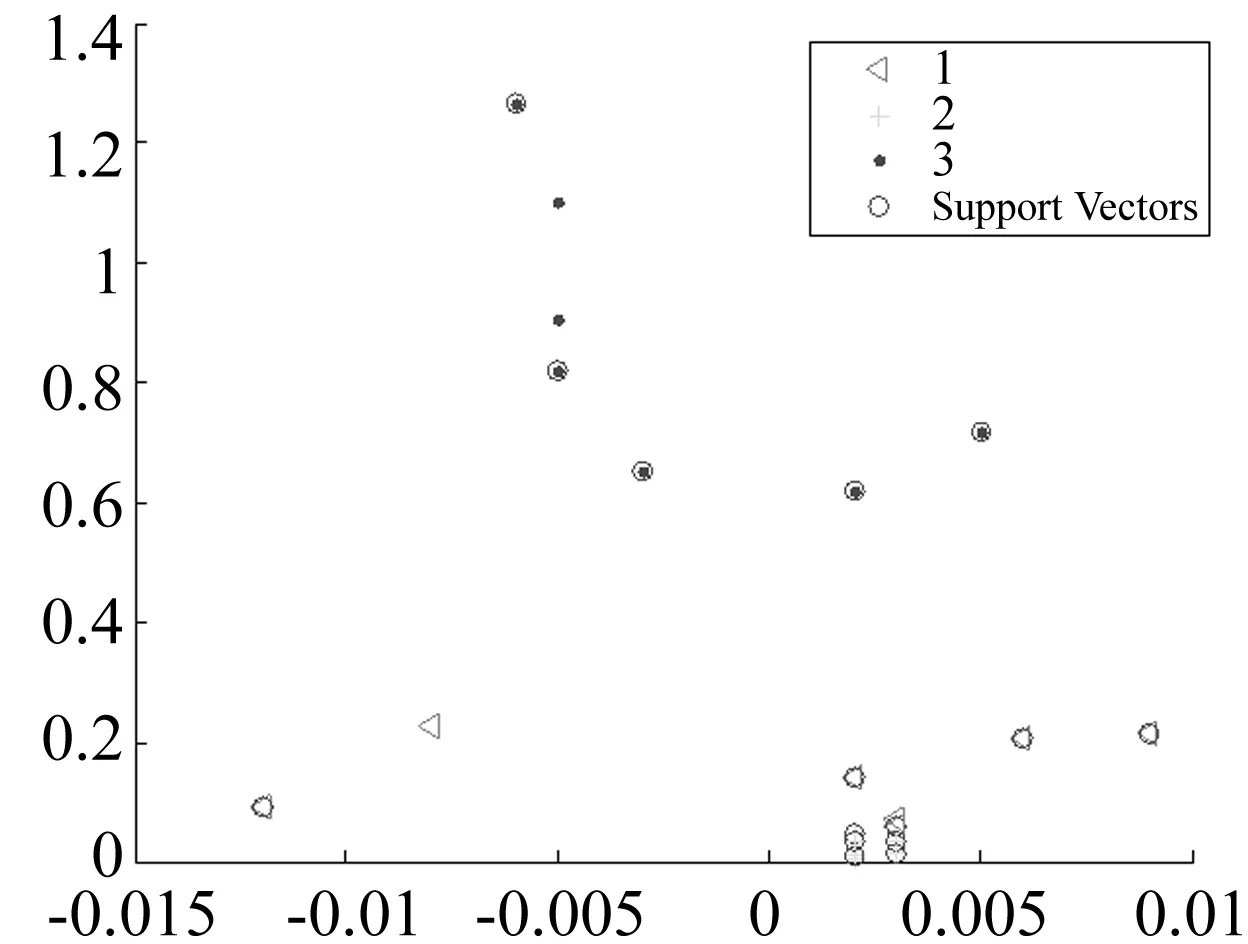
图9　输入特征参数为9个的训练样本Fig.9 Training sample with 9 feature parameters

在分类基础上增加趋势作为第10个输入特征参数后重新训练分类模型，训练样本见图10。可见所得9组测试样本全部分类正确，分类精度100%。

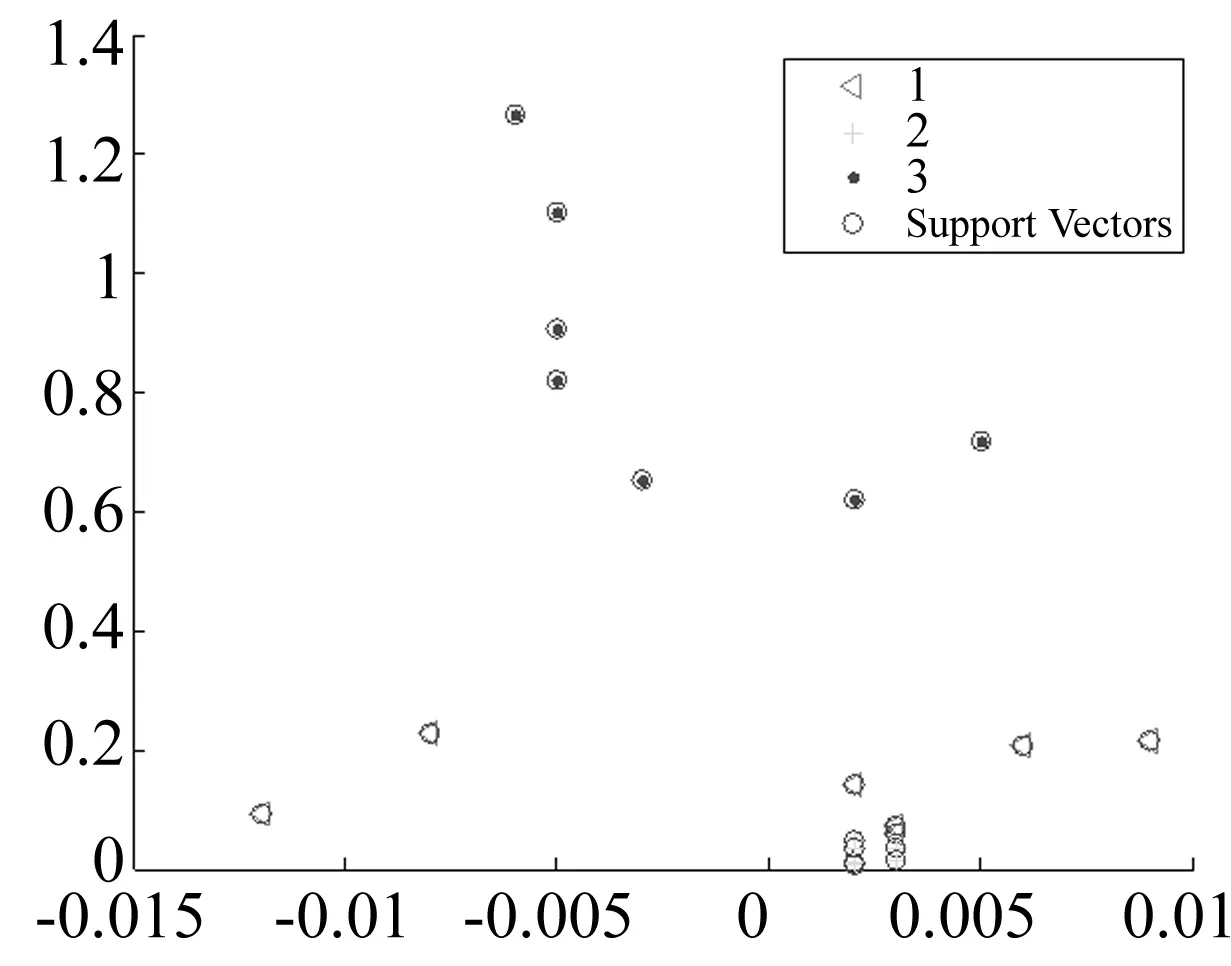
图10　输入特征参数为10个的训练样本Fig.10 Training sample with 10 feature parameters

实验证明，SVM可有效解决样本不足的分类问题，且选合适的定量递归分析参数作为支持向量机输入参数，可有效对3种不同类别声源信号进行识别。为泄漏声发射信号在强背景噪声下识别提供可能。

5.3算法比较

为进一步验证该算法的有效性，现选用EMD结合AR建模提取声发射信号的特征参数，分别用BP神经网络和SVM分类器对其进行分类。其中，选取信号EMD分解得到的5个IMF分量，每个IMF取通过AR模型提取5个特征值，因此，每个信号的特征参数为25个。BP神经网络采用3层神经网络结构，输入层、隐含层和输出层分别含有25、51和3个节点；隐含层和输出层传递函数分别选用S型正切函数(tansig)和S型对数函数(logsig)；学习函数选用tranlm。由于算法需要，现将声发射信号的样本总数由之前的30组增至90组，并且两种分类方法均采用样本总数的2/3作为训练集，剩余的1/3作为测试集。三类算法的分类精度结果如表3所示。

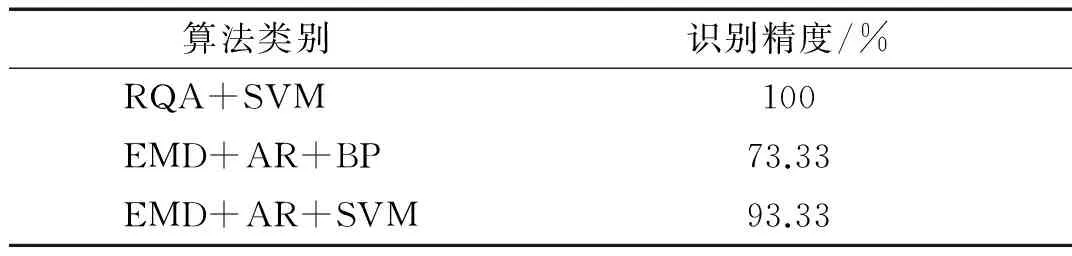
表3　三类算法精度结果

6结论

(1) 通过将递归图、定量递归分析引入声发射信号分析检测，可定性、定量对声发射信号进行直观全面描述。

(2) 支持向量机可有效解决小样本、非线性分类问题，选择合适的定量递归参数训练SVM分类器，可获得准确率较高的分类结果。

参 考 文 献

[1] 林丽.船舶与海洋结构物设计制造[D].大连:大连理工大学,2008.

[2] 王朝晖,张来斌,辛若佳,等.声发射技术在管道泄漏检测中的应用[J].中国石油大学学报:自然科学版,2007,31(5):87-88.

WANG Chao-hui, ZHANG Lai-bin,XIN Ruo-jia, et al. Application of acoustic emission technique in pipeline leakage detection[J]. Journal of China University of Petroleum:Edition of Natural Science,2007,31(5):87-88.

[3] 付俊涛,李玉星,孟令雅,等.输气管道泄漏音波与干扰信号特征提取[J]. 石油化工高等学校学报,2012,25(2):53-54.

FU Jun-tao, LI Yu-xing, MENG Ling-ya,et al. Characteristic extraction of acoustic leak signals and interfering signals for natural gas pipeline[J]. Journal of Petrochemical Universities, 2012, 25 (2):53-54.

[4] 沈继忱,王春雨,王慧丽. 管道泄漏诊断方法研究[J]. 化工自动化及仪表,2012,39(3):309-311.

SHEN Ji-chen, WANG Chun-yu, WANG Hui-li. Method research for pipeline leakage diagnosis[J]. Control and Instruments in Chemical Industry,2012,39(3):309-311.

[5] 林丽,赵德有.局域波神经网络海洋平台AE信号识别研究[J]. 哈尔滨工程大学学报,2008,29(7):663-667.

LIN Li. ZHAO De-you. Identification of acoustic emission signals of offshore structures with both local wave method and neural network[J]. Journal of Harbin Engineering University, 2008,29(7):663-667.

[6] 毛汉颖, 毛汉领,周洁,等.基于BP神经网络的混流式水轮机裂纹声发射源定位方法[J].无损检测,2008,30(7):426-429.

MAO Han-ying, MAO Han-ling, ZHOU Jie, et al. Acoustic emission source location for the crack of francis turbine runner based on BP neural network[J].Nondestructive Testing, 2008,29(7):663-667.

[ 7] 张晓涛,唐立伟,王平,等.基于SVD与Fast Kurtogram算法的滚动轴承声发射故障诊断[J].振动与冲击,2014,33(10):101-105.

ZHANG Xiao-tao, TANG Li-wei, WANG Ping, et al. Acoustic emission fault diagnosis of rolling bearings based SVD and Fast Kurtogram algorithm[J]. Journal of Vibration and Shock,2014,33(10):101-105.

[8] 毛汉领,王向红,黄振峰. 基于小波包分析的声发射信号界面的衰减研究[J].振动与冲击,2008,27(9):139-141.

MAO Han-ling, WANG Xiang-hong, HUANG Zhen-feng. Attenuation of acoustic emission signals due to discontinuous interface based on wavelet packet analysis[J]. Journal of Vibration and Shock,2008,27(9):139-141.

[9] 王向红,朱昌明,毛汉领, 等. 基于小波神经网络的水轮机叶片裂纹源的定位技术[J].上海交通大学学报,2008,42(8):1301-1309.

WANG Xiang-hong, ZHU Chang-ming,MAO Han-ling, et al. Source location of cracks of turbine blades based on wavelet neural network[J]. Journal of Shanghai Jiaotong University, 2008,42(8):1301-1309.

[10] 王向红,朱昌明,毛汉领, 等. 基于核主成分分析及支持向量机的水轮机叶片裂纹源定位[J].振动与冲击,2010,29(11): 226-229.

WANG Xiang-hong, ZHU Chang-ming, MAO Han-ling, et al. Source location of cracks in a turbine blade based on kernel principal component analysis and support vector machines[J]. Journal of Vibration and Shock,2010,29(11):226-229.

[11] 王向红,胡宏伟,张志勇,等. 微弱裂纹信号的稀疏编码提取[J].振动工程学报,2013,26(3):311-317.

WANG Xiang-hong, HU Hong-wei, ZHANG Zhi-yong,et al. Extraction of weak crack signals by sparse code[J]. Journal of Vibration Engineering,2013,26(3):311-317.

[12] 刘勇.基于泄漏电流递归分析的绝缘子状态检测研究[D].天津:天津大学,2009.

[13] 闫润强.语音信号动力学特性递归分析[D].上海:上海交通大学,2006.

[14] 高尚.支持向量机及其个人信用评估[M].西安:西安电子科技大学出版社,2013.

[15] 柯慧,顾洁.电能质量信号的小波阈值去噪[J]. 电力系统及其自动化学报,2010,22(2):103-108.

KE Hui, GU Jie. Wavelet threshold de-noising of power system signals[J]. Proceedings of the Chinese Society of Universities,2010,22(2):103-108.

[16] 杨波.基于支持向量机的中学教师评价系统研究[D].长春:东北师范大学,2008.

[17] Chang C C, Lin C J. Libsvm: a library for support vector machines[R]. Taiwan: Department of Computer Science National Taiwan University,2011.

收稿日期：2014-08-18修改稿收到日期：2014-12-12

通信作者毕贵红 男，博士，教授，1968年生

中图分类号:TB52

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.016

Detection and identification of acoustic emission signals based on recurrence quantification analysis and support vector machines

SI Li1,4, BI Gui-hong2,4, WEI Yong-gang3,4, TAO Ran4, ZHANG Shou-ming1

(1. Faculty of Information Engineering and Automation Kunming University of Science and Technology, Kunming 650500, China；2. Faculty of Electrical Engineering Kunming University of Science and Technology, Kunming 650500, China；3. Faculty of metallurgy and energy engineering Kunming University of Science and Technology, Kunming 650093, China；4. Yunnan Special Equipment Inspection and Research Engineering Center, Kunming 650050, China)

Abstract:To prevent the leakage accidents of pipes and boiler, the key technique lies in whether the signals of cracks and small leaks can be detected effectively. Aiming at this, a new method of detecting acoustic emission signals based on RQA and SVM was described. The theory of wavelet threshold de-noising was used to reduce the noise signal. The principle of RQA was borrowed to detect acoustic emission signals and by calculation, some quantifiable feature parameters were obtained. Using these parameters as the SVM input parameters, the simulated acoustic emission signals of cracks were identified. By experiments, the feasibility of the method was validated.

Key words:acoustic emission; wavelet threshold de-noising; recurrence quantification analysis (RQA); support vector machine (SVM)

第一作者 司莉 女，硕士生，1990年3月生