基于小波奇异谱及SVDD的轴承故障检测方法
2016-07-25李勇发左小清杨芳徐晶
李勇发,左小清,杨芳,徐晶
(1.昆明理工大学 国土资源工程学院,昆明 650093;2.黑龙江科技大学 理学院,哈尔滨 150027)
利用信号处理技术对滚动轴承进行故障检测主要涉及2个问题:1)提取故障信号的特征值,实现降维和去噪的目的;2)利用训练得到的模型进行故障检测[1-2]。故障数据缺乏是故障检测的一大难题,因难以获取样本数据而导致传统的检测方法效果不理想。
支持向量数据描述(Support Vector Data Des-cription,SVDD)具有训练速度快、普适性强等优点,而且在分类过程中仅需一类样本,能够有效处理小样本数据[2-3]。但SVDD算法需要对二次规划问题进行求解,求解过程中的计算量与数据维数成正比,数据维数越高,就需要越多的样本数去准确描述目标类[3]。因此,尝试利用小波分析方法分解初始信号,计算小波奇异谱值并进行优选,实现信号的降维和去噪,然后再使用SVDD进行故障诊断,以取得更好的分类效果。
1 故障诊断流程
1.1 小波奇异值优选
在限定时间序列长度为N=2J的条件下,由信号J个尺度的分解构成的(J+1)×N矩阵为D(J+1)×N,其中:DJ表示信号在j(j=1,2,…,J)尺度下的小波分解细节,SJ表示信号J层小波分解的尺度。
利用小波变换得到下列矩阵
(1)
首先利用小波变换对信号进行分解并计算出奇异谱值,然后以该奇异谱值作为特征进行故障检测[2]。为了提高SVDD算法的分类效果,需对奇异值进行优选。获得的数据不同,奇异值优选的方法也不同,如果拥有部分故障数据,应当选择最适合故障检测的奇异值;如果没有故障数据,则首先假定一个阈值K,将序号小于这个阈值的奇异值作为特征值。
1.2 支持向量数据描述
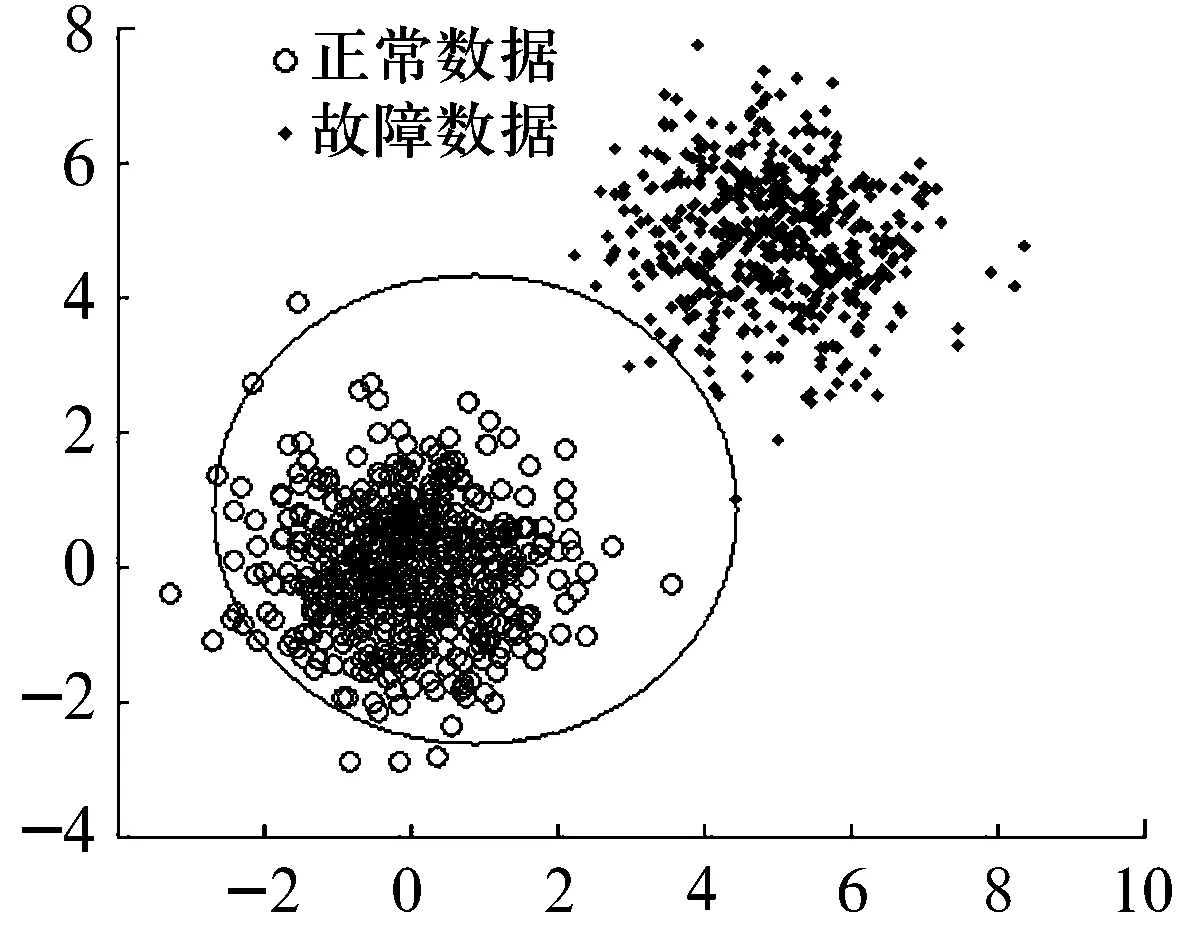
SVDD是一种单值分类方法,其理论基础源于支持向量机[6],但在构建最优超平面上与有监督的支持向量机不同。SVDD算法构建一个最优超球体将目标类数据(球内)与非目标类数据(球外)区分开,对于输入空间不可分时,可引入核函数将其转化为线性可分,然后再构造最优超球体,并使其半径最小且包含大多数据点。该超球体就是区分目标类与非目标类的描述模型,如图1所示。

图1 超球体示意图
对于给定的含有N个数据的训练样本集{xi,i=1,2,…,N},构造中心为a和半径为R的超球体,定义结构风险ε=(R,a)=R2,限制条件为xi-a≤R2,引入松弛因子ξi和惩罚参数C,对初始函数进行最小化,即
(2)
s.txi-a2≤R2+ξi,
ξi≥0(i=1,2,…,N)。
引入Lagrange乘子进行化简后得
(3)
对Lagrange函数求关于R,a,ξi的偏导数,并令其等于0得
。(4)
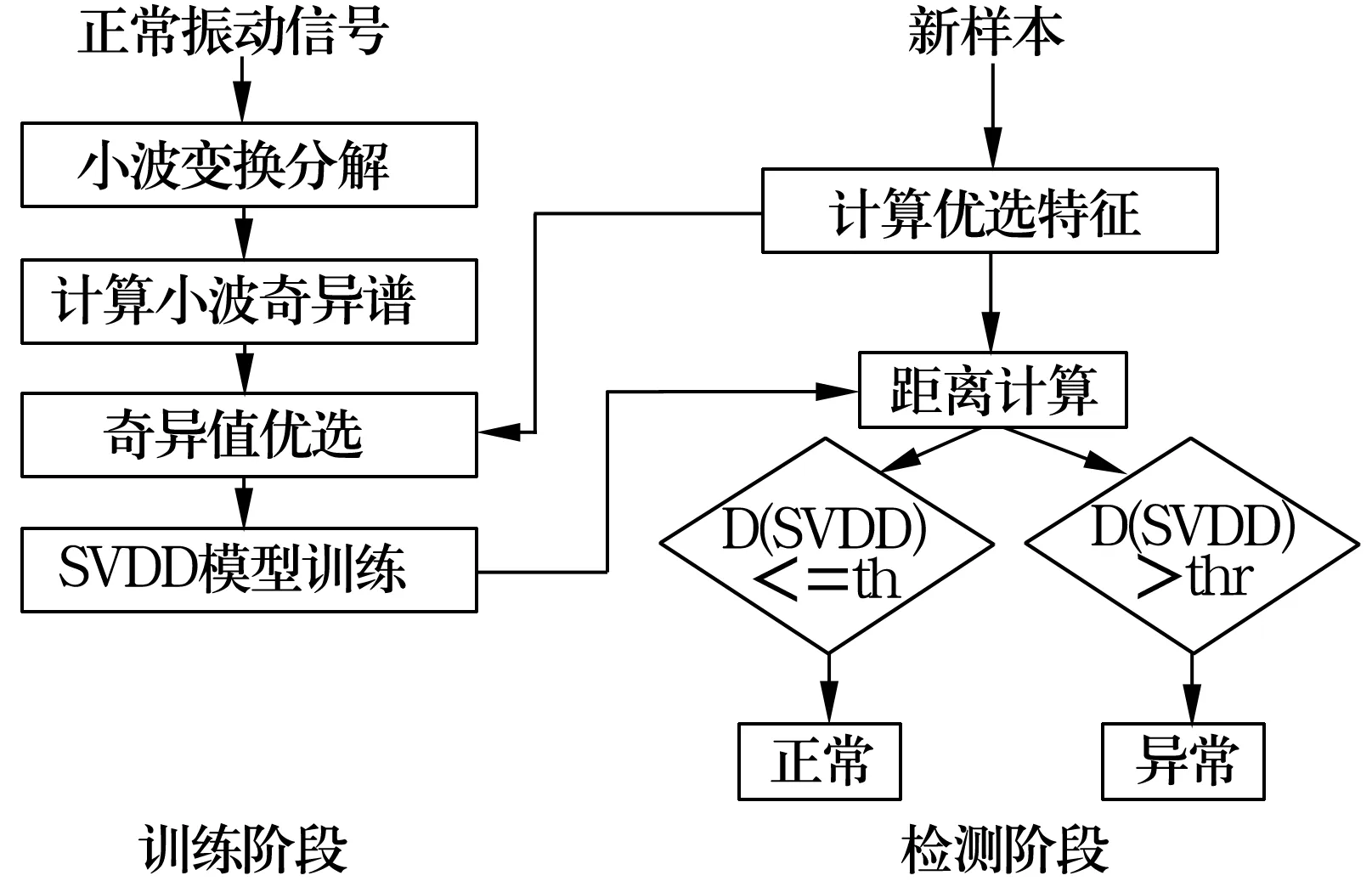
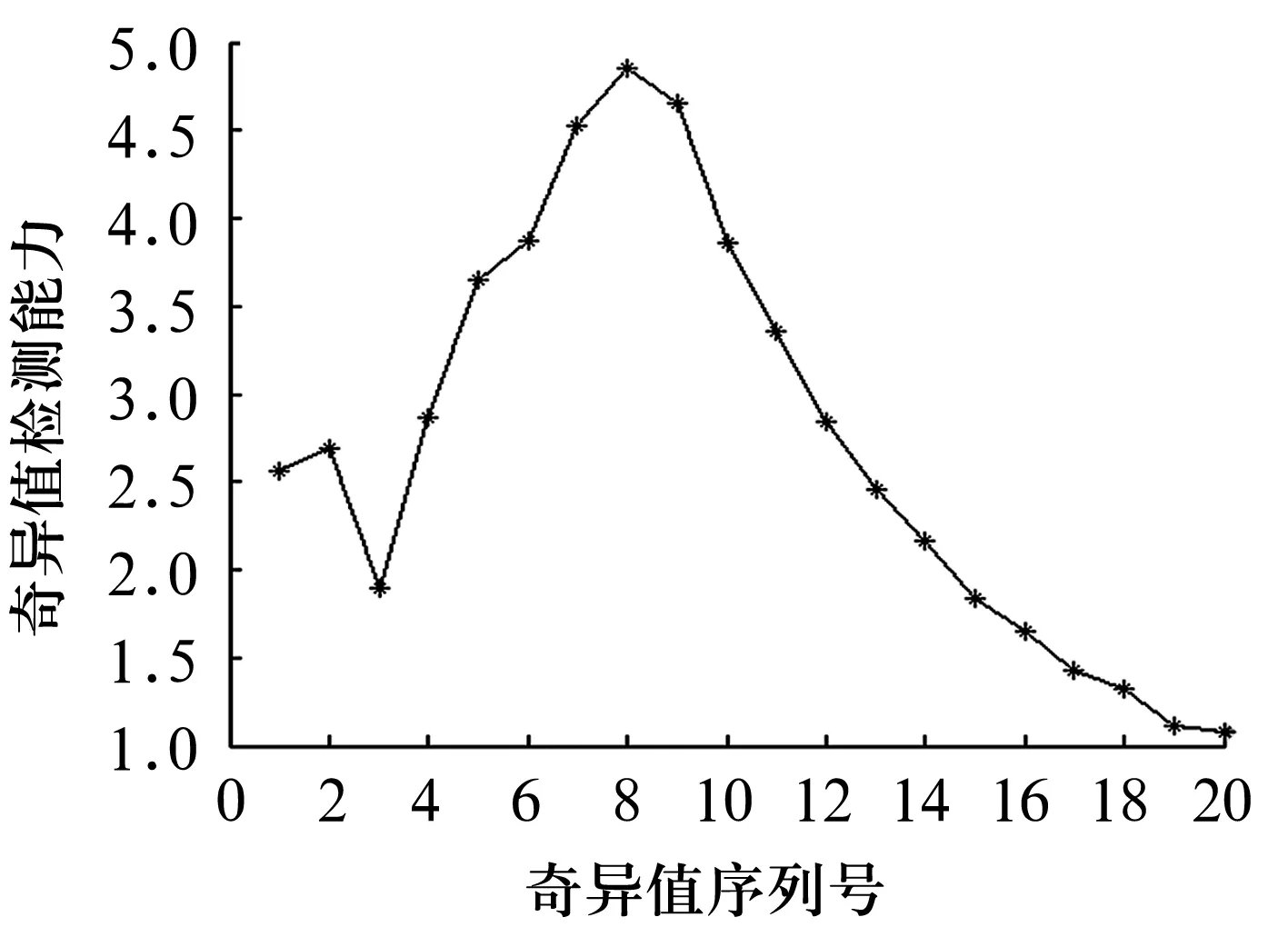
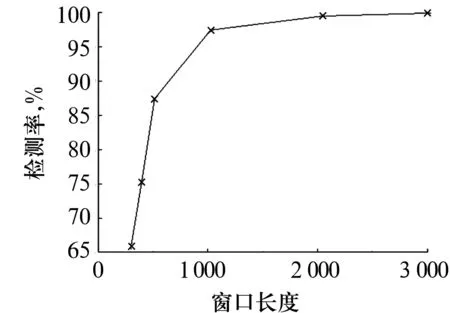
求出当L达到最小值时的αi。当αi=0时对应的样本点xi为内部点,即目标样本点;αi=C时对应的xi为外部点,即非目标点;0≤αi 。(5) 对于某一待测样本Z,可用决策函数划分其所属类别,即 fSVDD(z,a,R)=(z-a)(z-a)T= (6) (7) 式中:Q为指示函数。若Q为真,则标记为-1,说明是目标类样本;反之标记为1,说明是非目标类样本。 检验一组新样本数据的决策函数为 (8) 从上述分析可知,SVDD模型只需通过训练得到球体中心a和球体半径R,即可构成故障检测模型,用于新样本的识别。 核函数是将输入空间通过非线性函数映射到高维特征空间,可以用原始输入空间中核函数的计算替代高维特征空间内积的计算,从而大大减少计算量[9-10]。选用高斯核函数代替内积,即 (x.y)→K(x,y)=exp(-‖x-y‖2/s2), (9) 则检验一个新数据对象的决策函数变为 首先,利用db5小波对正常振动信号进行5层小波分解,计算出奇异值进行优选;然后,将优选出来的奇异值输入SVDD中进行训练,并利用(5)式计算超球体中心和半径;最后,利用判别函数进行分类(正常或故障),故障检测流程如图2所示。 图2 基于SVDD的故障检测流程 某型号轴承正常状态及内圈、外圈、滚动体发生磨损的故障状态下原始信号的时域波形如图3所示[11]。从图中可以看出,正常状态下振动信号比较平稳,幅值较低;故障信号的幅值较大,其中滚动体振动信号中包含周期性的瞬时冲击成分。 图3 原始信号的时域波形图 每种状态取20组样本,利用db5小波进行分解并计算小波奇异谱值,结果如图4所示。从图中可以看出,利用小波变换得到的奇异值按递减顺序排列,在前10个奇异值特征上,正常样本与内、外圈故障数据的线性区分能力较为明显,但与滚动体之间的线性区分能力不明显。 图4 不同状态下振动信号的奇异谱均值 利用SVDD对前20个奇异值进行线性区分能力因子测试,正常状态与不同故障状态间的线性区分能力如图5所示。结果表明:正常数据与内、外圈故障数据间的线性区分能力随着奇异值序号的增加而降低,与滚动体故障间的线性区分能力则随奇异值序号的增加而逐渐上升。 图5 不同奇异值的线性区分能力 定义线性检测能力为 (16) 式中:p为故障数据;k为正常样本数据;ri为第i个奇异值。不同奇异值维度的线性区分能力如图6所示。 图6 不同奇异值维度的线性区分能力 从图中可以看出,第3个奇异值处线性区分能力较低,第8和第9维奇异值处噪声对线性区分能力影响最强。为使正常信号与滚动体信号之间的区分能力提高,将[8,9,7,6,10,5,11,4,2]9个奇异值维度作为特征向量输入SVDD进行故障检测。 不同窗口大小对检测正确率的影响如图7所示。结果表明:数据窗口越大,检测正确率越高;反之,检测正确率越低。但数据量的加大会加倍的增加计算量,并造成系统延迟,因此应根据实际情况选择窗口大小。从图中可以发现,当窗口大小为1 024时,就已经能够达到较好的效果。 图7 窗口大小对检测性能的影响 高斯核参数对SVDD检测正确率的影响如图8所示。从图中可以看出:高斯核宽度与正常样本的检测正确率成正比,与故障样本的检测正确率成反比。当高斯核宽度为0.3时,正常及故障样本的检测正确率均达到最大。 图8 不同核函数参数对检测率的影响 利用优选得到的9个奇异值作为特征向量输入SVDD分类器进行训练。选择高斯核函数宽度为0.3,构建好SVDD模型后,按 (7) 式求出超球体中心和半径,即可对新样本进行分类。经过训练得R=3.091 912,a=0.418 414。利用测试样本(测试样本数为2 936,其中内圈、外圈、滚动体故障样本数分别为582,586,588)进行模型检验,分类效果如图9所示,检测正确率达到了98.6%。 采用小波分析提取奇异值并进行优选能够有效提取可充分反映故障本质的敏感特征,从而使训练和分类效果得到很大的提高。而通过选择合理的窗口大小及高斯核宽度,SVDD算法的检测正确率达到了98.6%,完全能够满足轴承故障诊断的要求。但上述方法主要检测了有无故障发生,还不能准确判断故障发生部位,需做进一步研究。 图9 SVDD分类效果图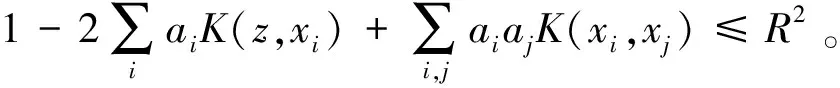
1.3 故障检测流程
2 试验分析

2.1 线性区分能力分析


2.2 基于SVDD的轴承故障检测方法

3 结束语