液压型落地式风力发电机组长管道谐振分析

艾　超，　刘艳娇，　叶壮壮，　孔祥东

(1. 燕山大学 先进锻压成形技术与科学教育部重点实验室， 河北秦皇岛 066004；2. 燕山大学 河北省重型机械流体动力传输与控制实验室， 河北秦皇岛 066004；3. 燕山大学 机械工程学院， 河北秦皇岛 066004)



液压型落地式风力发电机组长管道谐振分析

艾超1,2，刘艳娇3，叶壮壮3，孔祥东1,2

(1. 燕山大学 先进锻压成形技术与科学教育部重点实验室， 河北秦皇岛 066004；2. 燕山大学 河北省重型机械流体动力传输与控制实验室， 河北秦皇岛 066004；3. 燕山大学 机械工程学院， 河北秦皇岛 066004)

摘要：为了探究系统参数对系统谐振的影响，了解具有长管道结构的液压型落地式风力发电机组稳定运行的条件，建立了机组液压主传动系统数学模型，分别从能量输入端、液压元件本身及能量输出端3个方面研究系统谐振激励源，并通过仿真对比研究了系统压力比频率特性影响因素，得出各参数对系统谐振的影响规律.结果表明：管径、管长和油液运动黏度等对系统传输压力比幅值影响较大，油液运动黏度和等效体积弹性模量同样也影响系统的工作频段；系统谐振频率都以基频的奇数倍形式存在.

关键词：液压型落地式; 风力发电机组； 长管道； 谐振激励源； 压力传输

液压型风力发电机组因利用无污染且分布广泛的风能作为输入能源，并且具有机舱重量小、适用范围广的优势，逐渐成为各国推崇的绿色能源应用技术，相应的控制技术也成为一个新的研究方向[1-2].为进一步适应发电要求，出现了一种新机型即液压型落地式风力发电机组，该机组通过将变量马达、发电机等设备落地安装以减少机舱重量，增加了安装维护的可操作性，也更符合工程推广的应用要求，因此成为新的研究热点.而落地式安装带来的长管道结构降低了系统刚度，增大了谐振风险，综合发电过程中对系统稳定性的要求，谐振分析就成了风力发电研究过程中不可回避的问题.

鉴于液压型落地式风力发电机组在工程应用中的实际优势以及长管道结构带来的弊端，国内外学者相继开展了管道结构对系统动态特性及稳定性影响的研究.Xie等[3]认为管长是对管道系统固有频率影响最显著的因子；朱勇等[4]针对阀控系统阐述了管长与管径对系统动态稳定性的影响规律；姚静等[5]对锻造液压机管道进行了研究，得出管径和管长影响系统波动的结论；葛振亮等[6]研究了液压管道参数对转向系统动态特性的影响；Bae等[7]研究分析了换向阀与液压泵之间的管长在系统产生谐振中所起的作用；Mikota[8]建立了管道比例阻尼等效力学模型，反映了结构阻尼反共振的优势；Malekzadeh等[9]实验研究了立管管道的压力流量波动问题等；Gorin等[10]提出通过减小振动源的流量压力脉动来减小管路振动、调整管道系统阻抗，并调整系统的谐振点避开振动源流量和压力脉动的主频率，避免发生谐振.以上研究都在一定程度上揭示了长管道结构对系统性能的影响，但研究多集中于阀控系统管道结构参数对系统特性及稳定性的影响，而在带长管道结构的泵控系统中，对系统干扰激励的分析以及系统主要参数对谐振影响规律的研究鲜见报道.

笔者以带长管道的液压型落地式风力发电机组(以下简称机组)为研究对象，在建立机组主传动系统数学模型的基础上，针对系统谐振问题，探究系统输入输出端的谐振激励源，并进一步研究系统参数对压力传输特性的影响规律.

1机组主传动系统结构特性

液压型落地式风力发电机组机舱内的定量泵与塔基处的变量马达通过长管道结构构成闭式回路，传递液压能以驱动发电机发电.图1为该机组系统结构简图.长管道结构中，当定量泵出口端即管道入口端压力波动、变量马达元件压力波动及马达端发电机电磁转矩波动时，所产生的激励都会影响液压传动系统的能量传递，使系统在很多频率点处产生谐振.因此，在机组运行发电过程中，如何避免谐振的发生对系统稳定发电具有重要意义.

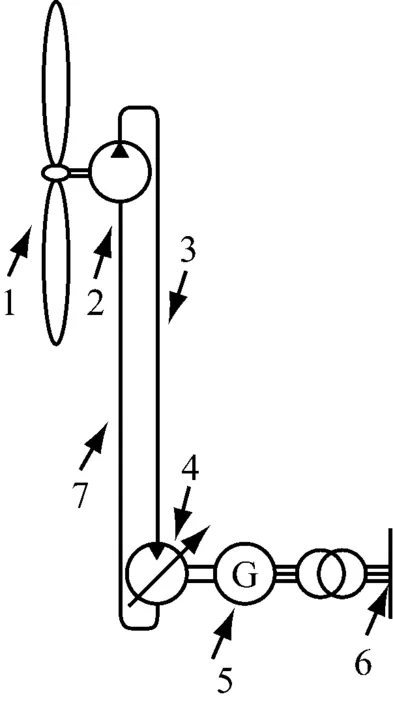
1-风轮机； 2-定量泵； 3-高压长管道； 4-变量马达； 5-发电机； 6-电网； 7-低压长管道.

图1液压型落地式风力发电机组系统结构简图

Fig.1Schematic diagram of the hydraulic-driven floor-type wind

turbine system

2机组主传动系统数学模型

液压型落地式风力发电机组主传动系统原理图见图2.

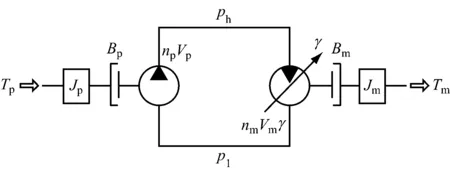
图2　主传动系统原理图

2.1定量泵模型

定量泵的体积流量方程为

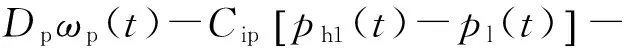
(1)

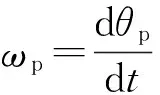
式(1)增量方程的拉氏变换为

(2)

式中：Ctp为定量泵总泄漏系数，Ctp=Cip+Cep，m3/(s·Pa).

定量泵力矩平衡方程为

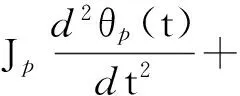
(3)

式中：Tv为风轮旋转力矩，N·m；Jp为风轮与定量泵折合的转动惯量，kg·m2；Bp为定量泵的阻尼系数，N·m·s / rad；Gp为泵端弹簧刚度，N·m/rad.

式(3)进行拉氏变换后可得：

(4)

2.2变量马达模型

变量马达的体积流量方程为

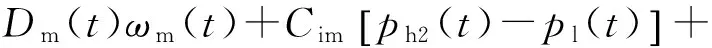
(5)

式中：qV,m为变量马达体积流量，m3/s；Dm为变量马达排量，Dm=Kmγ，m3/rad，其中Km为变量马达排量梯度，m3/rad，γ为变量马达摆角，取值为[0,1]；ωm为变量马达转速，rad/s；Cim为变量马达内泄漏系数，m3/(s·Pa)；Cem为变量马达外泄漏系数，m3/(s·Pa)；ph2为变量马达入口高压管路压力，Pa；Vm为变量马达的高压腔容积，m3.

变量马达力矩平衡方程为

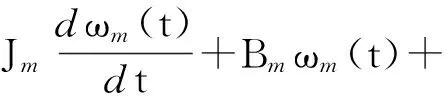
Gmθm(t)+Tm(t)

(6)

式中：Jm为变量马达轴上的总转动惯量，kg·m2；Bm为黏性阻尼系数，N·m·s/rad；Gm为负载弹簧刚度，N·m/rad；θm为变量马达转角，rad；Tm为作用在变量马达上的负载转矩(电磁转矩)，N·m.

由于变量γ与ph2的乘积具有非线性，进行线性化[11]处理后，忽略二阶无穷小量，整理得：

(7)

式中：γ0为变量马达初始摆角；ph20为变量马达入口高压管路初始压力，Pa；Δγ为变量马达摆角变化值；Δph2为变量马达入口高压管路压力变化值，Pa.

将式(7)代入变量马达力矩平衡方程，并取增量方程的拉氏变换：

Kmγ(s)ph20+Kmγ0Ph2(s)=Jmsωm(s)+Bmωm(s)+

Gmθm(s)+Tm(s)

(8)

同理，体积流量方程的拉氏变换为

QV,m(s)=Kmγ(s)ωm0+Kmγ0ωm(s)+

(9)

式中：Ctm为变量马达总泄漏系数，Ctm=Cim+Cem,m3/(s·Pa)；ωm0为变量马达初始转速，rad/s.

2.3液压长管道模型

基于线性磨擦理论，管道分布参数模型如图3所示，图中R、C、L和G分别代表每单位长度的液阻、液容、液感和液导[12].

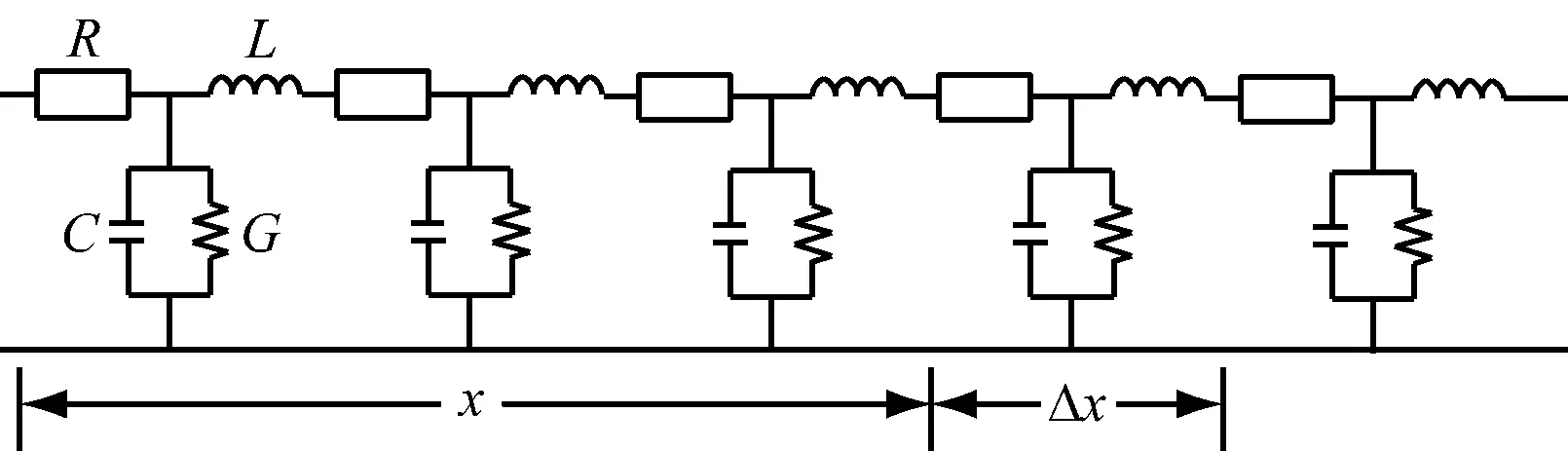
图3　管道分布参数模型简图

设定q(x,t)和p(x,t)分别为管道上任一点的瞬时流量和压力，x为管长，Δx为管长变化量，根据基尔霍夫定律有：

(10)

长度为l的管道，其边界条件为：x=0，P(x,s)=Pin(s)，Q(x,s)=QV1(s)；x=l，P(x,s)=Pout(s)，Q(x,s)=QV2(s).解得:

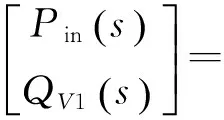
(11)

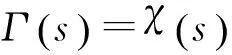
可以看出管道的频率特性主要取决于串联阻抗和并联导纳2个参数.采用线性摩擦理论，管道串联阻抗和并联导纳[10]的计算式为

(12)

(13)

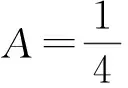
3液压长管道闭式系统的谐振分析

基于线性摩擦理论管道模型，对液压型落地式风力发电机组管道系统在频域内的压力传递特性进行研究.

3.1输入端对系统特性的影响

系统的能量输入端是引起系统谐振、失稳等情况的主要激励，液压型落地式风力发电机组中，风力机便是其能量输入端.风力机与柱塞泵固联，自然风驱动风力机以带动柱塞泵转动，因此机组的输入端波动激励可分为2类：(1) 定量泵驱动端，来自风力机的波动转矩，体现在低频段；(2) 由定量泵特性本身所带来的附加波动激励(流量波动等).这2类波动激励最终反映到液压系统上，便是定量泵输出端流量与压力的波动.

3.1.1定量泵驱动端对系统的影响

对于定量泵，联立式(2)与式(4)可得：

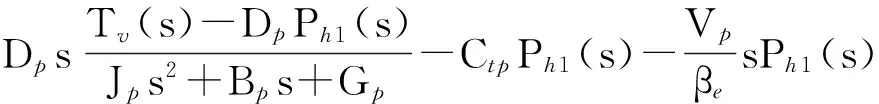
(14)

由流体传输管道动态特性基本方程式(11)变形可得：

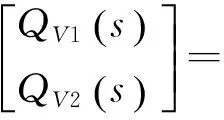
(15)

管道入口端压力Pin也即定量泵出口高压管路压力Ph1，管道出口端压力Pout也即变量马达入口高压管路压力Ph2.联立式(14)与式(15)可得：

(16)

从式(16)可以看出，管道入口端压力Pin与风轮旋转力矩Tv以及管道出口端压力Pout有关.风轮旋转力矩作为系统的输入经过定量泵转换为压力能，最直接的表现是与定量泵端的压力能相互作用，直至达到平衡，由式(16)可得Pin对Tv的传递函数：

(17)

令Gp=0，式(17)可简化为

(18)

由式(18)可得，定量泵端风轮与定量泵折合的转动惯量、管道参数、油液等效体积弹性模量和定量泵的排量等都会影响传递函数.基于式(18)，以所研究对象的实验系统参数作为仿真参数进行仿真研究，系统参数见表1.

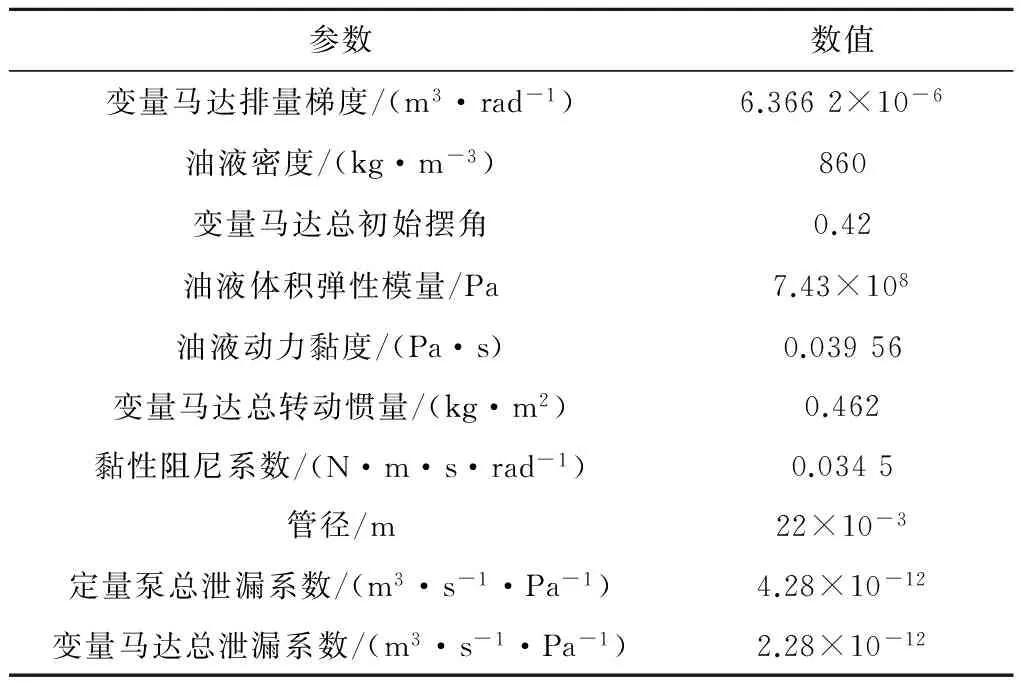
表1　系统参数

取10 m管长，得到300 Hz内定量泵出口高压管路压力对输入转矩的幅值比(见图4).由图4可知，谐振频率呈奇数倍增加，若定量泵轴端驱动力矩的波动频率落在以上谐振点处，可能会对系统带来有害的影响；而随着谐振频率的增加，谐振幅值减小，当谐振频率达到208 Hz时，幅值比较小，可以忽略其影响.

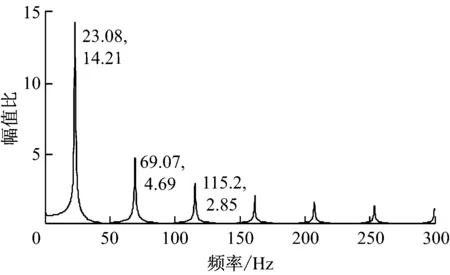
图4　300 Hz内定量泵出口高压管路压力对输入转矩的幅值比特性图

3.1.2定量泵元件对系统谐振的影响

定量泵元件对系统谐振的影响与定量泵本身有关，对于本文采用的柱塞泵，其输出的脉动频率为

(19)

式中：ωbp为柱塞泵输出脉动频率，rad/s；n柱塞p为柱塞泵内柱塞的个数；np为柱塞泵的转速，r/min.

当脉动频率ωbp落入系统谐振频带内时，将对系统产生严重影响，此时需要避免系统可能发生谐振的工况.

3.2输出端对系统特性的影响

机组的另一组激励来自能量输出端，包含了变量马达端电磁转矩的变化给系统带来的影响以及变量马达元件本身带来的流量波动.其中变量马达端电磁转矩主要影响系统的高频段.

3.2.1变量马达端电磁转矩对系统的影响

对于变量马达，联立式(8)和式(9)，Gm=0 (负载恒定)，增量方程的拉氏变换为

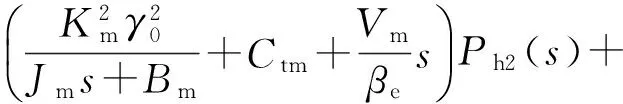
(20)

(21)

从式(21)可以看出，影响管道出口端压力Pout的参数有管道入口端压力Pin、变量马达摆角γ和负载转矩Tm.由式(21)可得：

(22)

(23)

对以上传递函数进行频谱分析可得，波峰处的频率值是一样的，只是幅值比会有所不同.

3.2.2变量马达元件对系统谐振的影响

变量马达元件对系统谐振的影响与其本身有关，对于所采用的柱塞式变量马达，其输出的脉动频率为

(24)

式中：ωbm为柱塞式变量马达的输出脉动频率，rad/s；n柱塞m为柱塞式变量马达内柱塞个数；nm为柱塞式变量马达转速，r/min.

与定量泵一样，此时需要避免系统可能发生谐振的工况.

3.3压力比频率特性影响因素研究

管道的压力比频率特性反映了管道输出端压力与输入端压力在频域内的传递特性.在实际系统中，压力值的检测相对方便，故研究管道的压力比频率特性以分析管道的谐振情况具有重要的工程意义.

(25)

(26)

则式(22)可写成

(27)

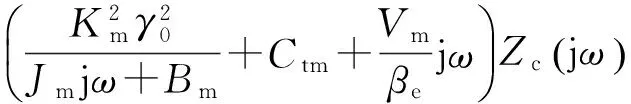
(28)

(29)

因此，管长l、管道材料与油液等效体积弹性模量E、管径d、油液动力黏度μ及油液密度ρ直接影响着系统的谐振频率.

为了更明确地研究各个参数对压力比频率特性的影响，定义标准参数：l标=3 m，d标=22 mm，βe标=7.43×108Pa，ν标=46×10-6m2/s.并采用Matlab进行编程计算.

3.3.1管长对系统压力传输特性的影响

在保持其他参数不变的情况下，分别设定管长l为标准管长l标的1倍、2倍、3倍和4倍，计算得到300 Hz频率范围内的压力比幅值(见图5).

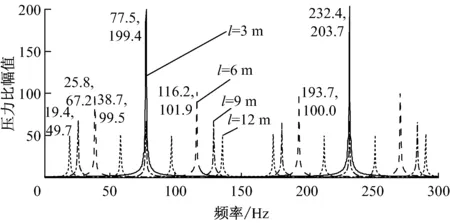
图5　不同管长下的系统传输压力比幅值

由图5可知，当管长一定时，谐振点的频率为一阶谐振频率的奇数倍；随着管长的增加，系统工作频段越来越窄，谐振点数目越来越多.此外，谐振点处的压力比幅值也呈下降趋势，这是因为随着管长的增加，压力波传播时与管道壁的碰撞次数增加，加速了压力比幅值的衰减.

3.3.2管径对系统压力传输特性的影响

在保持其他参数不变的情况下，设定管径d分别为16 mm、22 mm和30 mm，得到300 Hz频率范围内的压力比幅值特性图(见图6).其中图6(b)为一阶谐振点的局部放大图.

从图6可以看出，随着管径的增大，谐振频率并没有变化，但压力比幅值会明显升高，这是因为随着管径的增大，压力波在管道中传播时与管壁碰撞次数减少，从而使得耗散比较慢.

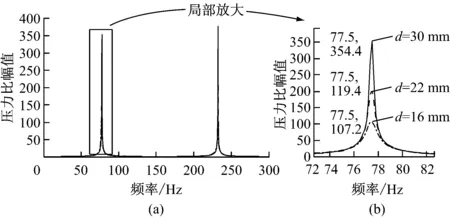
图6　不同管径下的系统传输压力比幅值

3.3.3油液运动黏度对系统压力传输特性的影响

在保持其他参数不变的情况下，分别设定油液运动黏度ν为标准黏度ν标的0.5倍、1.0倍和1.5倍，得到压力比幅值特性图(见图7).其中图7(b)为一阶谐振点的局部放大图.从图7可以看出，随着油液运动黏度的增大，谐振频率的分布并没有变化，但压力比幅值变化非常明显，呈下降趋势.这是因为随着油液运动黏度的增大，压力波在传递过程中受到的阻力变大，衰减也就较快.

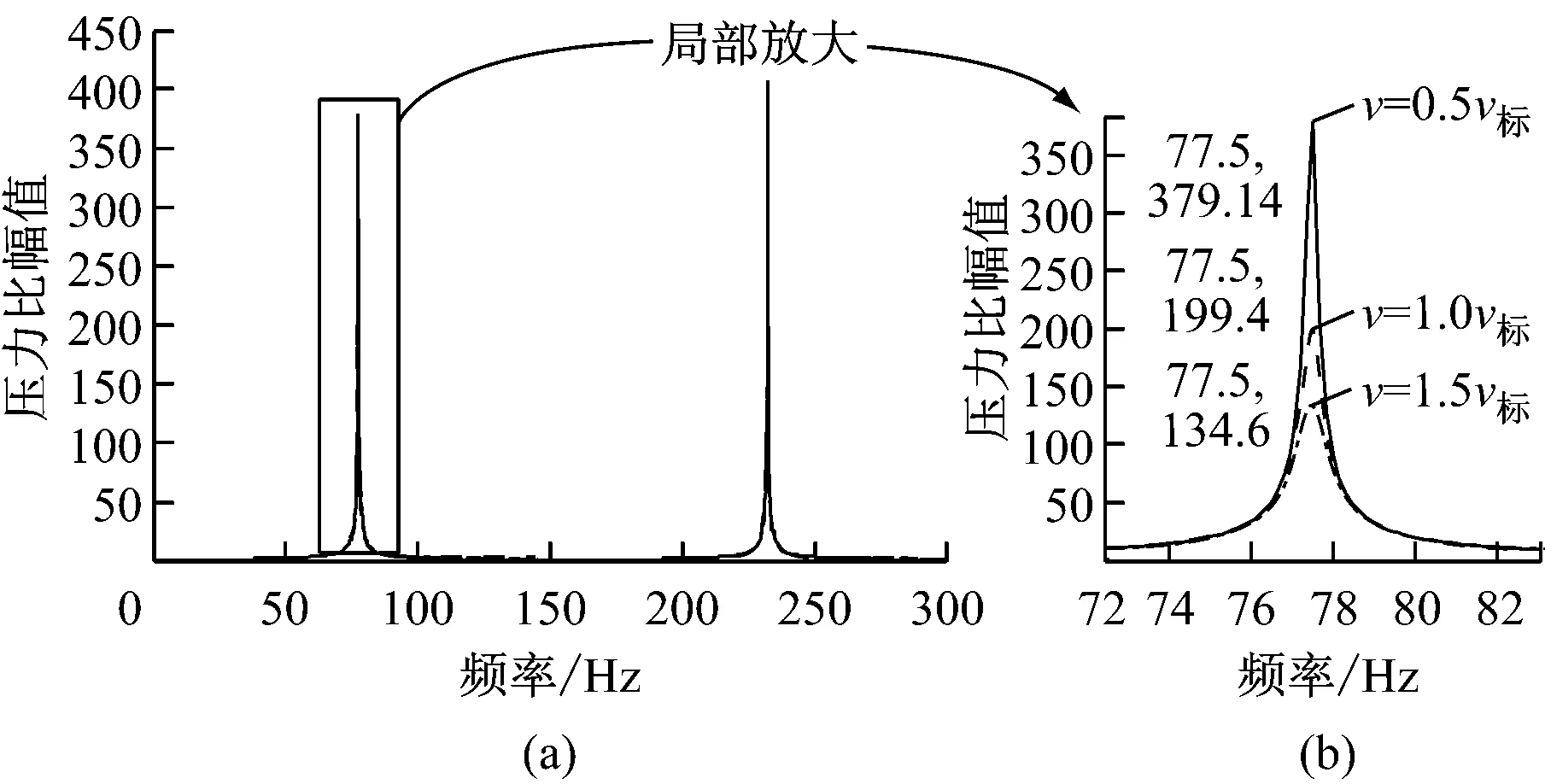
图7　不同油液运动黏度下的系统传输压力比幅值

3.3.4油液等效体积弹性模量对系统压力传输特性的影响

在保持其他参数不变的情况下，分别设定油液等效体积弹性模量βe为标准油液等效体积弹性模量βe标的0.5倍、1.0倍和1.5倍，得到压力比幅值特性图(见图8).

从图8可以看出，随着油液等效体积弹性模量的增大，一阶谐振频率逐渐增大，并且在谐振点处的压力比幅值也随之升高.此时可将油液等效为液压弹簧，其等效体积弹性模量就类似于弹簧刚度，当油液等效体积弹性模量增大时，也就是液压弹簧刚度增大，系统的固有频率会增大，导致谐振点频率增大.

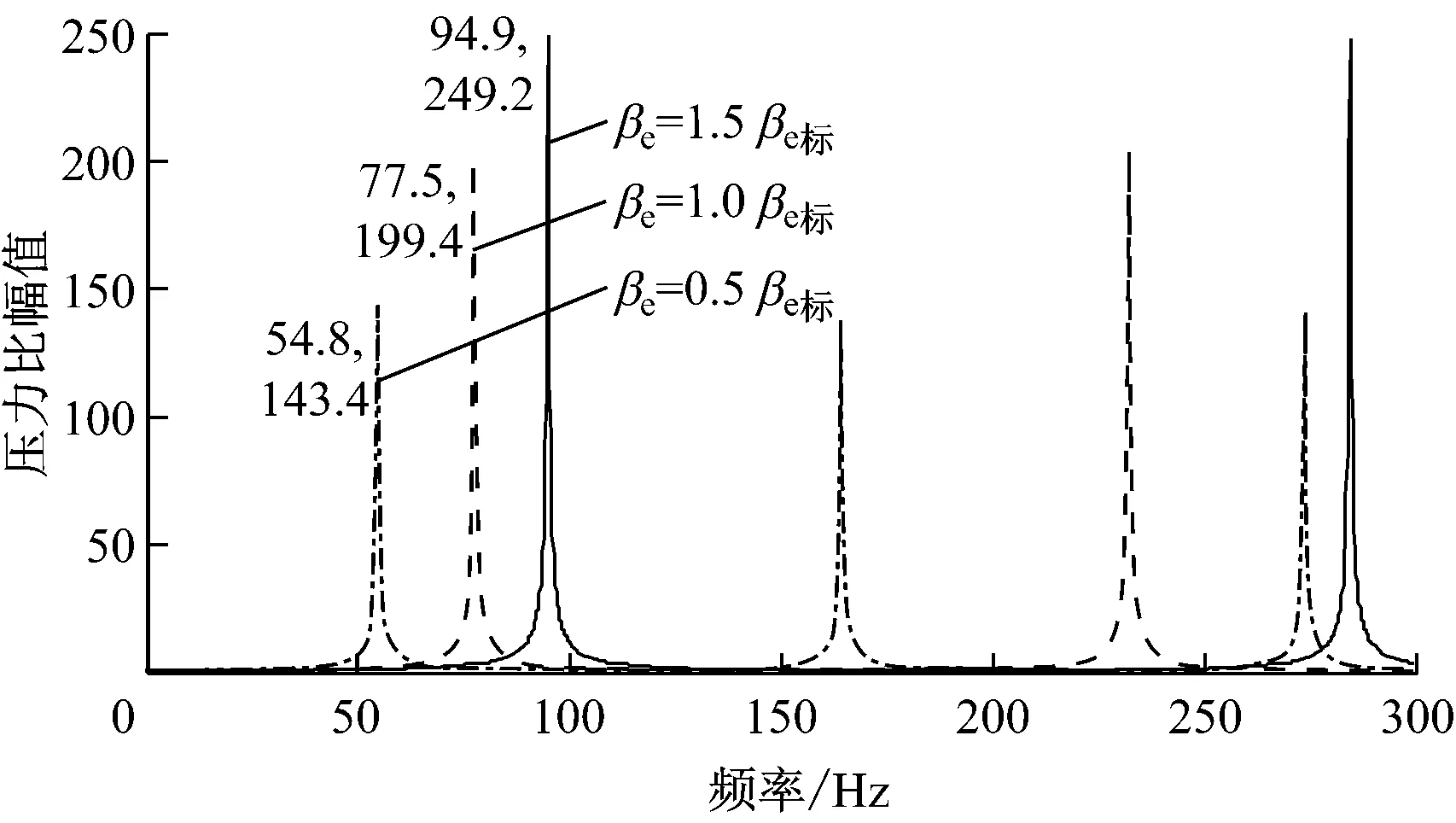
图8　不同油液等效体积弹性模量下的系统传输压力比幅值

4结论

(1) 管径与油液运动黏度对系统谐振的影响主要表现在压力比幅值的变化，管径增大，压力比幅值升高；而油液运动黏度增大，压力比幅值下降.

(2) 管长与油液等效体积弹性模量对系统谐振的影响作用相反，随着管长的增加，压力比幅值下降且工作频段变窄，而油液等效体积弹性模量增大则会使谐振点的压力比幅值升高，工作频段变宽.

(3) 系统谐振的基频与管长的一次方、密度的1/2次方成反比，与管路材料与油液等效体积弹性模量的1/2次方成正比.基频在系统谐振的研究中具有重要作用，谐振频率都以基频的奇数倍形式存在.

参考文献：

[1]艾超，孔祥东，闫桂山，等.液压型风力发电机组最优功率追踪控制方法研究[J].动力工程学报，2015，35(2)：127-133.

AI Chao, KONG Xiangdong, YAN Guishan,etal. Control on maximum power point tracking of hydraulic wind turbines[J].Journal of Chinese Society of Power Engineering,2015,35(2):127-133.

[2]CHAPPLE P, NISS M. A method and system for connecting a wind turbine system to an electric grid: Europe, EP 2481915A1[P].2012-08-01.

[3]XIE Jinghua， TIAN Ke, YANG Dawei. The effect of TBM hydraulic piping system parameters on FSI vibration[C]//Intelligent Robotics and Applications—Third International Conference.Shanghai：Springer Berlin Heidelberg，2010:363-371.

[4]朱勇，姜万录，杨超，等.第二类管道效应对电液伺服系统动态特性影响的研究[J].液压与气动，2013(2)：23-27.

ZHU Yong, JIANG Wanlu, YANG Chao,etal. Dynamic characteristics study of electro-hydraulic servo system impacted by the second pipeline effect[J]. Chinese Hydraulics & Pneumatics,2013(2):23-27.

[5]姚静，孔祥东.锻造液压机管道动态特性仿真研究[J].机床与液压，2011,39(9): 105-107.

YAO Jing, KONG Xiangdong. Study on pipe dynamic characteristics of forging hydraulic press[J].Machine Tool & Hydraulics,2011,39(9): 105-107.

[6]葛振亮，侯友山，姜勇.工程车辆全液压转向系统管路特性分析[J].振动与冲击，2011,30(3): 60-63.

GE Zhenliang, HOU Youshan, JIANG Yong. Dynamic characteristics analysis of hydraulic pipes in fully hydraulic steering system of engineering vehicles[J].Journal of Vibration and Shock,2011, 30(3)：60-63.

[7]BAE C H, GU J R, CHUNG J W.The control of the turbulent vibration of hydraulic oil piping system[C]//18th International Congress on Sound and Vibration 2011 (ICSV 18).Rio de Janeiro, Brazil：International Institute of Acoustics and Vibration，2011: 934-939.

[8]MIKOTA G. Modal analysis of hydraulic pipelines [J].Journal of Sound and Vibration,2013,332(16):3794-3805.

[9]MALEKZADEH R, HENKES R A W M, MUDDE R F. Severe slugging in a long pipeline-riser system: experiments and predictions [J]. International Journal of Multiphase Flow, 2012, 46: 9-21.

[10]GORIN S V, KUKLIN M V. Reducing low-frequency vibration in hydraulic systems by means of Helmholtz resonators[J]. Russian Engineering Research,2010, 30(5): 493-495.

[11]艾超, 孔祥东, 陈文婷, 等.液压型风力发电机组主传动系统稳速控制研究[J].太阳能学报，2014，35(9)：1757-1763.

AI Chao,KONG Xiangdong,CHEN Wenting,etal.Research on speed control of the main translation system of hydraulic wind energy conversion system[J].Acta Energiae Solaris Sinica,2014,35(9): 1757-1763.

[12]蔡毅刚. 流体传输管道动力学[M].杭州：浙江大学出版社，1989：16-19.

Resonance Analysis of a Hydraulic-driven Floor-type Wind Turbine Unit with Long Transmission Pipeline

AIChao1,2,LIUYanjiao3,YEZhuangzhuang3,KONGXiangdong1,2

(1. MOE's Key Laboratory of Advanced Forging & Stamping Technology and Science, Yanshan University, Qinhuangdao 066004, Hebei Province, China; 2. Hebei Key Laboratory of Heavy Machinery Fluid Power Transmission and Control, Yanshan University, Qinhuangdao 066004,Hebei Province, China; 3. College of Mechanical Engineering, Yanshan University,Qinhuangdao 066004, Hebei Province, China)

Abstract：To investigate the stable operation conditions of a hydraulic-driven floor-type wind turbine system with long transmission pipeline, the effects of its system parameters on the system resonance were explored, based on which a mathematical model was established for the main drive system, and subsequently the resonance excitation sources were studied from the aspects of energy input, hydraulic components and load output etc., while factors influencing the pressure ratio of the system were analyzed, thus the influence of various parameters on the system resonance were determined. Results illustrate that the parameters, such as the tube diameter, tube length and oil viscosity, have a great influence on the amplitude of pressure ratio, while the movement viscosity and volume modulus also affect the operating frequency of the system; the system resonance frequency exhibits in the form of odd multiples of the fundamental frequency.

Key words：hydraulic-driven floor-type; wind turbine unit; long transmission pipeline; resonance excitation source; pressure transmission

收稿日期：2015-08-24

修订日期：2015-10-20

基金项目：国家自然科学基金资助项目(51405423)；河北省高等学校科学技术研究青年基金资助项目(QN20132017)；燕山大学青年教师自主研究计划课题资助项目(13LGB005)

作者简介：艾超(1982-)，男，河北唐山人，副教授，博士，研究方向为液压型风力发电机组.

文章编号：1674-7607(2016)07-0556-07中图分类号：TH137； TK8

文献标志码：A学科分类号：480.60

孔祥东(通信作者)，教授，博士，电话(Tel.)：0335-8051166;E-mail：xdkong@ysu.edu.cn.