南极洲地表平均温度的定量分析

朱家明，高非含 ，陈啸远，印芷水

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)



南极洲地表平均温度的定量分析

朱家明，高非含 ，陈啸远，印芷水

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

摘要：针对如何定义并评估区域平均地表温度的问题，使用了MATLAB、EXCEL等软件，分别建立极限区域平均地表温度模型、三维插值模型和多项式拟合模型，从而得出了南极洲从2001—2015年平均地表温度值以及其与时间的函数关系式。紧接着根据得出的温度与时间的关系对未来近5年进行了预测，以便更好地掌控未来温度信息，做出及时的应对措施。

关键词：南极洲；地表平均温度；气候变暖

0引言

有专家测算南极洲近15年的平均地表温度有下降趋势的结论[1]。紧接着还对南极洲未来近5年的平均地表温度进行简单预测，以便更好地掌控未来温度信息，本文旨在寻找南极洲地表平均温度的趋势来估计全球是否变暖并建立了区域极限平均地表温度模型(详见2015年小美赛数学建模B题)。

1地表温度的评价结果

1.1研究思路

我们建立了三维插值模型对新定义的平均地表温度进行求解，得出了南极洲从2001—2015年间的平均地表温度值定义并评估平均地表温度。依据理想平均地表温度计算公式，并结合极限思想建立了连续离散化地表温度模型，对平均地表温度进行了新的定义。紧接着，我们建立了三维插值模型对新定义的平均地表温度进行求解，得出了南极洲从2001—2015年间的平均地表温度值，建模流程如图1。

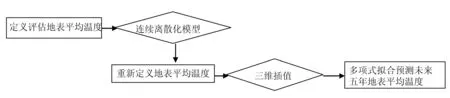
图1　求解平均地表温度思路流程图

1.2数据处理

据英国南极调查网站整理的数据，理想化的情况下可将区域地表平均温度积分并与面积作比，而在实际计算中,一定区域内的温度一般由若干个观测点得到的离散数据，不是一个连续函数, 所以我们建立连续离散化模型，通过三维插值进行求解。

为更好地对南极洲所在区域有限的考察站的温度数据进行样条插值，需要对南极洲进行直角坐标系的建立，并对各南极考察站进行坐标表示。在此过程中我们打算将球面上的南极洲视为平面。通过网络搜集南极洲的平面地图，建立平面直角坐标系，见下图2所示。

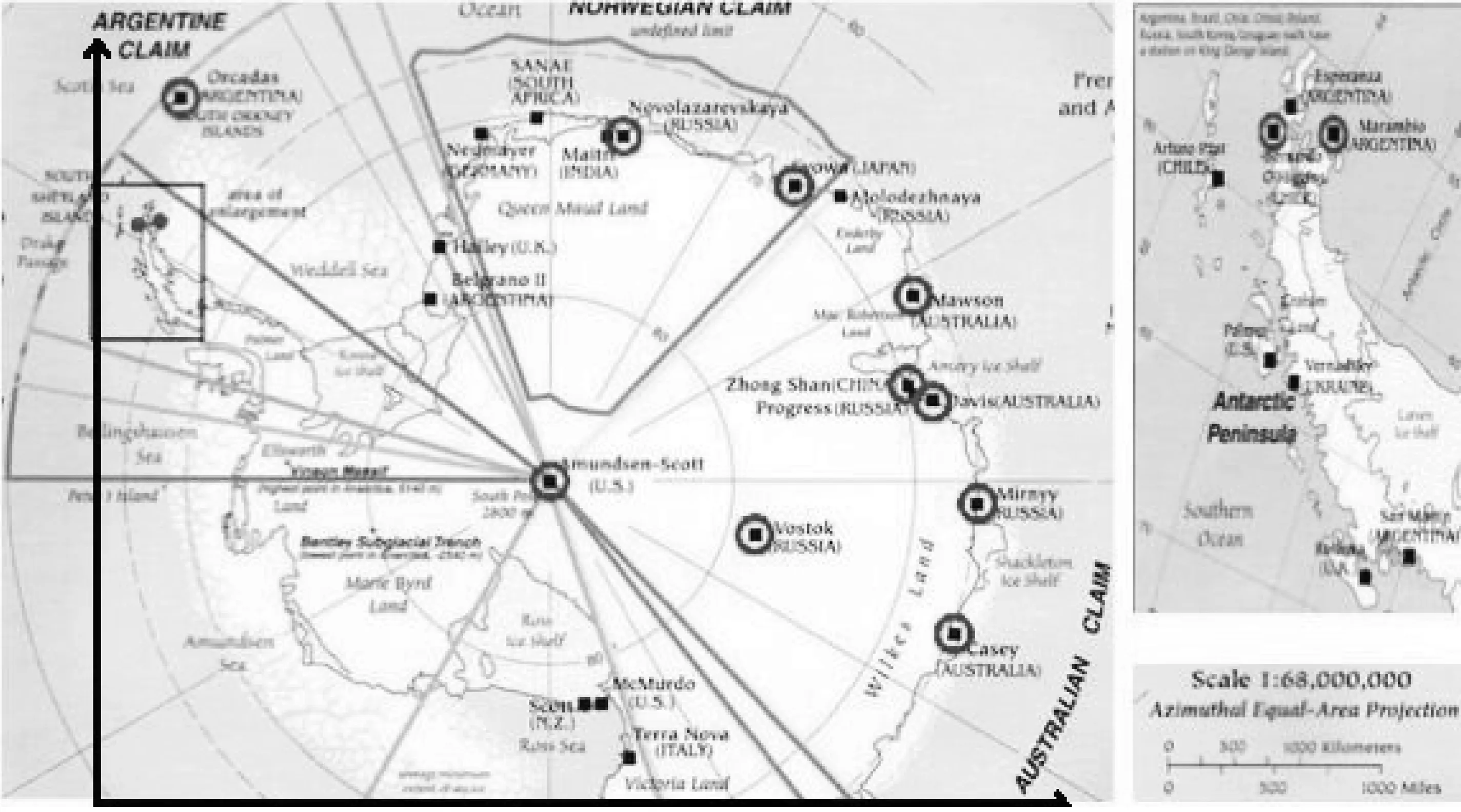
图2　南极洲考察站示意图

利用软件电子尺对图2中的各个考察站在平面直角坐标系的位置进行测量得到它们的坐标数据，并结合图中所给的比例尺进行实际距离的换算，测量结果和换算结果见下表1所示。

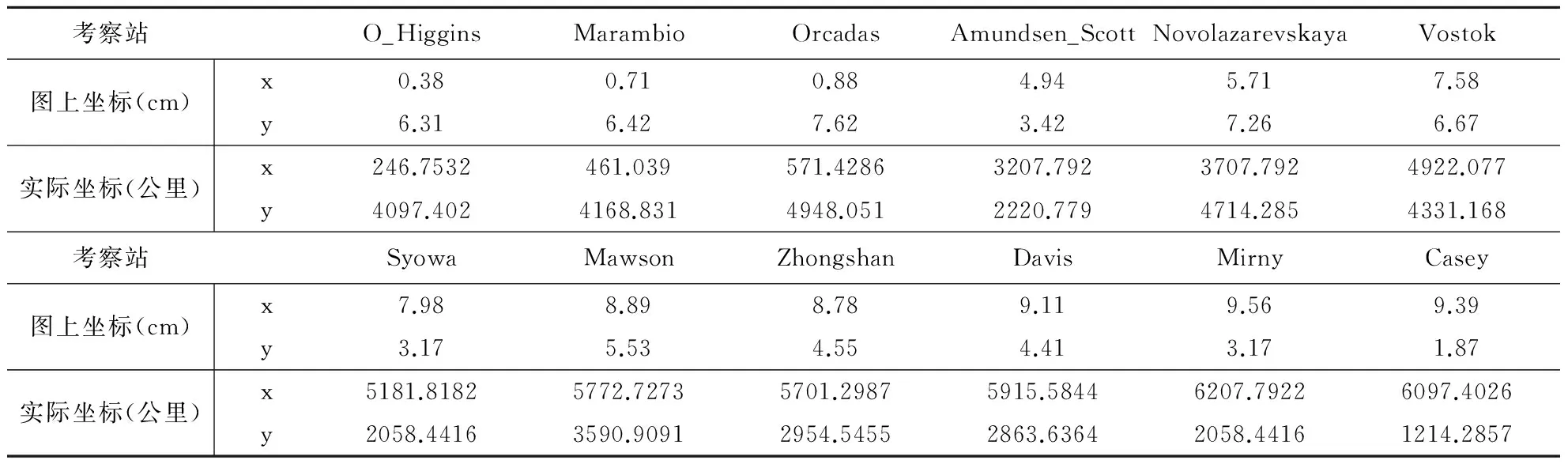
表1　考察站位置坐标数据

结合表1中的实际坐标数据，运用MATLAB软件对坐标平面内的各个考察站进行标示，标示结果见下图3所示。

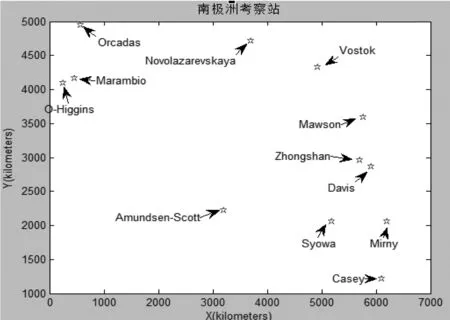
图3　各个考察站坐标标示

2极限区域地表平均温度模型

2.1研究思路

据英国南极调查网站整理的数据，理想化的情况下可将区域地表平均温度积分并与面积作比，而在实际计算中，一定区域内的温度一般是由若干个观测点得到的离散数据，不是一个连续函数, 所以我们建立极限区域平均温度模型，通过三维插值进行求解。

2.2模型建立

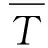
(1)

在实际计算中区域Φ内的温度一般是由若干个观测点得到的离散数据，不是一个连续函数，区域Φ的温度不能都由观测点体现，因此区域Φ内的理想平均温度不可因此求得。

对于离散的观测点数据，如果观测点的数量很多，有i个。当i趋于无穷大时，那么对Φ内的i个观测点的温度T(r，t)进行加总并与区域Φ的面积S作比值，就得到了该区域Φ的平均温度计算公式：

(2)

由于观测点i是无穷大的，可理解成区域内每个观测点所占的面积是无穷小的。设△Ti(t) 为面积大小为△的第i个观测点的温度，当面积△趋于无穷小时，将区域Φ内的i个观测点的温度进行加总并与区域Φ的面积作比值，就得到了该区域Φ的平均地表温度计算公式：

(3)

3三维插值模型

3.1研究思路

针对上述区域Φ的平均温度求解公式(3)，我们知道需要尽可能多的观测点数据，这样才能使每个观测点所占的面积尽可能地小。在现实生活中对某个区域各个观测点的数据采集量是有限的，远远无法用于公式(3)来对该地区的平均温度进行计算。现在需要通过区域内有限个观测点地表温度数据得到区域内尽可能多的地表温度数据。我们可以利用软件MATLAB对该区域已有的有限个观测点的的数据进行三维插值[3]，建立三维插值模型，进而得到该区域内足够多的数据。

3.2模型建立

通过使插值点间断尽可能小的方法进行插值，这样就能得到该区域内极小面积内所对应的地表温度值。假设有N个极小区域面积所对应的地表温度数据，记作△Ti(t)。从而就可以对这N个极小区域面积所对应的地表温度数据△Ti(t)进行加总并与区域面积作比值，这样便得到了新的区域平均温度估算公式：

(4)

公式(4)中的N是通过设置极小间断进行三维插值得到的区域观测点数量，是个很大的数量。这样在允许的误差范围内，公式(4)就能对公式(3)进行数值上的估算。

3.3模型求解结果

2001—2003年插值结果见下图4所示。

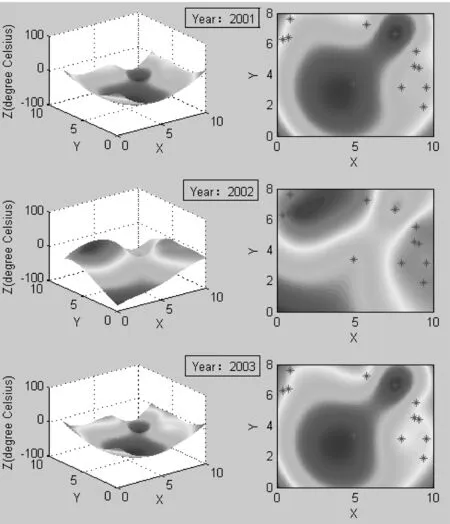
图4　2001-2003年地表平均温度插值结果

在上述图4中，左侧的三维曲面表示区域温度的起伏状况，右侧是三维地表温度的俯视图像，其中的‘*’表示南极洲上的各个考察站。在图中，冷色区域代表的地表温度要低于暖色区域所代表的地表温度，从而可以看出南极洲的平均地表温度有高有低，存在着较大的地理区域差异性。

同样，做出2004—2015年南极洲平均地表温度的三维插值图，见下图5～图8所示。

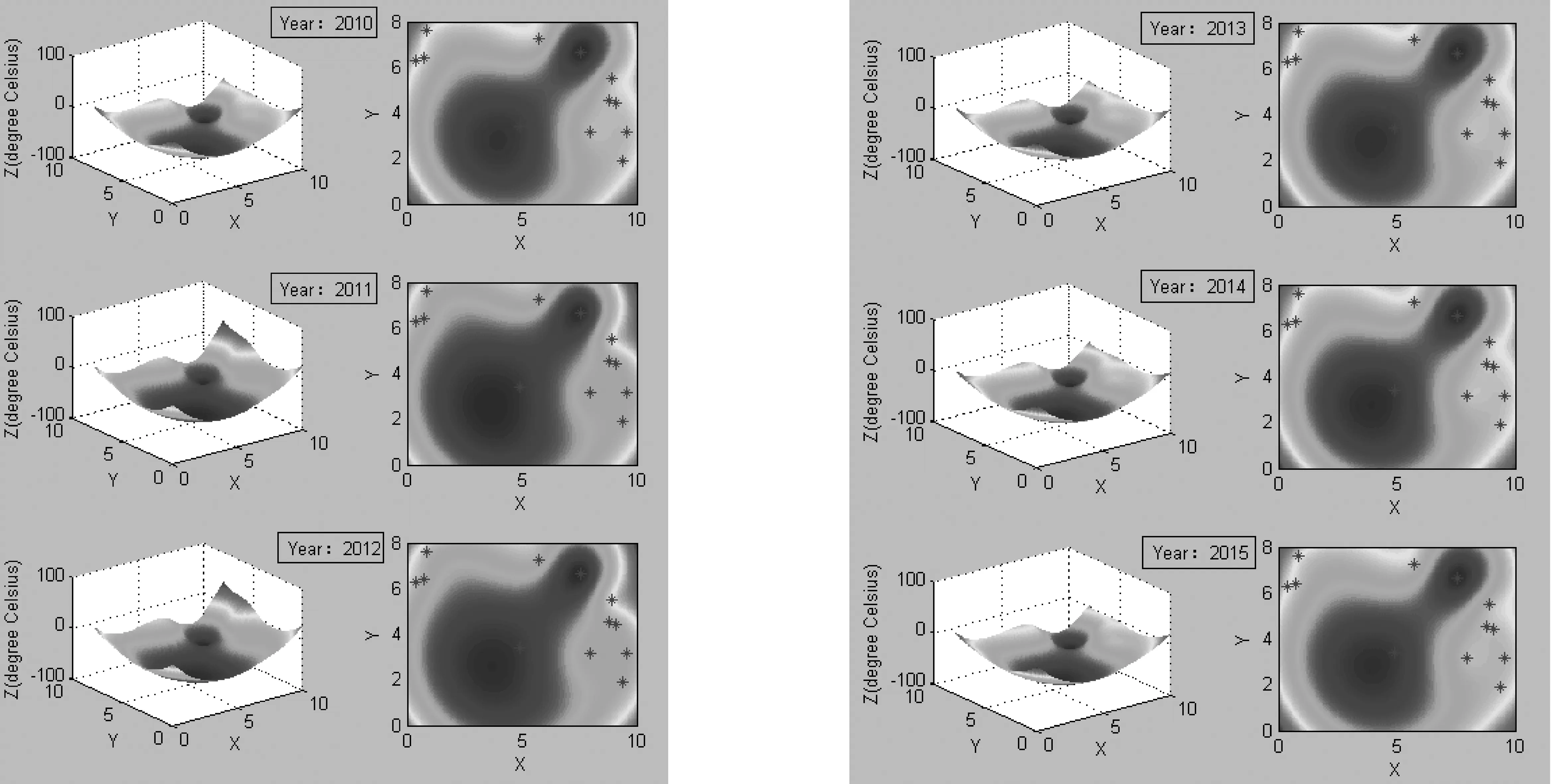
图7　2010—2012地表平均温度插值结果　　图8　2013—2015地表平均温度插值结果

4多项式拟合模型

4.1研究思路

要描述南极地区地表温度和时间之间的情况,首先需要对从2001—2015年南极地区的地表温度进行分析，找出地表温度与年份之间的关系。

运用软件MATLAB表1据进行散点图绘画，年份与平均地表温度间的散点关系见下图9所示。

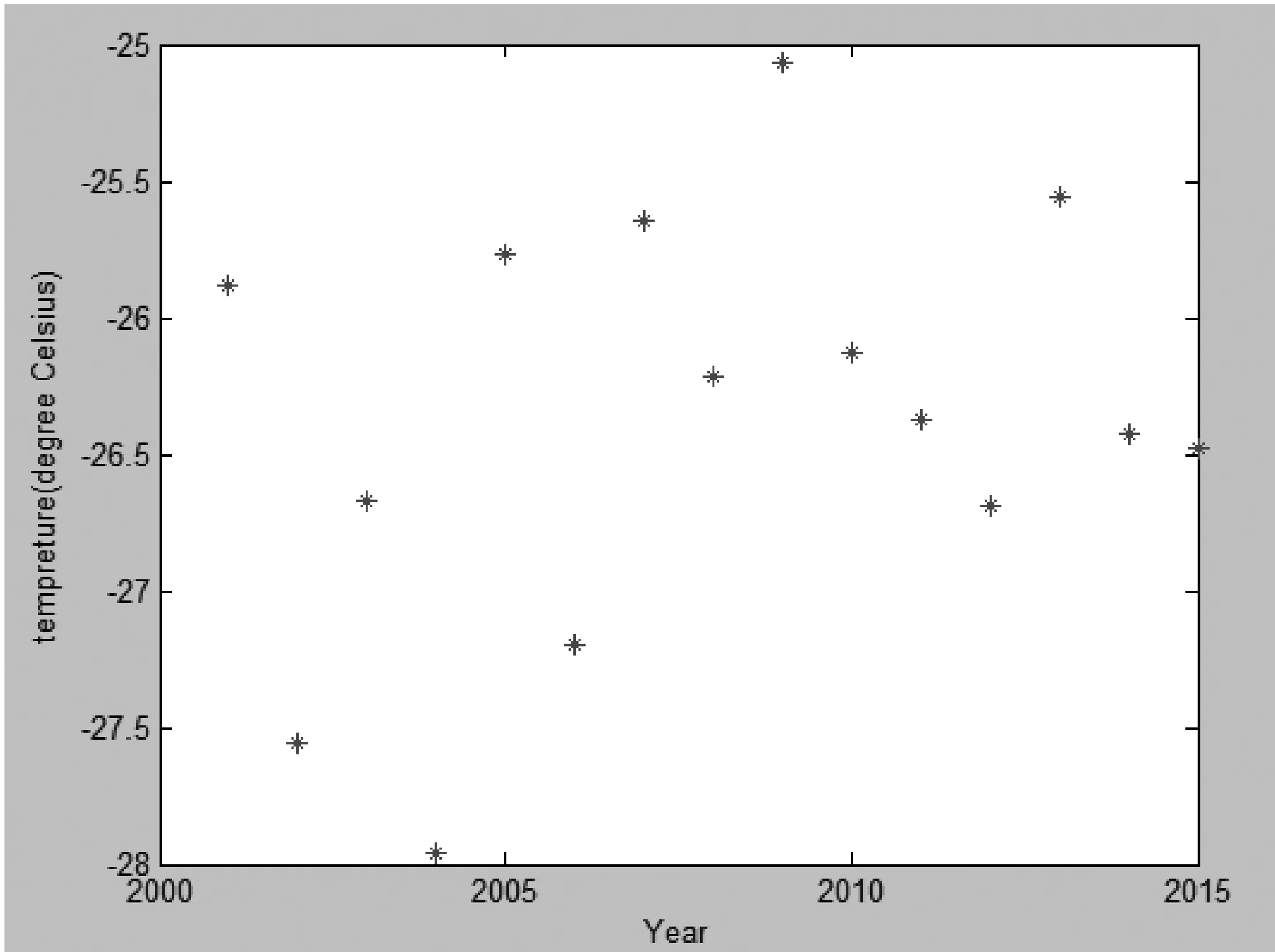
图9　年份与平均地表温度间的散点关系

通过上图发现时间与地表温度间大致呈现出多项式函数关系，所以可对散点之间进行多项式拟合。以(年份-2000)为自变量X，地表温度为因变量Y分别进行一至四次多项式拟合：

一次多项式拟合：Y1=ax+b

(5)

二次多项式拟合：Y2=a2x2+a1x+b

(6)

三次多项式拟合：Y3=a3x3+a2x2+a1x+b

(7)

四次多项式拟合：Y3=a4x4+a3x3+a2x2+a1x+b

(8)

为了能够更好地反映地表温度与时间之间的关系，应对上述多项式进行误差计算。设时间所对应的真实地表温度值为Y，根据拟合出来的多项式计算出来的地表温度值为Yi(i=1，2，3，4)。计算真实值与计算值间的离差平方和，选取离差平方和最小所对应的多项式。其中，离差平方和计算公式为：

(9)

运用软件MATLAB对表1的数据分别进行一至四次多项式拟合，拟合结果和各自的离差平方和见下表2所示。

表2　拟合结果和各自的离差平方和

由上表可以看出三次多项式和四次多项式的离差平方和都比较小，下面运用软件MATLAB画出二者和实际数据的图像，见下图10所示。

图10　拟合图

虽然四次多项式的离差平方和小于三次多项式离差平方和，但是从上述图中可以看出，四次多项式的最终趋势是上升的，在未来的近几年会达到很高的温度，这不符合南极地区未来的地表气温状况，故舍去四次多项式，最终选择三次多项式作为2001—2015年间南极地表温度和时间之间关系表达式。

y3=-0.0038x3+0.830x2-0.4120x-26.2556

(10)

通过上述公式(10)，可以简单地对南极洲未来几年的地表平均温度进行预测。取P液，可以得到未来2016年、2017年、2018年、2019年和2020年南极洲的平均地表温度。计算结果见下表3所示。

表3　2016年～2020年预测温度

表3的结果反映了南极洲未来5年的平均地表温度呈现下降的趋势，由此可以分析：全球变暖的现象日趋严重，该结论正与全球变暖引起极地冰雪融化并吸收热量，从而导致地表平均温度逐年下降的物理现象相吻合。

5结语

我们建立了三维插值模型，通过设置极小间断进行三维插值得到的区域观测点数量，是个很大的数量。这样在允许的误差范围内，进行数值上的估算。这近15年南极洲平均地表温度大致在-25摄氏度～-27摄氏度范围内，且呈现下降趋势。最后建立了多项式拟合模型，对南极洲平均地表温度和时间之间的关系进行了分析，得出未来近5年南极平均地表温度也有下降趋势的结论。

[参考文献]

[1] 杨保，史锋，Sonechkin D M,等.过去千年气候变化重建研究新进展[J].中国沙漠，2011，3(2):485-491.

[2] 张晓峒.计量经济学基础.3版[M].天津：南开大学出版社，2007.

[3] 唐国利，王邵武，闻新宇，等.全球平均温度序列的比较[J].气候变化研究进展，2011，7(2):85-89.

[4] 茆诗松，程依明，濮晓龙.概率论与数理统计教程.2版[M].北京：高等教育出版社，2011.

[责任编辑：崔海瑛]

作者简介：朱家明(1973-)，男，安徽泗县人，副教授，数学建模实验室主任，从事应用数学与数学建模研究。

基金项目：国家级大学生创新创业项目(201410378192)；国家自然科学基金项目(11301001)；安徽财经大学教研项目(acjyzd201429)。

中图分类号：O119

文献标识码：A

文章编号：2095-0063(2016)03-0009-05

收稿日期：2015-12-24

DOI 10.13356/j.cnki.jdnu.2095-0063.2016.03.003