高中数学不等式易错题型和解题技巧分析

余煌浩

南京师范大学附属中学江宁分校高三（9）班



高中数学不等式易错题型和解题技巧分析

余煌浩

南京师范大学附属中学江宁分校高三（9）班

摘 要：求解不等式解集是高中数学内容的重要组成部分，其难度比较大，我们不易理解，因而常常出现错误。本文内容解析了高中数学不等式问题中容易出错的题型，如不等式与线性规划的结合、不等式中一元高次不等式问题，并分析自己的解题方案，供同学参考。

关键词：不等式问题；易错题型；解题技巧

前言

不等式是高中数学中重点和难点，每年在考试试卷中所占比例也较大，往往结合数列以压轴题的形式出现，也是易错点之一，结合自己多年的实践经验对不等式的易错题型进行了总结并分析，并给出了一些解题技巧和思路。

例1.不等式与线性规划相结合的问题

数学考试题目中，这类题型频繁在数学考试中出现。因其考察的范围广，对我们综合运用数学知识的能力要求较高。

分析：在计算三条直线所围成的三角形区域时容易出错，该题要求我们明确三个不等式的取值范围，并画出图示。在解答该题时，应先绘制三条直线，并标示其共同包含的区域（如图1所示）：

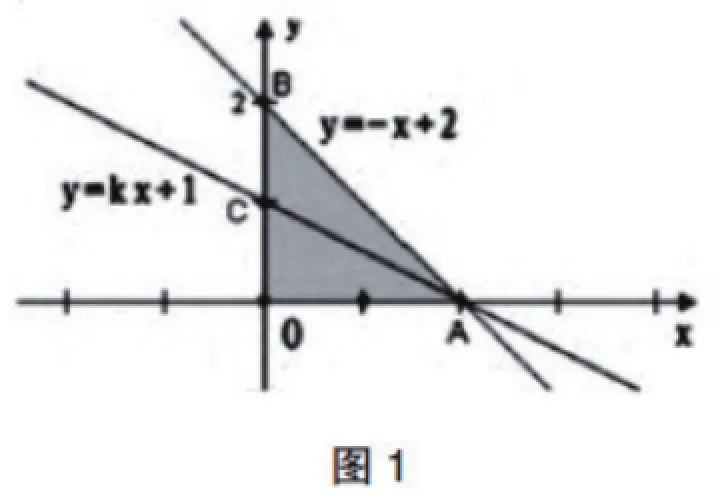
由图像可知，△ABC即为三条直线所围成的平面区域，可将题目转化为几何题目。设平面直角坐标系原点为O，将BC作为三角形的底边，AO作为三角形的高。则BC·AO=2，此时计算BO距离，即不等式y=-x+2纵轴交点与原点的距离。计算得出BO的距离等于2，同理可得CO等于1，则BC=BO-CO=2-1=1，将BO=1代入BC·AO=2，可得AO=2。即y=-x+2与y=kx+1两个方程的交点坐标为（y，2），将坐标代入两方程中，分别得到y=2k+1和y=0，将两个式子合并可得：0=2k+1，由此可得，k=-

总结：解答此类题目的技巧共有两个：第一，在求该类型问题或遇到求解极值的问题时，应先绘制出不等式组的可行域，将其转化为几何知识，理解可行域的几何意义，之后将不等式转化为等式，通过计算解决题目问题。第二，将不等式化为函数，并为函数设定一部分参考值，从函数入手，观察不同参考值下函数图形的变化，从而逐渐锁定影响函数变化的量，并对其进行求解。这两种方法是解答该类问题的主要解决方法。

例2.高次不等式问题

这类题型同样是高中考试中常出现的问题，我们在该类题型中出现错误，原因主要有三点。第一，我们忽略了题目中部分隐性的要求，如高次分式不等式中，我们会遗忘分母不能为零这一要求。第二，我们对解集的区域不明，部分我们虽然能够得出解集的范围，但对范围边界不明，主要体现于我们不能确定解集是否要取边界值。第三，在使用“穿根法”时，不能确定函数的升降规律。以上便是构成我们在解答问题时出错的原因。

题目二：求不等式（x+3）（x-2）（x-4）≤0的解集。

分析：该题已明确给出我们函数的根，分别为：x=-3、x=2、x=4。我们能够准确在序轴中标示三个零点，将序轴分为四个区间。我们运用穿根法，从最右端的零点开始，由右上方过右端零点向左下方穿过，之后依次穿过每个零点，形成一条函数曲线图（如图2所示）。

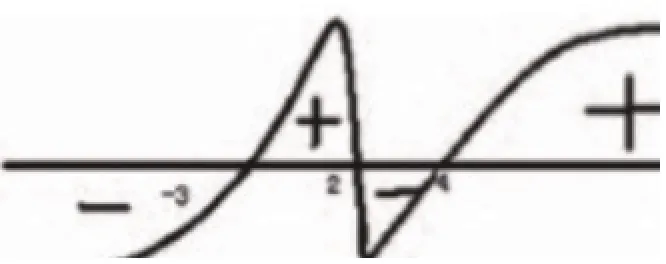
图2

之后我们按照题目要求，进行图像选择。因为题目要求整式小于0，所以我们应选择序轴以下的图像，即得出不等式的解集（-，-3）U（2，4）。我们继续分析题目，可以发现，题目中的不等符号是“≤”，因此边界值可以纳入集合当中，所以该题最终的解集为（-，-3］U［2，4］。

总结：我们在解决该类问题时，应熟练掌握穿根法这一解题方式，运用穿根法能够提高我们的解题速度，降低题目难度。同时我们解得解集后，也应对解集的临界点进行判定，确定其是否可以纳入解集范围内，从而使解集不会出现问题。

例3.含参不等式问题

往往需要对参数进行分类讨论，选择合理的分类依据进行完成（参数是否为零等，不重不漏）。

题目三：解关于x的不等式ax2－2x+1＞0（a为常数，a∈R）。

分析：此题要分情况来讨论，分别是a=0、a＞0 和a＜0三种情况，同时在a＞0时还要区分判别式△的值。此类题型的解题技巧是要牢记参数要对参数进行分类来说明，保证不重不漏。基本不等式：凑项，拆项，配系数，换元，取倒数，“1”的代换。

例4.解绝对值不等式

解绝对值不等式主要通过同解变形去掉绝对值符合转化为一元一次或一元二次不等式（组）进行求解，含有多个绝对值符合的不等式，一般可用零点分段法求解，但利用实数绝对值得几何意义求解较便捷，对于最值问题也可以考虑绝对值三角不等式。核心思想是“想方设法”将其转换成不含绝对值的式子求解。

例5.不等式恒成立问题

不等式恒成立问题往往与数列或抽象函数相结合来命题，这类问题是高中不等式问题的难点，而且由于抽象性较强，极易出错。

题目四：设函数f（x）=ln（1+x），g（x）=xf`（x），x≥0，其中f`（x）是f（x）的导函数。

（Ⅰ）令 g1（ x）= g（ x），求gn（x）的表达式；

（Ⅱ）若f（x）≥ag（x）恒成立，求实数a的取值范围；

（Ⅲ）设n∈N+，比较g（1）+g（2）+…+g（n）与nf（n）的大小，并加以证明。

分析：该题的考点是结合不等式、函数导数求闭区间上函数的最值并研究函数的单调性。

解答此类题型的技术往往采取分离变量或适当变形，或变换主元，或构造函数，再利用函数的单调性或基本不等式进行求解；最值问题常常转化成利用基本不等式求解。同时在转化不等式中要注意不等式不等号的方向，注意“一正，二定，三相等”。